Xây dựng các tình huống dạy học hỗ trợ quá trình toán học hóa

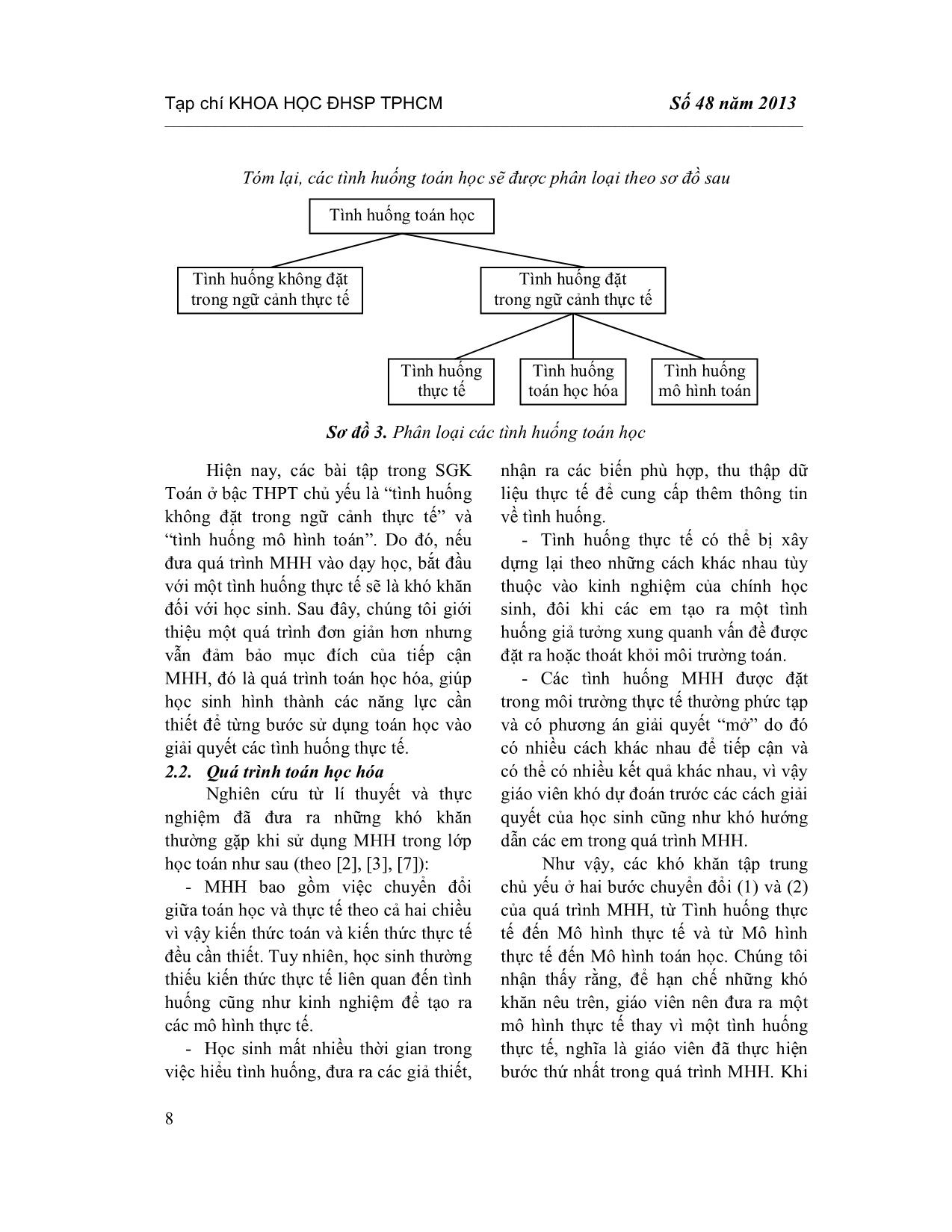
Tạp chí KHOA HỌC ĐHSP TPHCM Nguyễn Thị Tân An 
_____________________________________________________________________________________________________________ 
 5 
XÂY DỰNG CÁC TÌNH HUỐNG DẠY HỌC 
HỖ TRỢ QUÁ TRÌNH TOÁN HỌC HÓA 
NGUYỄN THỊ TÂN AN* 
TÓM TẮT 
Theo Kaiser [5], việc dạy toán nên quan tâm đến những ví dụ xuất phát từ thực tế 
giúp học sinh thấy được mối quan hệ giữa toán học và cuộc sống cũng như đạt được 
những năng lực cho phép giải quyết các vấn đề thực tế bằng công cụ toán học. Trong bài 
báo này, chúng tôi giới thiệu quá trình toán học hóa cùng với các gợi ý xây dựng tình 
huống dạy học hỗ trợ quá trình này, đồng thời trình bày cách phân loại các tình huống 
toán học giúp cho việc sử dụng các tình huống vào dạy học thuận lợi và đúng mục đích 
hơn. 
Từ khóa: mô hình hóa toán học, quá trình toán học hóa, tình huống toán học hóa. 
ABSTRACT 
Building teaching situations to assist the mathematisation process 
According to Kaiser, teaching mathematics should pay attention to reality-based 
examples helping students understand the relationship between mathematics and everyday 
life, as well as achieve the competence that enables them to solve real life problems with 
mathematical tools [5]. In this article, we introduce the mathematisation process together 
with some suggestions to build teaching situations assisting this process, and present how 
to classify mathematical situations, which makes the use of situations in teaching more 
convenient and closer to the targets. 
Keywords: mathematisation process, mathematisation situation. 
1. Giới thiệu 
Mô hình hóa toán học (MHH) trong 
giáo dục chính thức xuất hiện đầu tiên tại 
hội nghị của Freudenthal năm 1968. 
Nhưng một dấu mốc quan trọng của việc 
giới thiệu MHH vào nhà trường là nghiên 
cứu của Pollak năm 1979, theo ông giáo 
dục toán phải có trách nhiệm dạy cho học 
sinh cách sử dụng toán trong cuộc sống 
hàng ngày (Dẫn theo [1]). Từ đó, dạy và 
học MHH trong nhà trường trở thành một 
chủ đề nổi bật trên phạm vi toàn cầu. Ví dụ: 
- Nghiên cứu của PISA (Programme 
for International Student Assessment) 
* NCS, Trường Đại học Sư phạm TPHCM 
nhấn mạnh mục đích của giáo dục toán là 
phát triển khả năng học sinh sử dụng toán 
vào cuộc sống hiện tại và tương lai. 
- Hội nghị quốc tế về dạy mô hình 
hóa và áp dụng toán ICTMA 
(International Conferences on the 
Teaching of Mathematical Modelling and 
Applications) tổ chức hai năm một lần 
với mục đích thúc đẩy ứng dụng và MHH 
ở tất cả các lĩnh vực của giáo dục toán. 
Trong hội nghị quốc tế về dạy học 
toán ICMI 14, Blum nhận xét [1]: Mặc dù 
đã có nhiều tài liệu, nghiên cứu đề cập đến 
MHH trong giáo dục toán nhưng vai trò 
của MHH vẫn ít thể hiện ở tất cả các cấp 
học. Làm thế nào để tích hợp MHH vào 
Tạp chí KHOA HỌC ĐHSP TPHCM Số 48 năm 2013 
_____________________________________________________________________________________________________________ 
 6 
dạy học toán được thực hiện dễ dàng hơn? 
Trên cơ sở phân tích quá trình 
MHH và những khó khăn khi sử dụng 
MHH trong lớp học, bài báo đề xuất một 
hướng giải quyết đối với câu hỏi trên, đó 
là thay thế các tình huống thực tế bằng 
các tình huống toán học hóa, lúc này học 
sinh sẽ thực hiện một quá trình con của 
quá trình MHH - quá trình toán học hóa. 
Bài báo cũng đưa ra những gợi ý giúp 
giáo viên có thể xây dựng các tình huống 
dạy học hỗ trợ quá trình toán học hóa 
này, đồng thời trình bày cách phân loại 
tình huống toán học cùng với bốn ví dụ 
minh họa giúp việc sử dụng các tình 
huống vào dạy học thuận lợi hơn và đúng 
mục đích hơn. 
2. Nội dung 
2.1. Quá trình mô hình hóa toán học 
Mô hình hóa toán học là thuật ngữ 
được sử dụng để chỉ quá trình giải quyết 
những vấn đề thực tế bằng công cụ toán 
học [1]. MHH cho phép học sinh kết nối 
toán học nhà trường với thế giới thực, chỉ 
ra khả năng áp dụng các ý tưởng toán, 
đồng thời cung cấp một bức tranh rộng 
hơn, phong phú hơn về toán học, giúp 
việc học toán trở nên ý nghĩa hơn. 
Khái niệm mô hình hóa trong dạy 
học toán thường được sử dụng theo hai 
mục đích: 
- Mô hình hóa để học toán: MHH là 
một phương tiện hỗ trợ việc học các khái 
niệm và quá trình toán học của học sinh, 
chẳng hạn như tạo động cơ giúp hình 
thành và hiểu một khái niệm hoặc minh 
họa các nội dung toán học trừu tượng, 
phức tạp. 
- Học toán để mô hình hóa: MHH là 
một mục đích của việc học toán, nhằm 
trang bị cho học sinh các năng lực để có 
thể sử dụng toán trong nhiều ngữ cảnh và 
tình huống bên ngoài lớp học. 
Ở bài báo này chúng tôi quan tâm 
đến MHH theo phương diện thứ hai, phát 
triển khả năng sử dụng toán của học sinh 
trong cuộc sống hiện tại và tương lai. 
Nhiều sơ đồ đã được sử dụng để 
mô tả quá trình MHH, như của Pollak, 
Blum, Kaiser [4] hay Stillman & 
Galbraith [7], đó là một quá trình lặp 
gồm nhiều bước, bắt đầu với một tình 
huống thực tế và kết thúc là một phương 
án giải quyết thành công ha ... o sơ đồ sau 
Sơ đồ 3. Phân loại các tình huống toán học 
Hiện nay, các bài tập trong SGK 
Toán ở bậc THPT chủ yếu là “tình huống 
không đặt trong ngữ cảnh thực tế” và 
“tình huống mô hình toán”. Do đó, nếu 
đưa quá trình MHH vào dạy học, bắt đầu 
với một tình huống thực tế sẽ là khó khăn 
đối với học sinh. Sau đây, chúng tôi giới 
thiệu một quá trình đơn giản hơn nhưng 
vẫn đảm bảo mục đích của tiếp cận 
MHH, đó là quá trình toán học hóa, giúp 
học sinh hình thành các năng lực cần 
thiết để từng bước sử dụng toán học vào 
giải quyết các tình huống thực tế. 
2.2. Quá trình toán học hóa 
Nghiên cứu từ lí thuyết và thực 
nghiệm đã đưa ra những khó khăn 
thường gặp khi sử dụng MHH trong lớp 
học toán như sau (theo [2], [3], [7]): 
- MHH bao gồm việc chuyển đổi 
giữa toán học và thực tế theo cả hai chiều 
vì vậy kiến thức toán và kiến thức thực tế 
đều cần thiết. Tuy nhiên, học sinh thường 
thiếu kiến thức thực tế liên quan đến tình 
huống cũng như kinh nghiệm để tạo ra 
các mô hình thực tế. 
- Học sinh mất nhiều thời gian trong 
việc hiểu tình huống, đưa ra các giả thiết, 
nhận ra các biến phù hợp, thu thập dữ 
liệu thực tế để cung cấp thêm thông tin 
về tình huống. 
- Tình huống thực tế có thể bị xây 
dựng lại theo những cách khác nhau tùy 
thuộc vào kinh nghiệm của chính học 
sinh, đôi khi các em tạo ra một tình 
huống giả tưởng xung quanh vấn đề được 
đặt ra hoặc thoát khỏi môi trường toán. 
- Các tình huống MHH được đặt 
trong môi trường thực tế thường phức tạp 
và có phương án giải quyết “mở” do đó 
có nhiều cách khác nhau để tiếp cận và 
có thể có nhiều kết quả khác nhau, vì vậy 
giáo viên khó dự đoán trước các cách giải 
quyết của học sinh cũng như khó hướng 
dẫn các em trong quá trình MHH. 
Như vậy, các khó khăn tập trung 
chủ yếu ở hai bước chuyển đổi (1) và (2) 
của quá trình MHH, từ Tình huống thực 
tế đến Mô hình thực tế và từ Mô hình 
thực tế đến Mô hình toán học. Chúng tôi 
nhận thấy rằng, để hạn chế những khó 
khăn nêu trên, giáo viên nên đưa ra một 
mô hình thực tế thay vì một tình huống 
thực tế, nghĩa là giáo viên đã thực hiện 
bước thứ nhất trong quá trình MHH. Khi 
Tình huống toán học 
Tình huống không đặt 
trong ngữ cảnh thực tế 
Tình huống 
thực tế 
Tình huống đặt 
trong ngữ cảnh thực tế 
Tình huống 
toán học hóa 
Tình huống 
mô hình toán 
Tạp chí KHOA HỌC ĐHSP TPHCM Nguyễn Thị Tân An 
_____________________________________________________________________________________________________________ 
 9 
đó, tình huống đưa ra vẫn được đặt trong 
môi trường thực tế, học sinh vẫn phải 
chuyển đổi tình huống từ thực tế vào môi 
trường toán, giải quyết vấn đề toán học, 
đưa ra kết quả toán và giải thích kết quả 
đó trong ngữ cảnh thực tế ban đầu. Quá 
trình này gọi là quá trình toán học hóa. 
Rõ ràng cách làm như vậy vẫn đảm bảo 
mục đích của tiếp cận MHH theo 
Stillman [8]: 
- Phát triển khả năng áp dụng toán 
vào những vấn đề thực tế; 
- Đưa toán học ra khỏi phạm vi lớp 
học; 
- Sử dụng ngữ cảnh thực tế là một 
thành phần then chốt trong quá trình 
MHH; 
- Thực hiện chuyển đổi từ môi trường 
thực tế sang môi trường toán và ngược 
lại.
Sơ đồ 4. Quá trình toán học hóa 
So với tình huống thực tế ban đầu, 
tình huống toán học hóa giúp học sinh 
hình dung rõ hơn về tình huống, có thêm 
dữ liệu thông tin; vì vậy, quá trình xây 
dựng mô hình toán học diễn ra thuận lợi 
hơn. 
Quá trình toán học hóa cũng được 
xem là một cơ sở lí thuyết quan trọng của 
chương trình đánh giá PISA [6], tuy 
nhiên quá trình đó không xuất phát với 
một tình huống toán học hóa mà bắt đầu 
với một tình huống đặt trong ngữ cảnh 
thực tế và gồm 5 bước chia thành 3 quá 
trình nhỏ: (1) xây dựng tình huống một 
cách toán học; (2) sử dụng các khái niệm, 
quá trình, suy luận toán học; (3) giải 
thích, áp dụng và đánh giá kết quả. Mỗi 
câu hỏi trong các tình huống của PISA 
chỉ đánh giá một trong ba quá trình này. 
Do đó, quá trình toán học hóa chúng tôi 
đưa ra trong bài báo không dựa vào quá 
trình toán học hóa của PISA mà xuất phát 
từ quá trình MHH được trình bày ở mục 
2.1. 
Trên cơ sở mô tả bước 1 của quá 
trình MHH, giáo viên có thể xây dựng 
các tình huống dạy học hỗ trợ quá trình 
toán học hóa ở sơ đồ 4: 
- Bắt đầu với một tình huống thực tế, 
tình huống đó phải thích hợp với đối 
tượng học sinh và chứa đựng nội dung 
toán các em đã học. 
- Dự kiến những kiến thức, kĩ năng 
toán học mà học sinh cần sử dụng để 
thiết lập mô hình toán và giải toán; 
- Làm cho tình huống rõ ràng hơn; 
Kết quả 
thực tế 
Kết quả 
toán học 
Tình huống 
toán học hóa 
Mô hình 
toán học 
(1) 
(2) 
(3) 
(4) 
Tạp chí KHOA HỌC ĐHSP TPHCM Số 48 năm 2013 
_____________________________________________________________________________________________________________ 
 10 
Tạo mối liên kết giữa tình huống thực tế 
và toán học bằng cách: 
o Thực hiện lí tưởng hóa, đơn 
giản hóa, đặc biệt hóa vấn đề; 
o Đưa ra các giả thiết phù hợp; 
o Nhận ra các biến trong tình 
huống để biểu diễn các đặc điểm cần 
thiết; 
o Thu thập dữ liệu thực tế để 
cung cấp thêm thông tin cho tình huống; 
o Mô tả chi tiết tình huống; 
o Câu hỏi được đặt ra một cách 
rõ ràng. 
- Tình huống toán học hóa vẫn phải 
đảm bảo ngữ cảnh bao gồm các đối tượng 
thực. 
Ngoài ra, để tạo được những tình 
huống THH có ý nghĩa và phù hợp với 
học sinh, giáo viên có thể điều chỉnh các 
bài toán thực tế từ sách giáo khoa hoặc từ 
các nguồn có sẵn như các nhiệm vụ của 
PISA theo những gợi ý trên. 
2.3. Ví dụ minh họa 
Sau đây, chúng tôi minh họa một 
tình huống toán học hóa đã được chuyển 
đổi từ tình huống thực tế theo các gợi ý ở 
trên cùng với kết quả khảo sát hai nhóm 
học sinh lớp 12, gồm 92 em, khi giải 
quyết hai tình huống này. Bên cạnh đó, 
chúng tôi cũng giới thiệu thêm một tình 
huống toán học hóa, một tình huống mô 
hình toán cùng xuất phát từ tình huống 
thực tế ban đầu. 
Tình huống thực tế: Trong cuộc 
thi những người pha chế cocktail giỏi, 
ban tổ chức chuẩn bị các li thủy tinh có 
dạng như hình vẽ. Thí sinh được yêu cầu 
pha nửa li cocktail loại Martini rồi trang 
trí. Nếu em là thí sinh dự thi, em sẽ làm 
như thế nào, tại sao? (Sử dụng kiến thức 
toán để giải quyết) 
Hình 1. Li cocktail thủy tinh 
Tình huống trên được đặt ra cho 46 
học sinh lớp 12 giải quyết, những học 
sinh này đã học xong phần “thể tích của 
hình nón” vì vậy có thể sử dụng kiến thức 
đó vào tình huống. Kết quả thực nghiệm 
cho thấy tình huống khó đối với hầu hết 
học sinh mà chúng tôi khảo sát (xem 
bảng 1), bởi vì học sinh không hiểu yêu 
cầu của tình huống, không thấy được mối 
liên hệ giữa thực tế và toán học, chưa 
quen với những tình huống như vậy, hoặc 
giải quyết mà không sử dụng kiến thức 
toán, chẳng hạn: rót rượu vào 1/2 chiều 
cao của thân li, sử dụng dụng cụ có vạch 
ml, ước lượng bằng mắt, đổ li đựng đầy 
rượu qua một li khác đến khi hai li ngang 
nhau, úp ngược li. 
Bảng 1. Kết quả thực nghiệm tình huống thực tế 
Không làm Không sử dụng kiến thức toán để giải quyết 
Sử dụng kiến thức 
toán để giải quyết 
Tổng 
(học sinh) 
5 33 8 (2 HS giải đúng) 46 
Tạp chí KHOA HỌC ĐHSP TPHCM Nguyễn Thị Tân An 
_____________________________________________________________________________________________________________ 
 11 
Chỉ có 4,3% học sinh tham gia khảo 
sát đã sử dụng kiến thức toán để đưa ra 
lời giải đúng cho tình huống. Nhằm giảm 
bớt những khó khăn trên, từ tình huống 
thực tế, giáo viên có thể xây dựng tình 
huống toán học hóa, với dự kiến những 
kiến thức, kĩ năng toán học mà học sinh 
cần sử dụng là thể tích hình nón: 
- Lí tưởng hóa: li cocktail thủy tinh 
có dạng hình nón; 
- Đơn giản hóa: đưa ra hai phương án 
để học sinh lựa chọn rót 2/3 li và phụ 
thuộc vào kích thước của miệng li; 
- Cung cấp dữ liệu, thông tin: cung 
cấp thêm hình ảnh của 2 dạng li hình nón 
khác; 
- Mô tả tình huống một cách chi tiết. 
Tình huống toán học hóa 1: 
Trong cuộc thi những người pha chế 
cocktail giỏi, ban tổ chức chuẩn bị các 
li thủy tinh có dạng hình nón như hình 
vẽ. Thí sinh được yêu cầu pha nửa li 
cocktail loại Martini rồi trang trí. Bình 
là một thí sinh cho rằng cần rót 
cocktail vào 2/3 li. Nhật cho rằng cách 
của Bình không đúng vì còn tùy thuộc 
vào kích thước của miệng li. Theo em, 
ai đúng, tại sao? 
Hình 2. Các li thủy tinh với kích thước khác nhau 
Quá trình chuyển đổi từ mô hình 
thực tế sang mô hình toán, học sinh có 
thể đưa về bài toán: tìm mối liên hệ giữa 
đường cao H và h của hai hình nón, thân 
li cocktail và phần rượu bên trong li, có 
bán kính tương ứng là R, r, biết tỉ lệ thể 
tích V:v = 2:1 
Khi đó: 2
1
3
V R H và 21
3
v r h 
2 3V R H H
v r h h
Suy ra 0.79h H . 
Vậy câu trả lời là cả Nhật và Bình 
đều không đúng. 
Hình 3. Mô hình toán học của tình huống 
Tạp chí KHOA HỌC ĐHSP TPHCM Số 48 năm 2013 
_____________________________________________________________________________________________________________ 
 12 
 Thực hiện khảo sát trên 46 học sinh lớp 12 khác, chúng tôi thu được kết quả: 
Bảng 2. Kết quả thực nghiệm tình huống toán học hóa 1 
Không 
làm 
Làm không 
đúng 
Giải thích đúng 
1 trường hợp 
(Bình sai) 
Giải thích 
đúng cả 2 trường hợp 
Tổng 
(học sinh) 
0 29 10 7 (4 HS đưa ra cách rót đúng) 46 
So với tình huống thực tế, kết quả 
thu được từ tình huống toán học hóa 1 có 
một sự khác biệt lớn. Tất cả học sinh đều 
sử dụng công thức thể tích hình nón khi 
giải quyết tình huống, không có em nào 
không làm. Hầu hết các em đều xác định 
được những yếu tố toán học từ tình 
huống như v = V/2, h = 2H/3, trong đó 17 
em xác định được tỉ lệ r : R = h : H. Điều 
đó chứng tỏ học sinh hiểu được yêu cầu 
đặt ra, cũng như tìm thấy kiến thức toán 
cần áp dụng. 
Ngoài ra, như chúng tôi có đề cập ở 
phần 2.1, từ một tình huống thực tế 
chúng ta có thể tạo ra nhiều tình huống 
toán học hóa khác nhau, tùy thuộc vào 
lượng thông tin được cung cấp. Dưới đây 
là một tình huống toán học hóa khác, với 
độ khó thấp hơn tình huống 1, vì thông 
tin đã được hạn chế nhiều hơn (một loại 
li), cụ thể hơn (cho thể tích và đường 
kính), yêu cầu đặt ra đơn giản hơn. 
Tình huống toán học hóa 2: Trong 
cuộc thi những người pha chế cocktail 
giỏi, ban tổ chức chuẩn bị một loại li thủy 
tinh có dạng hình nón với dung tích chứa 
là 160 ml và đường kính miệng li là 
10cm. Thí sinh được yêu cầu pha nửa li 
cocktail loại Martini rồi trang trí. Nếu em 
là thí sinh, em sẽ rót cocktail vào li theo 
tỉ lệ nào so với chiều cao của thân li? 
Giải thích. 
A. 1/2 B. 2/3 C. 3/4 D. 4/5 
Hình 4. Phần thân li với đường kính 
và dung tích cho trước 
So với các tình huống trên, tình 
huống dưới đây cũng được đặt trong một 
ngữ cảnh thực tế, nhưng đã xác định các 
đối tượng toán học (chiều cao, thể tích), 
và yêu cầu đặt ra cho học sinh là tìm mối 
quan hệ giữa các đối tượng đó. Vì vậy, 
tình huống không phải là một tình huống 
thực tế hay là tình huống toán học hóa. 
Tình huống mô hình toán: Trong 
cuộc thi những người pha chế cocktail 
giỏi, ban tổ chức chuẩn bị một loại li thủy 
tinh có dạng hình nón như hình vẽ. Thí 
sinh được yêu cầu pha nửa li cocktail loại 
Martini rồi trang trí. Gọi H là chiều cao 
của thân li và V là thể tích của li. Hãy xác 
định chiều cao của lượng cocktail đổ vào 
theo H để thể tích cocktail trong li bằng 
V/2. 
Tạp chí KHOA HỌC ĐHSP TPHCM Nguyễn Thị Tân An 
_____________________________________________________________________________________________________________ 
 13 
Hình 5. Phần thân li với chiều cao H 
và thể tích V 
Bốn tình huống trên đều có cùng 
nội dung toán, nhưng được thiết kế với 
mức độ phức tạp giảm dần, phụ thuộc 
vào các thông tin được cung cấp, cũng 
như loại câu hỏi đặt ra. Hiện nay, học 
sinh chỉ mới gặp một số tình huống mô 
hình toán, thỉnh thoảng xuất hiện trong 
SGK. Để có thể hướng đến việc sử dụng 
kiến thức, kĩ năng toán vào giải quyết các 
tình huống thực tế, học sinh cần được 
tiếp xúc nhiều hơn với tình huống mô 
hình toán và có cơ hội làm quen các tình 
huống toán học hóa, từ mức độ đơn giản 
đến phức tạp. 
3. Kết luận 
Dạy học MHH đã và đang thu hút 
nhiều quan tâm nghiên cứu, thực hiện ở 
nhiều nước trên thế giới như Mĩ, Úc, 
Đức, Hà Lan, Singapore Qua phân tích 
các tài liệu, bài báo đưa ra một số khó 
khăn khi sử dụng quá trình MHH vào dạy 
học toán. Ngoài ra, với một khảo sát nhỏ 
trên đối tượng học sinh lớp 12, chúng tôi 
nhận thấy các em gặp nhiều khó khăn 
hơn khi giải quyết một tình huống thực tế 
so với một tình huống toán học hóa. Bên 
cạnh đó, hầu hết các bài tập “thực tế” 
trong sách giáo khoa chỉ mới dừng lại ở 
mức độ “tình huống mô hình toán”. Vì 
vậy, đối với học sinh hiện nay, khi các 
em chưa được làm quen với quá trình 
MHH toán học thì quá trình toán học hóa 
là một lựa chọn giúp học sinh hình thành 
các năng lực cần thiết để từng bước sử 
dụng toán học vào các tình huống thực tế. 
Ghi chú: Bài báo này được tài trợ một phần bởi Quỹ Phát triển Khoa học và Công 
nghệ Quốc gia Việt Nam - NAFOSTED với đề tài Mã số: VI2.2-2010.11. 
TÀI LIỆU THAM KHẢO 
1. Blum W. (2002), “ICMI Study 14: Applications and modelling in mathematics 
education – Discussion document”, ZDM, 34(5), pp. 229-239. 
2. Blum W. (2011), “Can Modelling Be Taught and Learnt? Some Answers from 
Empirical Research”, Trends in Teaching and Learning of Mathematical Modelling, 
pp. 15-27. 
3. Busse, A. & Kaiser, G. (2003), “Context in application and modelling - an empirical 
approach”, In Q. Ye, W. Blum, S.K., Houston, Q. Jiang (Eds.), Mathematical 
modelling in education and culture: ICTMA 10 (pp. 3-15), Chichester, UK: Horwood 
Publishing. 
4. Ferri, R. B. (2006), “Theoretical and empirical differentiations of phases in the 
modelling process”, ZDM, 38(2), pp. 86-95. 
(Xem tiếp trang 42) 
Tạp chí KHOA HỌC ĐHSP TPHCM Số 48 năm 2013 
_____________________________________________________________________________________________________________ 
 14 
5. Kaiser G. (2010), “Theoretical Approaches and Examples for Modelling in 
Mathematics Education”, Mathematical Applications and Modelling: Yearbook 
2010. World Scientific, pp. 219-237. 
6. OECD (2003), The PISA 2003 Assessment Framework - Mathematics, Reading, 
Science and Problem Solving Knowledge and Skills, Paris: OECD Publications. 
7. Stillman, G. & Galbraith, P. (2006), “A framework for identifying student blockages 
during transitions in the modelling process”, ZDM, 38(2), pp. 143-162. 
8. Stillman, G. (2008), “Connected Mathematics Through Mathematical Modelling and 
Applications”, In Connected maths, Proceedings of the 45th Annual Conference of 
the Mathematical Association of Victoria, eds. J. Vincent, J. Dowsey & R. Pierce, 
MAV, Melbourne: pp. 325-339. 
(Ngày Tòa soạn nhận được bài: 21-3-2013; ngày phản biện đánh giá: 14-5-2013; 
ngày chấp nhận đăng: -2013)