Xác định hàm thế năng của mô hình vỏ-lõi cho vật liệu sắt điện PbTiO₃ và ứng dụng trong tính toán độ phân cực

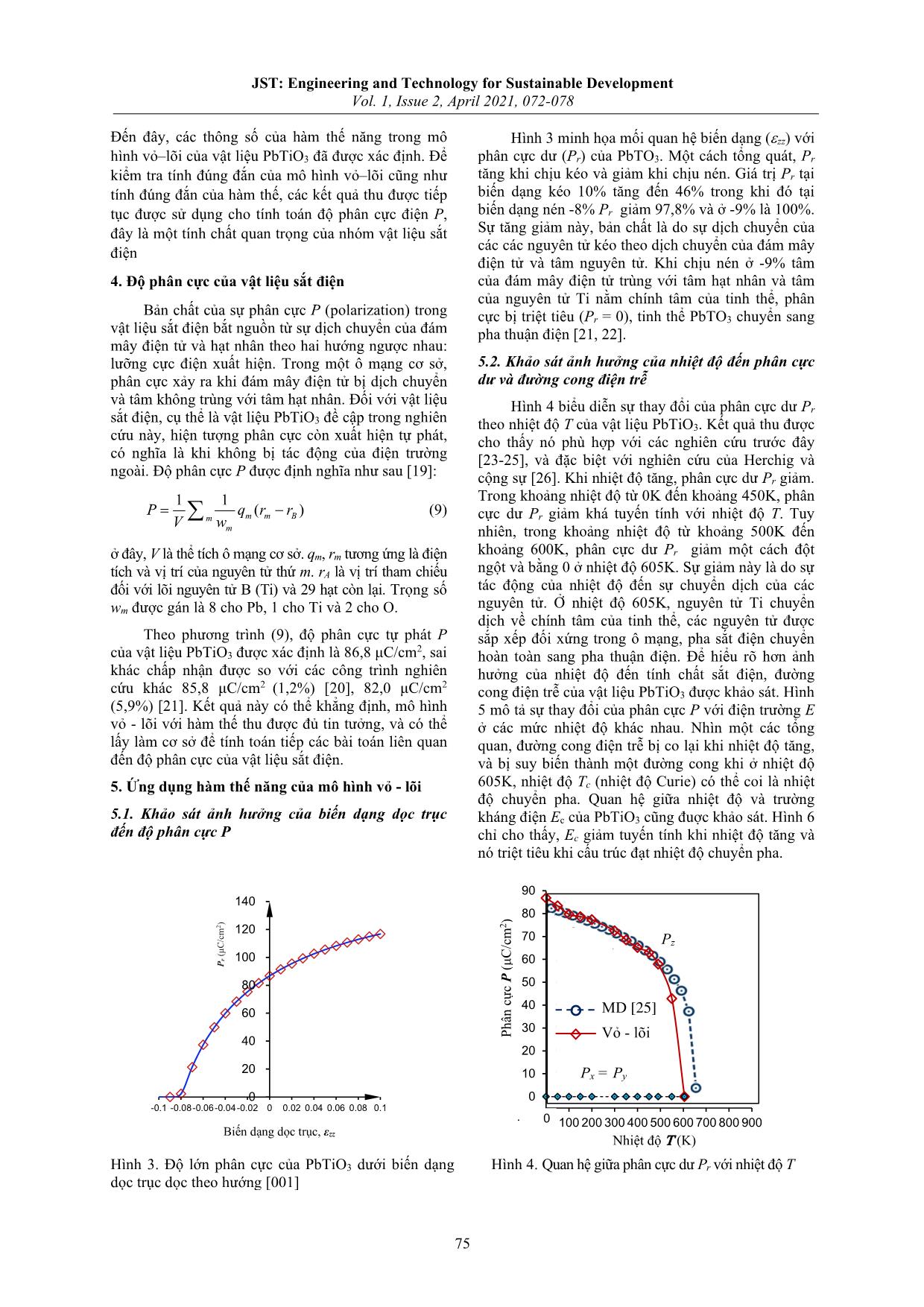
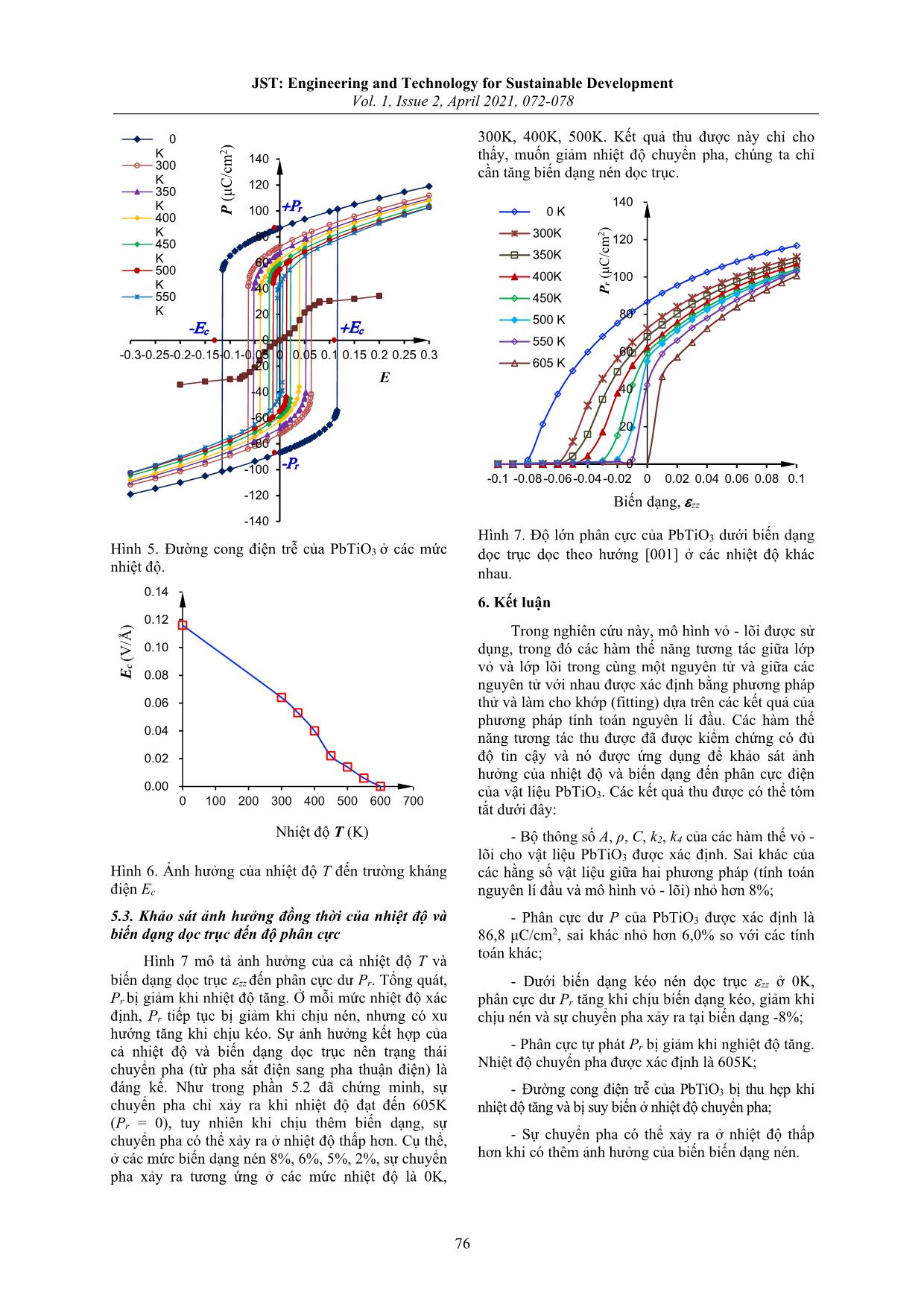
 JST: Engineering and Technology for Sustainable Development 
 Vol. 1, Issue 2, April 2021, 072-078 
 Xác định hàm thế năng của mô hình vỏ-lõi cho vật liệu sắt điện PbTiO3 và 
 ứng dụng trong tính toán độ phân cực 
 Evaluation of Potential Function of Core-Shell Model for PbTiO3 Ferroelectric Material and Its 
 Application for Polarization Calculation 
 Trần Thế Quang1,2*, Nguyễn Văn Hội1, Nguyễn Hoàng Linh1, 
 Vương Văn Thanh1, Đỗ Văn Trường1 
 1Viện Cơ khí, Trường Đại học Bách khoa Hà Nội, Hà Nội, Việt Nam 
 2Khoa Công nghệ, Trường Đại học Thái Bình, Thái Bình, Việt Nam 
 Email: tranthequang12@gmail.com 
 Tóm tắt 
 Trong nghiên cứu này, mô hình vỏ-lõi được sử dụng để xác định phân cực điện cho vật liệu sắt điện PbTiO3, 
 trong đó, các hàm thế năng tương tác giữa các nguyên tử được xác định bằng phương pháp thử và làm cho 
 khớp (fitting) dựa trên các kết quả từ tính toán nguyên lý đầu. Các chứng minh đã chỉ ra rằng phân cực dư 
 tăng khi chịu kéo và giảm khi chịu nén. Phân cực tự phát giảm khi nhiệt độ tăng. Sự chuyển pha từ pha sắt 
 điện sang pha thuận điện được phát hiện ở nhiệt độ 605K và sự chuyển pha này cũng có thể xảy ra ở nhiệt 
 độ thấp hơn (0K, 300K, 400K, 500K) khi có thêm biến dạng nén (8%, 6%, 5%, 2%, tương ứng). Đường cong 
 điện trễ bị co lại khi nhiệt độ tăng và bị suy biến thành một đường cong ở nhiệt độ 605K. 
 Từ khóa: PbTiO3, mô hình vỏ–lõi, phân cực sắt điện, ảnh hưởng của nhiệt độ, ảnh hưởng của biến dạng cơ 
 học. 
 Abstract 
 In this study, the core-shell model is used to calculate the electric polarization for PbTiO3 ferroelectric 
 material, in which, the interaction potential functions among atoms are determined by the fitting method 
 based on the results from the first principle calculation. The investigations obtained show that the remnant 
 polarization increases under tension and decreases under compression. The remnant polarization 
 decreases with increasing the temperature. The phase transition from the ferroelectric phase to the 
 paraelectric phase is determined at 605K and can occur at lower temperatures of 0K, 300K, 400K, 500K if 
 the compression strains are 8%, 6%, 5%, 2%, corresponding. The hysteresis loop shrinks as the 
 temperature increases and degrades into a curve at the temperature of 605K. 
 Keywords: PbTiO3, core-shell model, ferroelectric polarization, effect of temperature, effect of mechanical 
 strain. 
1. Giới thiệu* Như chúng ta đã biết, lý thuyết phiếm hàm mật 
 độ DFT (tính toán nguyên lí đầu) [5] dựa trên nền 
 Trong những năm gần đây, vật liệu sắt điện đã 
 tảng cơ học lượng tử là một phương pháp lý thuyết có 
và đang được sử dụng rộng rãi trong các linh kiện, 
 độ tin cậy cao và được sử dụng phổ biến trong các mô 
thiết bị điện tử như bộ nhớ truy cập ngẫu nhiên 
 phỏng xác định các tính chất của vật liệu sắt điện 
(FRAM) [1], cảm biến (sensor) [2], bộ chuyển đổi 
 [6-9]. Tuy nhiên, phương pháp này lại có hạn chế như 
điện (transducer) [3], tụ điện gốm [4], nhờ tính chất 
 chỉ có thể áp dụng cho các mô hình có số nguyên tử 
phân cực điện tự phát. Bản chất của sự phân cực điện 
 nhỏ (thường đến vài chục nguyên tử), thời gian tính 
là do sự chuyển dịch bất đối xứng của các nguyên tử 
 toán kéo dài và đặc biệt chỉ áp dụng cho tính toán mô 
trong ô đơn vị. Sự dịch chuyển này làm tâm của đám 
 phỏng ở nhiệt độ 0K. Trong những năm gần đây, mô 
mây điện tử không trùng với tâm của nguyên tử và nó 
 hình vỏ–lõi [10,11] xuất hiện, các tính toán mô phỏng 
tạo ra một lưỡng cực điện. Trong quá trình làm việc, 
 của mô hình này khắc phục được một số bất cập trong 
thiết bị có thể chịu tác dụng hoặc của biến dạng cơ 
 mô hình trước như: mô phỏng được bài toán có số 
học hoặc nhiệt, hoặc cả hai, làm các nguyên tử dịch 
 nguyên tử lớn (hàng trăm nghìn nguyên tử), tiệm cận 
chuyển và làm thay đổi phân cực điện thiết kế ban 
 tới kết cấu thực, thời gian tính toán nhanh, và đặc biệt 
đầu. Chính vì lí do đó, việc nghiên cứu ảnh hưởng 
 có thể tính toán mô phỏng khi thay đổi nhiệt độ. Tuy 
của biến dạng cơ học và nhiệt đến phân cực điện của 
 nhiên, trong mô hình vỏ–lõi, các hàm thế năng tương 
vật liệu sắt điện là một việc làm cần thiết nhằm nâng 
 tác giữa vỏ và lõi trong cùng nguyên tử và giữa các 
cao độ tin cậy phục vụ cũng như tuổi thọ của thiết bị. 
 nguyên tử với nhau cần được biết trước. Các hàm thế 
 năng này thường được xác định qua phương pháp 
ISSN: 2734-9381 thực nghiệm hoặc phương pháp mô phỏng. Chất 
https://doi.org/10.51316/jst.149.etsd.2021.1.2.12 
Received: February 02, 2020; accepted: May 01, 2020 
 72 
 JST: Engineering and Technology for Sustainable Development 
 Vol. 1, Issue 2, April 2021, 072-078 
lượng của bài toán mô phỏng phụ thuộc lớn vào độ 1124
 ECS( r ij ) = kr24ij + krij (4) 
chính xác của các hàm thế. 2 24
 Trong nghiên cứu này, mô hình vỏ–lõi được lựa 
 ở đây, qi, qj và rij lần lượt là điện tích của các nguyên 
chọn để tính toán, mô phỏng cho vật liệu P ...  trúc mạng tinh thể đơn vị của mô hình vật liệu trong tính toán mô hình vỏ - lõi và 
PbTiO3 nguyên lí đầu được thiết lập như nhau. 
 Cấu trúc cân bằng được thực hiện ở cả mô hình 3.3. Kết quả của bài toán tối ưu 
chưa chịu biến dạng và chịu biến dạng qua sử dụng Bảng 1 trình bày kết quả các hàm kì vọng thu 
giải thuật cực tiểu Broyden-Fretcher-Goldfarb- được qua bài toán tối ưu. Hằng số mạng tinh thể và 
Shanno (BFGS) dưới lực Hellmann Feynman và các hằng số đàn hồi thu được sai khác nhỏ hơn 8% so với 
thành phần ứng suất nhỏ hơn 5.0×10-4 Ry/a.u và 
 -3 kết quả tính toán nguyên lí đầu. Kết quả này là cơ sở 
10 GPa, tương ứng. để thu được bộ thông số của các hàm thế, tổng hợp 
 Sau khi cấu trúc được cân bằng (cấu trúc ở trạng trong bảng 2. 
thái năng lượng thấp nhất), hằng số mạng a và c được 
 Bảng 1. Các tính chất cơ học của PbTiO3 thu được từ 
xác định, trong khi đó, các hằng số đàn hồi Cij được tối ưu hóa mô hình vỏ–lõi và tính toán nguyên lí đầu. 
tính toán từ đạo hàm bậc 2 của tổng năng lượng E qua 
công thức sau: Phương pháp nguyên 
 1 ∂2 E Mô hình lí đầu Sai khác 
 C= (ij ,= 1 ÷ 6) (5) Thông số 
 ij V ∂∂εε vỏ - lõi Nghiên cứu lớn nhất 
 ij [17] 
 hiện tại 
với V là thể tích ô mạng cơ sở và biến dạng εi, εj được 
 a (Å) 3,878 3,863 3,867 0,39% 
định nghĩa như sau: 
 c (Å) 4,069 4,037 4,042 0,80% 
 ε1 = ε11 ε2 = ε22 ε3 = ε33 (6) 
 c/a 1,049 1,045 1,045 0,38% 
 ε4 = ε23 + ε32 ε5 = ε13 + ε31 ε6 = ε12 + ε21 (7) 
 V (Å3) 61,193 60,243 60,443 1,57% 
3.2. Thủ tục tối ưu xác định hàm thế năng 
 C11 (GPa) 286,922 287,90 284,30 0,92% 
 Trong phương pháp tối ưu tìm các hằng số vật C12 (GPa) 118,743 117,10 114,60 3,61% 
liệu, hàm mục tiêu được đưa ra dưới dạng sau: 
 2 C13 (GPa) 92,079 92,60 91,60 -0,57% 
 fpm ()− fmt
 = ii (8) 
 Fp( ) ∑ i wi mt C33 (GPa) 101,237 100,60 98,60 2,67% 
 fi
 C44 (GPa) 61,278 62,80 61,00 -2,48% 
 mt m
ở đây, fi , fpi () và wi lần lượt là giá trị đích C66 (GPa) 110,716 107,90 103,10 7,39% 
(target value) thu được từ tính toán nguyên lí đầu, giá 
trị kỳ vọng và trọng số. Giá trị trọng số ban đầu và sai 
số chính xác được chọn là 1000 và ±1% [17], tương 
ứng. 
Bảng 2. Các thông số của các hàm thế năng trong mô hình vỏ–lõi cho PbTiO3 
 -2 -4
 Nguyên tử qc (e) qe (e) k2 (eV Å ) k4 (eV Å ) 
 Pb +5,317864 -3,606888 129,408999 41861,509708 
 Ti +19,397344 -16,267976 8428,836044 99652150,211023 
 Tương tác A (eV) ρ (Å) C (eV Å6) 
 Pb–O 2501,105048 0,306122 0,231585 
 O–O 1139,341138 0,266229 72,673182 
 Ti–O 2559,834378 0,282161 5,350582 
 Pb–Ti 464,653659 0,398264 206,772977 
 74 
 JST: Engineering and Technology for Sustainable Development 
 Vol. 1, Issue 2, April 2021, 072-078 
Đến đây, các thông số của hàm thế năng trong mô Hình 3 minh họa mối quan hệ biến dạng (εzz) với 
hình vỏ–lõi của vật liệu PbTiO3 đã được xác định. Để phân cực dư (Pr) của PbTO3. Một cách tổng quát, Pr 
kiểm tra tính đúng đắn của mô hình vỏ–lõi cũng như tăng khi chịu kéo và giảm khi chịu nén. Giá trị Pr tại 
tính đúng đắn của hàm thế, các kết quả thu được tiếp biến dạng kéo 10% tăng đến 46% trong khi đó tại 
tục được sử dụng cho tính toán độ phân cực điện P, biến dạng nén -8% Pr giảm 97,8% và ở -9% là 100%. 
đây là một tính chất quan trọng của nhóm vật liệu sắt Sự tăng giảm này, bản chất là do sự dịch chuyển của 
 các các nguyên tử kéo theo dịch chuyển của đám mây 
điện 
 điện tử và tâm nguyên tử. Khi chịu nén ở -9% tâm 
4. Độ phân cực của vật liệu sắt điện của đám mây điện tử trùng với tâm hạt nhân và tâm 
 của nguyên tử Ti nằm chính tâm của tinh thể, phân 
 Bản chất của sự phân cực P (polarization) trong 
 cực bị triệt tiêu (Pr = 0), tinh thể PbTO3 chuyển sang 
vật liệu sắt điện bắt nguồn từ sự dịch chuyển của đám pha thuận điện [21, 22]. 
mây điện tử và hạt nhân theo hai hướng ngược nhau: 
lưỡng cực điện xuất hiện. Trong một ô mạng cơ sở, 5.2. Khảo sát ảnh hưởng của nhiệt độ đến phân cực 
phân cực xảy ra khi đám mây điện tử bị dịch chuyển dư và đường cong điện trễ 
và tâm không trùng với tâm hạt nhân. Đối với vật liệu 
 Hình 4 biểu diễn sự thay đổi của phân cực dư Pr 
sắt điện, cụ thể là vật liệu PbTiO3 đề cập trong nghiên 
 theo nhiệt độ T của vật liệu PbTiO3. Kết quả thu được 
cứu này, hiện tượng phân cực còn xuất hiện tự phát, cho thấy nó phù hợp với các nghiên cứu trước đây 
có nghĩa là khi không bị tác động của điện trường [23-25], và đặc biệt với nghiên cứu của Herchig và 
ngoài. Độ phân cực P được định nghĩa như sau [19]: 
 cộng sự [26]. Khi nhiệt độ tăng, phân cực dư Pr giảm. 
 11 Trong khoảng nhiệt độ từ 0K đến khoảng 450K, phân 
 = − 
 P∑ qrmm() r B (9) cực dư Pr giảm khá tuyến tính với nhiệt độ T. Tuy 
 Vwm
 m nhiên, trong khoảng nhiệt độ từ khoảng 500K đến 
ở đây, V là thể tích ô mạng cơ sở. qm, rm tương ứng là điện khoảng 600K, phân cực dư Pr giảm một cách đột 
tích và vị trí của nguyên tử thứ m. rA là vị trí tham chiếu ngột và bằng 0 ở nhiệt độ 605K. Sự giảm này là do sự 
đối với lõi nguyên tử B (Ti) và 29 hạt còn lại. Trọng số tác động của nhiệt độ đến sự chuyển dịch của các 
wm được gán là 8 cho Pb, 1 cho Ti và 2 cho O. nguyên tử. Ở nhiệt độ 605K, nguyên tử Ti chuyển 
 dịch về chính tâm của tinh thể, các nguyên tử được 
 Theo phương trình (9), độ phân cực tự phát P sắp xếp đối xứng trong ô mạng, pha sắt điện chuyển 
 2
của vật liệu PbTiO3 được xác định là 86,8 μC/cm , sai hoàn toàn sang pha thuận điện. Để hiểu rõ hơn ảnh 
khác chấp nhận được so với các công trình nghiên hưởng của nhiệt độ đến tính chất sắt điện, đường 
 2 2
cứu khác 85,8 μC/cm (1,2%) [20], 82,0 μC/cm cong điện trễ của vật liệu PbTiO3 được khảo sát. Hình 
(5,9%) [21]. Kết quả này có thể khẳng định, mô hình 5 mô tả sự thay đổi của phân cực P với điện trường E 
vỏ - lõi với hàm thế thu được đủ tin tưởng, và có thể ở các mức nhiệt độ khác nhau. Nhìn một các tổng 
lấy làm cơ sở để tính toán tiếp các bài toán liên quan quan, đường cong điện trễ bị co lại khi nhiệt độ tăng, 
đến độ phân cực của vật liệu sắt điện. và bị suy biến thành một đường cong khi ở nhiệt độ 
5. Ứng dụng hàm thế năng của mô hình vỏ - lõi 605K, nhiệt độ Tc (nhiệt độ Curie) có thể coi là nhiệt 
 độ chuyển pha. Quan hệ giữa nhiệt độ và trường 
5.1. Khảo sát ảnh hưởng của biến dạng dọc trục kháng điện Ec của PbTiO3 cũng đuợc khảo sát. Hình 6 
đến độ phân cực P chỉ cho thấy, Ec giảm tuyến tính khi nhiệt độ tăng và 
 nó triệt tiêu khi cấu trúc đạt nhiệt độ chuyển pha. 
 90
 140
 80
 )
 )
 2
 2 120
 70 Pz 
 (μC/cm
 C/cm
 r 100
 μ
 P 60
 (
 P 50
 80 c 
 ự 
 40 
 60 MD [25] 
 30
 Phân c Phân Vỏ - lõi 
 40
 20
 20
 10 Px = Py 
 0 0
 -0.1 -0.08-0.06-0.04-0.02 0 0.02 0.04 0.06 0.08 0.1
 -10 0 100 200 300 400 500 600 700 800 900
 Biến dạng dọc trục, εzz 
 Nhiệt độ T (K) 
Hình 3. Độ lớn phân cực của PbTiO3 dưới biến dạng Hình 4. Quan hệ giữa phân cực dư Pr với nhiệt độ T 
dọc trục dọc theo hướng [001] 
 75 
 JST: Engineering and Technology for Sustainable Development 
 Vol. 1, Issue 2, April 2021, 072-078 
 0 300K, 400K, 500K. Kết quả thu được này chỉ cho 
 )
 K 2 140 thấy, muốn giảm nhiệt độ chuyển pha, chúng ta chỉ 
 300
 K cần tăng biến dạng nén dọc trục. 
 C/cm 120
 350 μ
 (
 K +Pr 140
 P 100 0 K
 400
 )
 K 80 300K 2
 450 120
 350K
 K 60
 500 (μC/cm
 400K 100
 K r
 40 P
 550 450K
 K
 20 500 K 80
 -Ec +Ec 
 0 550 K
 -0.3-0.25-0.2-0.15-0.1-0.05 0 0.05 0.1 0.15 0.2 0.25 0.3 60
 -20 605 K
 E 
 40
 -40 
 -60
 20
 -80
 -100 -Pr 0
 -0.1 -0.08-0.06-0.04-0.02 0 0.02 0.04 0.06 0.08 0.1
 -120
 Biến dạng, εzz 
 -140 
 Hình 7. Độ lớn phân cực của PbTiO3 dưới biến dạng 
Hình 5. Đường cong điện trễ của PbTiO3 ở các mức dọc trục dọc theo hướng [001] ở các nhiệt độ khác 
nhiệt độ. nhau. 
 0.14
 6. Kết luận 
 0.12
 Trong nghiên cứu này, mô hình vỏ - lõi được sử 
 0.10 dụng, trong đó các hàm thế năng tương tác giữa lớp 
 (V/Å)
 c vỏ và lớp lõi trong cùng một nguyên tử và giữa các 
 E 0.08
 nguyên tử với nhau được xác định bằng phương pháp 
 0.06 thử và làm cho khớp (fitting) dựa trên các kết quả của 
 phương pháp tính toán nguyên lí đầu. Các hàm thế 
 0.04 năng tương tác thu được đã được kiểm chứng có đủ 
 0.02 độ tin cậy và nó được ứng dụng để khảo sát ảnh 
 hưởng của nhiệt độ và biến dạng đến phân cực điện 
 0.00
 của vật liệu PbTiO3. Các kết quả thu được có thể tóm 
 0 100 200 300 400 500 600 700
 tắt dưới đây: 
 Nhiệt độ T (K) - Bộ thông số A, ρ, C, k2, k4 của các hàm thế vỏ - 
 lõi cho vật liệu PbTiO3 được xác định. Sai khác của 
Hình 6. Ảnh hưởng của nhiệt độ T đến trường kháng các hằng số vật liệu giữa hai phương pháp (tính toán 
điện Ec nguyên lí đầu và mô hình vỏ - lõi) nhỏ hơn 8%; 
5.3. Khảo sát ảnh hưởng đồng thời của nhiệt độ và - Phân cực dư P của PbTiO3 được xác định là 
biến dạng dọc trục đến độ phân cực 86,8 μC/cm2, sai khác nhỏ hơn 6,0% so với các tính 
 toán khác; 
 Hình 7 mô tả ảnh hưởng của cả nhiệt độ T và 
biến dạng dọc trục εzz đến phân cực dư Pr. Tổng quát, - Dưới biến dạng kéo nén dọc trục εzz ở 0K, 
Pr bị giảm khi nhiệt độ tăng. Ở mỗi mức nhiệt độ xác phân cực dư Pr tăng khi chịu biến dạng kéo, giảm khi 
định, Pr tiếp tục bị giảm khi chịu nén, nhưng có xu chịu nén và sự chuyển pha xảy ra tại biến dạng -8%; 
hướng tăng khi chịu kéo. Sự ảnh hưởng kết hợp của 
cả nhiệt độ và biến dạng dọc trục nên trạng thái - Phân cực tự phát Pr bị giảm khi nghiệt độ tăng. 
chuyển pha (từ pha sắt điện sang pha thuận điện) là Nhiệt độ chuyển pha được xác định là 605K; 
đáng kể. Như trong phần 5.2 đã chứng minh, sự - Đường cong điện trễ của PbTiO3 bị thu hẹp khi 
chuyển pha chỉ xảy ra khi nhiệt độ đạt đến 605K nhi ệt độ tăng và bị suy biến ở nhiệt độ chuyển pha; 
(Pr = 0), tuy nhiên khi chịu thêm biến dạng, sự 
chuyển pha có thể xảy ra ở nhiệt độ thấp hơn. Cụ thể, - Sự chuyển pha có thể xảy ra ở nhiệt độ thấp 
ở các mức biến dạng nén 8%, 6%, 5%, 2%, sự chuyển hơn khi có thêm ảnh hưởng của biến biến dạng nén. 
pha xảy ra tương ứng ở các mức nhiệt độ là 0K, 
 76 
 JST: Engineering and Technology for Sustainable Development 
 Vol. 1, Issue 2, April 2021, 072-078 
Lời cảm ơn simulations of materials, J.Phys. Condens. Matter 
 21(9) (2009) 395502, 
 Nghiên cứu này được tài trợ bởi Quỹ Phát triển 
  10.1088/0953-8984/21/39/395502. 
Khoa học và Công nghệ Quốc gia (NAFOSTED), mã 
số: 107.02- 2016.18. [13] D. M. Ceperley and B. J. Alder, Ground State of the 
 Electron Gas by a Stochastic Method, Phys. Rev. 
Tài liệu tham khảo Lett. 45(7) (1980) 566–569, 
[1] J.F. Scott, C. A. Paz de Araujo, Ferroelectric  10.1103/PhysRevLett.45.566. 
 memories, Science 246(4936) (1989) 1400-1405, 
 [14] J.P. Perdew & A. Zunger, Self-interaction correction 
  to density-functional approximations for many-
[2] L.E. Cross, Ferroelectric Materials for electron systems, Phys. Rev. B 23(10) (1981) 5048–
 Electromechanical Transducer Applications. Jpn. J. 5079, 
 Appl. Phys, 34 (Part 1, No. 5B) (1995) 2525–2532,  10.1103/PhysRevB.23.5048. 
  10.1143/JJAP.34.2525. [15] D. Vanderbilt, Soft self-consistent pseudopotentials 
 in a generalized eigenvalue formalism, Phys. Rev. B 
[3] S. Zhang, F. Li, X. Jiang, J. Kim, J. Luo & X. Geng, 41 (1990) 7892-7895, 
 Advantages and challenges of relaxor-PbTiO3 
 ferroelectric crystals for electroacoustic transducers–  10.1103/PhysRevB.41.7892. 
 A review, Prog. Mater. Sci. 68 (2015) 1–66, [16] H.J. Monkhorst and J.D. Pack, Special points for 
  10.1016/j.pmatsci.2014.10.002. Brillouin-zone integrations, Phys. Rev. B 13 (1976) 
 5188-5192, 
[4] P.P. Khirade, S.D. Birajdar, A.V. Raut & K.M. 
  10.1103/PhysRevB.13.5188. 
 Jadhav, Multiferroic iron doped BaTiO3 
 nanoceramics synthesized by sol-gel auto [17] T. Kitamura, Y. Umeno, F. Shang, T. Shimada, and 
 combustion: Influence of iron on physical properties, K. Wakahara, “Development of Interatomic Potential 
 Ceram. Int. (2016) 1-11, for Pb(Zr,Ti)O3 Based on Shell model,” J. Solid 
  10.1016/j.ceramint.2016.05.021. Mech. Mater. Eng., vol. 1, no. 12 (2007) 1423–1431, 
[5] M.A. Morales, R. Clay, C. Pierleoni, D.M. Ceperley, 
 First-principle methods: A perspective from quantum [18] J.D. Gale, A.L. Rohl, The General Utility Lattice 
 Monte Carlo, Entropy. 16(1) (2013) 287–321, Program (GULP), Mol. Simul, Vol. 29, No. 5 (2003) 
  10.3390/e16010287. 291-341, 
[6] S. Tinte et al, Atomistic modelling of BaTiO3 based 
 on first-principles calculations, J.Phys. Condens. [19] M. Sepliarsky and R.E. Cohen, First-principles based 
 Matter. 11 (1999) 9679-9690, atomistic modeling of phase stability in PMN–xPT, J. 
  10.1088/0953-8984/11/48/325. Phys. Condens. Matter. 23(43) (2011) 435902, 
[7] R.E. Cohen, Origin of ferroelectricity in perovskite 
 oxides, Nature 358(6382) (1992) 136–138, [20] T. Kitamura, Y. Umeno, F. Shang, T. Shimada, and 
  10.1038/358136a0. K. Wakahara, Development of Interatomic Potential 
 for Pb(Zr,Ti)O3 Based on Shell model, J. Solid Mech. 
[8] B. Meyer, J. Padilla, & D. Vanderbilt, Theory of Mater. Eng., vol. 1, no. 12 (2007) 1423–1431, 
 PbTiO3, BaTiO3, and SrTiO3 surfaces, Faraday 
 Discussions 114 (1999) 395–405,  
  https://doi.org/10.1039/A903029H. [21] H.N. Lee, S.M. Nakhmanson, M.F. Chisholm, H.M. 
 Christen, K.M. Rabe & D. Vanderbilt, Suppressed 
[9] C. Bungaro & K.M. Rabe, Coexistence of Dependence of Polarization on Epitaxial Strain in 
 antiferrodistortive and ferroelectric distortions at the Highly Polar Ferroelectrics, Phys. Rev. Lett. 98 
 PbTiO3 (001) surface, Phys. Rev. B 71(3) (2005) (2007) 217602, 
 035420(9), 
  10.1103/PhysRevB.71.035420.  
 [22] M. Sepliarsky and R.E. Cohen, Development of a 
[10] H.J. Mang & H.A. Weidenmuller, Shell-Model 
 Theory of the Nucleus, Annu. Rev. Nucl. Sci.18(1) Shell Model Potential for Molecular Dynamics for 
 (1968) 1–26, PbTiO3 by Fitting First Principles Results, Am. Inst. 
 Phvsics, Vol. 36 (2002) 36-44, 
  10.1063/1.1499550. 
[11] B.G. Dick & A.W. Overhauser, Theory of the 
 Dielectric Constants of Alkali Halide Crystals, Phys. [23] R.K. Behera, Effect of surfaces, domain walls and 
 Rev. 112(1) (1958) 90–103, grain boundaries on ferroelectricity in lead titanate 
 using atomic scale simulations, University of florida, 
  10.1103/PhysRev.112.90. 2009, 
[12] P. Giannozzi et al, Quantum espresso: a modular and [24] O. Gindele, A. Kimmel, M.G. Cain & D. Duffy, 
 open-source software project for quantum Shell Model force field for Lead Zirconate Titanate 
 77 
 JST: Engineering and Technology for Sustainable Development 
 Vol. 1, Issue 2, April 2021, 072-078 
 Pb(Zr1–xTix)O3, J. Phys. Chem. C 119(31) (2015) [26] R. Herchig, C.-M. Chang, B. K. Mani & I. 
 17784–17789, Ponomareva, Electrocaloric effect in ferroelectric 
  10.1021/acs.jpcc.5b03207. nanowires from atomistic simulations, Sci. Rep 5 
 (2015) 1-6, 
[25] V.G. Bhide, K.G. Deshmukh & M.S. Hegde,  10.1038/srep17294. 
 Ferroelectric properties of PbTiO3, Physica 28(9) 
 (1962) 871–876, 
  10.1016/0031-8914(62)90075-7. 
 78