Ứng dụng mô hình thống kê và mạng nơ-ron lan truyền ngược trong phân tích dự báo chuyển dịch đập thủy điện

 VNU Journal of Science: Earth and Environmental Sciences, Vol. 37, No. 1 (2021) 44-51 
 Original Article 
 Application of Statistic Model and Backpropagation Neural 
 Network to Analyzing and Forecasting Hydropower Dam 
 Displacement 
 Bui Thi Kien Trinh1,*, Xiao Yangxuan2, Chinh Van Doan3, 
 Do Xuan Khanh1, Tran The Viet1, Mai Dinh Sinh3 
 1Thuyloi University, 175 Tay Son, Hanoi, Vietnam 
 2School of Geodesy and Geomatics, Wuhan University, 
 129 Louyu Road, Wuhan, Hubei Province, P.R. China, 430079 
 3Military Technical Academy, 236 Hoang Quoc Viet, Hanoi, Vietnam 
 Received 23 December 2019 
 Revised 16 January 2020; Accepted 18 January 2020 
 Abstract: Horizontal displacement of Hoa Binh dam in operation phase was analyzed and then 
 forecasted by using three methods: the multi-regression model (MTR), the Seasonal Integrated 
 Auto-regressive Moving Average (SARIMA) and the Back-propagation Neural Network (BPNN). 
 The monitoring data of the Hoa Binh Dam in 137 periods, including horizontal displacement, time, 
 reservoir water level and air temperature were used for the experiments. The results indicated that 
 all of these three methods could describe the real trend of dam deformation and achieve the required 
 accuracy in short-term forecast up to 9 months. In addition, forecast results of BPNN had the highest 
 stability and accuracy. 
 Keywords: Horizontal displacement, Multi-regression model, Seasonal ARIMA, Back-propagation 
 neural network.*
________ 
* Corresponding author. 
 E-mail address: bktrinh@tlu.edu.vn 
 https://doi.org/10.25073/2588-1094/vnuees.4529 
 44 
 B.T.K. Trinh et al. / VNU Journal of Science: Earth and Environmental Sciences, Vol. 37, No. 1 (2021) 44-51 45 
 Ứng dụng mô hình thống kê và mạng nơ-ron lan truyền ngược 
 trong phân tích dự báo chuyển dịch đập thủy điện 
 Bùi Thị Kiên Trinh1,*, Xiao Yangxuan2, Đoàn Văn Chinh3, 
 Đỗ Xuân Khánh1, Trần Thế Việt1, Mai Đình Sinh3 
 1Trường Đại học Thủy lợi, 175 Tây Sơn, Hà Nội, Việt Nam 
 2School of Geodesy and Geomatics, Wuhan University, 
 129 Louyu Road, Wuhan, Hubei Province, P.R. China, 430079 
 3Học viện Kỹ thuật Quân sự, 236 Hoàng Quốc Việt, Hà Nội, Việt Nam 
 Nhận ngày 23 tháng 12 năm 2019 
 Chỉnh sửa ngày 16 tháng 01 năm 2020; Chấp nhận đăng ngày 18 tháng 01 năm 2020 
 Tóm tắt: Mô hình thống kê hồi quy bội, chuỗi thời gian theo mùa và mạng nơ-ron lan truyền ngược 
 được ứng dụng để phân tích và dự báo chuyển dịch ngang của đập thủy điện Hoà Bình ở giai đoạn 
 vận hành. Dữ liệu thực nghiệm là kết quả quan trắc chuyển dịch ngang, mực nước hồ và nhiệt độ 
 không khí trong 137 chu kỳ quan trắc. Kết quả cho thấy các mô hình này hoàn toàn phù hợp với 
 chuyển dịch thực tế của đập và đạt yêu cầu về độ chính xác dự báo theo chỉ tiêu sai số trung phương 
 và sai số trung bình với khoảng thời gian dự báo dưới 9 tháng. Thêm vào đó, mạng nơ-ron lan truyền 
 ngược có độ chính xác cao và ổn định hơn 2 loại mô hình thống kê hồi quy bội và chuỗi thời gian 
 theo mùa trong phân tích, dự báo chuyển dịch đập. 
 Từ khoá: Chuyển dịch ngang, mô hình hồi quy bội, chuỗi thời gian theo mùa, mạng nơ-ron lan 
 truyền ngược. 
1. Mở đầu* dịch sẽ được so sánh với chu kỳ đầu tiên để xác 
 định các yếu tố [5]: 
 Thủy điện đóng vai trò chủ lực của hệ thống - Độ lớn và hướng của chuyển dịch; 
điện toàn quốc, góp phần không nhỏ trong các - Độ chuyển dịch trung bình trên toàn công 
thành tựu phát triển kinh tế xã hội của Việt Nam. trình, độ chênh lệch chuyển dịch theo 1 trục nhất 
Do vậy việc quan trắc giám sát an toàn của đập định (đặc trưng cho độ xoay của công trình); 
thủy điện là vô cùng thiết yếu [1-4].1 - Tốc độ chuyển dịch và tốc độ trung bình 
 Những chuyển dịch trên bề mặt của đập theo của từng điểm theo thời gian; 
phương thẳng đứng và nằm ngang thường được - Chuyển dịch trong không gian của toàn 
quan trắc bằng phương pháp trắc địa tuân thủ các công trình và trọng tâm công trình theo đường 
bộ tiêu chuẩn quốc gia TCVN 9399-2012 [5], thẳng hoặc mặt phẳng xác suất. 
TCVN 8215-2009 [6], TCVN 9360-2012 [7], Dựa vào các yếu tố nêu trên, một số nghiên 
TCVN 9400-2012 [8]. Sau đó, các giá trị chuyển cứu trong nước vể xây dựng mô hình phân tích 
 dự báo chuyển dịch đập được công bố tập trung 
________ 
* Tác giả liên hệ. 
 Địa chỉ email: bktrinh@tlu.edu.vn 
 https://doi.org/10.25073/2588-1094/vnuees.4529 
46 B.T.K. Trinh et al. / VNU Journal of Science: Earth and Environmental Sciences, Vol. 37, No. 1 (2021) 44-51 
 3
vào mối tương quan tuyến tính của chuỗi kết quả 훿푡 = 1 + 2√푡 + 2 √푡 + 4ln⁡(푡) là tác 
quan trắc với mực nước hồ chứa có tính ảnh nhân thời gian, t là tuổi đập tính theo ngày. 
hưởng của độ trễ sử dụng hàm số sin và cos Các hệ số 푖, 푗, 1−4 được xác định từ cặp 
[9,10]. giá trị chuyển dịch đập và tác nhân tương ứng 
 Tuy nhiên, các nghiên cứu trên thế giới đã trong mỗi chu kỳ quan trắc theo nguyên lý số 
chỉ ra rằng chuyển dịch đập là quá trình phi tuyến bình phương nhỏ nhấ ... a chuỗi 
 - Sự giãn nở nhiệt của đập; Chuỗi 푌푡 được coi là ổn định (hay chuỗi 
 - Tuổi của đập tính theo thời gian vận hành dừng) khi có tất cả những đặc điểm sau: 
thực tế. (푌푡) = 휇 (2) 
 2 2
 Mô hình hồi quy bội MTR (Multi- (푌푡) = (푌푡 − 휇) = 휎 (3) 
regression) tổng quát thể hiện mối quan hệ giữa 표푣(푌푡, 푌푡+ ) = 훾 = [(푌푡 − 휇)(푌푡+ − 휇)] (4) 
chuyển dịch đập với những tác nhân nêu trên Trong đó E, Var, Cov lần lượt là kỳ vọng, 
được thể hiện dưới dạng như sau: phương sai và hiệp phương sai. 
 훿 = 훿 + 훿 + 훿푡 (1) Kiểm định ADF (Augmented Dickey-Fuller) 
 trong đó: được sử dụng phổ biến nhất để kiểm tra tính ổn 
 푛 푖
 훿 = ∑푖=0 푖 là tác nhân áp lực do hồ định của các chuỗi thời gian. 
chứa, H là mực nước thượng lưu; 2.2.2. Xử lý chuỗi không ổn định 
 훿 = ∑ là tác nhân giãn nở nhiệt của 
 푗=1 푗 푗 Trong thực tế hầu hết các số liệu thu được 
đập, T là nhiệt độ của môi trường; đều là chuỗi không ổn định, do vậy cần biến đổi 
 chuỗi bằng cách lấy sai phân 푊푡: 
 B.T.K. Trinh et al. / VNU Journal of Science: Earth and Environmental Sciences, Vol. 37, No. 1 (2021) 44-51 47 
 푊푡 = 푌푡 − 푌푡−1 (5) 2.3. Mô hình mạng nơ-ron lan truyền ngược BPNN 
 Nếu sai phân bậc d của chuỗi 푌푡 thỏa mãn cả 
3 điều kiện ổn định (2), (3) và (4) thì chuỗi được 
gọi là ổn định bậc d. 
 2.2.3. Chọn bậc AR(p) và MA(q) tối ưu 
 Mô hình AR(p): 
푌푡 = 0 + 1푌푡−1 + 2푌푡−2 + ⋯ + 푌푡− + 푒푡 (6) 
 Mô hình MA(q): 
푌푡 = 0 + 푒푡 + 1푒푡−1 + 2푒푡−2 + ⋯ + 푞푒푡−푞 (7) 
 trong đó: 
 0, 1,  , là tham số phân tích hồi quy, 
thỏa mãn: 0 + 1 + ⋯ + < 1 (8) Hình 1. Cấu trúc của BPNN. 
 , ,  , là giá trị trung bình của 푌 và các 
 0 1 푞 푡 Mạng nơ-ron lan truyền ngược BPNN 
hệ số bình quân di động, thỏa mãn: 
 (Backpropagation Neural Network) là một trong 
 + + ⋯ + < 1 (9) 
 1 2 푞 những mạng thần kinh nhân tạo phổ biến nhất. 
 푒푡, 푒푡−1, 푒푡−2,  , 푒푡−푞 là sai số ngẫu nhiên Về nguyên lý, đây là hệ thống tính toán mô 
tương ứng của 푌푡, 푌푡−1, 푌푡−2,  , 푌푡−푞. phỏng hoạt động của các nơ-ron trong hệ thần 
 Sử dụng hàm tự tương quan ACF (Auto- kinh, bao gồm 3 lớp cơ bản: 
correlation Function) để chọn bậc q cho mô hình 
 Số lớp ẩn và số nơ-ron trong mỗi lớp thường 
MA và hàm tự tương quan từng phần PACF 
 được chọn dựa vào những mô hình có sẵn hoặc 
(Partial Auto-correlation Function) để chọn bậc 
 theo kinh nghiệm. 
p cho mô hình AR (là những giá trị nằm ngoài 
khoảng tin cậy, giảm đột ngột). Ngoài ra yếu tố Giải thuật lan truyền ngược trong mô hình 
mùa vụ s cũng thể hiện rất rõ trên biểu đồ ACF mạng nơ-ron là công cụ tính toán mạnh mẽ, có 
và PACF. thể dễ dàng thực thi với 2 quá trình (i) lan truyền 
 tiến và (ii) lan truyền ngược bao gồm các bước 
 2.2.4. Ước lượng mô hình ARIMA(p,d,q) và sau [13]: 
chọn mô hình tối ưu 
 2.3.1. Tính toán lan truyền tiến 
 Mô hình ARIMA(p,d,q) là mô hình hỗn hợp 
của AR(p) và MA(q) đã sai phân hoá ở bậc d thỏa Giá trị của các nơ-ron trong lớp ẩn và lớp đầu 
mãn cả 2 điều kiện (8), (9). ra được tính theo các công thức sau: 
 푛
 Kết hợp yếu tố mùa vụ s và tổ hợp các giá trị 푠 푗 = ∑푖=1 푊푖푗 푖 (10) 
{0, 1,..., p}, {1, 2,..., d}, {0, 1,..., q} xác định 
 푗 = (푠 푗) (11) 
được ở bước trên để thành lập mô hình 
 trong đó: 
SARIMA( , , 푞)푠. Mô hình tối ưu được lựa chọn 
dựa trên 2 tiêu chí: 푊푖푗 là trọng số liên kết nơ-ron i trong lớp 
 - Là nhiễu trắng. trước với nơ-ron j trong lớp hiện thời; 
 - Có giá trị AIC (Akaike Information 푖 là giá trị đầu ra của nơ-ron i trong lớp 
Criterion) nhỏ nhất. trước; 
 Tính các tham số cho mô hình tối ưu đã chọn 
 푗 là giá trị đầu ra của nơ-ron j trong lớp hiện 
bằng quá trình lặp, kiểm định độ chính xác và thời; 
phù hợp của mô hình với chuỗi dữ liệu ban đầu. 
 là hàm kích hoạt, thường sử dụng hàm 
 2.2.5. Dự báo Sigmoid với hằng số c chọn tuỳ ý [2,13]: 
 Sử dụng mô hình đã thiết lập ở bước trên để 1
 ( ) = (12) 
tiến hành dự báo ngắn hạn các giá trị 1+푒− 
푌푡+1, 푌푡+2, ⁡ trong giai đoạn tiếp theo. 
48 B.T.K. Trinh et al. / VNU Journal of Science: Earth and Environmental Sciences, Vol. 37, No. 1 (2021) 44-51 
 Theo đó, giá trị của các nơ-ron trong lớp ẩn trong lớp ẩn sẽ được cập nhật theo các công thức 
và lớp đầu ra được xác định từ giá trị của nơ-ron (14-16). 
trong lớp đầu vào. 2.3.4. Cập nhật trọng số 
 2.3.2. Lan truyền ngược ở lớp đầu ra Điều quan trọng cần lưu ý là đến bước này, 
 Tính sai số của giá trị nơ-ron ở lớp đầu ra các trọng số của vòng huấn luyện sau mới được 
theo công thức: cập nhật. Nói cách khác, không được cập nhật 
 ngay bất kỳ trọng số nào dù đã được tính ra cho 
 휀푗 = 푗(1 − 푗) ( 푗 − 푗) (13) đến khi sai số của tất cả các nơ-ron trong mạng 
 trong đó: được tính toán xong, bởi kết quả sẽ không hợp lệ 
 휀푗 là sai số của nơ-ron j trong lớp đầu ra; nếu trọng số mới của kỳ huấn luyện sau được sử 
 dụng để tính sai số trong kỳ huấn luyện hiện thời. 
 là giá trị mong muốn của nơ-ron j trong 
 푗 Giá trị sai số mới có thể được xác định từ các 
lớp đầu ra. 
 trọng số đã cập nhật và chu trình tính lặp theo 4 
 Sai số này sẽ được lan truyền ngược về lớp bước nêu trên được thực hiện cho đến khi giá trị 
ẩn và trọng số được cập nhật theo công thức: sai số nhỏ hơn ngưỡng mong muốn, thường rất 
 ∆푊푖푗 = η휀푗 푖 (14) bé xấp xỉ 0. 
 +1 
 푊푖푗 = 푊푖푗 + Δ푊푖푗 + 훼훿푊푖푗 (15) 
 trong đó 3. Thực nghiệm 
 ∆푊 là số cải chính của 푊 ; 
 푖푗 푖푗 3.1. Giới thiệu dữ liệu thực nghiệm 
 η 0.01 là tỷ số huấn luyện; 
 푊 +1 là trọng số mới được sử dụng trong Đập thủy điện Hoà Bình nằm trên sông Đà ở 
 푖푗 20048’30” vĩ độ Bắc và 105019’26” kinh độ 
vòng huấn luyện thứ k+1; 
 Đông, được khởi công vào tháng 11/1979 và 
 푊푖푗 và Δ푊푖푗 lần lượt là trọng số và số cải hoàn thành tháng 12/1994. Đây là đập đá đổ lõi 
chính trong vòng huấn luyện thứ k; đất có chiều dài 970m và chiều cao 128m, bề 
 0.9 là hệ số động lượng sử dụng để giảm rộng mặt đập 20m tạo ra hồ chứa có dung tích 
xu hướng bất ổn [13]; thiết kế khoảng 9 tỷ mét khối, với công suất phát 
 điện thiết kế là 1920MW/năm. 
 W là sự thay đổi của số cải chính: Hệ thống quan trắc chuyển dịch ngang của 
 −1
 훿푊푖푗 = Δ푊푖푗 − Δ푊푖푗 (16) đập bố trí thành 2 tuyến ở mái hạ lưu tại độ cao 
 75m (6 điểm) và 123m (11 điểm). Dịch chuyển 
 2.3.3. Lan truyền ngược ở lớp ẩn 
 của các điểm này được theo dõi hàng tháng bằng 
 Bước này tính sai số của nơ-ron trong lớp ẩn phương pháp trắc địa. 
phức tạp hơn: 
 푛
 휀푖 = 푖(1 − 푖) ∑푗=1 푊푖푗휀푗 (17) 
 trong đó: 
 휀푖 và 푖 tương ứng là sai số và giá trị của nơ-
ron i trong lớp ẩn; 
 휀푗 là sai số của nơ-ron trong lớp đầu ra j có 
kết nối với nơ-ron i; 
 푊푖푗 là trọng số cập nhật của kết nối từ nơ-ron 
i đến nơ-ron j. 
 Khi các sai số này đã được xác định theo 
công thức (17), các số cải chính trọng số và trọng 
số mới giữa nơ-ron trong lớp đầu vào và nơ-ron Hình 2. Đập thủy điện Hoà Bình. 
 B.T.K. Trinh et al. / VNU Journal of Science: Earth and Environmental Sciences, Vol. 37, No. 1 (2021) 44-51 49 
 푡 và ̂푡 lần lượt là giá trị tính được từ mô 
 hình và giá trị quan trắc chuyển dịch ngang 
 tương ứng. 
 3.2. Các mô hình phân tích dự báo 
 3.2.1. Mô hình hồi quy bội 
 Hình 3. Sơ đồ bố trí mốc quan trắc. Áp dụng công thức (1) với i = 3, j = {1, 15, 
 30, 60}, các hệ số của mô hình hồi quy được xác 
 định theo phương pháp số bình phương nhỏ nhất. 
 Kết quả thu được: 
 훿(푡) = −7.66 10−2 + 9.39 10−4 −
 −8 3 −5
 2.16 10 + 9.97 10 1 +
 −4 −5
 1.96 10 30 − 7.40 10 60 −
 8.12 10−3√푡 + 1.27 10−2 ln 푡 (20) 
 Kết quả dự báo và đánh giá độ chính xác của 
 mô hình (20) được trình bày trong Hình 5 và 
 Bảng 1. 
 3.2.2. Mô hình SARIMA 
 Từ Hình 3 có thể thấy chuỗi giá trị chuyển 
 dịch ngang có xu thế tăng theo thời gian với quy 
 luật biến đổi mang tính chu kỳ tương ứng với 
 Hình 4. Dữ liệu thực nghiệm. biến động mực nước hồ và nhiệt độ không khí 
 hàng năm, do vậy chọn s = 12. 
 Trong nghiên cứu này, bộ dữ liệu quan trắc 
 Áp dụng kiểm định ADF với chuỗi dữ liệu 
chuyển dịch ngang của điểm M12 nằm ở giữa quan trắc chuyển dịch ngang ta thấy chuỗi sai 
đập là nơi có chuyển dịch lớn nhất, nhiệt độ phân bậc 1 là chuỗi ổn định, vậy d = 1. 
không khí trung bình tháng, và mực nước hồ tại Lập hàm ACF và PACF để xác định bậc cho 
137 chu kỳ quan trắc, từ tháng 9/1999 đến tháng mô hình MA và AR, kết quả p = 1 và q = 1. 
12/2010, được sử dụng để thiết lập các mô hình 
 Tổ hợp các giá trị p={0, 1}, d = 1, q={0, 1} 
phân tích, dự báo (Hình 4). với điều kiện p và q không đồng thời bằng 0 thu 
 Các mô hình đã thiết lập sẽ được sử dụng để 
 được 3 mô hình SARIMA(0,1,1) , 
dự báo ngắn hạn chuyển dịch của đập trong 4 12
 SARIMA(1,1,0) , SARIMA(1,1,1) đều là 
tháng, 6 tháng, 9 tháng và 12 tháng tiếp theo 12 12
 nhiễu trắng. Trong số này, mô hình 
nhằm đánh giá khả năng ứng dụng trong thực tế. 
 SARIMA(1,1,1) có giá trị AIC nhỏ nhất nên 
 Độ chính xác của các mô hình MTR, 12
 được chọn là mô hình tối ưu với công thức như sau: 
SARIMA và BPNN được đánh giá thông qua sai 
 (1 − 0.465B)(1 − 0.497B12)(1 − B)(1 −
số trung phương RMSE (Root Mean Square 12 12
 B )푌푡 = (1 + 0.566B)(1 + 0.996B )푒푡 (21) 
Error) và sai số trung bình MAE (Mean Absolute trong đó B là toán tử dịch chuyển lùi được 
Error): định nghĩa: 
 ∑ ( − ̂ )2
 푅 푆 = √ 푡=1 푡 푡 (18) 푌푡 = 푌푡−1 (22) 
 Kết quả dự báo và đánh giá độ chính xác của 
 1
 = ∑ | − ̂ | (19) 
 푡=1 푡 푡 mô hình (21) cũng được liệt kê trong Hình 5 và 
 trong đó: Bảng 1. 
 N là số lượng giá trị dự báo; 
50 B.T.K. Trinh et al. / VNU Journal of Science: Earth and Environmental Sciences, Vol. 37, No. 1 (2021) 44-51 
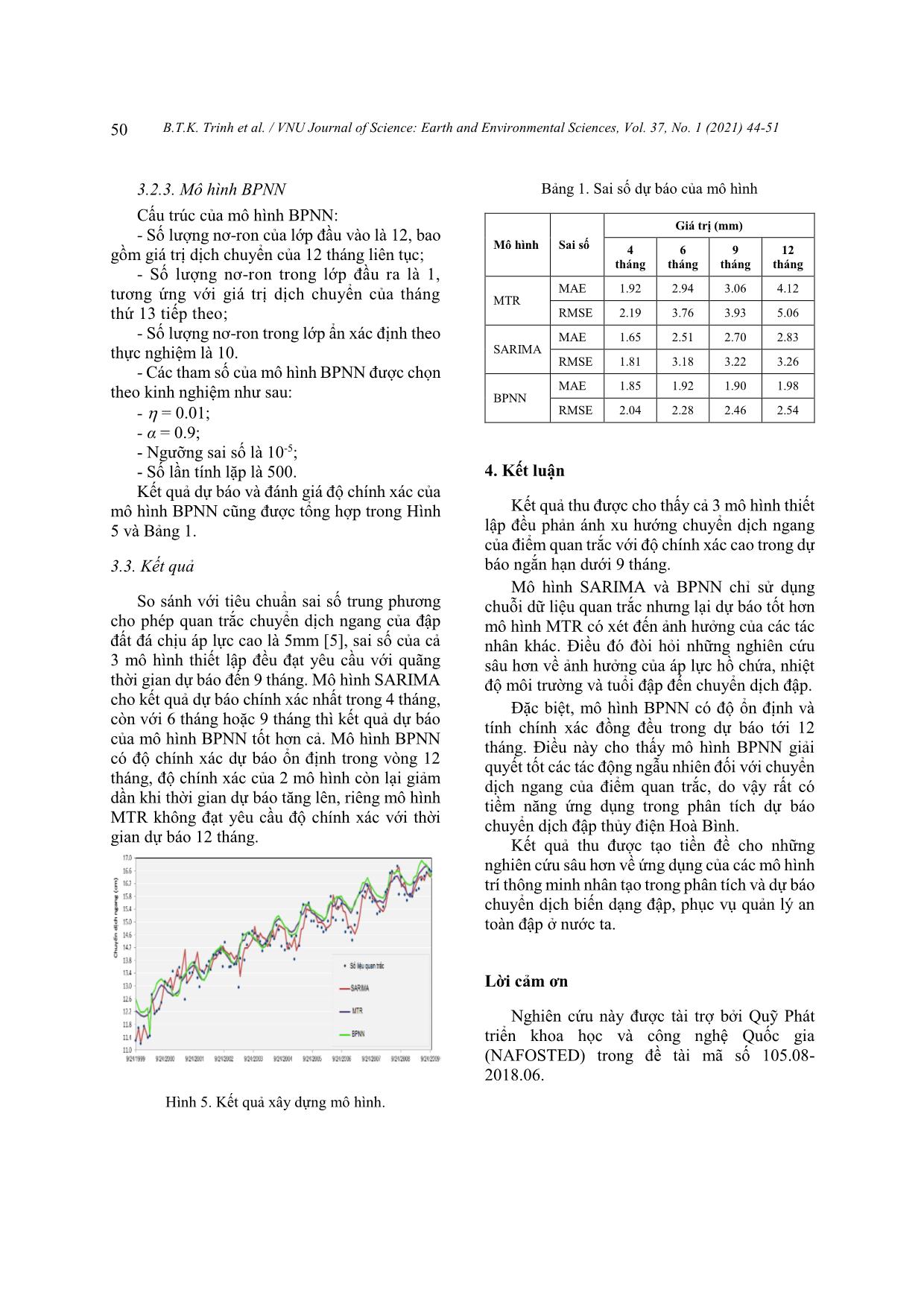
 3.2.3. Mô hình BPNN Bảng 1. Sai số dự báo của mô hình 
 Cấu trúc của mô hình BPNN: 
 Giá trị (mm) 
 - Số lượng nơ-ron của lớp đầu vào là 12, bao 
 Mô hình Sai số 
gồm giá trị dịch chuyển của 12 tháng liên tục; 4 6 9 12 
 tháng tháng tháng tháng 
 - Số lượng nơ-ron trong lớp đầu ra là 1, 
 MAE 1.92 2.94 3.06 4.12 
tương ứng với giá trị dịch chuyển của tháng MTR 
thứ 13 tiếp theo; RMSE 2.19 3.76 3.93 5.06 
 - Số lượng nơ-ron trong lớp ẩn xác định theo MAE 1.65 2.51 2.70 2.83 
thực nghiệm là 10. SARIMA 
 RMSE 1.81 3.18 3.22 3.26 
 - Các tham số của mô hình BPNN được chọn 
 MAE 1.85 1.92 1.90 1.98 
theo kinh nghiệm như sau: BPNN 
 -  = 0.01; RMSE 2.04 2.28 2.46 2.54 
 - α = 0.9; 
 - Ngưỡng sai số là 10-5; 
 - Số lần tính lặp là 500. 4. Kết luận 
 Kết quả dự báo và đánh giá độ chính xác của 
mô hình BPNN cũng được tổng hợp trong Hình Kết quả thu được cho thấy cả 3 mô hình thiết 
5 và Bảng 1. lập đều phản ánh xu hướng chuyển dịch ngang 
 của điểm quan trắc với độ chính xác cao trong dự 
3.3. Kết quả báo ngắn hạn dưới 9 tháng. 
 Mô hình SARIMA và BPNN chỉ sử dụng 
 So sánh với tiêu chuẩn sai số trung phương chuỗi dữ liệu quan trắc nhưng lại dự báo tốt hơn 
cho phép quan trắc chuyển dịch ngang của đập mô hình MTR có xét đến ảnh hưởng của các tác 
đất đá chịu áp lực cao là 5mm [5], sai số của cả nhân khác. Điều đó đòi hỏi những nghiên cứu 
3 mô hình thiết lập đều đạt yêu cầu với quãng sâu hơn về ảnh hưởng của áp lực hồ chứa, nhiệt 
thời gian dự báo đến 9 tháng. Mô hình SARIMA độ môi trường và tuổi đập đến chuyển dịch đập. 
cho kết quả dự báo chính xác nhất trong 4 tháng, 
 Đặc biệt, mô hình BPNN có độ ổn định và 
còn với 6 tháng hoặc 9 tháng thì kết quả dự báo 
 tính chính xác đồng đều trong dự báo tới 12 
của mô hình BPNN tốt hơn cả. Mô hình BPNN 
 tháng. Điều này cho thấy mô hình BPNN giải 
có độ chính xác dự báo ổn định trong vòng 12 
 quyết tốt các tác động ngẫu nhiên đối với chuyển 
tháng, độ chính xác của 2 mô hình còn lại giảm 
 dịch ngang của điểm quan trắc, do vậy rất có 
dần khi thời gian dự báo tăng lên, riêng mô hình 
 tiềm năng ứng dụng trong phân tích dự báo 
MTR không đạt yêu cầu độ chính xác với thời 
 chuyển dịch đập thủy điện Hoà Bình. 
gian dự báo 12 tháng. 
 Kết quả thu được tạo tiền đề cho những 
 nghiên cứu sâu hơn về ứng dụng của các mô hình 
 trí thông minh nhân tạo trong phân tích và dự báo 
 chuyển dịch biến dạng đập, phục vụ quản lý an 
 toàn đập ở nước ta. 
 Lời cảm ơn 
 Nghiên cứu này được tài trợ bởi Quỹ Phát 
 triển khoa học và công nghệ Quốc gia 
 (NAFOSTED) trong đề tài mã số 105.08-
 2018.06. 
 Hình 5. Kết quả xây dựng mô hình. 
 B.T.K. Trinh et al. / VNU Journal of Science: Earth and Environmental Sciences, Vol. 37, No. 1 (2021) 44-51 51 
Tài liệu tham khảo [6] Ministry of Science and Technology of Vietnam, 
 TCVN 8215-2009: Hydraulic Structure – Major 
 [1] B.T.K. Trinh et al., A novel hybrid artificial regulations on installation design observation 
 intelligent approach based on neural fuzzy equipment of water headworks, 2009 (in 
 inference model and particle swarm optimization Vietnamese). 
 for horizontal displacement modeling of [7] Ministry of Science and Technology of Vietnam, 
 hydropower dam, Neural Computing and TCVN 9360-2012: Technical Process of 
 Applications 29(12) (2018) 1495-1506. Settlement Monitoring of Civil and Industrial 
 https://doi.org/10.1007/s00521-016-2666-0 Building by Geometrical Levelling, 2012 (in 
 [2] Z. Jingui et al., Research on Deformation Analysis Vietnamese). 
 of the Hydropower Dam in Vietnam, Journal of [8] Ministry of Science and Technology of Vietnam, 
 Geomatics - Wuhan University. 41(3) (2016) 45- TCVN 9400-2012: Buildings and Tower Structure 
 47 (in Chinese). https://doi.org/10.14188/j.2095- –Tilt Monitoring by Surveying Methods, 2012 (in 
 6045.2016.03.012 Vietnamese). 
 [3] D.T. Bui et al., Chapter 15 - Hybrid Intelligent [9] T. Khanh and L.D. Tinh, Applying a method of 
 Model Based on Least Squared Support Vector correlation analysis to estimate the movement of 
 Regression and Artificial Bee Colony Optimization construction, Journal of Mining and Geology 4, 30 
 for Time Series Modeling and Forecasting (2010) (in Vietnamese). 
 Horizontal Displacement of Hydropower Dam, in: [10] L D. Tinh, Research the solutions to Increase the 
 P. Samui, S.S. Roy, and V.E. Balas (Eds.), Effect of Deformation Monitoring in Vietnam 
 Handbook of Neural Computation, Academic (PhD thesis), Hanoi University of Mining and 
 Press, United States of America, 2017, pp 279-293, Geology, MS: 62.52.85.01, 2012 (in Vietnamese). 
 https://doi.org/10.1016/B978-0-12-811318-
 [11] J.D. Cryer, K.S. Chan, Time Series Analysis with 
 9.00015-6 
 Application in R, Springer-Verlag, New York, 2008. 
 [4] J. Zou et al., Dam deformation analysis based on 
 [12] N.Q. Dong, N.T. Minh, Econometric, The Press of 
 BPNN merging models, Geo-spatial Information 
 National Economics University, 2013 (in 
 Science, 21(2) (2017) 49-157. 
 Vietnamese). 
 https://doi.org/10.1080/10095020.2017.1386848 
 [13] D. Graupe, Principles of Artifcial Neural Networks, 
 [5] Ministry of Science and Technology of Vietnam, 
 Advanced Series in Circuits and Systems 3rd Edition, 
 TCVN 9399-2012: Buildings and Structures – 
 vol. 7, World Scientific Publishing Co. Pte. Ltd., 
 Measuring Horizontal Displacement by Surveying 
 Singapore, 311–325, 2013. 
 Method, 2012 (in Vietnamese).