Tối ưu hóa thiết kế bộ MTMD giảm dao động xoắn cho trục ứng dụng thuật toán hồi quy phi tuyến Gauss-Newton

ISSN 2354-0575
 TỐI ƯU HÓA THIẾT KẾ BỘ MTMD GIẢM DAO ĐỘNG XOẮN CHO TRỤC
 ỨNG DỤNG THUẬT TOÁN HỒI QUY PHI TUYẾN GAUSS-NEWTON 
 Khổng Doãn Điền1, Nguyễn Duy Chinh1, Vũ Xuân Trường1, Nguyễn Thanh Tuấn2
 1 Trường Đại học Sư phạm Kỹ thuật Hưng Yên
 2 Trường Cao đẳng nghề Công nghiệp Thanh Hóa
 Ngày nhận: 06/4/2016
 Ngày sửa chữa: 11/5/2016
 Ngày xét duyệt: 10/6/2016
Tóm tắt:
 Các công bố [3,4] đã đưa ra được vùng tối ưu của các tham số bộ TMD. Tuy nhiên vì mỗi biến chỉ 
có hữu hạn các cấp độ được chọn (3 đến 4 cấp độ) trong vùng khảo sát, do đó bộ thông số tối ưu thu được 
là một trong các giá trị của các cấp độ trong vùng tối ưu đã chọn. Taguchi không trả ra hàm mô tả quan 
hệ giữa các đại lượng đầu vào và đại lượng khảo sát mà đánh giá tối ưu thông số tỷ số tín hiệu trên nhiễu 
(S/N). Bài báo này phân tích hiệu quả giảm dao động khi sử dụng đồng thời nhiều bộ TMD (MTMD-Multi 
Tuned Mass Damper). Đặc biệt phương pháp tối ưu hóa sử dụng trong nghiên cứu này là phương pháp hồi 
quy phi tuyến Gauss-Newton, kết quả sẽ đánh giá được quan hệ giữa các thông số MTMD với dao động 
xoắn thông qua một hàm toán học dạng phi tuyến. Các kết quả được kiểm chứng bằng mô phỏng số trên 
Maple 2016a cho kết quả tin cậy.
Từ khóa: Hồi quy phi tuyến, Thuật toán Gauss-Newton, MTMD.
1. Cơ sở lý thuyết Nếu m = n, vòng lặp rút gọn
 (s+1) (s) -1 (s)
 Các thuật toán Gauss-Newton được sử dụng β = β - (Jr) r(β )
để giải quyết các bài toán bình phương tối thiểu Đó là một sự tổng quát trực tiếp của phương 
các hàm phi tuyến tính. Thuật toán này được Carl pháp Newton trong một chiều.
Friedrich Gauss cài tiến từ phương pháp Newton Khi phù hợp dữ liệu để tìm các thông số β thì 
cho việc tìm giá trị nhỏ nhất của hàm. Không giống hàm mẫu đã cho y = f(x, β) sẽ phù hợp nhất một số 
như các phương pháp của Newton, các thuật toán điểm dữ liệu (xi, yi), hàm ri là hàm dư thừa
Gauss-Newton chỉ có thể được sử dụng để giảm rybb=-fx,
 ii_ i i
thiểu một tổng các giá trị hàm bình phương, nhưng Sau đó, các phương pháp_ Gauss-Newtoni có 
nó có thuận lợi là các đạo hàm bậc hai không được thể được thể hiện trong điều khoản của Jacobi Jf 
yêu cầu tính cũng có thể được tính. Bài toán bình của hàm f là 
 (s+1) (s) T -1 T (s)
phương tối thiểu phi tuyến tính có thể nảy sinh β = β - (Jr Jf) Jr r(β )
trong hồi qui phi tuyến, khi các tham số trong mô Việc giả sử m ≥ n trong thuật toán là cần 
 T
hình hồi qui được tìm thấy thì mô hình phù hợp với thiết, vì nếu không ma trận Jr Jr không thể nghịch 
những quan sát có sẵn. Nội dung chính của phương đảo được và các phương trình bình thường không 
pháp này như sau: thể được giải quyết (ít nhất và duy nhất).
 Cho m hàm r = (r1, ..., rm) (thường được gọi là Các thuật toán Gauss-Newton có thể được 
dư) của n biến β = (β1, ..., βn), với m ≥ n, thuật toán bắt nguồn bởi vector xấp xỉ tuyến tính của hàm ri. 
Gauss-Newton tìm các giá trị của các biến một cách Sử dụng định lý của Taylor, chúng ta có thể viết ở 
lặp đi lặp lại để làm tối thiểu tổng bình phương [1] mỗi lần lặp
 m s s
 2 rrbb. + Jr b D
 S(bb) = / ri _ i __ii
 i = 1 _i Với D =-bbs . Nhiệm vụ tìm Δ để tối thiểu 
 Bắt đầu với b()0 để tối thiểu, phương pháp tổng bình phương của phía bên tay phải, tức là,
 s s < 2
tiến hành các vòng lặp min||r(β )+Jr(β )Δ 2
 (s+1) (s) T -1 T (s)
 β = β - (Jr Jr) Jr r(β ) là một bài toán bình phương tối thiểu tuyến tính 
 Nếu r và β là vector cột, các mục của các ma có thể được giải một cách dễ dàng, thu được các 
trận Jacobian là phương trình bình thường trong thuật toán.
 s
 2ri b
 (J ) = _i 2. Phương trình vi phân dao động xoắn của cơ hệ
 r ij 2b
 j Xét mô hình trục máy có lắp MTMD như 
và biểu tượng T biểu thị sự chuyển vị ma trận. Hình 1. Trên trục máy có lắp đĩa khối lượng mr, bán 
14 Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology
 ISSN 2354-0575
kính Rr. MTMD được lắp đối xứng qua tâm đĩa máy Vậy phương trình vi phân chuyển động của 
trên đường tròn bán kính e (Hình 2). Trục máy quay cơ hệ: 
 4
đều với tốc độ n vòng/phút. 2
 Jmri{{pp++ek/ {{p =- s -+XtM()t ( 4 ) 
 i = 1 _i 
 222
 me {{pp+=iimgeksin {{--eciie {o
 _i 
 (.i = 14.) (5)
 3. Xác định tham số tối ưu của MTMD bằng 
 thuật toán Gauss-Newton
 Ta đặt các hệ số hằng :
 m k c
 na==;;b =
 M kttk 
 Sử dụng vùng khảo sát tối ưu của các biến 
 khảo sát như đã được công bố trong [3,4]. Các cấp 
 độ được chọn trong vùng tối ưu được mô tả trên 
 Hình 1. Mô hình trục máy có lắp MTMD Bảng 1. Bảng thực nghiệm L9 được chọn như trên 
 Bảng 2. Bảng 3 mô tả kết quả thu được khi mô 
 phỏng số dao động xoắn của trục lắp MTMD trên 
 phần mềm Maple 2016a.
 Bảng 1. Miền khảo sát và cấp độ của các thông số 
 khảo sát
 Cấp độ n a β
 1 0.01 0.05 0.001
 2 0.02 0.10 0.005
 3 0.03 0.15 0.010
 Bảng 2. Bảng thực nghiệm L9
 Cấp độ n a β
 Hình 2. Mô hình MTMD 1 1 1 1
 2 1 2 2
 Động năng của cơ hệ 3 1 3 3
 1 221 1 22
TJ=+X Jm{{oo+=ei(.14.)
 2 sr2 2 i ( 1 ) 4 2 1 2
 Tính thế năng của cơ hệ 5 2 2 3
 4 4
 1 221 2
PX=+mgek//cos({{i eki +-s { tt) 6 2 3 1
 i ==1 2 i 1 2 _i
 (2) 7 3 1 3
 Hàm hao tán: 
 4 8 3 2 1
 1 22
 U = ce / {o i (3) 9 3 3 2
 2 i = 1
 Bảng 3. Bảng thực nghiệm khi chạy mô phỏng trên Maple 2016
 Bộ n # 4% a # 10% b # 1% Dao động xoắn tại t = 1s
 1 0.01 0.05 0.001 0.00749396853866408
 2 0.01 0.10 0.005 0.02697986205450190
 3 0.01 0.15 0.010 0.04412186472455790
 4 0.02 0.05 0.005 0.00957495705958608
 5 0.02 0.10 0.010 0.02673585648017400
 6 0.02 0.15 0.001 0.00521742659631808
 7 0.03 0.05 0.010 0.00635671647822808
Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology 15
ISSN 2354-0575
 8 0.03 0.10 0.001 0.00521739126929808
 9 0.03 0.05 0.001 0.00521739132449408
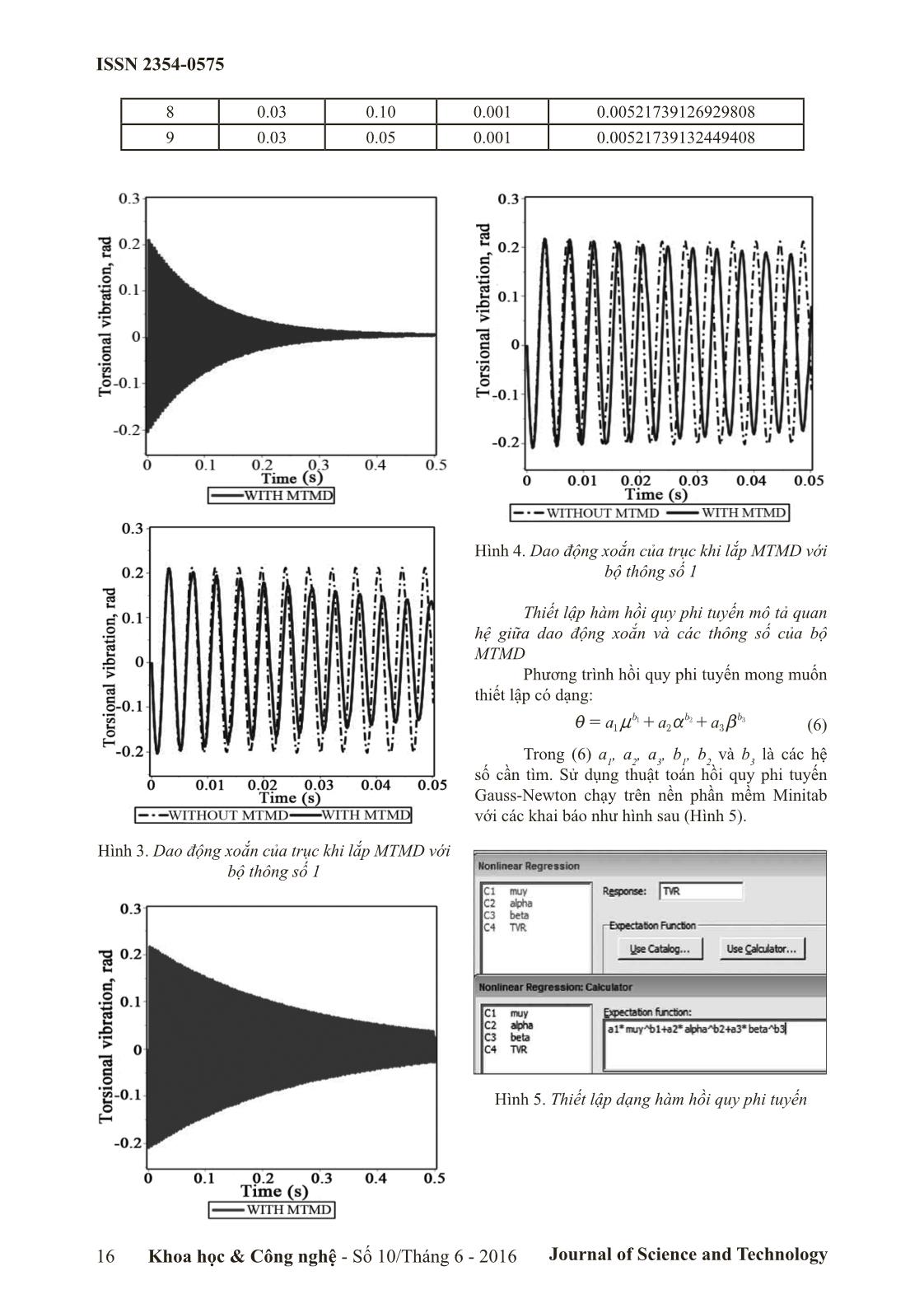
 Hình 4. Dao động xoắn của trục khi lắp MTMD với 
 bộ thông số 1
 Thiết lập hàm hồi quy phi tuyến mô tả quan 
 hệ giữa dao động xoắn và các thông số của bộ 
 MTMD
 Phương trình hồi quy phi tuyến mong muốn 
 thiết lập có dạng:
 in=+aabb12ab+ a b3
 123 (6)
 Trong (6) a1, a2, a3, b1, b2 và b3 là các hệ 
 số cần tìm. Sử dụng thuật toán hồi quy phi tuyến 
 Gauss-Newton chạy trên nền phần mềm Minitab 
 với các khai báo như hình sau (Hình 5).
Hình 3. Dao động xoắn của trục khi lắp MTMD với 
 bộ thông số 1
 Hình 5. Thiết lập dạng hàm hồi quy phi tuyến
16 Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology
 ISSN 2354-0575
 Ta thu được các kết quả tính toán
 20
4. Kết quả và nhận xét theta:.=+1 86522 $ 1023 . n5.75995$10
 Như vậy, phương trình phi tuyến mô tả dao 
 ++$$ab-0..0288234 0 52258
động xoắn của trục (Hình 1) khi lắp MTMD với các 0 ..00279629 0 216406
thông số khảo sát là: with(Optimization):
 20 1 3 5 15
 23 5..75995 10 -0.0288234 n = a =
in=+1 ..86522 10 0 . 00279629a + NLPSolve(theta, 100 ..100 , 100 ..100 , 
 1 1
 0.52258 b =
+0 . 216406b (7) 1000 ..100 );
 Về mặt toán học khi hàm đã xác định hoàn Kết quả thu được như sau:
toàn cho chúng ta dự đoán về dao động xoắn với nopt ==00.%33 
các thông số đầu vào đã cho. Nghĩa là với mỗi bộ aopt ==01.%515
thông số thiết kế cho ta một dự đoán xấp xỉ về dao bopt ==0 ..0009999 0 099 %
động xoắn. Và cũng từ hàm phi tuyến này cho phép 
chúng ta tìm được cực trị của hàm để xác định các 
tham số tối ưu.
 Để đánh giá độ tin cậy của hàm hồi quy phi 
tuyến thu được từ đại lượng SSE mục Summary. 
Đại lượng này có nghĩa là tổng bình phương các lỗi 
còn sót lại (the sum of squares of the residual error). 
SSE = 0.0009495 = 0.09495%. Kết quả này mô tả 
phương trình hồi quy phi tuyến thu được ở trên là 
rất tin cậy. 
 Tiếp theo tác giả xác định tham số tối ưu 
của hàm phi tuyến. Chương trình được lập trên 
Maple 2016a bằng việc sử dụng thư viện tối ưu hóa 
Optimization và lệnh NLPSolve để tìm cực tiểu của 
hàm phi tuyến.
Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology 17
ISSN 2354-0575
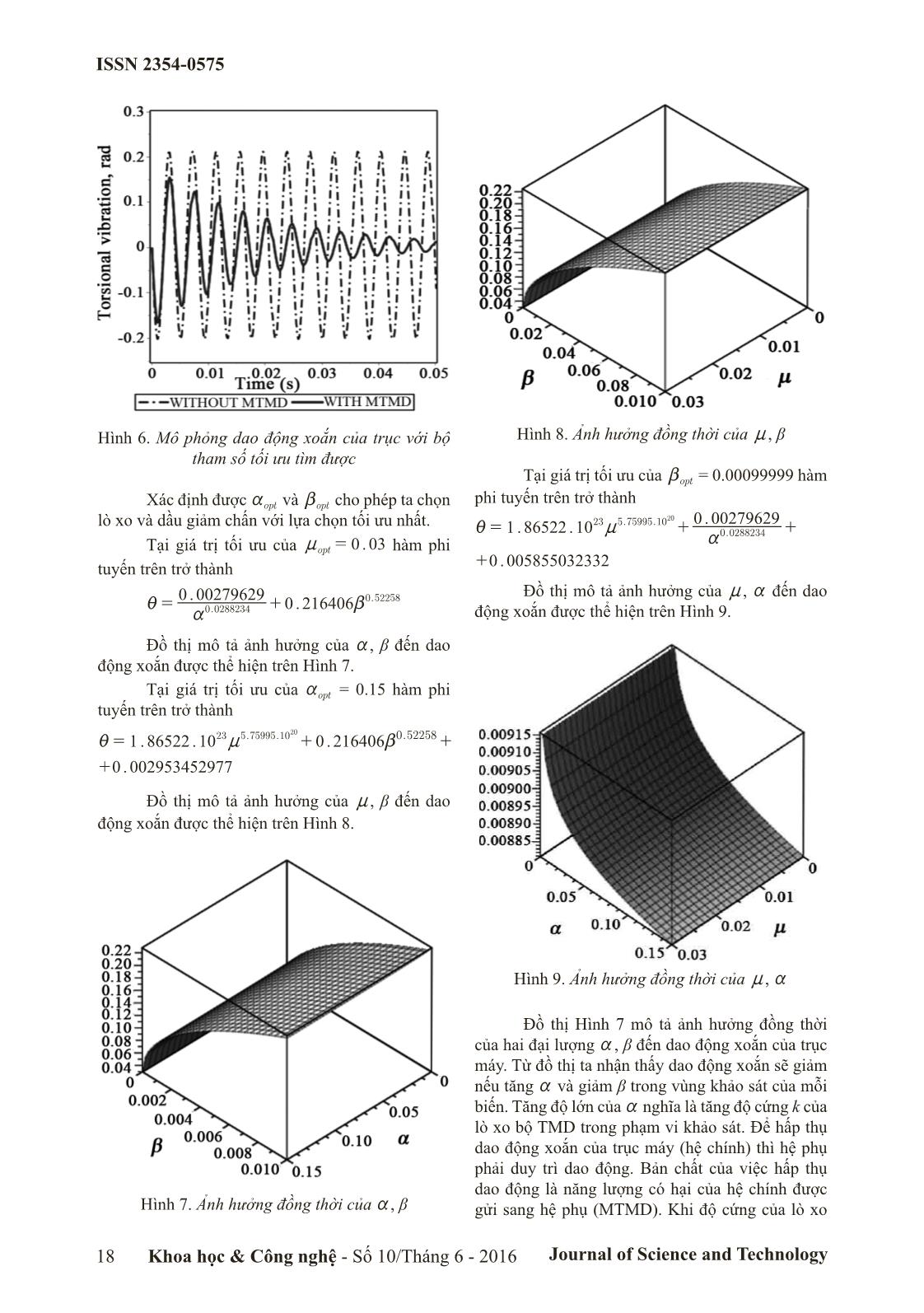
Hình 6. Mô phỏng dao động xoắn của trục với bộ Hình 8. Ảnh hưởng đồng thời của n, β
 tham số tối ưu tìm được
 Tại giá trị tối ưu của bopt = 0.00099999 hàm 
 Xác định được aopt và bopt cho phép ta chọn phi tuyến trên trở thành
 23 5..75995 1020 0 . 00279629
lò xo và dầu giảm chấn với lựa chọn tối ưu nhất. in=+1 ..86522 10 +
 a0.0288234
 Tại giá trị tối ưu của nopt = 00. 3 hàm phi 
 +
tuyến trên trở thành 0 . 005855032332
 0 . 00279629 0.52258 Đồ thị mô tả ảnh hưởng của n, a đến dao 
 i =+0 . 216406b
 a0.0288234 động xoắn được thể hiện trên Hình 9.
 Đồ thị mô tả ảnh hưởng của a, β đến dao 
động xoắn được thể hiện trên Hình 7.
 Tại giá trị tối ưu của aopt = 0.15 hàm phi 
tuyến trên trở thành
 20
in=+1 ..86522 1023 5..75995 10 0 . 216406b0.52258 +
+0 . 002953452977
 Đồ thị mô tả ảnh hưởng của n, β đến dao 
động xoắn được thể hiện trên Hình 8.
 Hình 9. Ảnh hưởng đồng thời của n, a
 Đồ thị Hình 7 mô tả ảnh hưởng đồng thời 
 của hai đại lượng a , β đến dao động xoắn của trục 
 máy. Từ đồ thị ta nhận thấy dao động xoắn sẽ giảm 
 nếu tăng a và giảm β trong vùng khảo sát của mỗi 
 biến. Tăng độ lớn của a nghĩa là tăng độ cứng k của 
 lò xo bộ TMD trong phạm vi khảo sát. Để hấp thụ 
 dao động xoắn của trục máy (hệ chính) thì hệ phụ 
 phải duy trì dao động. Bản chất của việc hấp thụ 
 dao động là năng lượng có hại của hệ chính được 
 Hình 7. Ảnh hưởng đồng thời của a, β gửi sang hệ phụ (MTMD). Khi độ cứng của lò xo 
18 Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology
 ISSN 2354-0575
đủ lớn sẽ dễ dàng duy trì dao động của hệ phụ để nghĩa là sự thay đổi sự các biến đầu vào a, β làm 
hấp thụ năng lượng có hại của hệ chính. Tuy nhiên, dao động xoắn của hệ tăng hoặc giảm nhanh. Kết 
mặt cong biểu diễn mối quan hệ này là mặt cong lồi, quả thu được tương tự trên các đồ thị Hình 8 và 9.
Tài liệu tham khảo
 [1]. Nguyễn Thúc An, Nguyễn Đình Chiều, Khổng Doãn Điền, Lý thuyết dao động, NXB nông 
 nghiệp, 2004.
 [2]. Nguyễn Văn Khang, Dao động kỹ thuật, NXB khoa học kỹ thuật, Hà Nội 2009.
 [3]. Khổng Doãn Điền, Nguyễn Duy Chinh, Vũ Xuân Trường, Nguyễn Ngọc Chung, Nghiên cứu xác 
 định tham số tối ưu của bộ hấp thụ dao động TMD dạng con lắc kép giảm dao động xoắn cho trục 
 máy, Tạp chí Khoa học và Công nghệ, ISSN 2354-0575, Vol6 (6/2015).
 [4]. Khổng Doãn Điền, Nguyễn Duy Chinh, Vũ Xuân Trường, Đoàn Cao Miên, Tối ưu hóa thông 
 số bộ hấp thụ dao động TMD dạng rãnh trượt tròn giảm dao động xoắn cho trục máy bằng phương 
 pháp Euler, Tạp chí Khoa học và Công nghệ, ISSN 2354-0575, Vol6 (6/2015).
 [5]. H. O. Hartley, The Modified Gauss-Newton Method for the Fitting of Non-Linear Regression 
 Functions by Least Squares, Technometrics, Volume 3, DOI:10.1080/00401706.1961.10489945.
 [6]. Jorge J. Moré, The Levenberg-Marquardt Algorithm: Implementation and Theory, 
 ChapterNumerical Analysis, Volume 630 of the series Lecture Notes in Mathematics, pp 105-116.
 OPTIMAL DESIGN OF THE MTMD FOR REDUCING TORSIONAL VIBRATION
 BY USING GAUSS-NEWTON NONLINEAR REGRESSION ALGORITHM
Abtract:
 The published in [3,4] have determined the optimal parameters range for the TMD. However, as 
each factors were only limited to the selected level (level 3 to 4) in the survey, so the optimal parameters 
obtained is one of the values of the optimal regional level. The Taguchi method does not return the results in 
the form of mathematical functionsthat the optimal parameters were determined by the S/N ratio. This paper 
presents effectively reduce torsional vibration when using MTMD. Specially, the optimization methods used 
in this study is the method of Gauss-Newton nonlinear regression algorithm. Results will be shown the 
relationship between these parameters to MTMD by a nonlinear mathematical function form. The results 
are verified by numerical simulation on Maple 2016a.
Keywords: Nonlinear Regression, Gauss-Newton algorithm, Multi Tuned Mass Dampers.
Khoa học & Công nghệ - Số 10/Tháng 6 - 2016 Journal of Science and Technology 19