Tốc độ rã tự phát và độ dịch mức năng lượng của một nguyên tử hai mức khi có mặt khối trụ vật chất nhiều lớp

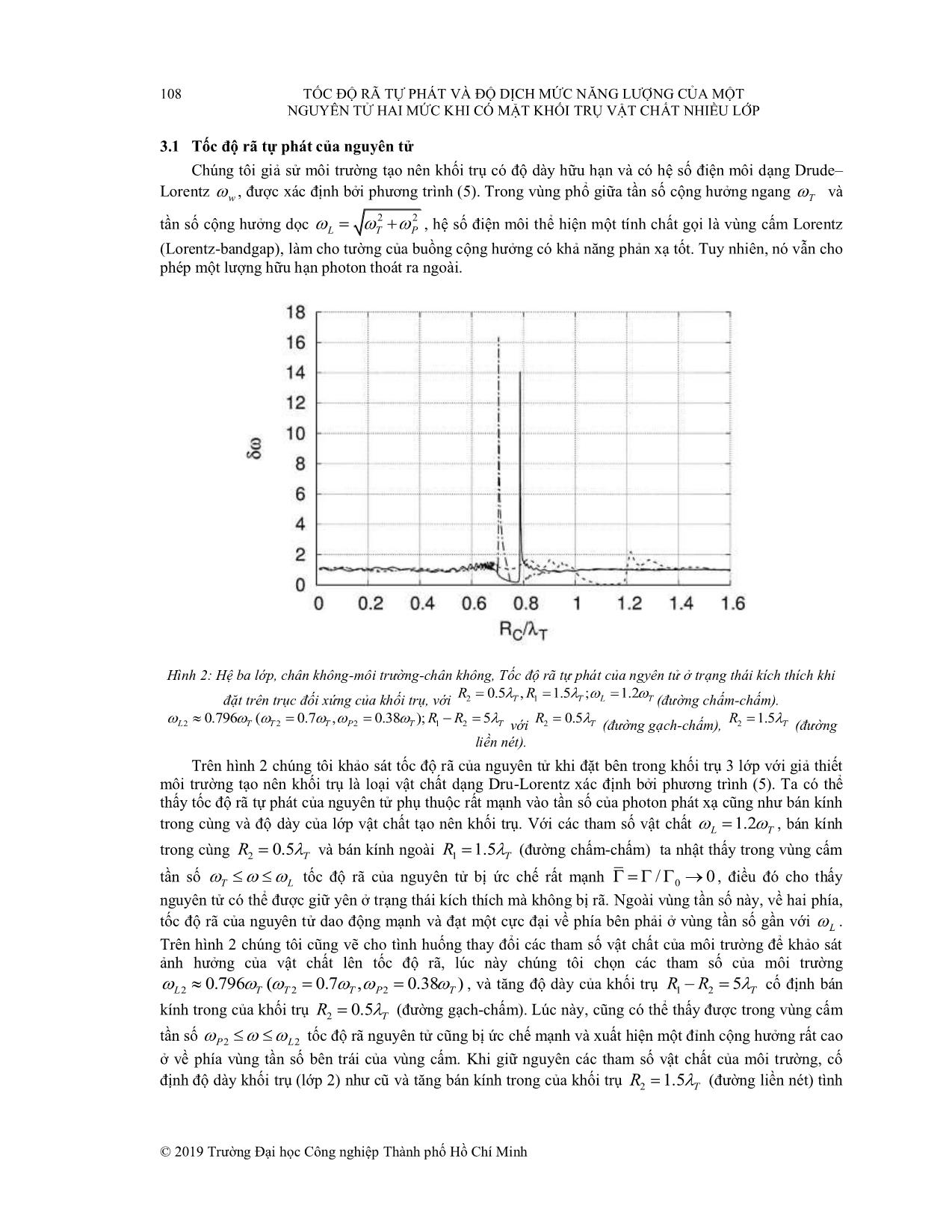
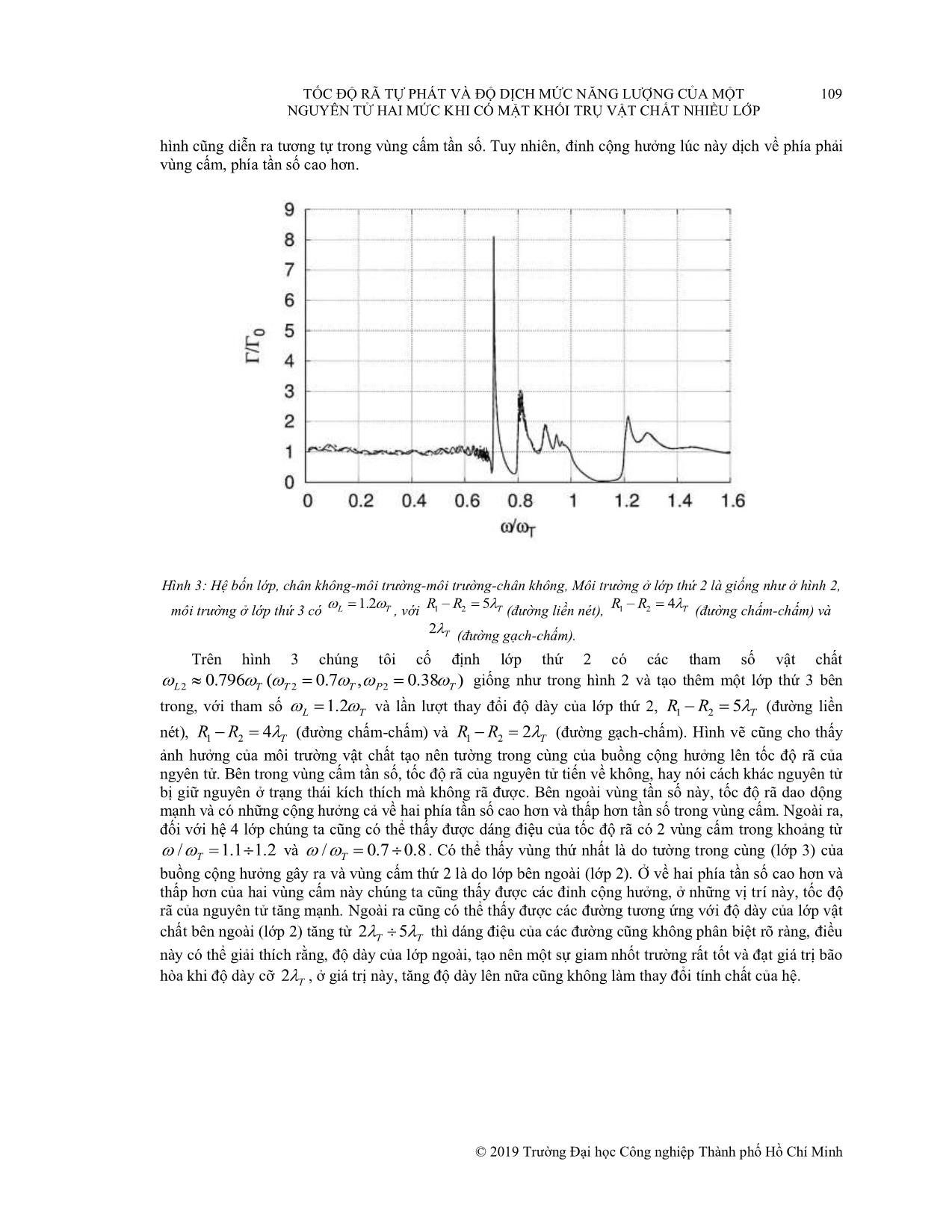
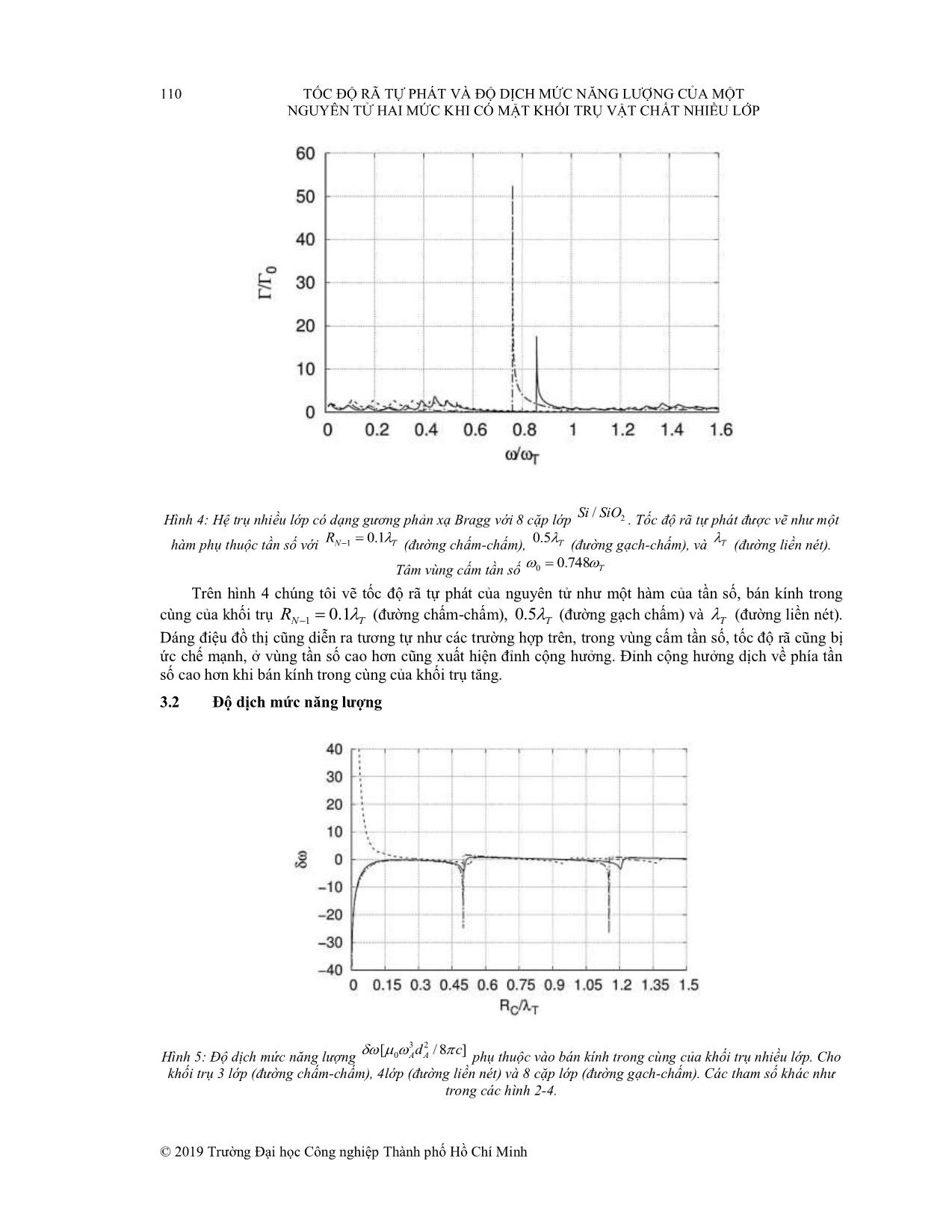
Tạp chí Khoa học và Công nghệ, Số 40, 2019 
 TỐC ĐỘ RÃ TỰ PHÁT VÀ ĐỘ DỊCH MỨC NĂNG LƯỢNG CỦA MỘT 
 NGUYÊN TỬ HAI MỨC KHI CÓ MẶT KHỐI TRỤ VẬT CHẤT NHIỀU LỚP 
 TRẦN MINH HIẾN 
 Khoa Công nghệ Cơ khí, Trường Đại học Công nghiệp Tp. Hồ Chí Minh, 
 tranminhhien@iuh.edu.vn 
Tóm tắt. Chúng tôi khảo sát tốc độ rã tự phát của một nguyên tử hai mức bị kích thích được đặt trên trục 
đối xứng của một khối trụ điện môi phân lớp. Ba cấu hình được xem xét: khối trụ ba lớp và bốn lớp được 
tạo nên bởi chất điện môi dạng Drude-Lorentz, dạng vùng cấm-Lorentz, và dạng gương phản xạ Bragg. 
Kết quả cho thấy, nếu tần số chuyển mức nguyên tử, rơi vào vùng cấm của môi trường tạo nên các lớp 
của khối trụ, nguyên tử có thể bị giữ ở trạng thái kích thích. Bên cạnh đó, tốc độ rã được tăng cường rất 
mạnh ở vùng tần số về phía hai bên của vùng cấm. Dịch chuyển Lamb cũng được xem xét trong bài báo 
này. 
 SPONTANEOUS DECAY RATE AND LEVEL SHIFT OF A TWO-LEVEL ATOM IN THE 
 PRESENCE OF A MULTILAYERED-CYLINDRICAL WAVEGUIDE 
Abstract. We consider the spontaneous decay rate of a two-level excited atom positioned on axis of a 
multilayered-cylindrical waveguide. Three types of configuration are studied including a three-layer and a 
four-layer Drude-Lorentz type, Lorentz-bandgap type, and a Bragg-distributed mirror type. It is shown 
that if the atomic transition frequency falls within the bandgap of the medium filling the wall of the 
resonator, the atom can be trapped in the excited state. Besides, the decay rate is strongly enhanced near 
the edge of the bandgap. The Lamb shift is also considered. 
Keywords. Bragg-distributed mirror, Cylindrical waveguide, Lamb shift, Spontaneous decay. 
1 MỞ ĐẦU 
 Phát xạ tự phát là quá trình một nguồn như nguyên tử, phân tử, tinh thể nano hoặc ion ở trạng thái 
kích thích chuyển về mức năng lượng thấp hơn và phát ra một photon. Nếu mức kích thích có năng lượng 
 E2 và mức thấp hơn có năng lượng E1 thì photon phát ra sẽ có tần số ω và năng lượng tương ứng là  . 
Phát xạ tự phát là một quá trình cơ bản trong nhiều ứng dụng công nghệ như: ống huỳnh quang, màn hình 
TV (ống tia cathode), màn hình plasma, laser, kính hiển vi quét trường gần hay các khóa lượng tử .... 
Bằng cách thay đổi hình học và tính chất của môi trường vật chất bao quanh người ta có thể điều khiển 
tốc độ phát, thời điểm phát và hướng phát photon như mong muốn [1]. Đặt nguồn vào những môi trường 
thích hợp khác nhau cho ta những ứng dụng quan trọng trong quang học và quang điện tử. Ví dụ như các 
nguồn phát đơn photon, là loại nguồn sử dụng trong mã hóa lượng tử. Chỉ nguồn phát đơn photon mới 
cho phép độ bảo mật cao nhất vì trong quá trình phát xạ, mỗi lần chỉ một photon xuất hiện. Ngoài ra ta 
cũng có thể điều khiển khoảng cách thời gian giữa hai lần phát liên tiếp cũng như chọn tần số của photon. 
Từ năm 1946 với công trình đầu tiên của Purcell [2], người ta đã biết tốc độ phân rã trạng thái và dịch 
chuyển mức năng lượng của một hệ phân tử có thể thay đổi khi ta đặt nó trong một môi trường phù hợp. 
Như đã biết, quá trình rã tự phát đóng vai trò rất quan trọng trong các thiết bị quang tử. Người ta có thể 
điều khiển quá trình này bằng cách điều chỉnh môi trường xung quanh nguồn phát xạ. Các thuộc tính của 
quá trình rã có thể tìm hiểu thông qua khảo sát hàm Green [3, 4]. Các cấu trúc đối xứng trụ xuất hiện 
trong các nghiên cứu gần đây về atom chips [5], tốc độ rã tự phát và dịch chuyển mức [1, 6 – 12], năng 
lượng điểm không [13], tương tác Casimir-Polder [14 – 16] và sự truyền năng lượng cộng hưởng giữa các 
phân tử [17]. Trong các công trình này, hệ trụ được giả sử dài vô hạn. Bài toán tốc độ rã tự phát của 
nguyên tử đặt gần khối trụ hai lớp cũng đã được xem xét [18]. Ở đây chúng tôi sẽ xem xét bài toán về tốc 
© 2019 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
 TỐC ĐỘ RÃ TỰ PHÁT VÀ ĐỘ DỊCH MỨC NĂNG LƯỢNG CỦA MỘT 103 
 NGUYÊN TỬ HAI MỨC KHI CÓ MẶT KHỐI TRỤ VẬT CHẤT NHIỀU LỚP 
độ rã và sự dịch mức năng lượng của nguyên tử hai mức khi đặt bên trong khối trụ có cấu trúc nhiều lớp 
dài vô hạn. Hệ 3 lớp và 4 lớp cũng được xem xét. 
 Hình 1: Mô hình khối trụ nhiều lớp 
2 CÁC PHƯƠNG TRÌNH CƠ BẢN 
 Phát xạ tự phát là một ví dụ thể hiện rõ tác động của trạng thái chân không của trường điện từ lên các 
quá trinh vật lý có thể đo được. Einstein đã chỉ ra rằng, để thu được định luật bức xạ Planck, lý thuyết rã 
trạng thái của nguyên tử nhất thiết phải bao gồm cả quá trình phát xạ tự phát [19]. Các tính chất của hiện 
tượng bức xạ của một nguyên tử bị kích thích trong chân không đã được nghiên cứu một cách rộng rãi và 
tốc độ rã tự phát của một nguyên tử (hai mức) bị kích thích được cho bởi biểu thức 
 3 2
  Ad A
 0 3 , (1) 
 3 0c
trong đó  A A  là tần số chuyển mức đã bị dịch đi một lượng  , với  là dịch chuyển 
 ˆ ˆ
Lamb. d A là độ lớn của phần tử ma trận dAA ldu udl A của toán tử mô men lưỡng cực 
 ˆ
nguyên tử d A giữa trạng thái trên u và trạng thái dưới l và  ...  báo này đôi khi chúng tôi sẽ gọi hệ như là một buồng cộng hưởng, với lớp thứ N 1 là tường 
trong cùng của buồng cộng hưởng. 
 © 2019 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
108 TỐC ĐỘ RÃ TỰ PHÁT VÀ ĐỘ DỊCH MỨC NĂNG LƯỢNG CỦA MỘT 
 NGUYÊN TỬ HAI MỨC KHI CÓ MẶT KHỐI TRỤ VẬT CHẤT NHIỀU LỚP 
3.1 Tốc độ rã tự phát của nguyên tử 
 Chúng tôi giả sử môi trường tạo nên khối trụ có độ dày hữu hạn và có hệ số điện môi dạng Drude–
Lorentz w , được xác định bởi phương trình (5). Trong vùng phổ giữa tần số cộng hưởng ngang T và 
 2 2
tần số cộng hưởng dọc L  T P , hệ số điện môi thể hiện một tính chất gọi là vùng cấm Lorentz 
(Lorentz-bandgap), làm cho tường của buồng cộng hưởng có khả năng phản xạ tốt. Tuy nhiên, nó vẫn cho 
phép một lượng hữu hạn photon thoát ra ngoài. 
 Hình 2: Hệ ba lớp, chân không-môi trường-chân không, Tốc độ rã tự phát của ngyên tử ở trạng thái kích thích khi 
 R 0.5 , R 1.5  ; 1.2 
 đặt trên trục đối xứng của khối trụ, với 2T 1 TL T (đường chấm-chấm). 
  0.796  ( 0.7 , 0.38  );R R 5  R 0.5 R 1.5
 L2 TT 2 TP 2 T 1 2 T với 2 T (đường gạch-chấm), 2 T (đường 
 liền nét). 
 Trên hình 2 chúng tôi khảo sát tốc độ rã của nguyên tử khi đặt bên trong khối trụ 3 lớp với giả thiết 
môi trường tạo nên khối trụ là loại vật chất dạng Dru-Lorentz xác định bởi phương trình (5). Ta có thể 
thấy tốc độ rã tự phát của nguyên tử phụ thuộc rất mạnh vào tần số của photon phát xạ cũng như bán kính 
trong cùng và độ dày của lớp vật chất tạo nên khối trụ. Với các tham số vật chất L 1.2  T , bán kính 
trong cùng R2 0.5T và bán kính ngoài R1 1.5T (đường chấm-chấm) ta nhật thấy trong vùng cấm 
tần số T  L tốc độ rã của nguyên tử bị ức chế rất mạnh  / 0 0 , điều đó cho thấy 
nguyên tử có thể được giữ yên ở trạng thái kích thích mà không bị rã. Ngoài vùng tần số này, về hai phía, 
tốc độ rã của nguyên tử dao động mạnh và đạt một cực đại về phía bên phải ở vùng tần số gần với L . 
Trên hình 2 chúng tôi cũng vẽ cho tình huống thay đổi các tham số vật chất của môi trường để khảo sát 
ảnh hưởng của vật chất lên tốc độ rã, lúc này chúng tôi chọn các tham số của môi trường 
 L2 0.796  TT ( 2 0.7  TP , 2 0.38  T ) , và tăng độ dày của khối trụ R1 R 2 5T cố định bán 
kính trong của khối trụ R2 0.5T (đường gạch-chấm). Lúc này, cũng có thể thấy được trong vùng cấm 
tần số P2  L 2 tốc độ rã nguyên tử cũng bị ức chế mạnh và xuất hiện một đỉnh cộng hưởng rất cao 
ở về phía vùng tần số bên trái của vùng cấm. Khi giữ nguyên các tham số vật chất của môi trường, cố 
định độ dày khối trụ (lớp 2) như cũ và tăng bán kính trong của khối trụ R2 1.5T (đường liền nét) tình 
© 2019 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
 TỐC ĐỘ RÃ TỰ PHÁT VÀ ĐỘ DỊCH MỨC NĂNG LƯỢNG CỦA MỘT 109 
 NGUYÊN TỬ HAI MỨC KHI CÓ MẶT KHỐI TRỤ VẬT CHẤT NHIỀU LỚP 
hình cũng diễn ra tương tự trong vùng cấm tần số. Tuy nhiên, đỉnh cộng hưởng lúc này dịch về phía phải 
vùng cấm, phía tần số cao hơn. 
 Hình 3: Hệ bốn lớp, chân không-môi trường-môi trường-chân không, Môi trường ở lớp thứ 2 là giống như ở hình 2, 
  1.2  R R 5 R R 4
 môi trường ở lớp thứ 3 có L T , với 1 2 T (đường liền nét), 1 2 T (đường chấm-chấm) và 
 2
 T (đường gạch-chấm). 
 Trên hình 3 chúng tôi cố định lớp thứ 2 có các tham số vật chất 
 L2 0.796  TT ( 2 0.7  TP , 2 0.38  T ) giống như trong hình 2 và tạo thêm một lớp thứ 3 bên 
trong, với tham số L 1.2  T và lần lượt thay đổi độ dày của lớp thứ 2, R1 R 2 5T (đường liền 
nét), R1 R 2 4T (đường chấm-chấm) và R1 R 2 2T (đường gạch-chấm). Hình vẽ cũng cho thấy 
ảnh hưởng của môi trường vật chất tạo nên tường trong cùng của buồng cộng hưởng lên tốc độ rã của 
ngyên tử. Bên trong vùng cấm tần số, tốc độ rã của nguyên tử tiến về không, hay nói cách khác nguyên tử 
bị giữ nguyên ở trạng thái kích thích mà không rã được. Bên ngoài vùng tần số này, tốc độ rã dao dộng 
mạnh và có những cộng hưởng cả về hai phía tần số cao hơn và thấp hơn tần số trong vùng cấm. Ngoài ra, 
đối với hệ 4 lớp chúng ta cũng có thể thấy được dáng điệu của tốc độ rã có 2 vùng cấm trong khoảng từ 
 / T 1.1  1.2 và / T 0.7  0.8. Có thể thấy vùng thứ nhất là do tường trong cùng (lớp 3) của 
buồng cộng hưởng gây ra và vùng cấm thứ 2 là do lớp bên ngoài (lớp 2). Ở về hai phía tần số cao hơn và 
thấp hơn của hai vùng cấm này chúng ta cũng thấy được các đỉnh cộng hưởng, ở những vị trí này, tốc độ 
rã của nguyên tử tăng mạnh. Ngoài ra cũng có thể thấy được các đường tương ứng với độ dày của lớp vật 
chất bên ngoài (lớp 2) tăng từ 2T 5  T thì dáng điệu của các đường cũng không phân biệt rõ ràng, điều 
này có thể giải thích rằng, độ dày của lớp ngoài, tạo nên một sự giam nhốt trường rất tốt và đạt giá trị bão 
hòa khi độ dày cỡ 2T , ở giá trị này, tăng độ dày lên nữa cũng không làm thay đổi tính chất của hệ. 
 © 2019 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
110 TỐC ĐỘ RÃ TỰ PHÁT VÀ ĐỘ DỊCH MỨC NĂNG LƯỢNG CỦA MỘT 
 NGUYÊN TỬ HAI MỨC KHI CÓ MẶT KHỐI TRỤ VẬT CHẤT NHIỀU LỚP 
 Si/ SiO
Hình 4: Hệ trụ nhiều lớp có dạng gương phản xạ Bragg với 8 cặp lớp 2 . Tốc độ rã tự phát được vẽ như một 
 R 0.1 0.5 
 hàm phụ thuộc tần số với N 1 T (đường chấm-chấm), T (đường gạch-chấm), và T (đường liền nét). 
  0.748 
 Tâm vùng cấm tần số 0 T 
 Trên hình 4 chúng tôi vẽ tốc độ rã tự phát của nguyên tử như một hàm của tần số, bán kính trong 
cùng của khối trụ RN 1 0.1 T (đường chấm-chấm), 0.5T (đường gạch chấm) và T (đường liền nét). 
Dáng điệu đồ thị cũng diễn ra tương tự như các trường hợp trên, trong vùng cấm tần số, tốc độ rã cũng bị 
ức chế mạnh, ở vùng tần số cao hơn cũng xuất hiện đỉnh cộng hưởng. Đỉnh cộng hưởng dịch về phía tần 
số cao hơn khi bán kính trong cùng của khối trụ tăng. 
3.2 Độ dịch mức năng lượng 
 [3d 2 /8] c
Hình 5: Độ dịch mức năng lượng 0 A A phụ thuộc vào bán kính trong cùng của khối trụ nhiều lớp. Cho 
 khối trụ 3 lớp (đường chấm-chấm), 4lớp (đường liền nét) và 8 cặp lớp (đường gạch-chấm). Các tham số khác như 
 trong các hình 2-4. 
© 2019 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
 TỐC ĐỘ RÃ TỰ PHÁT VÀ ĐỘ DỊCH MỨC NĂNG LƯỢNG CỦA MỘT 111 
 NGUYÊN TỬ HAI MỨC KHI CÓ MẶT KHỐI TRỤ VẬT CHẤT NHIỀU LỚP 
 Trên hình 5 chúng tôi vẽ độ dịch mức năng lượng như một hàm của bán kính trong cùng của khối 
trụ. Bán kính trong của khối trụ được chuẩn theo bước sóng T 2 c / T . Với khối trụ ba lớp (đường 
chấm-chấm), bốn lớp (đường liền nét) và 18 lớp Si/SiO2 (đường gạch-chấm). Khi bán kính khối trụ rất 
bé, ta thấy độ dịch mức năng lượng diễn ra rất mạnh. Đối với khối trụ 3 lớp, năng lượng chuyển mức của 
nguyên tử dịch rất mạnh về phía xanh (đường chấm-chấm), trong khi đó đối với khối trụ 4 lớp (đường 
liền nét) và 18 lớp (đường gạch-chấm), năng lượng chuyển mức của nguyên tử dịch về phía đỏ. Tăng dần 
bán kính khối trụ, dáng điệu của tốc độ rã thay đổi rất mạnh và xuất hiện những đỉnh cộng hưởng tại các 
vị trí về hai phía của vùng cấm tần số (xem hình 2). Tại những đỉnh cộng hưởng này, không có sự dịch 
mức năng lượng nguyên tử. Ở vùng tần số cao hơn tần số cộng hưởng, năng lượng chuyển mức nguyên tử 
tăng, ngược lại ở vùng tần số thấp hơn, năng lượng chuyển mức giảm. 
4 KẾT LUẬN 
 Kết quả cho thấy sự giảm mạnh của tốc độ rã tự phát trong vùng cấm của tần số và tại biên của vùng 
này tốc độ rã tăng rất mạnh về phía biên trái của của vùng tần số. Vị trí các đỉnh cộng hưởng phụ thuộc 
vào bán kính trong cùng của khối trụ phân lớp. Tại các vị trí cộng hưởng, độ dịch mức năng lượng bằng 
không. Tại những vị trí không cộng hưởng, năng lượng chuyển mức của nguyên tử dịch về phía xanh ở 
vùng tần số cao hơn tần số cộng hưởng và dịch về phía đỏ ở vùng tần số thấp hơn tần số cộng hưởng. 
Tóm lại, qua những kêt quả tính toán ở trên, đã cho thấy, với hệ trụ có cấu trúc phân lớp, chúng ta có thể 
tạo nên một buồng cộng hưởng có tính chất giam nhốt tốt, có thể giữ được nguyên tử đứng yên ở trạng 
thái kích thích trong một khoảng thời gian như mong muốn. Điều này mang lại triển vọng rất lớn đối với 
việc điều khiển tín hiệu photon trong ống dẫn sóng. 
TÀI LIỆU THAM KHẢO 
[1] Dzsotjan D., Sørensen A.S., and Fleischhauer M. (2010), “Quantum emitters coupled to surface plasmons of a 
 nanowire: A Green’s function approach”, Phys. Rev. B, 82(075427). 
[2] Purcell. E. M. (1946), “Spontaneous emission probabilities at radio frequencies”, Phys. Rev. 69,674. 
[3] Agarwal G.S. (1975), “Quantum electrodynamics in the presence of dielectrics and conductors. IV. General 
 theory for spontaneous emission in finite geomertries”, Phys. Rev. A, 12(1475); Wylie J.M. and Sipe J.E. 
 (1984), “Quantum electrodynamics near an interface”, Phys. Rev. A, 30(1185). 
[4] Ho Trung Dung, Knӧll L., and Welsch D.G. (2000), “Spontaneous decay in the presence of dispersing and 
 absorbing bodies: General theory and application to a spherical cavity”, Phys. Rev. A, 62(053804). 
[5] Rekdal P.K., Scheel S., Knight P.L., and Hinds E.A. (2004), “Thermal spin flips in atom chips”, Phys. Rev. A, 
 70(013811); Fermani R., Scheel S., and Knight P.L. (2007), “Trapping cold atoms near carbon nanotubes: 
 Thermal spin flips and Casimir-Polder potential”, Phys. Rev. A, 75(062905). 
[6] Chen Y.N., Chen G.Y., Chuu D.S., and Brandes T. (2009), “Quantum-dot exciton dynamics with a surface 
 plasmon: Band-edge quantum optics”, Phys. Rev. A, 79(033815). 
[7] Erdogan T., Sullivan K.G., and Hall D.G. (1993), “Enhancement and inhibition of radiation in cylindrically 
 symmetric, periodic structures”, Journal of the Optical Society of America B, 10(391). 
[8] Friedberg R. and Manassah J.T. (2011), “Initial cooperative decay rate and cooperative Lamb shift of resonant 
 atoms in an infinite cylindrical geometry”, Phys. Rev. A, 84(023839). 
[9] Fussell D.P., McPhedran R.C., and Martijn de Sterke C. (2005), “Decay rate and level shift in a circular 
 dielectric waveguide”, Phys. Rev. A, 71(013815). 
[10] Klimov V.V. and Ducloy M. (2004), “Spontaneous emission rate of an excited atom placed near a nanofiber”, 
 Phys. Rev. A, 69(013812). 
[11] Nha H. and Jhe W. (1997), “Cavity quantum electrodynamics for a cylinder: Inside a hollow dielectric and near 
 a solid dielectric cylinder”, Phys. Rev. A, 56(2213). 
 © 2019 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
112 TỐC ĐỘ RÃ TỰ PHÁT VÀ ĐỘ DỊCH MỨC NĂNG LƯỢNG CỦA MỘT 
 NGUYÊN TỬ HAI MỨC KHI CÓ MẶT KHỐI TRỤ VẬT CHẤT NHIỀU LỚP 
[12] Żakowicz W. and Janowicz M. (2000), “Spontaneous emission in the presence of a dielectric cylinder”, Phys. 
 Rev. A, 62(013820). 
[13] Tatur K., Woods L.M., and Bondarev I.V. (2008), “Zero-point energy of a cylindrical layer of finite thickness”, 
 Phys. Rev. A, 78(012110). 
[14] Afanasiev A. and Minogin V. (2010), “van der Waals interaction of an atom with the internal surface of a 
 hollow submicrometer-size cylinder”, Phys. Rev. A, 82(052903). 
[15] Eberlein C. and Zietal R. (2009), “Retarded Casimir-Polder force on an atom near reflecting microstructures”, 
 Phys. Rev. A, 80(012504). 
[16] Ellingsen S.A., Buhmann S.Y., and Scheel S. (2010), “Casimir-Polder potential and transition rate in resonating 
 cylindrical cavities”, Phys. Rev. A, 82(032516). 
[17] Marocico C.A. and Knoester J. (2009), “Intermolecular resonance energy transfer in the presence of a dielectric 
 cylinder”, Phys. Rev. A, 79(053816). 
[18] H. T. Dung and T. M. Hien, "Atomic spontaneous decay near a finite-length dielectric cylinder", Opt. Comm., 
 355, 27-32 (2015). 
[19] A. Einstein, "The Quantum Theory of Radiation", Z. Phys. 18, 121 (1917). 
[20] G. S. Agarwal, "Quantum electrodynamics in the presence of dielectrics and conductors. I. Electromagnetic-
 field response functions and black- body fluctuations in finite geometries", Phys. Rev. A 11, 230 (1975), 
 "Quantum electrodynamics in the presence of dielectrics and conductors. II. Theory of dispersion forces", 
 Phys. Rev. A 11, 243 (1975), "Quantum electrodynamics in the presence of dielectrics and conductors. III. 
 Relations among one-photon transition probabilities in stationary and nonstationary fields, density of states, 
 the field-correlation functions, and surface-dependent response functions", Phys. Rev. A 11, 253 (1975). 
[21] S. M. Barnett, B. Huttner, R. Loudon, and R. Matloob, "Decay of excited atoms in absorbing dielectrics", J. 
 Phys. B: At. Mol. Opt. Phys. 29, 3763 (1996). 
[22] S. M. Barnett, B. Huttner, and R. Loudon, "Spontaneous emission in absorbing dielectric media", Phys. Rev. 
 Lett. 68, 3698 (1992). 
[23] M. Fichet, F. Schuller, D. Bloch, and M. Ducloy, "van der Waals inter-actions between excited-state atoms and 
 dispersive dielectric surfaces", Phys. Rev. A 51, 1553 (1995). 
[24] M. Fleischhauer and S. Yelin, "Radiative atom-atom interactions in optically dense media: Quantum 
 corrections to the Lorentz-Lorenz formula", Phys. Rev. A 59, 2427 (1999). 
[25] M. Fleischhauer, "Spontaneous emission and level shifts in absorbing dis- ordered dielectrics and dense atomic 
 gases: A Green’s-function approach", Phys. Rev. A 60, 2534 (1999). 
[26] Ho Trung Dung, L. Kn¨oll, and D. -G. Welsch, "Spontaneous decay in the presence of dispersing and absorbing 
 bodies: General theory and applica- tion to a spherical cavity", Phys. Rev. A 62, 053804 (2000). 
[27] G. Juzeliunas, "Spontaneous Emission in Absorbing Dielectrics: A Microscopic Approach", Phys. Rev. A 55, 
 R4015 (1997). 
[28] K. Koshino and A. Shimizu, "Spontaneous emission in an absorptive and inhomogeneous cavity", Phys. Rev. A 
 53, 4468 (1996). 
[29] D. Meschede, W. Jhe, and E. A. Hinds, "Radiative properties of atoms near a conducting plane: An old problem 
 in a new light", Phys. Rev. A 41, 1587 (1990). 
[30] S. Scheel, L. Kn¨oll, D. -G. Welsch, and S. M. Barnett, "Quantum local-field corrections and spontaneous 
 decay", Phys. Rev. A 60, 1590 (1999). 
[31] M. S. Tomaˇs and Z. Lenac, "Decay of excited molecules in absorbing planar cavities", Phys. Rev. A 56, 4197 
 (1997). 
[32] J. M.Wylie and J. E. Sipe, "Quantum electrodynamics near an interface", Phys. Rev. A 30, 1185 (1984). 
© 2019 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh 
 TỐC ĐỘ RÃ TỰ PHÁT VÀ ĐỘ DỊCH MỨC NĂNG LƯỢNG CỦA MỘT 113 
 NGUYÊN TỬ HAI MỨC KHI CÓ MẶT KHỐI TRỤ VẬT CHẤT NHIỀU LỚP 
[33] M. S. Yeung and T. K. Gustafson, "Spontaneous emission near an absorbing dielectric surface", Phys. Rev. A 
 54, 5227 (1996). 
[34] S. Y. Buhmann and D.-G.Welsch, "Born expansion of the Casimir–Polder interaction of a ground-state atom 
 with dielectric bodies", Appl. Phys. B: Lasers Opt. 82, 189 (2006). 
[35] L.-W. Li, M.-S. Leong, T.-S. Yeo, and P.-S. Kooi (2000), “Electromagnetic dyadic Green’s functions in 
 spectral domain for multilayered cylinders”, Journal of Electromagnetic Waves and Applications, Vol. 14, 
 961-985, pp.961-972. 
 Ngày nhận bài: 01/04/2019 
 Ngày chấp nhận đăng: 30/07/2019 
 © 2019 Trường Đại học Công nghiệp Thành phố Hồ Chí Minh