Tổ chức cho học sinh Lớp 12 tiếp cận bài toán phỏng thực tiễn về ứng dụng tích phân để tính thể tích các khối tròn xoay

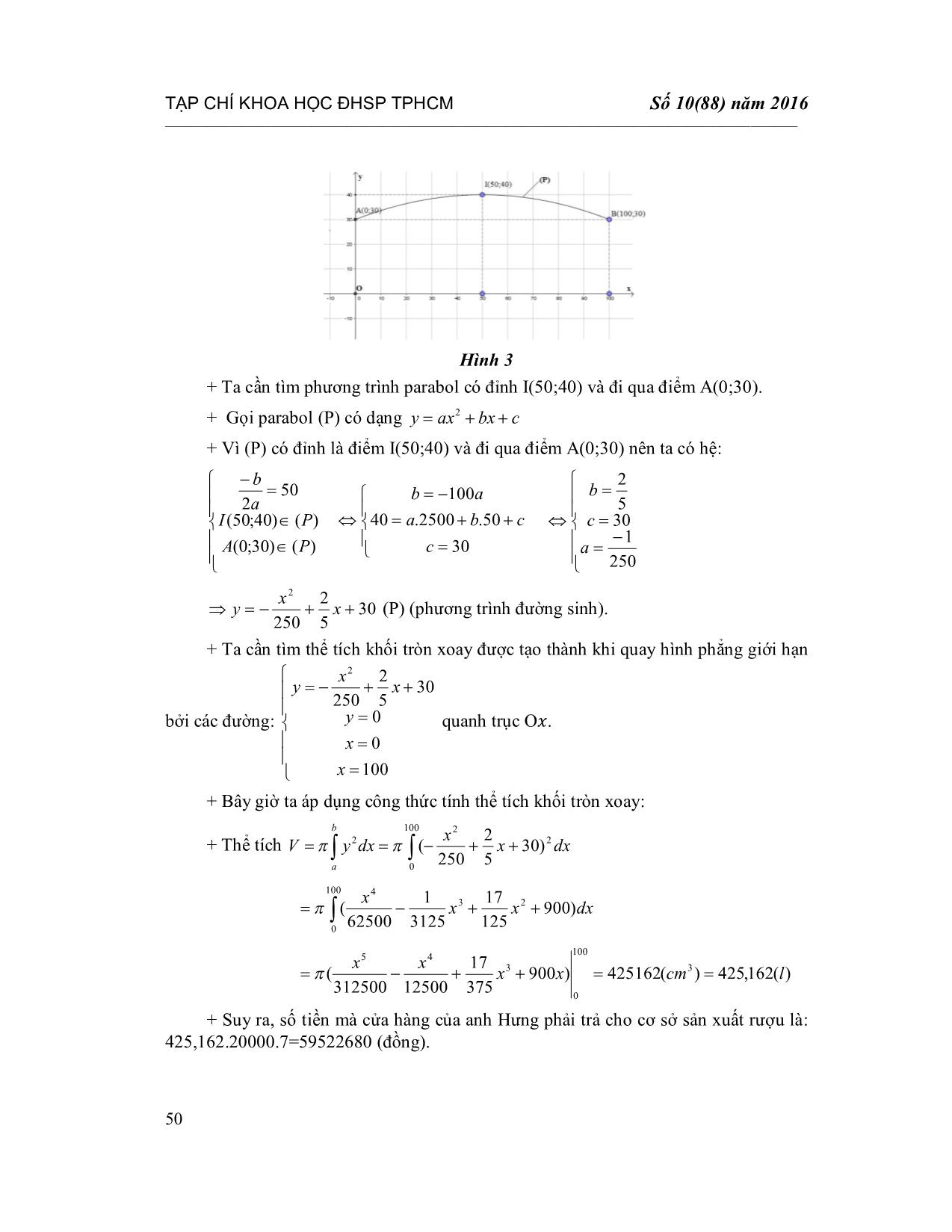
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 10(88) năm 2016 
____________________________________________________________________________________________________________ 
44 
TỔ CHỨC CHO HỌC SINH LỚP 12 TIẾP CẬN BÀI TOÁN 
 PHỎNG THỰC TIỄN VỀ ỨNG DỤNG TÍCH PHÂN 
ĐỂ TÍNH THỂ TÍCH CÁC KHỐI TRÒN XOAY 
DƯƠNG HỮU TÒNG*, TRẦN TRÍ TÂM** 
TÓM TẮT 
Trong chương trình toán 12, có hai cách tiếp cận bài toán tính thể tích V các khối 
tròn xoay: Dựa vào công thức trong hình học, dựa vào công thức trong giải tích. Sách giáo 
khoa Giải tích 12 hiện hành giới thiệu cho học sinh tiếp cận bài toán tính thể tích các khối 
tròn xoay dựa trên công cụ tích phân. Tuy nhiên, hoạt động giải toán chỉ gắn liền với tính 
thể tích các khối tròn xoay khi quay hình phẳng giới hạn bởi các đường cong cho trước 
phương trình mà không thông qua giải một bài toán thực tiễn về ứng dụng tích phân để 
tính thể tích các khối tròn xoay. Để khắc phục được hạn chế này, bài báo tổ chức cho học 
sinh lớp 12 tiếp cận bài toán phỏng thực tiễn về ứng dụng tích phân để tính thể tích của 
thùng rượu và tính khối lượng quả dưa hấu. 
Từ khóa: tính thể tích khối tròn xoay, ứng dụng của tích phân, bài toán phỏng thực 
tiễn. 
ABSTRACT 
Helping students in class 12 to approach imitatively real problems 
of applying integrals in calculating the volume of the block of revolution 
In mathematical curriculum 12, there are two approaches to the volume V of the 
block of revolution: based on the formula V in geometry and based on the formula V in the 
calculus. The current calculus textbook 12 introduces students to the volume V of the block 
of revolution based on the integral tools. However, activities of solving problems are only 
associated with the volume V of the block of revolution when plane figures are turned and 
limited by curves with the given equations, so they are not related to real problems of 
applications of integrals to calculate the volume of the block of revolution. To overcome 
this limitation, the paper helps students in class 12 to approach imitatively real problems 
of applying integrals in calculating the volume of a barrel of wine and a watermelon. 
Keywords: calculate the volume of the block of revolution, applications of integrals, 
imitatively real problems. 
1. Đặt vấn đề 
Trong toán học, một khái niệm hay một công thức thường xuất hiện gắn liền với 
hoạt động giải toán và ứng dụng của các hoạt động ấy. Thế nhưng, sách giáo khoa 
(SGK) Giải tích 12 không đề xuất các kiểu nhiệm vụ gắn liền với bài toán phỏng thực 
* TS, Trường Đại học Cần Thơ; Email: dhtong@ctu.edu.vn 
** HVCH, Trường Đại học Cần Thơ 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Hữu Tòng và tgk 
_____________________________________________________________________________________________________________ 
45 
tiễn về ứng dụng tích phân để tính thể tích các khối tròn xoay, trong đó bài toán phỏng 
thực tiễn là bài toán mà các dữ kiện, các biến, các yêu cầu, các câu hỏi, các mối quan 
hệ không phải là các yếu tố của thực tiễn “thực” mà chỉ là sự mô phỏng của thực 
tiễn này. Điều này làm cho học sinh (HS) chưa thấy đầy đủ được ứng dụng của tích 
phân để tính thể tích các khối tròn xoay có trong thực tiễn. Mục đích chính của bài báo 
là xây dựng tình huống đưa vào bài toán phỏng thực tiễn về ứng dụng của tích phân để 
tính thể tích các khối tròn xoay cho HS lớp 12 giải quyết. 
2. Khung lí thuyết tham chiếu 
Để xây dựng tình huống dạy học, chúng tôi sử dụng một số khái niệm quan trọng 
trong lí thuyết tình huống do G.Brousseau đặt nền móng. 
2.1. Biến didactic 
Một họ các bài toán có thể được sinh ra từ một tình huống bằng việc thay đổi 
những giá trị của một số biến. Các biến này, đến lượt nó, lại làm thay đổi những đặc 
trưng của các chiến lược giải (độ khó khăn, tính hợp thức, sự phức tạp). Chúng sẽ là 
biến didactic nếu bằng cách tác động lên chúng, người ta có thể tạo nên những thích 
nghi và những điều tiết của việc học tập. 
G.Brousseau gọi biến didactic là những biến có thể làm thay đổi đặc trưng của 
những chiến lược giải hay câu trả lời của HS và giáo viên (GV) có thể thực hiện việc 
lựa chọn các giá trị của biến (tham khảo Bessot A. và các tác giả, năm, tr. 145). 
2.2. Chiến lược cơ sở và chiến lược tối ưu 
Đứng trước một vấn đề được đặt ra trong tình huống dạy học, HS có thể có một 
chiến lược tìm câu trả lời. Nhưng câu trả lời ban đầu này có thể không phải là cái mà 
GV muốn giảng dạy. Khi đó, chiến lược tìm câu trả lời được gọi là “chiến lược cơ sở”. 
Hiển nhiên, chiến lược cơ sở liên quan đến những kiến thức cũ, cho phép HS có một 
hiểu biết ban đầu về bài toán đặt ra. 
Chiến lược cơ sở phải nhanh chóng tỏ ra khiếm khuyết hoặc không hiệu quả. 
Điều này buộc HS phải tiến hành những điều tiết, những sửa đổi trong hệ thống kiến 
thức của mình. HS đều phải lưỡng lự khi chọn các quyết định. Mong muốn của GV là 
HS chuyển từ chiến lược cơ sở đến chiến lược tối ưu. Thông thường, chiến lược tối ưu 
này chứa đựng kiến thức mới ... n xoay khi quay hình phẳng giới hạn 
bởi elip xung quanh trục Oy, suy ra kết quả. 
d. Ảnh hưởng các giá trị của biến được chọn đến các chiến lược 
Bảng 1. Giá trị của biến được lựa chọn trong bài toán 1 và bài toán 2 
Bài toán V1 V2 
Bài toán 1 
(Thùng rượu) 
Có tâm đối xứng Đường sinh có trục đối xứng 
Bài toán 2 
(Quả dưa hấu) 
Có tâm đối xứng Đường sinh có trục đối xứng 
Giá trị “có tâm đối xứng” của biến V1 trong cả 2 bài toán tạo điều kiện thuận lợi 
cho HS tiến hành chọn hệ trục tọa độ Oxy, lập phương trình và tính thể tích các khối 
tròn xoay vì chọn giá trị này bài toán sẽ rơi vào các trường hợp đặc biệt, người giải sẽ 
dễ dàng giải quyết bài toán. Do đó, giá trị này đem đến thuận lợi cho chiến lược S12, 
S13, S22, S23. 
Biến V2 nhận giá trị “đường sinh có trục đối xứng ” đem đến thuận lợi cho các 
chiến lược S12, S13. Ngoài ra, nó còn gây rất nhiều khó khăn cho HS như: phải đổi 
biến từ x sang biến y, không quen quan sát hình ảnh cũng như làm việc với đối tượng là 
biến y. Do đó chiến lược S2 bị hạn chế phần nào và góp phần tạo cơ hội cho nhóm 
chiến lược S1 xuất hiện. 
e. Những quan sát có thể 
Những lời giải có thể đối với bài toán 1: (Tính thể tích thùng rượu) 
- Ứng với các biến đã chọn, ta có chiến lược S11 và hướng giải bài toán 1 có thể 
quan sát được như sau: 
+ Ta sẽ để thùng rượu nằm ngang để thuận lợi trong việc tính toán. Chọn hệ trục 
tọa độ Oxy sao cho O trùng tâm mặt đáy của thùng rượu, từ đề bài ta có hình vẽ sau. 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 10(88) năm 2016 
____________________________________________________________________________________________________________ 
50 
Hình 3 
+ Ta cần tìm phương trình parabol có đỉnh I(50;40) và đi qua điểm A(0;30). 
+ Gọi parabol (P) có dạng cbxaxy 2 
+ Vì (P) có đỉnh là điểm I(50;40) và đi qua điểm A(0;30) nên ta có hệ: 
)()30;0(
)()40;50(
50
2
PA
PI
a
b
30
50.2500.40
100
c
cba
ab
250
1
30
5
2
a
c
b
30
5
2
250
2
 xxy
(P) (phương trình đường sinh). 
+ Ta cần tìm thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn 
bởi các đường: 
100
0
0
30
5
2
250
2
x
x
y
xxy
 quanh trục Oݔ. 
+ Bây giờ ta áp dụng công thức tính thể tích khối tròn xoay: 
+ Thể tích dxxxdxyV
b
a
2
100
0
2
2 )30
5
2
250
( 
 dxxxx )900
125
17
3125
1
62500
( 23
100
0
4
 )(162,425)(425162)900
375
17
12500312500
( 3
100
0
3
45
lcmxxxx 
+ Suy ra, số tiền mà cửa hàng của anh Hưng phải trả cho cơ sở sản xuất rượu là: 
425,162.20000.7=59522680 (đồng). 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Hữu Tòng và tgk 
_____________________________________________________________________________________________________________ 
51 
- Ứng với các biến đã chọn, ta có chiến lược S12 và hướng giải bài toán 1 có thể 
quan sát được như sau: 
+ Ta sẽ để thùng rượu nằm ngang để thuận lợi trong việc tính toán. Chọn hệ trục 
tọa độ Oxy sao cho O trùng với tâm đối xứng của thùng rượu từ đề bài ta vẽ hình và 
chọn tọa độ đỉnh I, điểm B. 
+ Ta cần tìm phương trình parabol có đỉnh I(0;40) và qua điểm B(50;30) 
+ Gọi parabol (P) có dạng cbxaxy 2 
+ Vì (P) có đỉnh là điểm I(0;40) và đi qua điểm B(50;30) nên ta có hệ: 
)()30;50(
)()40;0(
0
2
PB
PI
a
b
4050.2500.30
40
0
2
ba
c
a
b
250
1
40
0
a
c
b
40
250
2
xy (P) (phương trình cạnh thùng rượu). 
+ Ta cần tìm thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn 
bởi các đường: 
50
50
0
40
250
2
x
x
y
xy
 quanh trục Oݔ. 
+ Bây giờ ta áp dụng công thức tính thể tích khối tròn xoay: 
+ Thể tích dxxdxyV
b
a
2
50
50
2
2 )40
250
( 
dxxx )1600
250
80
62500
( 2
50
50
4
)(162,425)(425162)1600
750
80
312500
( 3
50
50
3
5
lcmxxx 
+ Suy ra, số tiền mà cửa hàng của anh Hưng phải trả cho cơ sở sản xuất rượu là: 
425,162.20000.7=59522680 (đồng). 
- Ứng với các biến đã chọn, ta có chiến lược S21 và hướng giải bài toán 1 có thể 
quan sát được như sau: 
+ Ta sẽ để thùng rượu đứng. Chọn hệ trục tọa độ Oxy sao cho O trùng tâm mặt 
đáy của thùng rượu, từ đề bài ta vẽ hình và chọn tọa độ đỉnh I, điểm A. 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 10(88) năm 2016 
____________________________________________________________________________________________________________ 
52 
+ Ta cần tìm phương trình parabol có đỉnh I(40;50) và đi qua điểm A(30;0). 
+ Gọi parabol (P) có dạng cbyayx 2 
+ Vì (P) có đỉnh là điểm I(40;50) và đi qua điểm A(30; 0) nên ta có hệ: 
)()0;30(
)()50;40(
50
2
PA
PI
a
b
30
50.2500.40
100
c
cba
ab
250
1
30
5
2
a
c
b
30
5
2
250
2
 yyx
(P) (phương trình đường sinh). 
+ Ta cần tìm thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn 
bởi các đường: 
100
0
0
30
5
2
250
2
y
y
x
yyx
 quanh trục Oy. 
+ Bây giờ ta áp dụng công thức tính thể tích khối tròn xoay: 
+ Thể tích dyyydyxV
b
a
2
100
0
2
2 )30
5
2
250
( 
 dyyyy )900
125
17
3125
1
62500
( 23
100
0
4
 )(162,425)(425162)900
375
17
12500312500
( 3
100
0
3
45
lcmyyyy 
+ Suy ra, số tiền mà cửa hàng của anh Hưng phải trả cho cơ sở sản xuất rượu là: 
425,162.20000.7=59522680 (đồng). 
- Ứng với các biến đã chọn, ta có chiến lược S22 và hướng giải bài toán 1 có thể 
quan sát được như sau: 
+ Ta sẽ để thùng rượu đứng. Chọn hệ trục tọa độ Oxy sao cho O trùng với tâm 
đối xứng của thùng rượu từ đề bài, ta vẽ hình và chọn tọa độ đỉnh I, điểm A, B. 
+ Ta cần tìm phương trình parabola có đỉnh I(0;40) và qua điểm A(30;50) 
+ Gọi parabol (P) có dạng cbyayx 2 
+ Vì (P) có đỉnh là điểm I(0;40) và đi qua điểm A(30;50) nên ta có hệ: 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Hữu Tòng và tgk 
_____________________________________________________________________________________________________________ 
53 
)()50;30(
)()0;40(
0
2
PA
PI
a
b
4050.2500.30
40
0
2
ba
c
a
b
250
1
40
0
a
c
b
40
250
2
yx
(P) (phương trình đường sinh). 
+ Ta cần tìm thể tích khối tròn xoay được tạo thành khi quay hình phẳng giới hạn 
bởi các đường: 
50
50
0
40
250
2
y
y
x
yx
 quanh trục Oy. 
+ Bây giờ ta áp dụng công thức tính thể tích khối tròn xoay: 
+ Thể tích dyydxxV
b
a
2
50
50
2
2 )40
250
( 
dyyy )1600
250
80
62500
( 2
50
50
4
)(162,425)(425162)1600
750
80
312500
( 3
50
50
3
5
lcmyyy 
+ Suy ra, số tiền mà cửa hàng của anh Hưng phải trả cho cơ sở sản xuất rượu là: 
425,162.20000.7=59522680 (đồng). 
Những lời giải có thể đối với bài toán 2: (Tính khối lượng quả dưa hấu) 
- Ứng với các biến đã chọn, ta có chiến lược S13 và hướng giải bài toán 2 có thể 
quan sát được như sau: 
+ Ta sẽ để quả dưa nằm ngang để thuận lợi trong việc tính toán. Chọn hệ trục tọa 
độ Oxy sao cho O trùng tâm quả dưa hấu và trục lớn của elip nằm trên trục Ox bằng 28, 
trục nhỏ nằm trên trục Oy bằng 25. 
Hình 4. 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 10(88) năm 2016 
____________________________________________________________________________________________________________ 
54 
+ Ta biết quả dưa hấu có dạng elip tròn xoay, ta cần tìm phương trình elip trong 
tọa độ 2 chiều có độ dài trục lớn là 28, độ dài trục nhỏ là 25. 
+ Ta dùng công thức: )(,12
2
2
2
ba
b
y
a
x
+ Với ܽ là nửa trục lớn và ܾ là nửa trục nhỏ. 
+ Với công thức tính thể tích, ta cần biểu diễn công thức theo y2 và điều này rất 
dễ để thực hiện: 2222222
2
2
2
1 baaybx
b
y
a
x
)( 222
2
2 xa
a
by 
+ Vì 14 a và 5,12 b ta được: 
)196(797,0)14(
14
25,1 222
2
2
2 xxy 
+ Có phương trình elip, ta áp dụng tích phân để tính thể tích 
14
0
14
0
22 )196(797,022 dxxdxyV 
14
0
2 )196(797,0.2 dxx 
33
14
0
3
161,99161)
3
196(504,2.2 dmcmxx 
Vậy khối lượng quả dưa hấu là kg7,895,0.161,9 
- Ứng với các biến đã chọn, ta có chiến lược S23 và hướng giải bài toán 2 có thể 
quan sát được như sau: 
+ Ta sẽ để quả dưa đứng. Chọn hệ trục tọa độ Oxy sao cho O trùng tâm quả dưa 
hấu và trục lớn của elip nằm trên trục Oy bằng 28, trục nhỏ nằm trên trục Ox bằng 25. 
+ Ta biết quả dưa hấu có dạng elip tròn xoay, ta cần tìm phương trình elip trong 
tọa độ 2 chiều có độ dài trục lớn là 28, độ dài trục nhỏ là 25. 
+ Ta dùng công thức: )(,12
2
2
2
ba
b
y
a
x
+ Với b là nửa trục lớn và a là nửa trục nhỏ. 
+ Với công thức tính thể tích, ta cần biểu diễn công thức theo 2x và điều này rất 
dễ để thực hiện: 2222222
2
2
2
1 baaybx
b
y
a
x
)( 222
2
2 yb
b
ax 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Hữu Tòng và tgk 
_____________________________________________________________________________________________________________ 
55 
+ Vì 5,12 a và 14 b , ta được: 
)196(797,0)14(
14
25,1 222
2
2
2 yyx 
+ Có phương trình elip, ta áp dụng tích phân để tính thể tích 
14
0
14
0
22 )196(797,022 dyydyxV 
14
0
2 )196(797,0.2 dyy 
33
14
0
3
161,99161)
3
196(504,2.2 dmcmyy 
Vậy khối lượng quả dưa hấu là kg7,895,0.161,9 
4. Kết quả và thảo luận 
Thực nghiệm được chúng tôi triển khai tại lớp 12TN (35 HS) Trường THPT Tây 
Đô, huyện Long Mỹ, tỉnh Hậu Giang, thời gian: vào tiết 3, tiết 4 buổi sáng thứ 5, ngày 
17 tháng 3 năm 2016. Các số liệu được chúng tôi thu thập bao gồm kết quả thảo luận 
của 5 nhóm, kết quả phiếu làm bài cá nhân của 35 HS. 
4.1. Pha 1. Ôn tập lại kiến thức cũ 
a. Cách xác định phương trình parabol, elip 
b. Công thức thể tích khối tròn xoay khi quay hình phẳng xung quanh 
i). Trục Ox là: 
b
a
dxyV 2 ii).Trục Oy là: 
b
a
dyxV 2 
4.2. Pha 2. 
Bảng 2. Bảng thống kê chiến lược giải của các nhóm đối với bài toán 1 
 Chiến lược S11 Chiến lược S12 Chiến lược S21 Chiến lược S22 
Bài toán 1 0 (0%) 4 (80%) 0 (0%) 1 (20%) 
Đây là lần đầu tiên các nhóm tiếp cận việc giải bài toán phỏng thực tiễn, do đó 
các em có nhiều lúng túng trong việc xác định hướng giải. Họ được sự can thiệp của 
GV cộng với kiến thức lập phương trình đã được nhắc lại ở pha 1 nên các nhóm hầu hết 
sử dụng chiến lược S12 để tìm lời giải cho bài toán. Ngoài ra, đa phần HS chọn chiến 
lược này cũng có thể do các em quen với cách lập phương trình parabol có trục đối 
xứng là trục Oy nên chiến lược S12 dễ dàng xuất hiện. Sau đây là bài làm của một 
nhóm. 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 10(88) năm 2016 
____________________________________________________________________________________________________________ 
56 
Ngoài ra, nhóm 3 chọn chiến lược S22, chiến lược của nhóm này có phần khác 
với 4 nhóm trước đó là chọn cách lập parabol có trục đối xứng là trục Ox, với cách 
chọn này HS phải làm việc với đối tượng là biến y và phải quay hình phẳng quanh trục 
Oy. 
Qua pha 2, chúng tôi nhận thấy các nhóm đã chuyển từ bài toán phỏng thực tiễn 
thành bài toán toán học rất dễ dàng. Trong đó, tất cả các nhóm đã lập được bài toán 
toán học mặc dù có 1 nhóm khác với 4 nhóm còn lại nhưng kết quả vẫn tốt và đúng 
như những gì mong đợi của chúng tôi. Tóm lại, tất cả các nhóm làm tốt pha 2 này. 
4.3. Pha 3 
Nhiệm vụ các nhóm là giải bài toán toán học và trả về kết quả thực tiễn, các chiến 
lược giải được tiếp nối từ pha 2. Ở đây, các nhóm phải giải tiếp những bài toán toán 
học mà các nhóm vừa lập, đặc biệt ở pha này các nhóm tự giải quyết bài toán không có 
sự can thiệp của GV. Kết quả cho thấy các nhóm làm rất tốt 4/5 nhóm tính thể tích khối 
tròn xoay khi quay hình phẳng xung quanh trục Ox và trả về kết quả thực tiễn như 
mong đợi của chúng tôi. Kết quả tiêu biểu của một trong bốn nhóm như sau: 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Hữu Tòng và tgk 
_____________________________________________________________________________________________________________ 
57 
Bên cạnh đó, nhóm còn lại tính thể tích khối tròn xoay khi quay hình phẳng xung 
quanh trục Oy và trả về kết quả thực tiễn đúng đáp án bài toán 1. 
4.4. Pha 4 
Các nhóm cùng sửa bài toán 1 với GV, điều này cũng tương tự như pha hoạt động 
nhóm, hoạt động sửa bài tập diễn ra rất thuận lợi. Các nhóm lần lượt trình bày kết quả 
bài giải của nhóm mình, các nhóm khác nhận xét, góp ý; hầu như 100% các nhóm làm 
đúng bài tập 1, tiến trình thảo luận diễn ra rất nhanh đúng như thời gian dự kiến của 
chúng tôi. Qua pha 4, chúng tôi có thể khẳng định rằng đã đạt được mục tiêu đề ra là 
giới thiệu cho HS rằng có thể dùng tích phân để giải quyết bài toán phỏng thực tiễn. 
4.5. Pha 5 
Cuối tiết dạy, chúng tôi phát phiếu điều tra (chứa nội dung bài toán 2) cho HS 
nhằm kiểm tra sự hiểu biết của các em về việc ứng dụng tích phân để tính khối lượng 
của quả dưa hấu. Sau đây là kết quả thu được từ các phiếu làm bài của cá nhân HS. 
Bảng 3. Bảng thống kê câu trả lời của HS đối với bài toán 2 
Câu trả lời 
của HS 
Giải được 
bài toán 2 
Hiểu vấn đề nhưng giải 
chưa đến kết quả 
Không giải được 
bài toán 2 
Tỉ lệ 32/35 (91,4%) 3/35 (8,6%) 0/35 (0%) 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Số 10(88) năm 2016 
____________________________________________________________________________________________________________ 
58 
Trong Bảng 3 trên, có 32 phiếu đã hoàn thành tốt và đúng đáp án, đa số các em sử 
dụng chiến lược S13 để giải, chỉ một vài em sử dụng chiến lược S23. Bên cạnh đó, có 
3/35 HS (chiếm 8,6%) chưa ra kết quả cuối cùng và kết quả của một HS như sau: 
Qua bài giải cho thấy HS đã biết chuyển từ việc tính khối lượng quả dưa hấu đưa 
về việc tính thể tích khối tròn xoay (tức là HS đã chuyển được bài toán phỏng thực tiễn 
về bài toán toán học) nhưng tới khi HS giải bài toán toán học HS lại giải sai, trong đó 
nguyên nhân là em này đã rút 2y theo biến x chưa đúng (tức lỗi kĩ thuật tính toán chứ 
không phải kĩ thuật quy trình), dẫn đến lấy nguyên hàm sai và HS này chưa ra kết quả 
của bài toán. 
5. Kết luận 
Qua thực nghiệm, chúng tôi nhận thấy số đông các em thành công với việc ứng 
dụng tích phân để tính thể tích của thùng rượu và quả dưa hấu. Hơn nữa, hầu hết HS 
của lớp thực nghiệm đều biết được cách giải quyết bài toán phỏng thực tiễn và đã vận 
dụng khá hiệu quả trong pha 5. Tuy vậy, có một HS chưa đưa ra kết quả chính xác do 
biến đổi phương trình sai, dẫn đến tìm nguyên hàm của hàm số không đúng. Nhưng em 
này cũng hiểu được sự cần thiết phải chuyển bài toán phỏng thực tiễn đã cho về bài 
toán ứng dụng tích phân để tính thể tích khối tròn xoay. 
TẠP CHÍ KHOA HỌC ĐHSP TPHCM Dương Hữu Tòng và tgk 
_____________________________________________________________________________________________________________ 
59 
TÀI LIỆU THAM KHẢO 
1. Annie Bessot, Claude Comiti, Lê Thị Hoài Châu, Lê Văn Tiến (2009), Những yếu tố 
cơ bản của Didactic Toán, Nxb Đại học Quốc gia TP Hồ Chí Minh. 
2. Trần Văn Hạo (Tổng chủ biên) (2008), Giải tích 12, Nxb Giáo dục. 
3. Trần Văn Hạo (Tổng chủ biên) (2008), Giải tích 12 – Sách Giáo viên, Nxb Giáo dục. 
4. Lê Văn Tiến (2005), Phương pháp dạy học môn toán ở trường phổ thông, Nxb Đại 
học Quốc gia TP Hồ Chí Minh. 
5. Vũ Tuấn (Chủ biên) (2008), Bài tập Giải tích 12, Nxb Giáo dục. 
(Ngày Tòa soạn nhận được bài: 02-6-2016; ngày phản biện đánh giá: 15-7-2016; 
ngày chấp nhận đăng: 21-10-2016)