Theoretical and experimental analysis of the exact receptance function of a clamped - Clamped beam with concentrated masses

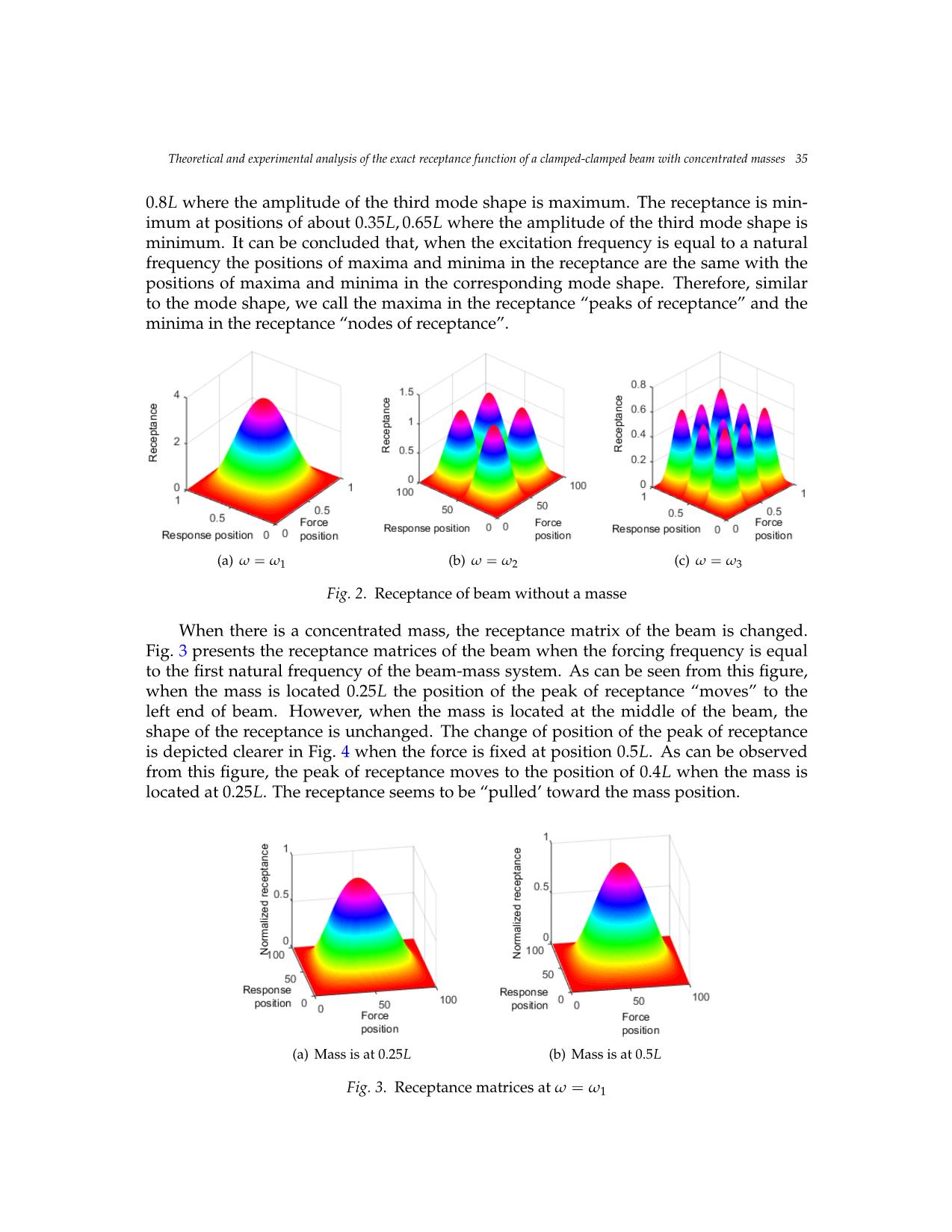
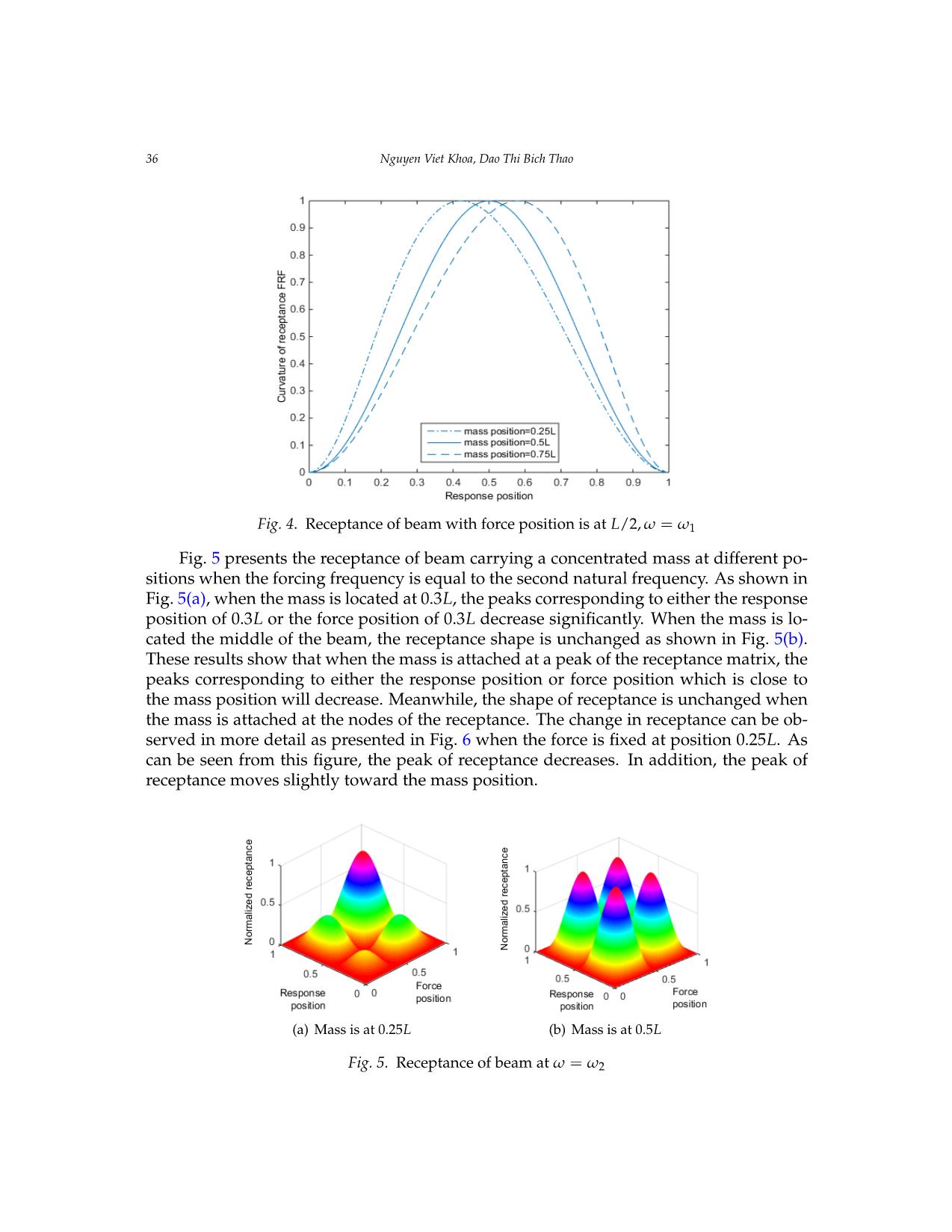
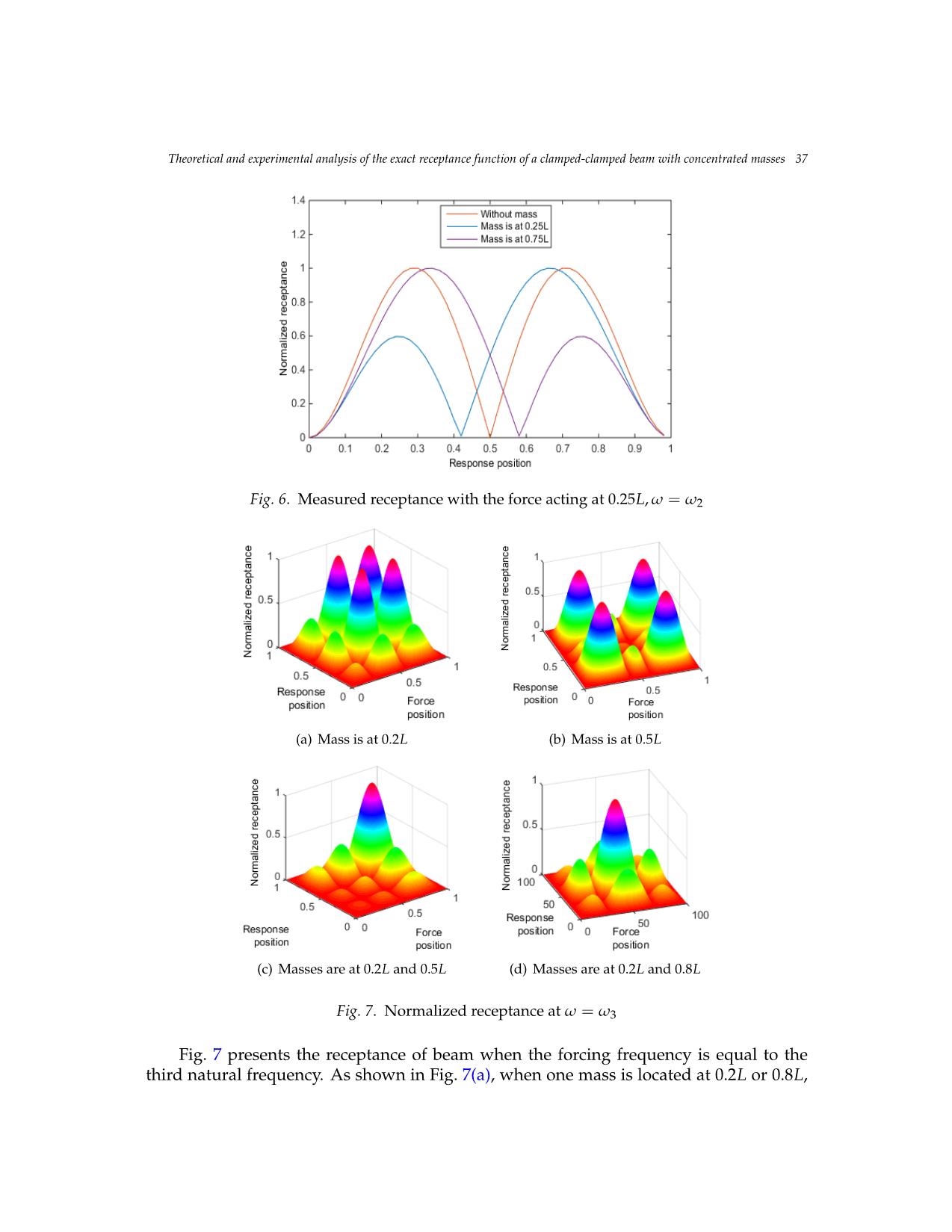
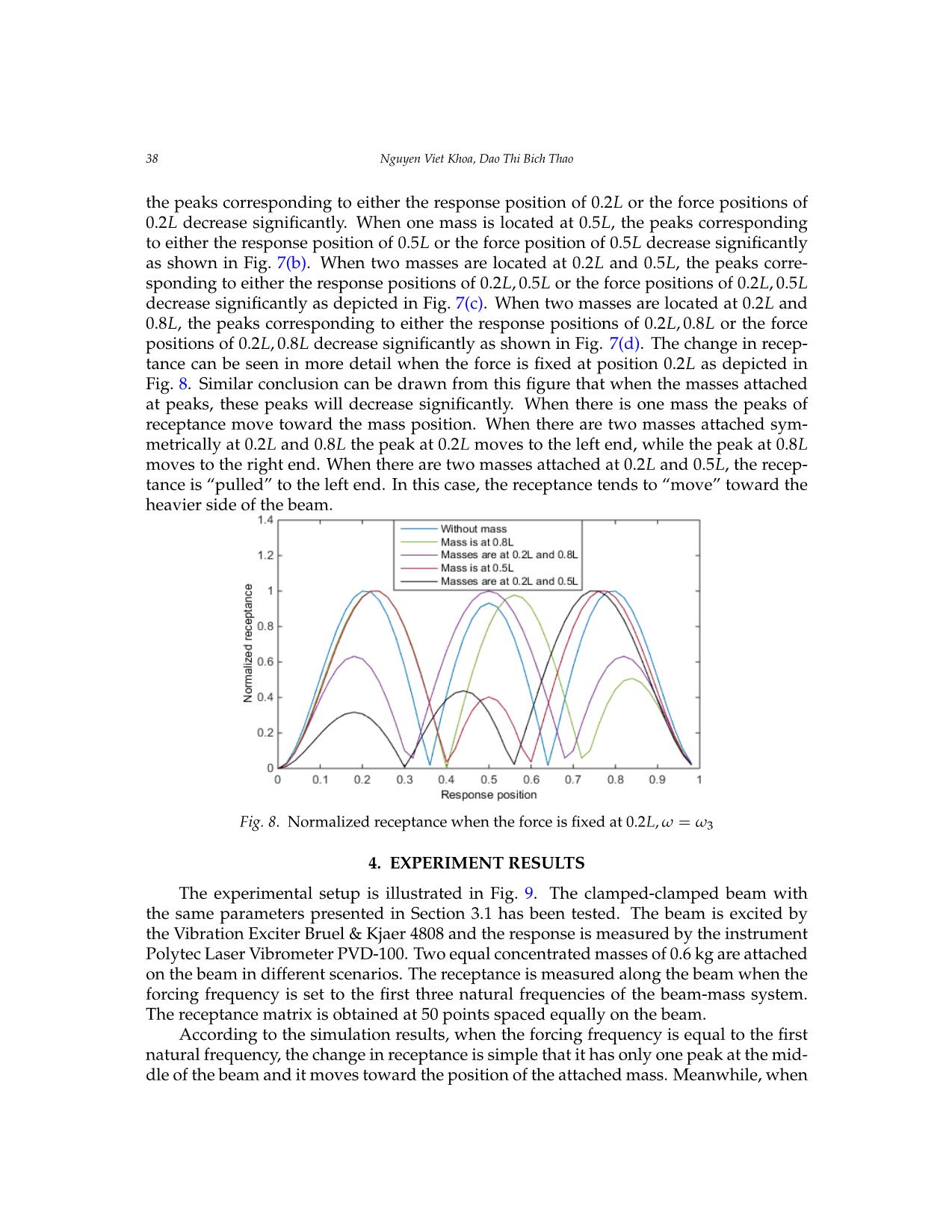
 Vietnam Journal of Mechanics, VAST, Vol.42, No. 1 (2020), pp. 29 – 42
 DOI: https://doi.org/10.15625/0866-7136/14628
 THEORETICAL AND EXPERIMENTAL ANALYSIS
 OF THE EXACT RECEPTANCE FUNCTION
 OF A CLAMPED-CLAMPED BEAM WITH
 CONCENTRATED MASSES
 Nguyen Viet Khoa1,∗, Dao Thi Bich Thao1
 1Institute of Mechanics, VAST, Hanoi, Vietnam
 E-mail: nvkhoa@imech.vast.vn
 Received: 13 November 2019 / Published online: 01 March 2020
 Abstract. This paper establishes the exact receptance function of a clamped-clamped beam
 carrying concentrated masses. The derivation of exact receptance and the numerical sim-
 ulations are provided. The proposed receptance function can be used as a convenient tool
 for predicting the dynamic response at arbitrary point of the beam acted by a harmonic
 force applied at arbitrary point. The influence of the concentrated masses on the recep-
 tance is investigated. The numerical simulations show that peak in the receptance will
 decrease when there is a mass located close to that peak position. The numerical results
 have been compared to the experimental results to justify the theory.
 Keywords: receptance, frequency response function, concentrated mass.
 1. INTRODUCTION
 The receptance function is very important in vibration problems such as control de-
sign, system identification or damage detection since it interrelates the harmonic excita-
tion and the response of a structure in the frequency domain. The receptance method
was first introduced by Bishop and Johnson [1]. This method has been developed and
applied widely in mechanical systems and structural dynamics. Milne [2] proposed a
general solution of the receptance function of uniform beams which can be applied for
all combinations of beam end conditions. Yang [3] derived the exact receptances of non-
proportionally damped dynamic systems. In this work an iteration procedure is devel-
oped based on a decomposition of the damping matrix, which does not require matrix
inversion and eliminate the error caused by the undamped model data. Lin and Lim [4]
proposed the receptance sensitivity with respect to mass modification and stiffness mod-
ification from the limited vibration test data. Mottershead [5] investigate the measured
zeros from frequency response functions and its application to model assessment and
updating. Gurgoze [6] presented the receptance matrices of viscously damped systems
 
c 2020 Vietnam Academy of Science and Technology
30 Nguyen Viet Khoa, Dao Thi Bich Thao
subject to several constraint equations. In this paper, the frequency response matrix of the
unconstrained system and the coefficient vectors of the constraint equations was used to
obtain the frequency response matrix of the constrained system. Gurg¨ oze¨ and Erol [7]
established the frequency response function of a damped cantilever simply supported
beam carrying a tip mass. In this paper, the frequency response function was derived
by using a formula established for the receptance matrix of discrete linear systems sub-
jected to linear constraint equations, in which the simple support was considered as a
linear constraint imposed on generalized co-ordinates. Burlon et al. [8] derived an ex-
act frequency response function of axially loaded beams with viscoelastic dampers. The
method relies on the theory of generalized functions to handle the discontinuities of the
response variables, within a standard 1D formulation of the equation of motion. In an-
other work, Burlon et al. [9] presented an exact frequency response of two-node coupled
bending-torsional beam element with attachments. Karakas and Gurg¨ oze¨ [10] extended
the work in [3] in which the receptance matrix was obtained directly without using the it-
erations as presented in [3] to form the receptance matrix of non-proportionally damped
dynamic systems. Muscolino and Santoro [11] developed the explicit frequency response
functions of discretized structures with uncertain parameters. Recently, the authors of
this paper [12] presented the exact formula of the receptance function of a cracked beam
and its application for crack detection. However, the exact form of frequency response
function of a beam with concentrated masses has not been established yet.
 The aim of the present paper is to present an exact receptance function of a clamped-
clamped beam carrying an arbitrary number of concentrated masses. The proposed for-
mula of receptance function is simple and can be applied easily to investigate the dy-
namic response of beam at an arbitrary point under a harmonic force applied at any
point along the beam. The influence of concentrated masses on the receptance of the
clamped-clamped beam is investigated. The comparison between numerical simulations
and experimental results have been carried out to justify the proposed method.
 2. THEORETICAL BACKGROUND
 Considering the Euler–Bernoulli beam carrying concentrated masses subjected to a
force ... ncy is equal to the first
obtainednatural at frequency, 50 points thespaced change equally in receptance on the beam. is simple that it has only one peak at the mid-
Accordingdle of the to beam the andsimulation it moves results, toward when the positionthe forcing of thefrequency attached is mass.equal Meanwhile,to the first natural when 
frequency, the change in receptance is simple that it has only one peak at the middle of the beam 
and it moves toward the position of the attached mass. Meanwhile, when the forcing frequency 
is high the change in receptance becomes more complicated with different configurations of the 
attached masses. Therefore, when the forcing frequency is equal to the first natural frequency 
 only the receptance curve extracted with the force fixed at one position is measured, while the 
 whole receptance matrices are measured at the second and third natural frequencies. 
 When the mass is attached at the position of L/4, the force is fixed at L/2 and the forcing 
 frequency is equal to the first natural frequency, the measured receptance moves to the left end 
 as presented in Fig. 9. Comparing Figs. 3 and 9 it is concluded that the measured receptance 
 and the simulation results are in very good agreement in both cases without and with an attached 
 mass. 
 When the excitation frequency is equal to the second natural frequency and the mas is attached 
 at the position of L/4, the measured receptance matrix presented in Fg. 4a and the simulation 
 receptance matrix shown in Fig. 10a are in very good agreement. As can be seen from Fig. 10a, 
 three peaks corresponding to the position of L/4 in the receptance matrix decrease significantly. 
 When the mass is attached at L/2 and the forcing frequency is equal to the third natural 
 frequency, five peaks of the receptance matrix corresponding to the position of L/2 decrease 
 significantly as can be observed in Fig. 10b. This agrees with the simulation result depicted in 
 Fig 6b. Fig. 11 presents the experimental receptance curves of beam without and with an 
 attached mass at L/4 which was measured when the forcing frequency is equal to the second 
 natural frequency. When there is no mass attached, these receptance has two peaks at L/4 and 
 3L/4. These experimental results justify the correctness of the simulation results presented in 
 Fig. 5. When there is a mass attached at the position of L/4, the peak at the mass position 
 decreases clearly. Fig. 12 presents the receptance measured when the force frequency is equal 
 to the third natural frequency. As can be seen from this figure, when there is no mass attached 
 the receptance has three peaks at L/6, L/2 and 5L/6. When there are masses attached, the 
 receptanceTheoretical andpeaks experimental decrease analysis significantly of the exact receptance at the function mass of a clamped-clamped positions. The beam experiment with concentratedal massesresults 39 
 presented in Fig. 12 are in very good agreement with the simulation results depicted in Fig. 7. 
 Fig. 8. Experimental setup 
 Fig. 9. Experimental setup
the forcing frequency is high the change in receptance becomes more complicated with
different configurations of the attached masses. Therefore, when the forcing frequency
is equal to the first natural frequency only the receptance curve extracted with the force
fixed at one position is measured, while the whole receptance matrices are measured at
the second and third natural frequencies.
 When the mass is attached at the position of L/4, the force is fixed at L/2 and the
forcing frequency is equal to the first natural frequency, the measured receptance moves
to the left end as presented in Fig. 10. Comparing Figs.4 and 10 it is concluded that the
measured receptance and the simulation results are in very good agreement in both cases
without and with an attached mass.
 1.2 Without mass With mass at 0.25L
 1
 0.8
 0.6
 0.4
 0.2
 Normalized receptance
 0
 0 0.2 0.4 0.6 0.8 1
 Response position 
 Fig. 9. Measured receptance curves of beam, force position=L/4, ω=ω1 
 Fig. 10. Measured receptance curves of beam, force position = L/4, ω = ω1
 a) b) 
 Fig. 10. Measured receptance matrices of beam: a) ω=ω2; b) ω=ω3 
 1.2 Without mass
 1 With mass at 0.25L
 0.8
 0.6
 0.4
 0.2
 Normalized receptance
 0
 0 0.2 0.4 0.6 0.8 1
 Response position 
 Figure 11. Measured receptance curves of beam, force position=L/4, ω=ω2 
 40 Nguyen Viet Khoa, Dao Thi Bich Thao
 When the excitation frequency is equal to the second natural frequency and the mas
 is attached at the position of L/4, the measured receptance matrix presented in Fig. 5(a)
 and the simulation receptance matrix shown in Fig. 11(a) are in very good agreement. As
 can be seen from Fig. 11(a), three peaks corresponding to the position of L/4 in the re-
 1.2
 ceptance matrix decrease1.2 significantly.WithoutWithout Whenmass mass theWith massWith mass mass is at attached 0.25Lat 0.25L at L/2 and the forcing
 frequency is equal1 to1 the third natural frequency, five peaks of the receptance matrix cor-
 responding to the position of L/2 decrease significantly as can be observed in Fig. 11(b).
 This agrees with0.8 the0.8 simulation result depicted in Fig. 7(b). Fig. 12 presents the experi-
 mental receptance0.6 curves0.6 of beam without and with an attached mass at L/4 which was
 measured when the forcing frequency is equal to the second natural frequency. When
 there is no mass attached,0.40.4 these receptance has two peaks at L/4 and 3L/4. These exper-
 1.2 Without mass With mass at 0.25L
 imental results justify0.2 the correctness of the simulation results presented in Fig.6. When
 Normalized receptance 0.2
 there1 is a mass attachedNormalized receptance at the position of L/4, the peak at the mass position decreases
 clearly.0.8 Fig. 13 presents0 0 the receptance measured when the force frequency is equal to the
 0 0 0.20.2 0.40.4 0.60.6 0.80.8 1 1
 third0.6 natural frequency. As can be seen from this figure, when there is no mass attached
 ResponseResponse position position 
 the0.4 receptance has three peaks at L/6, L/2 and 5L/6. When there are masses attached,
 Fig.Fig. 9. Measured9. Measured receptance receptance curves curves of ofbeam, beam, force force position= position=L/4L/4, ω, =ωω=ω1 1 
 0.2
 Normalized receptance
 0
 0 0.2 0.4 0.6 0.8 1
 Response position 
 Fig. 9. Measured receptance curves of beam, force position=L/4, ω=ω1 
 (a) ω = ω2 (b) ω = ω3
 a) a) b)b) 
 a) b) 
 Fig.Fig. 10 .1 Measured0. MeasuredFig. 11 .receptance Measured receptance receptancematrices matrices of matrices ofbeam beam: a) of: a)ω beam =ωω=2ω; 2b); b) ω =ωω=ω3 3 
 Fig. 10. Measured receptance matrices of beam: a) ω=ω2; b) ω=ω3 
 1.21.2
 1.2 WithoutWithout mass mass
 Without mass 1.2 Without mass
 WithWith mass mass at 0.25Lat 0.25L
 1 1 With1 mass at 0.25L Mass is at 0.5L
 1
 0.8
 0.80.8 0.8
 0.6
 0.60.6 0.6
 0.4
 0.4
 0.4
 0.2 0.4
 Normalized receptance 0.2
 Normalized receptance
 0 0.2
 0.2Normalized receptance
 Normalized receptance 0
 0 0.2 0.4 0.6 0.8 1
 0 0.2 0.4 0.6 0.8 1
 Response0 0 position Response position 
 0 0.2 0.4 0.6 0.8 1
Figure 11. Measured receptance curves0 of beam0.2, force position=0.4FigureL/4, ω 1=2ω. 0.6Measured2 receptance0.8 curves1 of beam, force position=L/6, ω=ω3 
 Fig. 12. Measured receptance curves of beam,ResponseFig. position 13. Measured receptance curves of beam,
 5. ConclusionResponse position 
 force position = L/4, ω = ω2 force position = L/6, ω = ω3
 FigureFigure 11 .1 Measured1. Measured receptance receptanceIn this curves paper, curves the of exact ofbeam beam receptance, force, force functionposition= position= of clampedL/4L/4, ω,- clampedω=ω=ω 2 beam carrying concentrated 
 masses is derived. The proposed receptance function can be 2applied easily for predicting the 
 response of the beam under a harmonic excitation. The influence of the concentrated masses on 
 the receptance of beam is also investigated. 
 When the excitation frequency is equal to a natural frequency, the peaks and nodes positions of 
 the receptance are the same with the maximum and minimum positions of the corresponding 
 mode shape. When there are concentrated masses the shape of receptance is changed. When the 
 mass positions are close to peaks of receptance, these peaks will decrease significantly. When 
 the masses are located at the nodes of receptance, the receptance is not influenced. The influence 
 of the masses on the receptance matrices can be used to control the vibration amplitudes at some 
 specific positions at given forcing frequencies. 
 The experiment has been carried out when the forcing frequency is set to the first three natural 
 frequencies of the beam carrying concentrated masses. The experimental and simulation results 
 are in very good agreement which justifies the proposed method. 
 Acknowledgements 
 This research is funded by Vietnam National Foundation for Science and Technology 
 Development (NAFOSTED) under grant number 107.02-2017.300. 
 References 
 [1] R.E.D. Bishop, D.C. Johnson, The Mechanics of Vibration, Cambridge University Press, 
 Cambridge, 1960. 
 [2] H.K. Milne, The receptance functions of uniform beams. Journal of Soundand Vibration 
 (1989) 131(3), 353-365. 
 [3] B. Yang, Exact receptances of nonproportionally damped systems, Transactions of 
 American Society of Mechanical Engineers Journal of Vibration and Acoustics 115 (1993) 47–
 52. 
 [4] R.M. Lin, M.K. Lim, Derivation of structural design sensitivities from vibration test data, 
 Journal of Sound and Vibration 201 (1997) 613–631. 
 [5] J.E. Mottershead, On the zeros of structural frequency response functions and their 
 sensitivities, Mechanical Systems and Signal Processing 12 (1998) 591–597. 
 [6] M. Gurgoze, Receptance matrices of viscously damped systems subject to several constraint 
 equations, Journal of Sound and Vibration (2000) 230(5), 1185-1190. 
 Theoretical and experimental analysis of the exact receptance function of a clamped-clamped beam with concentrated masses 41
the receptance peaks decrease significantly at the mass positions. The experimental re-
sults presented in Fig. 13 are in very good agreement with the simulation results depicted
in Fig.8.
 5. CONCLUSIONS
 In this paper, the exact receptance function of clamped-clamped beam carrying con-
centrated masses is derived. The proposed receptance function can be applied easily
for predicting the response of the beam under a harmonic excitation. The influence of
the concentrated masses on the receptance of beam is also investigated. When the ex-
citation frequency is equal to a natural frequency, the peaks and nodes positions of the
receptance are the same with the maximum and minimum positions of the correspond-
ing mode shape. When there are concentrated masses the shape of receptance is changed.
When the mass positions are close to peaks of receptance, these peaks will decrease sig-
nificantly. When the masses are located at the nodes of receptance, the receptance is not
influenced. The influence of masses on the receptance matrices can be used to control the
vibration amplitudes at some specific positions at given forcing frequencies.
 The experiment has been carried out when the forcing frequency is set to the first
three natural frequencies of the beam carrying concentrated masses. The experimental
and simulation results are in very good agreement which justifies the proposed method.
 ACKNOWLEDGEMENTS
 This research is funded by Vietnam National Foundation for Science and Technology
Development (NAFOSTED) under grant number 107.02-2017.300.
 REFERENCES
 [1] R. E. D. Bishop and D. C. Johnson. The mechanics of vibration. Cambridge University Press,
 (2011).
 [2] H. K. Milne. The receptance functions of uniform beams. Journal of Sound and Vibration, 131,
 (3), (1989), pp. 353–365. https://doi.org/10.1016/0022-460X(89)90998-X.
 [3] B. Yang. Exact receptances of nonproportionally damped dynamic systems. Journal of Vibra-
 tion and Acoustics, 115, (1), (1993), pp. 47–52. https://doi.org/10.1115/1.2930313.
 [4] R. M. Lin and M. K. Lim. Derivation of structural design sensitivities from vi-
 bration test data. Journal of Sound and Vibration, 201, (5), (1997), pp. 613–631.
 https://doi.org/10.1006/jsvi.1996.0836.
 [5] J. E. Mottershead. On the zeros of structural frequency response functions and their
 sensitivities. Mechanical Systems and Signal Processing, 12, (5), (1998), pp. 591–597.
 https://doi.org/10.1006/mssp.1998.0167.
 [6] M. Gurgoze. Receptance matrices of viscously damped systems subject to several
 constraint equations. Journal of Sound and Vibration, 230, (5), (2000), pp. 1185–1190.
 https://doi.org/10.1006/jsvi.1999.2602.
 [7]M.G urg¨ oze¨ and H. Erol. On the frequency response function of a damped cantilever simply
 supported in-span and carrying a tip mass. Journal of Sound and Vibration, 255, (3), (2002),
 pp. 489–500. https://doi.org/10.1006/jsvi.2001.4118.
42 Nguyen Viet Khoa, Dao Thi Bich Thao
 [8] A. Burlon, G. Failla, and F. Arena. Exact frequency response analysis of axially loaded beams
 with viscoelastic dampers. International Journal of Mechanical Sciences, 115, (2016), pp. 370–
 384. https://doi.org/10.1016/j.ijmecsci.2016.07.024.
 [9] A. Burlon, G. Failla, and F. Arena. Exact frequency response of two-node coupled bending-
 torsional beam element with attachments. Applied Mathematical Modelling, 63, (2018), pp. 508–
 537. https://doi.org/10.1016/j.apm.2018.06.047.
[10] A. Karakas and M. Gurg¨ oze.¨ A novel formulation of the receptance matrix of non-
 proportionally damped dynamic systems. Journal of Sound and Vibration, 264, (3), (2003),
 pp. 733–740. https://doi.org/10.1016/s0022-460x(02)01507-9.
[11] G. Muscolino, R. Santoro, and A. Sofi. Explicit frequency response functions of dis-
 cretized structures with uncertain parameters. Computers & Structures, 133, (2014), pp. 64–78.
 https://doi.org/10.1016/j.compstruc.2013.11.007.
[12] N. V. Khoa, C. Van Mai, and D. T. B. Thao. Exact receptance function and receptance curva-
 ture of a clamped-clamped continuous cracked beam. Vietnam Journal of Mechanics, 41, (4),
 (2019), pp. 349–361. https://doi.org/10.15625/0866-7136/14566.
[13] J. S. Wu and T. L. Lin. Free vibration analysis of a uniform cantilever beam with point masses
 by an analytical-and-numerical-combined method. Journal of Sound and Vibration, 136, (2),
 (1990), pp. 201–213. https://doi.org/10.1016/0022-460X(90)90851-P.
[14] S. Maiz, D. V. Bambill, C. A. Rossit, and P. A. A. Laura. Transverse vibration of
 Bernoulli–Euler beams carrying point masses and taking into account their rotatory in-
 ertia: Exact solution. Journal of Sound and Vibration, 303, (3-5), (2007), pp. 895–908.
 https://doi.org/10.1016/j.jsv.2006.12.028.