The effect of ni replacement with ge on the magnetic properties of LaNi₅ alloy

ISSN 2354-0575
 THE EFFECT OF Ni REPLACEMENT WITH Ge
 ON THE MAGNETIC PROPERTIES OF LaNi5 ALLOY
 Dam Nhan Ba
 Hung Yen University of Technology and Education
 Received: 10/01/2020
 Revised: 15/02/2020
 Accepted for publication: 25/02/2020 
Abstract:
 In this paper, we present the results of the study on the magnetic properties of LaNi5-xGex (x = 0.1 - 
0.5) alloys based on extending the Langevin’s classical theory of paramagnetism. The calculation results 
show that the number of magnetic particles decreases and the size of magnetic particles increases as the 
concentration of Ge in LaNi5 alloy increases. The LaNi5-xGex alloy after charge/discharge changes from 
paramagnetic to super paramagnetic. The calculated data is verified by making joints by the Langevin’s 
function according to the M-H data at room temperature, the results of matching between the theoretical 
line and the experimental data are over 99%. This study gives us a better understanding of the processes 
that occur when Ni-MH rechargeable battery is charged/discharged.
Keywords: Absorption of hydrogen, LaNi5 , Ni-MH rechargeable battery, Magnetic properties.
1. Introduction surfaces. However, photoelectron spectroscopy 
 The intermetallic compound (IMC) LaNi5 studies “0” on cycled powder electrodes of both 
is well known for its ability to store hydrogen LaNi5-xSix and LaNi5-xAlx did not indicate the 
reversibly at pressures and temperatures of interest presence of these solute-enriched surface oxide 
for applications close to ambient conditions [1, films. However, good cycling properties are also
2]. However, long-term cycling leads to severe obtained with Ge-substituted compounds [15]. 
degradation of the material [3, 4]. To overcome When doped Ge into LaNi5 alloy, the current density 
this problem, substitutions have been performed on is increased by 10 times compared to the original 
the Ni sites, leading to pseudo-binary compounds LaNi5 alloy and other doped elements, meaning 
LaNi5−xMx (M = Al, Sn, Mg, Fe, Co) with improved that the maximum current capacity of the battery 
resistance towards degradation [5-9]. The most increases by 10 times. This is interesting because 
important result of alloy substitution for the Ge is a semiconductor element (group IV in the 
extension of cycle life is thought to be a reduction periodic table).
in volume expansion upon hydride formation. Co In this study, we use the Langevin’s 
substitution for Ni has been identified as one of the classical theory of paramagnetism to calculate the 
most effective solutes in this respect and results in a concentration of magnetic particles, the size of 
greatly reduced tendency toward fragmentation and the magnetic particles and the paramagnetic shell. 
corrosion leading to batteries with long lifetimes Consequently, it serves as a reference compound to 
[10, 11]. Unfortunately, cobalt is an expensive understand the physical and chemical phenomena 
element, and the specific role of Co is not well influencing the hydrogenation properties. 
understood. Particularly, it has been shown that Sn 
significantly enhances the stability of the hydride 2. Theory
during temperature cycling [12, 13]. Meli [14] First we have to look back at Langevin’s 
has speculated that Si and Al substitutions inhibit classical theory of paramagnetism [16]. Langevin 
corrosion during electrochemical cycling through (1905) considered the system of N atoms to have 
the formation of passivating oxide films on the a magnetic moment μ placed far enough apart to 
74 Khoa học & Công nghệ - Số 25/Tháng 3 - 2020 Journal of Science and Technology
 ISSN 2354-0575
not interact with each other. It is known that the . a
 3 . Thus, when a is very small, the Langevin’s 
magnetization M of the system and the free energy function is a straight line creating an α angle with 
F are related by the Formula: the horizontal axis.
 =- 2F
 M 2 (1) dL 1
 H / tan c = 3 (13)
 Here blda a % 1
 =- The experiment is performed at room 
 FNkB TlnZ (2)
 For a statistical Z value: temperature in the laboratory’s normal magnetic 
 Ei 6
 - field. If taking μ ~ 1μ , H ~ 10 A/m = 12600 Oe. 
 Ze= / kTB (3) B
 We have: μH = μ H = 1.17x10-29 Wbm x 106 A/m = 
 The potential U of each atom in the magnetic B
 -23 
field H is determined by the Formula: 1.17 x 10 J. At room temperature corresponds to 
 k T = 1.38 x 10-23 J/K x 300 K = 4.1 x 10-21 J.
 UH=-nnv.cv =- H os i (4) B
 Whereas θ is the angle between nv and Hv . Therefore:
 µ H 1.17× 10−23
 Using Formula (3) to calculate Z, in addition =B = =× −3 <<
 a −21 2.8 1 0 1 
 kTB 4.1× 10
to replacing U from Formula (4) for Ei, we replace 
the ∑ symbol with the ∫ symbol because in the Then we can replace L(a) by a/3. From (11) 
 and (12) equation we get:
classical model, the magnetic moment is oriented 2
 Nµ 
any θ and { possible continuous change. We get: MH= (14)
 2ππ 3kT
 µθH cos B
 Zd=∫∫ϕ = esinθθd (5) The maximum magnetic moment is obtained 
 kT
 00B at the maximum magnetic field. From this we know 
 Add the symbols: the value of the magnetic moment and from the 
 nH
 a = and x = cos i (6) value of the magnetic moment we calculate χ by the 
 kTB Formula:
 2
 We have: MNµ 
 + χ = = (15)
 1 π
 ax 4 H3 kT
 z=2π ∫ e dx = sha (7) B
 −1 a
 3. Results and discussion
 Using the Formulas (1) - (3), we have:
 4r 3.1. Calculation of the number of magnetic 
 FN=- kTln sha (8)
 B aka particles
 11
 = a - + 2a According to Langevin’s classical theory of 
 MNkTB 2 a cha 2H
 sha bla paramagnetic, we see that at low temperatures, L 
 1
 = - 2a (a) → 1, (corresponding to large values of a), that 
 MNkTB ctha a 2H (9)
 ak LaNi Ge
 is, I has saturation values. We study 5-xx 
 Because: material, because the material is placed in a 
 ∂a µ
 = (10) magnetic field in the range of -15 kOe 15 kOe,
 ∂
 H kTB and at room temperature, so the value of a is not 
 So that: large. Moreover, in the Langevin’s classical theory 
 MN= nLa (11) of paramagnetic, we consider the atomic N system 
 _i
 With: to be non-interacting. For LaNi Ge materials, the 
 1 5-x x
 L( a) = cth( a) − ( 1 2 ) size of the material particles is from a few tens of 
 a nanometers to hundreds of nanometers, meaning 
 L(a) is called the Langevin’s function. that a single particle can contain thousands to tens 
 1
 ""01, " 0 nH
 When acth a and a , so that of thousands of atoms. So in a = Formula we 
 _i kTB
 La " 1. Thus, when a is very large, the Langevin’s 
 _i have to replace μB by μ, where μ is worth thousands 
function is asymptotic to the value L(a) = 1. to tens of thousands of μ .
 1 a B
 When a % 1, cth( a) ≈+, so that L(a) Assuming μ = 103μ , infer a = 2.8. According 
 a 3 B
Khoa học & Công nghệ - Số 25/Tháng 3 - 2020 Journal of Science and Technology 75
ISSN 2354-0575
to the Formulas (11) and (12) we have: 3.2. Calculate the paramagnetic shell size of the 
 = M particles
 N n (/- 1 ) (16)
 ctha a As above, we have calculated the number of 
 nH
 Plug the values for a = and MH= | into magnetic particles per unit volume. We assume 
 kTB
the Formula (16) we have: that the particle has a spherical shape, lying close 
 χ H together. We can then consider the total volume 
 N = (17) of all particles per 1 volume unit to be equal to 1 
 µH k T 
 µ cth − B  volume unit.
 kTµ H
 B   Because the number of particles is measured 
 We take H value from the laboratory’s in units of particles/m3, so we have:
 6 413 
magnetic field, H = 12600 Oe ≈ 10 A/m. For LaNi5 π R = (18)
materials, in Table 1 we have χ = 3.7 x 10-6. 3 N
 Therefore, M = 3.7 A/m. Plug these values Inferred:
 3
into the Formula (17) we have: R = 3 (19)
 37./ 4π N
 = Am
 N -26 -
 11.(71##02Wbmcth ./8128.) With the N values in Table 1 and as calculated 
 19 3
 Nm= 61 # 10 particles/ by Formula (19), we get the magnetic particle radius 
 _i
 of the alloys as follows:
Table 1: The number of N-magnetic particles depends 
 Table 2: Dependence of R particle size on Ge 
 on the concentration of Ge in LaNi5-xGex alloys
 concentration in LaNi5-xGex alloys
 N x 1019 
 No. Samples χ (10-6) N x 1019 
 (particles/m3) No. Samples R(nm)
 (particles/m3)
 1 LaNi5 3,700 61
 1 LaNi5 61 73,1
 2 LaNi4.9Ge0.1 2,819 46
 2 LaNi4.9Ge0.1 46 80,3
 3 LaNi4.8Ge0.2 2,530 42
 3 LaNi4.8Ge0.2 42 82,8
 4 LaNi4.7Ge0.3 2,147 35
 4 LaNi4.7Ge0.3 35 88,0
 5 LaNi4.6Ge0.4 1,724 28
 5 LaNi4.6Ge0.4 28 94,8
 6 LaNi4.5Ge0.5 1,409 23
 6 LaNi Ge 23 101,2
 Similarly, the values of χ for the material 4.5 0.5
LaNi5-xGex (x = 0.1 - 0.5), we also obtained the The results in Table 2 show that when doped 
values of N, the results are shown in Table 1. Ge is added to LaNi5 alloy, the size of magnetic 
 Table 1 shows that if Ge element is doped into particles increases.
 3
LaNi5 alloy, the number of magnetic particles will We have assumed above: μ = 10 μB, that is, 
decrease. we assume that the particle has a magnetic moment 
 Because element Ge belongs to group IV of 1,000 times the atomic magnetic moment. So if 
the periodic table (non-magnetic element), when the particle is about 10 atomic dimensions, that 
doped, it will replace Ni particles (ferromagnetic is, the particle contains about 103 atoms, then the 
element), and reduce the number of Ni magnetic magnetic moments of the atom in that particle must 
particles. be arranged in parallel. That is, the particle then has 
 According to Equation (17), we see that the structure of a single domain.
N is linearly dependent on χ and the number of We know that for a nanoparticle with a 
magnetic particles is inversely proportional to the diameter of 5 nm, the number of atoms that it 
concentration of Ge element added. As the number contains is 4,000 atoms. However, as the results 
of magnetic particles decreases, the magnetic have calculated, it is found that the size of the 
moment of the sample also decreases. particle is very large, so each particle can contain 
76 Khoa học & Công nghệ - Số 25/Tháng 3 - 2020 Journal of Science and Technology
 ISSN 2354-0575
up to tens of thousands of atoms. So why does the 3
 MdSρπ ( mag /6) H
particle have only magnetic moments equal to 103 x = (21)
 kTB
atomic magnetic moments?
 Here:
 This can be explained logically if the particle 
 M is the saturation magnetic moment in units 
is made up of two components, the kernel and the S
 of emu/g
shell. The kernel includes the magnetic moment of 
 r d3 / 6 is the average volume of magnetic 
atoms arranged in parallel with each other, while the `jmag
 particles
shell consists of chaotic atoms. In other words, the 
 χ is the linear magnetic susceptibility showing 
magnetic moment in the kernel arranges the same as 
 the distribution of diamagnetism, magnetic 
that of ferromagnet, while the magnetic moment in 
 impurities and chaotic spins at the particle surface 
the shell is arranged like in paramagnetic. Because 
 causing the signal in the high magnetic field to be 
the magnetic moment in the shell is chaotic, it 
 distorted
creates a demagnetizing field that reduces the 
 ρ is the mass density of particles
magnetization of the particle.
 Mass density is determined by the formula:
 Because the size of the particle we calculate 
 8M
 ρ =
is about 50nm, the size of the kernel cannot be 3
 NaA
larger than 25nm, that is, it cannot be greater than 
 With: M is the molar mass measured by grams; 
½ of the particle size, because if the nucleus is 
 a is the lattice constant; N is the Avogadro constant.
larger than ½ of the particle size, then that particle A
will have a fairly large magnetic moment. If the 
demagnetization field of the paramagnetic shell is 
taken into account, the size of the nucleus can be 
estimated from 5nm to 25nm.
 In the Langevin’s classical theory of 
paramagnetism, we must consider a system of 
N atoms that do not interact with each other. In 
order to apply the Langevin’s classical theory of 
paramagnetism in this case, the two particles must 
not interact with each other. Because the magnetic 
moment of a particle is determined by the kernels, 
the interaction between the two particles as well Figure 1. The magnetization curve of the sample 
as the decision of the kernels. Because the kernel 
 LaNi5 after 10 charge/discharge cycles is matched 
size is small compared to the particle size, even if according to the Langevin’s function
we assume that the particles are close together, the 
distance between the two kernels will be greater Figure 1 shows the magnetization curves of 
than or equal to the particle size, then the interaction samples LaNi5 be fitted in the Langevin’s function 
between particles is negligible. (symbol ■ represents an experimental data line, 
 represents a line fitted by the Langevin’s function). 
3.3. Checking the paramagnetic properties by The data shown in Figure 1 shows the experimental 
the Langevin’s function and fitting lines of Langevin’s function with a joints 
 When the sample was in the superparamagnetic above 99%. This result confirms that the samples 
state, the magnetization curve consistent with were in powder state and the samples were charge/
the Langevin’s function was corrected for high- discharge after 10 cycles in superparamagnetic 
temperature induction [17]. states. The concentration of magnetic particles and 
 the size of the magnetic particles are determined 
 1 
 M( T , H )= AM .S  coth(x) −+χ H (20)
 x based on the experimental curve fitted according 
 With: to Langevin’s function according to Formula (20), 
Khoa học & Công nghệ - Số 25/Tháng 3 - 2020 Journal of Science and Technology 77
ISSN 2354-0575
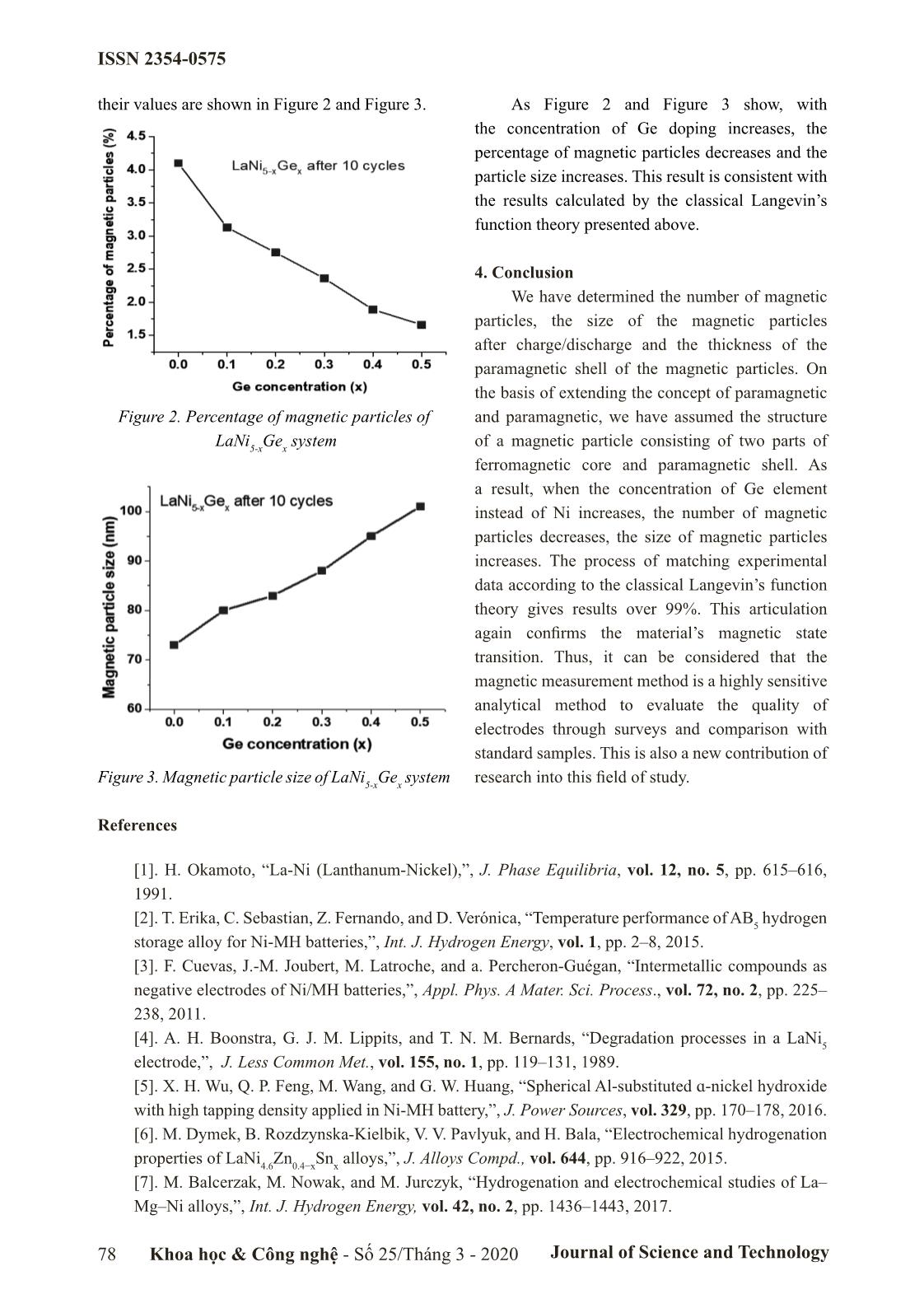
their values are shown in Figure 2 and Figure 3. As Figure 2 and Figure 3 show, with 
 the concentration of Ge doping increases, the 
 percentage of magnetic particles decreases and the 
 particle size increases. This result is consistent with 
 the results calculated by the classical Langevin’s 
 function theory presented above.
 4. Conclusion
 We have determined the number of magnetic 
 particles, the size of the magnetic particles 
 after charge/discharge and the thickness of the 
 paramagnetic shell of the magnetic particles. On 
 the basis of extending the concept of paramagnetic 
 Figure 2. Percentage of magnetic particles of and paramagnetic, we have assumed the structure 
 LaNi5-xGex system of a magnetic particle consisting of two parts of 
 ferromagnetic core and paramagnetic shell. As 
 a result, when the concentration of Ge element 
 instead of Ni increases, the number of magnetic 
 particles decreases, the size of magnetic particles 
 increases. The process of matching experimental 
 data according to the classical Langevin’s function 
 theory gives results over 99%. This articulation 
 again confirms the material’s magnetic state 
 transition. Thus, it can be considered that the 
 magnetic measurement method is a highly sensitive 
 analytical method to evaluate the quality of 
 electrodes through surveys and comparison with 
 standard samples. This is also a new contribution of 
Figure 3. Magnetic particle size of LaNi5-xGex system research into this field of study.
References
 [1]. H. Okamoto, “La-Ni (Lanthanum-Nickel),”, J. Phase Equilibria, vol. 12, no. 5, pp. 615–616, 
 1991.
 [2]. T. Erika, C. Sebastian, Z. Fernando, and D. Verónica, “Temperature performance of AB5 hydrogen 
 storage alloy for Ni-MH batteries,”, Int. J. Hydrogen Energy, vol. 1, pp. 2–8, 2015.
 [3]. F. Cuevas, J.-M. Joubert, M. Latroche, and a. Percheron-Guégan, “Intermetallic compounds as 
 negative electrodes of Ni/MH batteries,”, Appl. Phys. A Mater. Sci. Process., vol. 72, no. 2, pp. 225–
 238, 2011.
 [4]. A. H. Boonstra, G. J. M. Lippits, and T. N. M. Bernards, “Degradation processes in a LaNi5 
 electrode,”, J. Less Common Met., vol. 155, no. 1, pp. 119–131, 1989.
 [5]. X. H. Wu, Q. P. Feng, M. Wang, and G. W. Huang, “Spherical Al-substituted ɑ-nickel hydroxide 
 with high tapping density applied in Ni-MH battery,”, J. Power Sources, vol. 329, pp. 170–178, 2016.
 [6]. M. Dymek, B. Rozdzynska-Kielbik, V. V. Pavlyuk, and H. Bala, “Electrochemical hydrogenation 
 properties of LaNi4.6Zn0.4−xSnx alloys,”, J. Alloys Compd., vol. 644, pp. 916–922, 2015.
 [7]. M. Balcerzak, M. Nowak, and M. Jurczyk, “Hydrogenation and electrochemical studies of La–
 Mg–Ni alloys,”, Int. J. Hydrogen Energy, vol. 42, no. 2, pp. 1436–1443, 2017.
78 Khoa học & Công nghệ - Số 25/Tháng 3 - 2020 Journal of Science and Technology
 ISSN 2354-0575
 [8]. A. Sobianowska-Turek, “Hydrometallurgical recovery of metals: Ce, La, Co, Fe, Mn, Ni and Zn 
 from the stream of used Ni-MH cells,”, Waste Manag., vol. 77, no. April 2009, pp. 213–219, 2018.
 [9]. K. Lota et al., “Electrochemical properties of modified negative electrode for Ni-MH cell,”,Curr. 
 Appl. Phys., vol. 20, no. 1, pp. 106–113, 2020.
 [10]. M. Landa-Castro, J. Aldana-González, M. G. Montes de Oca-Yemha, M. Romero-Romo, E. M. 
 Arce-Estrada, and M. Palomar-Pardavé, “Ni–Co alloy electrodeposition from the cathode powder of 
 Ni-MH spent batteries leached with a deep eutectic solvent (reline),”, J. Alloys Compd., vol. 830, pp. 
 1–9, 2020.
 [11]. P. Bäuerlein, C. Antonius, J. Löffler, and J. Kümpers, “Progress in high-power nickel–metal 
 hydride batteries,”, J. Power Sources, vol. 176, no. 2, pp. 547–554, 2008.
 [12]. R. C. Ratnakumar, B. V. Witham, C. Bowman, Jr., “Electrochemical Studies on LaNi5-xSnx Metal 
 Hydride Alloys,”, J. Electrochem. Soc., vol. 143, no. 8, pp. 2578–2584, 1996.
 [13]. E. M. Borzone, A. Baruj, M. V. Blanco, and G. O. Meyer, “Dynamic measurements of hydrogen 
 reaction with LaNi5-xSnx alloys,”, Int. J. Hydrogen Energy, vol. 38, no. 18, pp. 7335–7343, 2013.
 [14]. F. Meli, A. Zuettel, and L. Schlapbach, “Surface and Bulk Properties of LaNi5-xSix Alloys from 
 the Viewpoint of Battery Applications.,”, J. Alloys Compd., vol. 190, no. 1, pp. 17–24, 1992.
 [15]. C. Witham, “Electrochemical Properties of LaNi5−xGex Alloys in Ni-MH Batteries,”, J. 
 Electrochem. Soc., vol. 144, no. 11, p. 3758-3764, 1997.
 [16]. F. R. Buschow, K.H.J, de Boer, Physics of Magnetism and Magnetic Materials. Kluwer Academic 
 / Plenum Publishers, 2004.
 [17]. Cullity, B.D., Introduction to Magnetic Materials. Addinson Wesley, New York, 1972.
 ẢNH HƯỞNG CỦA VIỆC THAY THẾ MỘT PHẦN Ni BẰNG Ge
 LÊN TÍNH CHẤT TỪ CỦA HỢP KIM LaNi5
Tóm tắt:
 Trong bài báo này, chúng tôi trình bày những kết quả nghiên cứu về tính chất từ của hệ vật liệu 
 LaNi5-xxGe (x = 0,1 ÷ 0,5) trên cơ sở mở rộng lý thuyết thuận từ của Langevin. Các kết quả tính toán cho 
thấy rằng số hạt từ giảm còn kích thước hạt từ tăng khi nồng độ Ge trong hợp kim LaNi5 tăng. Vật liệu 
LaNi5-xGex sau phóng/nạp chuyển từ trạng thái thuận từ sang trạng thái siêu thuận từ. Số liệu tính toán 
được kiểm lại bằng cách làm khớp bằng hàm Langevin theo số liệu M-H tại nhiệt độ phòng, kết quả làm 
khớp giữa đường lý thuyết và số liệu thực nghiệm đạt trên 99%. Nghiên cứu này giúp ta hiểu sâu sắc hơn 
các quá trình xảy ra khi phóng/nạp của pin nạp lại Ni-MH.
Từ khóa: Hấp thụ Hiđrô, LaNi5 , pin nạp lại Ni-MH, tính chất từ.
Khoa học & Công nghệ - Số 25/Tháng 3 - 2020 Journal of Science and Technology 79