The complex fluctuation conductivity in high-Tc superconductor at zero magnetic field

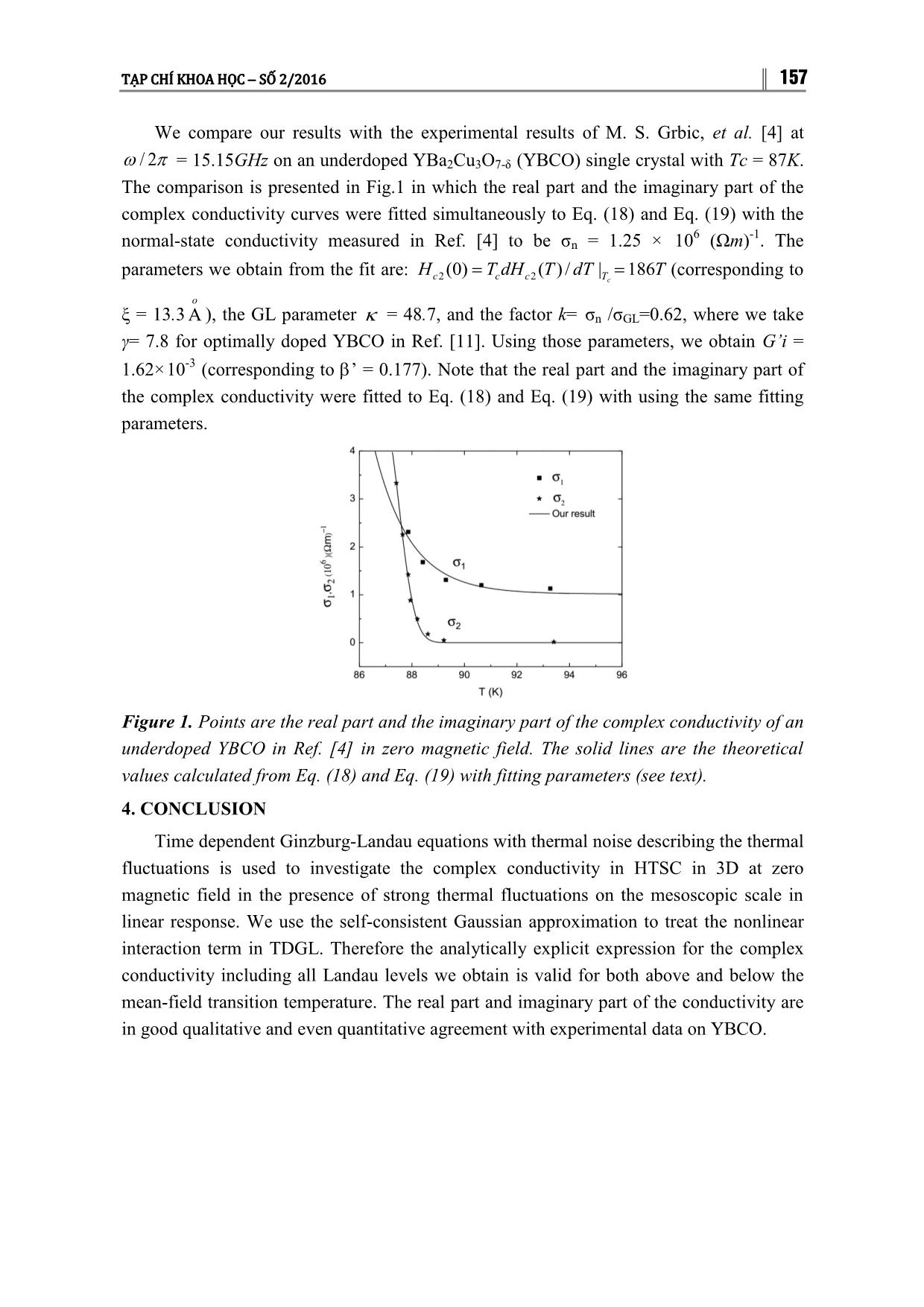
152 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
THE COMPLEX FLUCTUATION CONDUCTIVITY IN HIGH-TC 
 SUPERCONDUCTOR AT ZERO MAGNETIC FIELD 
 Bui Duc Tinh1, Pham Gia Hien, Le Minh Thu, Nguyen Quang Hoc 
 Hanoi National University of Education 
 Abstract: The time-dependent Ginzburg-Landau (TDGL) equation with thermal noise is 
 used to calculate the complex fluctuation conductivity in high-Tc superconductor in three 
 dimensional (3D) model at zero magnetic field. The nonlinear interaction term in the 
 TDGL is treated within self-consistent Gaussian approximation we go beyond the often 
 used lowest Landau level approximation. The expressions of the complex fluctuation 
 conductivity including all Landau levels is presented in explicit form which is applicable 
 essentially to both temperature above and below Tc. Our results are in good agreement 
 with experimental data on high- Tc superconductor YBa2Cu3O7-δ . 
 Keywords: Complex conductivity; High-Tc superconductors; Ginzburg-Landau equation 
1. INTRODUCTION 
 The investigation of thermal fluctuation on complex conductivity in strongly high-Tc 
superconductors (HTSC) have been a subject for active research for many years, mainly 
due to discovery of the HTSC in which the effects are enhanced by the short coherence 
length and the anisotropy and high-Tc. The fluctuation conductivity was calculated by 
Aslamasov and Larkin in the framework of the microscopic (BCS) theory [1], the 
calculation fast becomes too cumbersome in more complicated situations involving 
external magnetic field, layered structure etc and a more phenomenological Ginzburg- 
Landau approach is more effective. In the Gaussian fluctuations regime (ignoring the 
nonlinear interaction term in the TDGL for above the mean-field transition temperature), 
the formulas for the superconducting complex fluctuation conductivity in the normal phase 
at zero magnetic field have been very early obtained within the TDGL equation [2]. 
1 Nhận bài ngày 20.12.2015, gửi phản biện và duyệt đăng ngày 25.01.2016. 
 Liên hệ tác giả: Bùi Đức Tĩnh; Email: bdtinh@hnue.edu.vn. 
TẠP CHÍ KHOA HỌC SỐ 2/2016 153 
 In this paper we will calculate the complex fluctuation conductivity including all 
Landau levels in a 3D superconductor at zero magnetic field by using TDGL approach 
with thermal fluctuations conveniently modeled by the Langevin white noise. The 
nonlinear interaction term in the TDGL is treated in self-consistent Gaussian 
approximation. A main contribution of our paper is an explicit form of the Green function 
incorporating all Landau levels. One of the main result of our work is that analytically 
explicit expression for the complex fluctuation conductivity at zero magnetic field is 
applicable essentially to both above and below the mean-field transition temperature 
(unlike Ref. [1]). The result is compared with experimental data [4] on YBa2Cu3O7-δ 
(YBCO). 
2. THEORY 
2.1. The Ginzburg - Landau Model in 3D 
 We can start with the Ginzburg - Landau (GL) free energy in 3D at zero magnetic 
field: 
 22
 hh2 2 2b 4
 F d3 r    a   , (1) 
 GL * z
 2mm 2c 2
 mf mf mf
 We assume linear dependence a = αTc (t −1), t ≡ T/Tc . The “mean field” critical 
 mf
temperature Tc depends on UV cutoff, τc, of the “mesoscopic” or “phenomenological” GL 
description, specified later. Effective Cooper pair mass in the ab plane is m* (disregarding 
for simplicity the anisotropy between the crystallographic a and b axes) while along the c 
 2 2 *
axis it is much larger mc. The two scales, the coherence length ξ =  /(2 m αTc); and the 
 2 2 * *2
penetration depth,  c m b'/(4 e Tc ) define the GL ratio    / , which is very large 
for HTSC. The electric current, J=Jns J , includes both the Ohmic normal part: 
 JEnn  , (2) 
and the supercurrent: 
 *
 ie h **
 JD-Ds *     . (3) 
 2m
 In order to study transport phenomena in superconductor, one uses the time dependent 
Ginzburg-Landau (TDGL) equation [5,6]: 
 *
 1  e  FGL
 0 i   *  , (4) 
 h
154 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
  1
where 0 is the order parameter relaxation time [7],  E()y is the scalar electric 
potential describing the driving force in a purely dissipative dynamics. The electric field is 
coordinate independent but is a monochromatic periodic function of time 
E( ) Eexp i . 
 Throughout most of the paper we use the coherence length ξ as a unit of length and 
 2
Hc2 0 / 2  as a unit of the magnetic field. In analogy to the coherence length and the 
penetration depth, one can define a characteristic time scale. In the superconducting phase 
 * 1 2 2
a typical “relaxation” time is GL m 0 / h . It is convenient to use the following unit 
of the electric field and the dimensionless field: EGL Hc2 / c GL , ()()/  EE  GL . The 
TDGL Eq. (4) written in dimensionless units reads: 
 2 2 2 mf
 1  1  1 t 1 2
 2 2 2 iyε( )  . (5) 
  2 x 2  y 2  z 2
 22mf
 The order parameter field and the thermal noise were rescaled:  2 Tbc / ' , 
 mf 3/2 1/2 mf
 (2 Tbc ) / . The “mean field” critical temperature Tc depends on UV cutoff. 
This temperature is higher than measured critical temperature Tc due to strong thermal 
fluctuations on the mesoscopic scale, and it will be renormalized later. The Langevin 
white-noise forces  are correlated through *(r,  )  (r',  ') 2 tmf  (r-r')  (   ') 
 1 2 2mf 2 2 2
with  2Gi , where the Ginzburg number is defined by Gi 8/ e  Tc c h 
 2
 2 *
with  m / mc being an anisotropy parameter. The dimensionless current density is 
 Js JGL js where 
 i **
 js ( D   D  ), (6) 
 2 
 2
with JGL cH2 c / (2 ) being the unit of the current density. Consistently the 
 22
conductivity will be given in units of GL J GL/ E GL c  ' / (4  ) . This unit is close to 
the normal state conductivity n in dirty limit superconductors [8]. In general there is a 
factor k of order one relating the two: σn = kσGL. 
2.2. The self-consistent Gaussian approximation 
TẠP CHÍ KHOA HỌC SỐ 2/2016 155 
 The cubic term in the TDGL Eq. (5) will be treated in the self-consistent Gaussian 
 2
approximation [9] by replacing 2 with a linear one 2 
 1 2 1  2 1  2
 2 2 2 ar  ,
  2 x 2  y 2  z (7) 
leading the “renormalized” value of the coefficient of the linear term: 
 mf
 t 1 2
 a 2 . (8) 
 r 2
 The relaxational linearized TDGL equation with a Langevin noise, Eq. (7), is solved 
 0 0
using the retarded (G for τ<τ’) Green function (GF) G k z (r,;r',') : 
 dk
 (,)r  z e ikz z d r ' d  ' G0 (,;',')(,) r  r   r  . (9) 
 2 kkzz
 The GF satisfies: 
 222
 11   kz 0
 22 aGrk(r , r ';  ')  ( r r ')  (   ') . (10) 
  2 xy 2  2 z
 The solution of Eq. (10) is: 
 2 22
 0 1 kz XY 
 Gakr(rr , '; '')  (  '')exp  ''  '' , (11) 
 z 2  2 2 ''
 with X x x', Y y y ', ''   '.  (  '')is the Heaviside step function. 
 The thermal average of the superfluid density in 3D (density of Cooper pairs) can be 
expressed via the Green functions. 
 mf
 2 2 t 1
  (,)2r   tmf G0 (,';'')' r r  d  2 a .
 krz 2 3/2 
 '' c c (12) 
 The critical temperature Tc is defined as 
 2'
 TTmf 1, (13) 
 cc 3
 c
 1 2 2 2 2 2
 where  ' 2Gi ' with Gi' 8 e  Tc / c h . 
 2
 Then Eq. (8) can be solved for ar : 
156 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 1  '2t 2 2  ' t  ' 2 t 2
 a t 1 t 1 , (14) 
 r 22 
 2 2 4 
 mf
where t T/ Tc and note that tt ' . 
3. THE COMPLEX CONDUCTIVITY AT ZERO MAGNETIC FIELD 
3.1. Theoretical calculation 
 We can express the supercurrent density, defined by Eq. (6), via the Green functions 
as following: 
 dk 
 js ()(,,)(,,)., i  tz e ikz z dr'''' d  G r r''   G r r   c c (15) 
 y 2 kzzy k
where G (r,r', -') as the Green function of the linearized TDGL Eq. (5) in the presence 
 kz
of the scalar potential. One finds correction to the Green function to linear order in the 
electric field: 
 0 0
 G (r,r', '') G (r,r', '') i dr d 'G (r,r , ' ) (τ1) yG1k (r 1 ,r' , ' 2 ), (16) 
 kz k z 1 1 k z 1 1 z
where (τ1) are the scalar electric potential and electric field in dimensionless units 
respectively, 1'  1 , and  2 ' 1  '. 
 Substituting the full Green function (16) into expression (15), then doing the Fourier 
transform this current with respect to frequency one then obtains complex conductivity: 
 j()
 ()()()    i   , (17) 
 s () 12
 Where: 
 3/4
 't 2 2 22 3 
 1(  ) 2  2aarr 4  cos arctan , (18) 
 8  3 2 2a
  r
 3/4
 't 222 3 
 2 (  ) 2  2aarr  4  sin arctan . (19) 
 8  3 2 2a
  r
 The result (18) and (19) are consistent with the results of Larkin and Varlamov [1] if 
quartic term, |Ψ|4, in GL free energy is neglected for for above the mean-field transition 
temperature. Our results are applicable essentially to both above and below the mean-field 
transition temperature. 
3.2. Comparison with experiment 
TẠP CHÍ KHOA HỌC SỐ 2/2016 157 
 We compare our results with the experimental results of M. S. Grbic, et al. [4] at 
 / 2 = 15.15GHz on an underdoped YBa2Cu3O7-δ (YBCO) single crystal with Tc = 87K. 
The comparison is presented in Fig.1 in which the real part and the imaginary part of the 
complex conductivity curves were fitted simultaneously to Eq. (18) and Eq. (19) with the 
 6 -1
normal-state conductivity measured in Ref. [4] to be σn = 1.25 × 10 (Ωm) . The 
parameters we obtain from the fit are: H (0) T dH (T)/ dT | 186T (corresponding to 
 c2 c c2 Tc
 o
ξ = 13.3 A ), the GL parameter  = 48.7, and the factor k= σn /σGL=0.62, where we take 
γ= 7.8 for optimally doped YBCO in Ref. [11]. Using those parameters, we obtain G’i = 
1.62×10-3 (corresponding to ’ = 0.177). Note that the real part and the imaginary part of 
the complex conductivity were fitted to Eq. (18) and Eq. (19) with using the same fitting 
parameters. 
Figure 1. Points are the real part and the imaginary part of the complex conductivity of an 
underdoped YBCO in Ref. [4] in zero magnetic field. The solid lines are the theoretical 
values calculated from Eq. (18) and Eq. (19) with fitting parameters (see text). 
4. CONCLUSION 
 Time dependent Ginzburg-Landau equations with thermal noise describing the thermal 
fluctuations is used to investigate the complex conductivity in HTSC in 3D at zero 
magnetic field in the presence of strong thermal fluctuations on the mesoscopic scale in 
linear response. We use the self-consistent Gaussian approximation to treat the nonlinear 
interaction term in TDGL. Therefore the analytically explicit expression for the complex 
conductivity including all Landau levels we obtain is valid for both above and below the 
mean-field transition temperature. The real part and imaginary part of the conductivity are 
in good qualitative and even quantitative agreement with experimental data on YBCO. 
158 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 
 REFERENCES 
1. A.Larkin and A.Varlamov, Theory of uctuations in superconductors, (Clarendon Press, 
 Oxford, 2005). 
2. H.Schmidt, Z.Phys. 216 (1968) 336. 
3. D.P.Li, B.Rosenstein and V.Vinokur, J. of Superconductivity and Novel Magnetism 19 (2006) 
 369. 
4. M. S. Grbic, M.Pozek, D. Paar, V.Hinkov, M.Raichle, D.Haug, B.Keimer, N.Barisic, and A. 
 Dulcic, Phys. Rev. B 83 144508 (2011). 
5. J. B. Ketterson and S. N. Song, Superconductivity (Cambridge University Press, Cambridge, 
 1999). 
6. B. Rosenstein and V. Zhuravlev, Phys. Rev. B 76 (2007) 014507. 
7. R. J.Troy and A. T. Dorsey, Phys. Rev. B 47 (1993) 2715. 
8. N. Kopnin, Vortices in Type-II Superconductors: Structure and Dynamics (Oxford University 
 Press, Oxford, 2001). 
9. B. D. Tinh, D. Li and B. Rosenstein, Phys. Rev. B 81 (2010) 224521. 
10. D. Li and B. Rosenstein, Phys. Rev. B 65 (2002) 220504(R). 
11. B. D. Tinh and B. Rosenstein, Phys. Rev. B 79 (2009) 024518. 
 ĐỘ DẪN ĐIỆN XOAY CHIỀU CỦA VẬT LIỆU SIÊU DẪN 
 NHIỆT ĐỘ CAO KHI KHÔNG CÓ TỪ TRƯỜNG NGOÀI 
 Tóm tắt: Chúng tôi sử dụng phương trình Ginzburg-Landau phụ thuộc thời gian có kể 
 đến thăng giáng nhiệt để tính toán độ dẫn điện xoay chiều của vật liệu siêu dẫn nhiệt độ 
 cao trong mô hình ba chiều khi không có từ trường ngoài. Số hạng tương tác trong 
 phương trình được tuyến tính hóa bằng phương pháp gần đúng Gaussian và chúng tôi 
 tính đóng góp của các mức Landau cao hơn vào độ dẫn điện. Chúng tôi thu được biểu 
 thức giải tích chính xác độ dẫn điện xoay chiều bao gồm tất cả các mức Landau, biểu 
 thức này áp dụng cho nhiệt độ trên và dưới nhiệt độ tới hạn Tc. Kết quả của chúng tôi phù 
 hợp tốt với số liệu thực nghiệm của vật liệu siêu dẫn nhiệt độ cao YBa2Cu3O7-5. 
 Từ khóa: Độ dẫn điện xoay chiều; Siêu dẫn nhiệt độ cao; Phương trình Ginzburg-
 Landau.