Temperature dependence of anharmonic exafs oscillation of crystalline silicon
The extended X-ray absorption fine structure
(EXAFS) has been developed into a powerful
technique and is widely used to determine many
structural parameters and dynamic properties of
materials [1]. However, the position of atoms is not
stationary, and their interatomic distance always
changes due to thermal vibrations that were
detected by Beni & Platzman [2]. They cause
anharmonic effects on crystal vibrations and smear
out the EXAFS oscillations. The anharmonicity of
the potential yields additional terms in the EXAFS
oscillation, so if ignoring these terms, can lead to
non-negligible errors in the structural parameters.
The use of the moments of the radial distribution
function (or cumulants) to investigate local disorder
of EXAFS spectra was introduced by Rehr [3] who
showed that the Debye-Waller (DW) factor of
EXAFS spectra has a natural cumulant expansion in
powers of the photoelectron wavenumber. The
connection between the DW factor and the EXAFS
cumulants was described in detail in the cumulant
expansion approach (ratio method) by Bunker [4].
The ratio method is particularly appealing because
it summarizes the relevant structural and dynamic
information that is easily obtained from the
experimental EXAFS spectra.

Trang 1

Trang 2

Trang 3

Trang 4
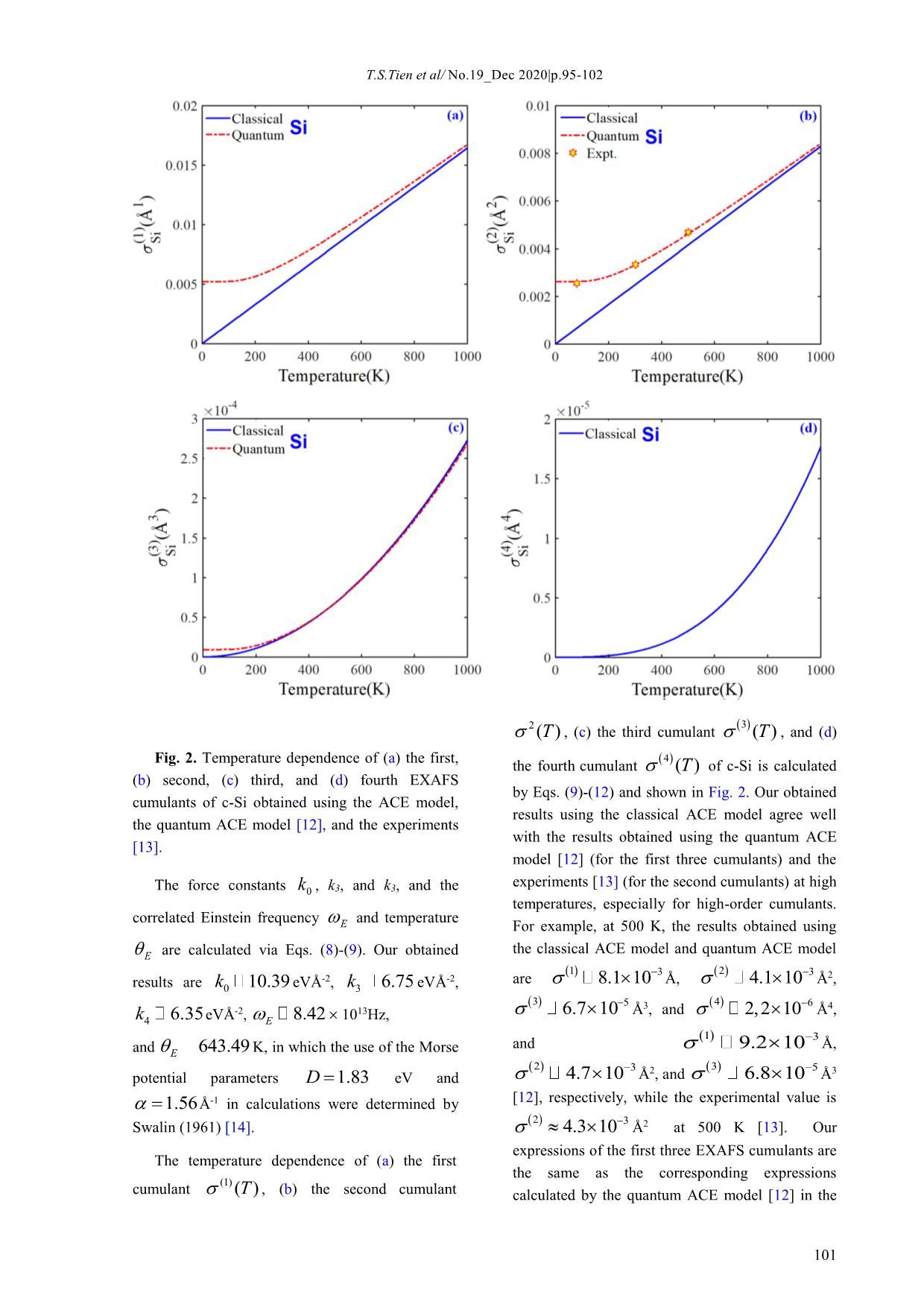
Trang 5
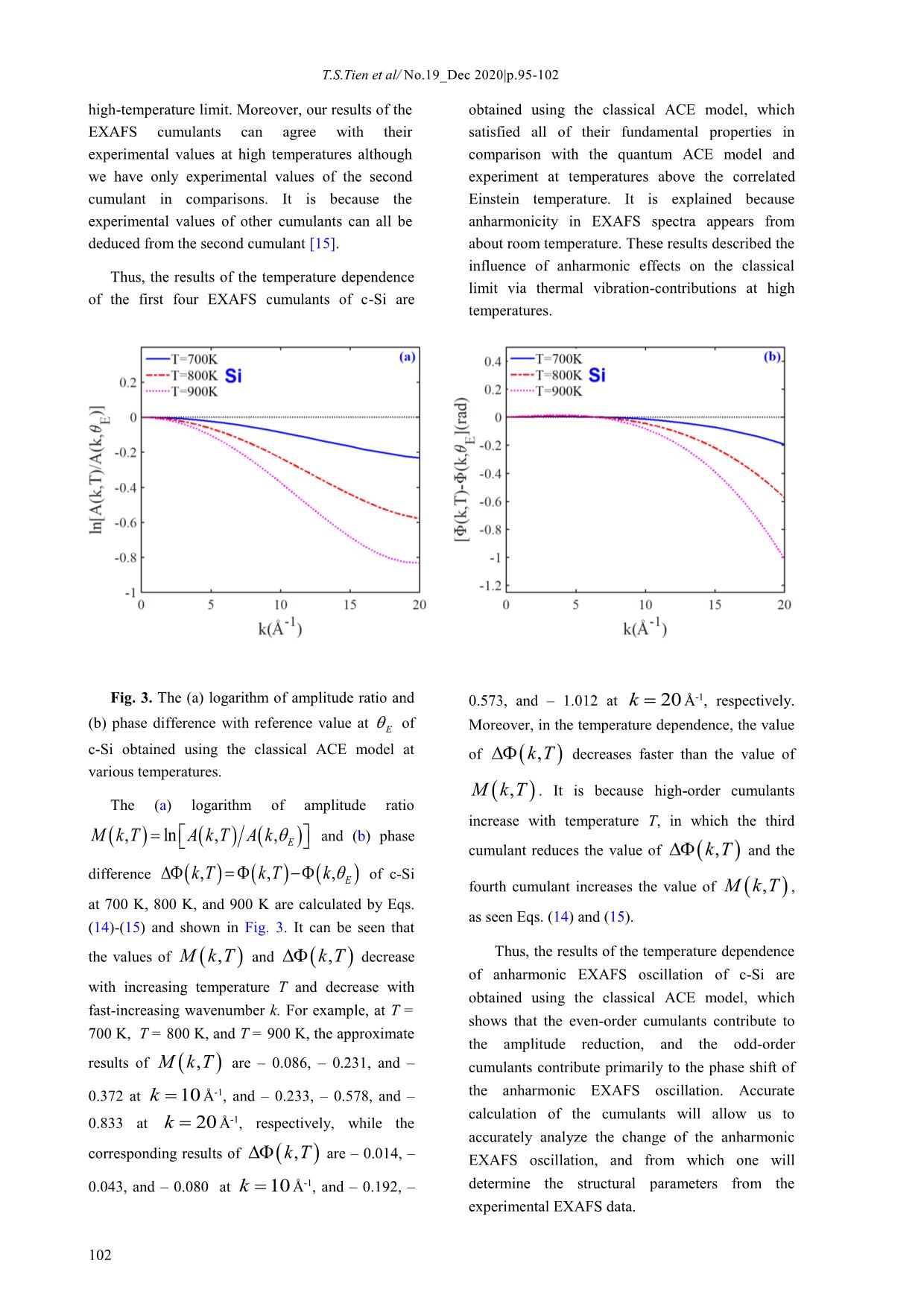
Trang 6

Trang 7

Trang 8
Tóm tắt nội dung tài liệu: Temperature dependence of anharmonic exafs oscillation of crystalline silicon

No.19_Sep 2020|Số 19 – Tháng 12 năm 2020|p.95-102 TẠP CHÍ KHOA HỌC ĐẠI HỌC TÂN TRÀO ISSN: 2354 - 1431 TEMPERATURE DEPENDENCE OF ANHARMONIC EXAFS OSCILLATION OF CRYSTALLINE SILICON Tong Sy Tien1,*, Le Viet Hoang2 1 Department of Basic Sciences, University of Fire, 243 Khuat Duy Tien, Thanh Xuan, Hanoi, Vietnam 2 Department of Physics, Hanoi University of Science, 334 Nguyen Trai, Thanh Xuan, Hanoi, Vietnam * E-mail: tongsytien@yahoo.com Article info Abstract: In this work, the anharmonic extended X-ray absorption fine structure Recieved: (EXAFS) oscillation of crystalline silicon (c-Si) is presented in terms of the Debye-Waller factor using the cumulant expansion approach up to the fourth- 16/9/2020 order. The first four EXAFS cumulant has been calculated based on the Accepted: classical anharmonic correlated Einstein (ACE) model and suitable analysis 10/12/2020 procedure, in which thermodynamic parameters are derived from the anharmonic effective potential obtained using the first shell near-neighbor contribution approach. The analysis of the temperature dependence of the EXAFS oscillation is performed via evaluating the influence of the cumulants Keywords: on the amplitude reduction and the phase shift of the anharmonic EXAFS EXAFS analysis; Debye- oscillation. The numerical results are found to be in good agreement with those Waller factor; Anharmonic obtained using the quantum ACE model and experiments at various correlated Einstein model; temperatures. The obtained results are useful in analyzing the experimental Crystalline silicon. EXAFS data of c-Si. 1. Introduction non-negligible errors in the structural parameters. The use of the moments of the radial distribution The extended X-ray absorption fine structure function (or cumulants) to investigate local disorder (EXAFS) has been developed into a powerful of EXAFS spectra was introduced by Rehr [3] who technique and is widely used to determine many showed that the Debye-Waller (DW) factor of structural parameters and dynamic properties of EXAFS spectra has a natural cumulant expansion in materials [1]. However, the position of atoms is not powers of the photoelectron wavenumber. The stationary, and their interatomic distance always connection between the DW factor and the EXAFS changes due to thermal vibrations that were cumulants was described in detail in the cumulant detected by Beni & Platzman [2]. They cause expansion approach (ratio method) by Bunker [4]. anharmonic effects on crystal vibrations and smear The ratio method is particularly appealing because out the EXAFS oscillations. The anharmonicity of it summarizes the relevant structural and dynamic the potential yields additional terms in the EXAFS oscillation, so if ignoring these terms, can lead to 97 T.S.Tien et al/ No.19_Dec 2020|p.95-102 information that is easily obtained from the 2. Basic formulae of EXAFS function and experimental EXAFS spectra. anharmonic effective potential of c-Si Recently, a classical anharmonic correlated 2.1. Basic formulae of EXAFS function Einstein (ACE) model [5] was developed based on The EXAFS oscillation for a single coordination the anharmonic effective (AE) potential [6] and the shell, including thermal disorders has the form: classical statistical theory [7]. This model has the advantage that the expressions of the first four k, T A k , T sin ( k , T ) , (1) EXAFS cumulants are obtained in explicit and simple forms, so it is very convenient for where A k, T and (,)kT are the EXAFS anharmonic EXAFS data analysis in the range of amplitude and phase, respectively, and k is the temperatures not too low. It has also been photoelectron wavenumber, and T is the successfully applied to investigate the anharmonic temperature. EXAFS oscillation for diamond crystals by Tien et al. [8]. However, the temperature dependence of The K-edge EXAFS oscillation for the distribution anharmonic EXAFS amplitude and phase has not of identical atoms is described within the framework been discussed in detail. Besides, it has been of single-scattering and plane-wave approximations. applied to successfully investigate crystalline Following the approach proposed by Tien [9], the germanium but has not yet been investigated logarithm of amplitude ratio and the linear crystalline silicon (c-Si). Therefore, the analysis of M k, T1 , T 2 ln A k , T 2 A k , T 1 the temperature dependence of anharmonic EXAFS phase difference k,,,, T T k T k T oscillation for c-Si will be a necessary addition to 1 2 2 1 evaluate the effectiveness of the classical ACE between temperatures T2 and T1 in the cumulant model in the EXAFS technique. expansion approach up to the fourth-order, which are given as follows: 4 2 2 2 2k 44 M k, T1 , T 2 2 k T 2 T 1 T 2 T 1 , (2) 3 3 1 1 1 ... k3 and k4 are local force constants giving asymmetry of 2.2. Thermodynamic parameters and potential due to the inclusion of anharmonicity. anharmonic effective potential of c-Si The Morse potential is assumed to describe the To determine the thermodynamic parameters of interatomic interaction model for the potential a system, it is necessary to specify its AE potential energy of a diatomic molecule. Applying the Morse and force constants [10]. One considers a potential to calculate the interaction energy between monatomic system with an anharmonic effective each pair of atoms in cubic metals was proposed by potential (ignored the constant contribution) is Girifalco and Weizer [11]. In the present study, we extended up to the fourth-order: expand the Morse potential to the fourth-order: 1 V(), x k x2 k x 3 k x 4 (4) eff 2 0 3 4 98 T.S.Tien et al/ No.19_Dec 2020|p.95-102 7 VxDe( ) 2 xx 2 e DDxDx 2 2 3 3 Dx 4 4 . (5) 12 where x is the same previously defined value, backscattering (B) atoms, including correlation describes the width of the potential, and D is the effects and taking into account only the nearest- dissociation energy. neighbor interactions, the AE potential [6] is given by In the relative vibrations of absorbing (A) and ˆˆ Veff V(), x V xR AB R ij (6) i A,, B j A B Mi vector, the sum i is the over absorbers ( iA ) and where MMMMABAB/ is the reduced mass of the absorber and backscatterer backscatterers ( iB ), and the sum j is over the nearest neighbors. with masses MA and MB, respectively, Rˆ is a unit Fig. 1. Structural model of c-Si. Applying Eqs. (5) and (6) to the structure of c- Comparing Eq. (4) with Eq. (7), we deduce the Si with a mass of atoms is MAB M m, as seen local force constants , k3, and k4 as follows: in Fig. 1, the AE potential is written as 7 35 1519 k D 2,,. k D 3 k D 4 7 35 1519 03 3 36 4 2592 V() x D 2 x 2 D 3 x 3 4 x 4 . eff 3 36 2592 (8) (7) The thermal vibration of atoms is characterized by the correlated Einstein frequency E and The local force constants k0 , k3, and k4 are temperature , which are calculated from the deduced from Eq. (7) as follows: E effective force constant k0 in the following forms: k eff 10DDhE h 10 EE , , (9) m kBB k m where k is the Boltzmann constant, is the B kk03, , and k4 are expressed in terms of the Morse reduced Planck constant. potential parameters via Eqs. (8) and (9). Consequently, the correlated Einstein frequency E and temperature E , and force constants 99 T.S.Tien et al/ No.19_Dec 2020|p.95-102 3. Temperature dependence of EXAFS The analysis of the EXAFS spectra usually uses the oscillation within the classical ACE model first four EXAFS cumulants [10]. The expressions of the first four cumulants of diamond crystals The EXAFS cumulants are explicitly related to within the classical ACE model are given as low-order moments of the distribution function. follows [8]: 1 15k 5 2 ; B T , (10) 28D 4 (2)32kkBB 2 22TT , (11) 7Dm E 2 2 3 45kB 225 ; 23T , (12) 98D 2 3 2 3 4 687kB 32229 ; 24T . (13) 686D 18 Substituting the anharmonic EXAFS cumulants from Eqs. (10)-(13) into Eqs. (2) and (3) to calculated the logarithm of amplitude ratio M k,, T12 T and the linear phase difference k,, T12 T , the results are obtained as 3 6kkBB2 229 4 3 3 M k,,, T1 T 2 2 k T 2 T 1 3 4 k T 2 T 1 (14) 7DD 343 2 15kBBB 12 k 11 30 k 3 2 2 kTT,,1 2 kTT 2 1 2 kTT 2 1 2 3 kTT 2 1 . (15) 14D 7 D r0 49 D Thus, the EXAFS cumulants using the CACE (9) in Sec. 2 and Eqs. (10)-(15) in Sec. 3 to the model can be expressed in the explicit and simple numerical calculations. Firstly, we perform forms of the mean-square relative displacement numerical calculations for the force constants of the (MSRD) 2 or temperature T . Consequently, the AE potential, the thermodynamic parameters, and logarithm of amplitude ratio and the phase the temperature dependence of the first four difference of the EXAFS oscillation is also EXAFS cumulants in the range from 0 K to 1000 expressed in simple forms of temperature via the K. Our results of the cumulants are compared with EXAFS cumulants. These obtained results can those obtained using the quantum ACE model [6] describe the influence of anharmonic effects on the in the range from 0 K to 1000 K by Hung et al. [12] classical limit at high temperatures, and show that and experiment at 80 K, 300 K, and 500 K by the cumulants are very useful for the quantitative Benfatto et al. [13]. Then, we analyze the logarithm treatment of the anharmonic EXAFS oscillation. of amplitude ratio and the phase difference of the anharmonic EXAFS oscillation with reference 4. Numerical results and discussions -1 value at E in the wavenumber range from 0 Å to To discuss the effectiveness of the classical 20 Å-1 at 700 K, 800 K, and 900K. Lastly, we ACE model for the analysis of the EXAFS evaluate and comment on the results obtained using oscillation of c-Si in this work, we apply Eqs. (8)- the classical ACE model in this work. 100 T.S.Tien et al/ No.19_Dec 2020|p.95-102 2 3 ()T , (c) the third cumulant ()T , and (d) Fig. 2. Temperature dependence of (a) the first, 4 the fourth cumulant ()T of c-Si is calculated (b) second, (c) third, and (d) fourth EXAFS by Eqs. (9)-(12) and shown in Fig. 2. Our obtained cumulants of c-Si obtained using the ACE model, results using the classical ACE model agree well the quantum ACE model [12], and the experiments with the results obtained using the quantum ACE [13]. model [12] (for the first three cumulants) and the experiments [13] (for the second cumulants) at high The force constants k0 , k3, and k3, and the temperatures, especially for high-order cumulants. correlated Einstein frequency and temperature E For example, at 500 K, the results obtained using E are calculated via Eqs. (8)-(9). Our obtained the classical ACE model and quantum ACE model 1 3 2 3 -2 -2 are 8.1 10 Å, 4.1 10 Å2, results are k0 10.39 eVÅ , k3 6.75 eVÅ , 3 5 3 4 6 4 -2 13 6.7 10 Å , and 2,2 10 Å , k4 6.35eVÅ , E 8.42 10 Hz, 1 3 and 9.2 10 Å, and E 643.49 K, in which the use of the Morse 2 3 2 3 5 3 potential parameters D 1.83 eV and 4.7 10 Å , and 6.8 10 Å 1.56Å-1 in calculations were determined by [12], respectively, while the experimental value is 2 3 Swalin (1961) [14]. 4.3 10 Å2 at 500 K [13]. Our expressions of the first three EXAFS cumulants are The temperature dependence of (a) the first the same as the corresponding expressions (1) cumulant ()T , (b) the second cumulant calculated by the quantum ACE model [12] in the 101 T.S.Tien et al/ No.19_Dec 2020|p.95-102 high-temperature limit. Moreover, our results of the obtained using the classical ACE model, which EXAFS cumulants can agree with their satisfied all of their fundamental properties in experimental values at high temperatures although comparison with the quantum ACE model and we have only experimental values of the second experiment at temperatures above the correlated cumulant in comparisons. It is because the Einstein temperature. It is explained because experimental values of other cumulants can all be anharmonicity in EXAFS spectra appears from deduced from the second cumulant [15]. about room temperature. These results described the influence of anharmonic effects on the classical Thus, the results of the temperature dependence limit via thermal vibration-contributions at high of the first four EXAFS cumulants of c-Si are temperatures. Fig. 3. The (a) logarithm of amplitude ratio and 0.573, and – 1.012 at Å-1, respectively. (b) phase difference with reference value at E of Moreover, in the temperature dependence, the value c-Si obtained using the classical ACE model at of decreases faster than the value of various temperatures. . It is because high-order cumulants The (a) logarithm of amplitude ratio increase with temperature T, in which the third M k, T ln A k , T A k ,E and (b) phase cumulant reduces the value of and the difference k,,, T k T k of c-Si E fourth cumulant increases the value of , at 700 K, 800 K, and 900 K are calculated by Eqs. as seen Eqs. (14) and (15). (14)-(15) and shown in Fig. 3. It can be seen that the values of M k, T and kT, decrease Thus, the results of the temperature dependence of anharmonic EXAFS oscillation of c-Si are with increasing temperature T and decrease with obtained using the classical ACE model, which fast-increasing wavenumber k. For example, at T = shows that the even-order cumulants contribute to 700 K, T = 800 K, and T = 900 K, the approximate the amplitude reduction, and the odd-order results of M k, T are – 0.086, – 0.231, and – cumulants contribute primarily to the phase shift of 0.372 at k 10 Å-1, and – 0.233, – 0.578, and – the anharmonic EXAFS oscillation. Accurate calculation of the cumulants will allow us to 0.833 at k 20 Å-1, respectively, while the accurately analyze the change of the anharmonic corresponding results of kT, are – 0.014, – EXAFS oscillation, and from which one will 0.043, and – 0.080 at Å-1, and – 0.192, – determine the structural parameters from the experimental EXAFS data. 102 T.S.Tien et al/ No.19_Dec 2020|p.95-102 5 Conclusions [5] N.V. Hung, T.S. Tien, N.B. Duc, D.Q. Vuong, High-order expanded XAFS Debye-Waller In this work, the classical ACE model has been factors of HCP crystals based on classical used successfully in the analysis of the anharmonic anharmonic correlated Einstein model, Mod. Phys. EXAFS oscillation of c-Si. The EXAFS analysis is Lett. B 28 (21) (2014) 1450174. performed based on evaluating the contribution of terms of the Debye-Waller factor in the cumulant [6] N.V. Hung and J.J. Rehr, Anharmonic expansion approach up to the fourth-order. The correlated Einstein-model Debye-Waller factors, Phys. Rev. B 56 (1) (1997) 43-46. results of the first four EXAFS cumulants are not only expressed in explicit and simple forms of the [7] E.A. Stern, P. Livins, Z. Zhang, Thermal temperature T or MSRD but also satisfy all of their vibration and melting from a local perspective, fundamental properties in temperature dependence. Phys. Rev. B 43 (11) (1991) 8850-8860. The analytical results show the role and meaning of [8] T.S. Tien, N.V. Hung, N.T. Tuan, N.V. the EXAFS cumulants for the amplitude reduction Nam, N.Q. An, N.T.M. Thuy, V.T.K. Lien, N.V. and the phase shift of the anharmonic EXAFS Nghia, High-order EXAFS cumulants of diamond oscillation. The obtained results are very useful for crystals based on a classical anharmonic correlated analyzing the experimental data of the anharmonic Einstein model, J. Phys. Chem. Solids 134 (2019) EXAFS oscillation of c-Si. 307-312. The good agreement of our numerical results with [9] T.S Tien, Advances in studies of the those obtained using the quantum ACD model and the temperature dependence of the EXAFS amplitude experiments at various temperatures show the and phase of FCC crystals, J. Phys. D: Appl. Phys. 53 (2020) 315303. effectiveness of the classical ACE model for calculating and analyzing the anharmonic EXAFS [10] T. Yokoyama, K. Kobayashi, T. Ohta, A. oscillation of c-Si. The obtained results can be applied Ugawa, Anharmonic interatomic potentials of to the analysis of the anharmonic EXAFS oscillation diatomic and linear triatomic molecules studied by of c-Si starting from about the correlated Einstein extended x-ray-absorption fine structure, Phys. temperature to just before the melting point. Rev. B 53 (10) (1996) 6111-6122. Acknowledgments [11] L.A. Girifalco and V.G. Weizer, Application of the Morse potential function to cubic The authors are thankful to Professor Nguyen metals, Phys. Rev. 114 (3) (1959) 687-690. Ba Duc for helpful discussions and comments. [12] V.V. Hung and H.K. Hieu, Study the REFERENCES Temperature Dependence of EXAFS Cumulants of Si and Ge by the Anharmonic Correlated Einstein [1] F.W. Lytle, D.E. Sayers, E.A. Stern, Model, Commun. Phys. 21 (1) (2011) 25-34. Extended x-ray-absorption fine-structure technique. [13] M. Benfatto, C.R. Natoli, A. Filipponi, II. Experimental practice and selected results, Phys. Thermal and structural damping of the multiple- Rev. B 11 (1975) 4825-4835. scattering contributions to the x-ray-absorption coefficient, Phys. Rev. B 40 (14) (1989), 9626- [2] G. Beni and P.M. Platzman, Temperature 9635. and polarization dependence of extended x-ray absorption fine-structure spectra, Phys. Rev. B 14 [14] R.A.Swalin, Theoretical calculations of (4) (1976) 1514-1518. the enthalpies and entropies of diffusion and vacancy formation in semiconductors, J. Phys. [3] J.J. Rehr and R.C. Albers, Theoretical Chem. Solids 18 (4) (1961) 290-296. approaches to x-ray absorption fine structure, Rev. [15] N.V. Hung, C.S. Thang, N.B. Duc, D.Q. Mod. Phys. 72 (3) (2000) 621-654. Vuong, T.S. Tien, Temperature dependence of [4] G. Bunker, Applications of the ratio theoretical and experimental Debye-Waller factors, thermal expansion and XAFS of metallic Zinc, method of EXAFS analysis to disordered systems, Physica B 521 (2017)198-203. Nucl. Instrum. Methods 207 (1983) 437-444. 103 T.S.Tien et al/ No.19_Dec 2020|p.95-102 SỰ PHỤ THUỘC VÀO NHIỆT ĐỘ CỦA DAO ĐỘNG EXAFS PHÍ ĐIỀU HÒA CỦA TINH THỂ SILIC Tống Sỹ Tiến, Lê Việt Hoàng Thông tin bài viết Tóm tắt Trong công việc này, dao động của phổ cấu trúc tinh tế mở rộng (EXAFS) phi Ngày nhận bài: điều hòa của tinh thể silic đã được biểu diễn qua các số hạng của hệ số Debye- 16/9/2020 Waller bằng phương pháp khai triển cumulant đến bậc bốn. Bốn EXAFS Ngày duyệt đăng: cumulant đầu tiên đã được tính toán dựa trên mô hình Einstein tương quan phi 10/12/2020 điều hòa (ACE) cổ điển và qui trình phân tích phù hợp, trong đó các tham số nhiệt động được rút ra từ hàm thế hiệu dụng phi điều hòa thu được bằng cách Từ khóa: tíếp cận các đóng góp lân cận của lớp nguyên tử đầu tiên. Việc phân tích sự Phân tích EXAFS; Hệ số phụ thuộc vào nhiệt độ của dao động EXAFS được thực hiện thông qua việc Debye-Waller; Mô hình đánh giá ảnh hưởng của các cumulant vào sự giảm biên độ và sự dịch pha. Các Einstein tương quan phi kết quả tính số được tìm thấy trùng hợp tốt với các kết quả thu được bằng mô điều hòa; Tinh thể silic. hình ACE lượng tử và thực nghiệm ở các nhiệt độ khác nhau. Các kết quả thu được là rất hữu ích đối trong việc phân tích các dữ liệu EXAFS thực nghiệm của c-Si. 104
File đính kèm:
 temperature_dependence_of_anharmonic_exafs_oscillation_of_cr.pdf
temperature_dependence_of_anharmonic_exafs_oscillation_of_cr.pdf

