Tài liệu Ôn tập vật lý 2 - Điện trường
I. ĐIỆN TÍCH
- Điện tích trong một hệ kín là bảo toàn.
- Điện tích của vật chất gồm điện tích âm và điện tích dương. Điện tích âm có nguồn
gốc từ các electron, điện tích dương là do các proton nguyên tử. Điện tích của 1 electron là –
e (e = 1,6.10-19C ), điện tích của 1 proton la +e. Điện tích của vath bao giờ cũng là bội số của
e – Điện tích của vật chất bị lượng tử hóa.
* Mật độ điện tích :
1. Mật độ điện dài λ
- Một vật có mật độ điện dài λ, nghĩa là trên 1 đơn vị chiều dài của vật, điện tích là λ.
- Khái niệm mật độ điện tích dài thường dùng trong trường hợp vật có hình dạng mảnh,
sợi
Vd: Một vòng dây kim loại mảnh bán kính R, điện tích phân bố đều, có tổng điện tích
là Q. Mật độ điện tích dài của vòng dây trên là :
Trong trường hợp tổng quát là hàm phụ thuộc theo biến chiều dài , . Lúc này
điện tích toàn phần của vật được tính:
Tích phân theo chiều dài
Vd: Một thanh mảnh AB dài L được tích điện, biết mật độ đien tích dài trên thanh được
phân bố theo hàm tuyến tính, tăng dần theo chiều từ A→B. Biết mật độ điện tích dài tại A, B
lần lượt là . Tính điện tích toàn phần thanh AB?

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
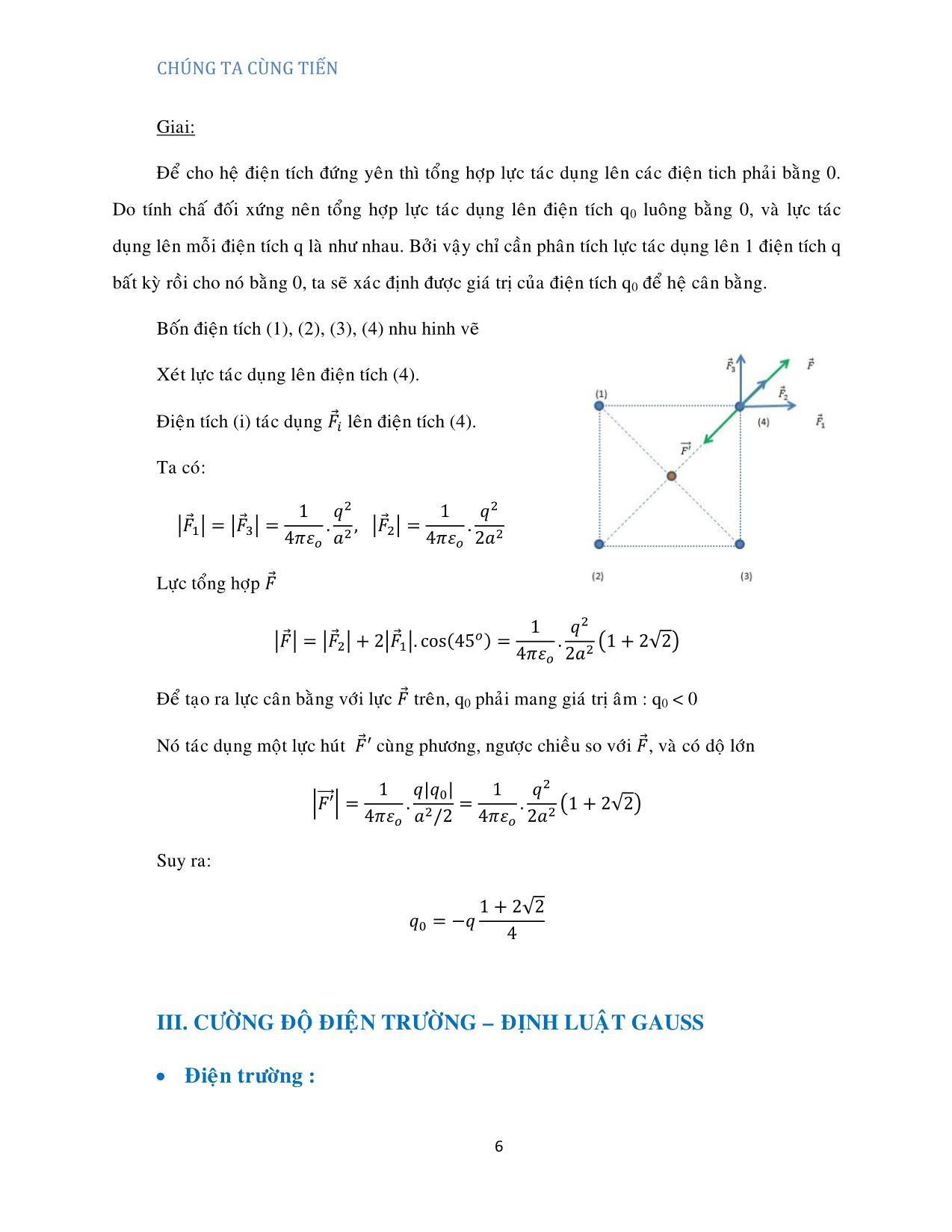
Trang 6

Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Tài liệu Ôn tập vật lý 2 - Điện trường

CHÚNG TA CÙNG TIẾN
ĐIỆN TRƯỜNG
Gồm 6 phần: 1. Điện tích
2. Định luật Coulomb
3. Cường độ Điện trường – Định luật Gauss
4. Công của điện trường – Điện thế
5. Liên hệ giữa điện trường và điện thế
6. Vật dẫn trong điện trường
7. Tụ điện
8. Năng lượng điện trường.
- Tài liệu do các CTV chương trình Chúng Ta Cùng Tiến thực hiện
- Tài liệu được biên soạn dựa trên kiến thức được học, tìm hiểu cũng như kinh
nghiệm của các CTV, bởi vậy không thể tránh khỏi thiếu sót, bới vậy các bạn hãy
coi đây như một tài liệu tham khảo, giúp các bạn trong quá trình học tập cũng như
chuẩn bị cho kỳ thi sắp tới
- Mọi ý kiến đóng góp phản hồi xin gửi về
Fanpage: https://www.facebook.com/Chungtacungtien/
Group – online: https://www.facebook.com/groups/chungtacungtien.hcmut/
- Bản quyền thuộc về Cộng đồng Chúng Ta Cùng Tiến
1
CHÚNG TA CÙNG TIẾN
I. ĐIỆN TÍCH
- Điện tích trong một hệ kín là bảo toàn.
- Điện tích của vật chất gồm điện tích âm và điện tích dương. Điện tích âm có nguồn
gốc từ các electron, điện tích dương là do các proton nguyên tử. Điện tích của 1 electron là –
e (e = 1,6.10-19C ), điện tích của 1 proton la +e. Điện tích của vath bao giờ cũng là bội số của
e – Điện tích của vật chất bị lượng tử hóa.
* Mật độ điện tích :
1. Mật độ điện dài λ
- Một vật có mật độ điện dài λ, nghĩa là trên 1 đơn vị chiều dài của vật, điện tích là λ.
- Khái niệm mật độ điện tích dài thường dùng trong trường hợp vật có hình dạng mảnh,
sợi
Vd: Một vòng dây kim loại mảnh bán kính R, điện tích phân bố đều, có tổng điện tích
là Q. Mật độ điện tích dài của vòng dây trên là :
Trong trường hợp tổng quát là hàm phụ thuộc theo biến chiều dài , . Lúc này
điện tích toàn phần của vật được tính:
∫
Tích phân theo chiều dài
Vd: Một thanh mảnh AB dài L được tích điện, biết mật độ đienä tích dài trên thanh được
phân bố theo hàm tuyến tính, tăng dần theo chiều từ A→B. Biết mật độ điện tích dài tại A, B
lần lượt là . Tính điện tích toàn phần thanh AB?
2
CHÚNG TA CÙNG TIẾN
Giai:
Chọn gốc , chiều trục Ox hướng theo từ A→B. Mật độ điện tích trên thanh tăng
dần theo tọa độ x. Mật độ điện tích dài tại điểm coa tọa độ x là:
, do mật độ điện tích tăng theo hàm tuyến tính ‼‼
Vậy điện tích toàn phân trên thanh là:
∫ ∫ ∫ ( )
2. Mật độ điện tích mặt
- Một vật có mật độ điện mặt , nghĩa là trên 1 đơn vị diện tích của vật, điện tích là .
- Khái niệm mật độ điện mặt dùng với các vật có phân bố điện tích trên bề mặt. Vd:
bản phẳng rộng, quả cầu rỗng.
Vd: Một quả cầu rỗng bán kính R, phân bố điện tích đều, tổng điện tích phân bố trên
bề mặt là Q. Mật độ điện tích mặt của quả cầu trên là:
Trong trường hợp tổng quát là hàm phụ thuộc theo biến diện tích, . Lúc này
điện tích toàn phần của vật được tính:
∫
Tích phân theo diện tích.
Một trường hợp chúng ta rát hay gặp đó là vat có dạng đĩa tròn. Trong trường hợp mật
độ điện tích mặt đĩa phụ thuộc vào bán kính r, tính từ tâm đĩa: . Lúc này
, biến tích phân lúc này là r. Biểu thức tính điên tích toàn phần của vât là:
∫
3
CHÚNG TA CÙNG TIẾN
Vd: Một đĩa tròn bán kính R. Có mật độ điện tích mặt phân bố theo bán kính r, tính từ
tâm đĩa: ( ). Biết điện tích toàn phần của đĩa là . Xác định , theo các
biến đã biết?
Giải:
Theo công thức trên, khi biết được hàm mật độ điện mặt theo bán kính r. Ta tính được
điện tích toàn phần của đĩa (=Q)
∫ ∫ ( )
Suy ra:
3. Mật độ điện tích khối
- Một vật có mật độ điện khối , nghĩa là trên 1 đơn vị thể tích của vật, điện tích là .
- Khái niệm mật độ điện khối được dùng với hầu hết các vật có kích thước (khối).
Vd: Một quả cầu đặc bán kính R, phân bố điện tích đều theo đơn vị thể tích. Qủa cầu
có điện tích toàn phần Q. Mật độ điện tích khối là :
Trong trường hợp tổng quát là hàm phụ thuộc theo biến thể tích, . Lúc này
điện tích toàn phần của vật được tính:
∫
Tích phân theo thể tích.
4
CHÚNG TA CÙNG TIẾN
Một trường hợp chúng ta rất hay gặp đó là vật có dạng cầu. Trong trường hợp mật độ
điện tích khối của quả cầu phụ thuộc vào bán kính r, tính từ tâm : . Lúc này
, biến tích phân lúc này là r. Biểu thức tính điên tích toàn phần của vât là:
∫
Vd: Một quả cầu đặc bán kính R, mật độ điện tích khối phân bố theo bán kính r, tính từ
tâm quả cầu:
( )
{
Tính điện tích toàn phần của qua ... ng:
- Điện tích điểm, quả cầu (rỗng, đặc) tích điện: MẶT CẦU
- Sợi dây dài tích điện, ống trụ tích điện : MẶT TRỤ (KÍN)
- Mặt phẳng rộng, đĩa dày rộng: KHỐI TRỤ ĐỨNG.
Bước 3: Ap dụng định luạt Gauss, tính cường độ điện trường E:
∫ ⃗ ⃗
Gỉa sử ta chọn được mặt Gauss thỏa mãn: Điện trường tại các điểm trên mặt Gauss
bằng nhau và vector cường độ điện trường ⃗ cùng phướng với vector pháp tuyến ⃗ .
Biểu thức xác định cường độ điện trường E lúc này trở thành:
∫ ⃗ ⃗ ∫
Với
- E là độ lớn cường độ điện trường xác định tại mặt Gauss (lưu ý: điện
trường tại các điểm nằm trên mặt Gauss cĩ độ lớn như nhau).
- S diện tích mặt Gauss
- là điện tích “chứa” trong mặt Gauss.
Ta bắt đầu với một ví dụ đơn giản:
Vd: Xác định cường đơ điện trường gây ra bởi 1 điện tích điểm q, cách điện tích một
khoảng là r?
Giai:
Bước 1: - Vật của chúng ta là điện tich điểm
- Đường sức điện của điện tich điểm
10
CHÚNG TA CÙNG TIẾN
Bước 2: Điện tích điểm → Mặt Gauss: MẶT CẦU
Cần xác định cường độ điện trường tại điểm cách điên tích q một khoảng là r. Vậy
chọn mặt Gauss là mặt cầu tâm là vị trí đặt điện tích điểm, bán kính r.
Bước 3: Ap dụng định luạt Gauss
∫ ⃗ ⃗ ∫
Với:
- E = E( r ) là cường độ điện trường tại điểm cách điên tích q một
khoảng r
- là diện tích mặt Gauss (là diện tích mặt cầu bán kính r )
- là điện tích “chứa” trong mặt Gauss
Vậy:
Kết quả nhận trên đúng với kiến thức cũ ta đã biết ‼ ^^
Tiếp đến với một ví dụ khác:
Vd: Một quả cầu đăc bán kính R, tích điện với mật độ điện tích khối:
( )
Xác định cường độ điện trường tại vị trí (tính từ tâm quả cầu):
i. r ≤ R
ii. r > R
Giải:
i. Xác định cường độ điện trường E( r) tại điểm cách tâm quả cầu một khoảng r ≤ R.
Chọn mặt Gauss là mặt cầu đồng tâm quả cầu, bán kính r ≤ R (?????)
Theo công thức Gauss, ta sẽ có:
11
CHÚNG TA CÙNG TIẾN
Tiếp theo cần xác định là bao nhiêu???? Với , nhắc lại, là điện tích chứa
trong mặt Gauss, tức là mặt cầu đồng tâm quả cầu, bán kính r ≤ R. Nói cách khác
là phần điện tích của quả cầu đông tâm bán kính r ≤ R
Tính ?? Coi lại mục I. ĐIỆN TÍCH, phần mật độ điện tích khối ‼!
Với r ≤ R
∫ ( ) ( )
Vậy:
( )
ii. Xác định cường độ điện trường E( r) tại điểm cách tâm quả cầu một khoảng r > R.
Ta có:
Mặt Gauss của chúng ta trong trường hợp này là mặt cầu đồng tâm quả cầu, bán kính r
> R. Bới vậy là điện tích toàn phần của quả cầu ( do r > R, nên quả cầu nằm hoàn toàn
trong mặt Gauss).
∫ ( )
Vậy:
12
CHÚNG TA CÙNG TIẾN
Trong giới hạn chương trình học, đề thi cuối kỳ. Các bạn sẽ tính được hầu hết các bài
toán liên quan đến xác định cường độ điện trường bằng cách áp dụng định luật Gauss như đã
trình bày ơ trên ‼!
Tuy nhiên khi thi, các bạn nên nhớ công thức xác định cường độ điện trường của một số
hệ điện tich cơ bản, điều này giúp các bạn tiết kiệm thời gian hơn. Chúng ta có thể ra một số
công thức sau:
1. Qủa cầu đặc bán kính R, mật độ điện tích khối đều .
{
Nếu cho điện tích toàn phần Q thì:
{
2. Sợi dây dài vô hạn, mật độ điện dài λ.
λ
3. Ông trụ rỗng, dài, bán kính R, mật độ điện dài λ
{ λ
4. Mặt phẳng rộng vô hạn, mật độ điện tích mặt
13
CHÚNG TA CÙNG TIẾN
LƯU Ý: Trong các công thức, kết qua trinh bày ở trên, mặc định hằng số điện môi
tương đối của vật đang xét bằng 1. Khi gặp bài toán liên quan tới hằng số điện môi
, các bạn cần bổ chính vào kết quả ‼!
IV. CÔNG CỦA ĐIỆN TRƯỜNG – ĐIỆN THẾ
1. Đặc điểm của cơng của điện trường
Giống như lực hấp dẫn, lực của điện trường là lực thế, tức là công của nó thực hiện
được không phụ thuộc hình dạng đường đi mà chỉ phụ thuộc điểm đầu điểm cuối
2. Điên thế
- Điên thế của một điểm trong điện trường đo bằng công để đưa một đơn vị điện tích từ
điểm đó ra xa vô cùng
- Điện thê là một đại lượng vô hướng
- Điện thế giảm dọc theo chiều đường sức
Điện thế tại một điểm cách điểm tích một đoạn có giá trị là :
Muốn tính điện thế tại một điểm trong điện trường của một vật tích điện có hình
dạng bất lỳ, ta chia vật đó thành nhiều phần vô cùng nhỏ rồi tính điện thế tại điểm
đó do từng phần nhỏ đó gây ra, sau đó tổng lại (hoặc thực hiện các phép lấy tổng,
tích phân. Tham khảo dạng toán này trong tập tài liệu của thầy Châu nha! Mấy
dạng bài sử dụng tích phân tính, trong đó trình bày kỹ lắm!
3. Chồng chập điện thế
14
CHÚNG TA CÙNG TIẾN
Điện thế tại một điểm trong điện trường do nhiều điện tích gây ra bằng tổng điện thế
do từng điện tích gây ra riêng rẽ tại điểm đó
∑
LƯU Ý: Chồng chập điện thế là phép cộng ĐẠI SỐ, còn chồng chập điện trường là
phép cộng VECTOR
4. Thế năng tính điện
Một điện tích có thế năng tĩnh điện trong điện trường. Nếu một điện tích dược đưa
từ xa vô cùng về một điểm có điện thê V thì mất một công là . Gía trị này được gọi
là thế năng tĩnh điện của tại điểm đó. Thế năng
Trong điện trường của điện tích điểm , thế năng tĩnh điện của điện tích là :
Thế năng tính điện của hệ gồm :
- n = 2:
- n = 3:
Thế năng tính điện cũng tuân theo định luật bảo toàn năng lượng. Nếu một hệ gồm
nhiều điện tích tương tác với nhau thì năng lượng toàn phần của hệ được bảo toàn,
tức là:
15
CHÚNG TA CÙNG TIẾN
Trong đó, K là động năng toàn phần của hệ, U là thế năng tĩnh điện của hệ
Vd: Cho n hạt thủy ngân hình cầu được tích điện đến mức mỗi giọt có điện thế V0.
Tính điện thế của giọt thủy ngân do n giọt trê hợp thành?
Giai:
Gọi bán kính mỗi giọt nhỏ là r
Điện tích mỗi giọt là
Điện tích của giọt sau khi nhập là :
(điện tích hệ kín bảo toàn)
Và điện thế trên mặt giọt lớn là:
Với R là bán kính giọt lớn
Thể tích n giot nhỏ và thể tích giọt lớn sau khi nhập bằng nhau‼, nên
√
Vậy:
√
√
Vd: Tính công để đặt các điện tích +Q, +Q và –Q từ xa vô cùng vào 3 đỉnh của một tam
giác đều cạnh a?
Giải:
Công để sắp đặt các điện tích bằng thế năng tĩnh điện toàn phần của hệ sau khi các
điện tích nằm ở đỉnh tam giác, tức là:
16
CHÚNG TA CÙNG TIẾN
Vd: Một electron được thả không vận tốc đầu từ một khoảng cách r0 = 0.2 nm tới một
proton đứng yên. Tìm động năng của electron kho nó cách proton r = 0.1 nm
Giải:
Do khối lượng lớn hơn rất nhiều so với electron nên proton có thể xem là đứng yên.
Năng lượng ban đầu: Chỉ có thê năng tĩnh điện
Năng lượng lúc sau: Gồm thế năng tĩnh điện và động năng electron K
Bảo toàn năng lượng:
( )
V. LIÊN HỆ GIỮA ĐIỆN TRƯỜNG VÀ ĐIỆN THẾ
Biểu thức liên hệ giữa vector cường độ điện trường ⃗ là điện thế V
⃗
Toán tử gradien (grad) là toán tử “tác dụng” lên một hàm hướng, “kết quả” là một hàm
hữu hướng. Công thức khai triển cụ thể biểu thức trên phụ thuộc vào hệ tọa độ ta chọn
Hệ Descartes : V=V(x,y,z)
⃗ ( ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗ )
Với ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗ ⃗ là các vector đơn vị ứng với ba trục Ox, Oy, Oz
17
CHÚNG TA CÙNG TIẾN
Vd: Trong không gian tồn tại điện thê : . Tính ⃗
Giải:
Ta có:
⃗ ( ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗ ) ( ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗ )
⃗ ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗
Hệ tọa độ trụ:
⃗ ( ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗ )
Với ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗ ⃗ là các vector đơn vị trong hệ tọa độ trụ.
Nếu: : – Trường hợp này thường gặp, thì :
⃗ ⃗⃗⃗ ⃗⃗⃗
Vd: Tính điện thế gây ra bởi sợi dây dài vô hạn, mật độ điện dài λ ?
Giải:
Điện trường tạo bởi sợi dây dài vô hạn, mật độ điện dài λ
⃗ ⃗ ⃗⃗⃗ ⃗⃗⃗
Vậy, điện thế gây ra bởi sợi dây :
Hệ tọa độ trụ:
⃗ ( ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗⃗ )
Với ⃗⃗⃗ ⃗⃗⃗⃗ ⃗⃗⃗ ⃗⃗ là các vector đơn vị trong hệ tọa độ trụ.
18
CHÚNG TA CÙNG TIẾN
Nếu: : – Trường hợp này thường gặp, thì :
⃗ ⃗⃗⃗ ⃗⃗⃗
Vd: Điện thế của điện tích là:
Điện trường gây ra bởi điện tích điểm :
⃗
⃗⃗⃗ ⃗⃗⃗ ⃗⃗⃗
HIỆU ĐIỆN THẾ
Gỉa thiết điện trường trong khơng gian chỉ phụ thuộc khoảng cách, tức là ⃗ ⃗
Xét 2 điểm M, N nằm trong khơng gian trên. Hiệu điện thế giữa 2 điểm M, N:
Ta cĩ: ⃗ ⃗ . Lúc này:
⃗ ⃗⃗⃗ ⃗⃗⃗
Về độ lớn:
∫ ∫ ∫
Vd: Hai mặt trụ đồng trục dài vơ hạn tích điện đều bằng nhau và trái dấu cĩ bán kính lần
lượt là R và 3R. Hiệu điện thế giữa chúng la U. Mật độ điện dài λ trên mỗi trụ bằng?
Giải:
Xét khơng gian nằm giữa 2 mặt trụ (R ≤ r ≤ 3R)
Cường độ điện trường trong khơng gian này là :
19
CHÚNG TA CÙNG TIẾN
Hiệu điện thế giữa hai mặt trụ:
∫ ∫
Vậy:
Vd: Cho một quả cầu tích điện đều với mật độ điện tích khối , bán kính . Hiệu điện thế
giữa hai điểm cách tâm và là?
Giải:
Để xác định được hiệu điện thế giữa hai điểm cách tâm và , ta cần biết cường độ điện
trường giữa hai điểm ấy, tức là | Trong khơng gian này:
Hiệu điện thế giữa hai điểm cách tâm (A) và (B):
∫ ∫
Vd: Cho hai mặt phẳng kim loại rộng A, B song song, tích điện đều và cách nhau một
đoạn d. Lần lượt cĩ mật độ điện mặt ( . Giua chúng là chất điện mơi
cĩ hằng số điện mơi . Hiệu điện thê U giữa hai mặt?
Giải:
Coi 2 bản kim loại A, B như những mặt phẳng rộng
vơ hạn tích điện mặt đều. Điện trường tạo ra bởi 2 bản là
điện trường đều.
Xét trong khơng gian nằm giữa 2 bản A, B.
Điện trường ⃗⃗⃗⃗ gây ra bởi bản A, cĩ độ lớn:
20
CHÚNG TA CÙNG TIẾN
Chiều hướng sang phải ( do >0→ >0), như hình vẽ
Tương tự ta cĩ điện trường ⃗⃗⃗⃗ gây ra bơi bản B, cĩ độ lớn:
Chiều hướng sang trái, nhu hình vẽ.
Do , nên điện trường tổng hợp cĩ hướng theo hướng của ⃗⃗⃗⃗ . Điện
trường tổng hợp này cĩ độ lớn:
Điện trường này là điện trường đều, nên hiệu điện thế giữa hai bản là :
VI. VẬT DẪN TRONG ĐIỆN TRƯỜNG
1. Tính chất của vật dẫn cân bằng tĩnh điện
- Điện tích chỉ tập trung ở mặt ngồi mặt dẫn
- Điện trường tại mặt vật dẫn phải cĩ phương vuơng gĩc với mặt vật dẫn tại mỗi điểm của
nĩ
- Vật dẫn cân bằng tĩnh điện là một vật đẳng thế
2. Vật dẫn đặt trong điện trường
* Hiện tượng điện hưởng :
Đặt một vật dẫn trung hịa ở gần một vật mang điện khác. Dưới tác dụng của điện trường
do vật mang điện gây ra, trong vật dẫn các điện tích trái dấu với điện tích vật mang điện sẽ
chuyển động về đầu vật dẫn, gần vật mang điện. Các điện tích cùng dấu chuyển động về đầu cịn
lại, xa vật mang điện. Vật dẫn trung hịa bây giờ tích điện trái dấu ở hai đầu của nĩ.
21
CHÚNG TA CÙNG TIẾN
Hiện tượng vật dẫn trung hịa trở thành tích điện do ảnh hưởng của vật mang điện, gọi là
hiện tượng điện hưởng. Điên hưởng cĩ 2 trường hợp: Điện hưởng một phần và điện hưởng tồn
phần
Khi làm đề, nếu nhắc đến vật dẫn thì phải tính đến trường hợp xảy ra hiện tượng điện
hưởng. Mà nếu đề khơng nĩi gì thì tự hiểu là điện hưởng tồn phần! – giờ tìm hiêu điên hưởng
tồn phần thơi :v
Đĩ là trường hợp vật dẫn trung hịa A bao bọc hồn tồn vật mang điện C. Khi đĩ nếu vật
màn điện cĩ điện tích +q thì mặt trong A của vật dẫn bao bọc sẽ xuất hiện điện tích –q, mặt
ngoài vật dẫn sẽ có điện tích +q.
Vd: Một hệ các quả cầu đồng tâm, dẫn điện gồm:
- 1 điện tích điểm Q đặt tại tâm
- 1 quả cầu rỗng, bán kính trong R, bán kính ngoài 2R. Tích điện Q0
Xác định cường độ điện trường tại:
i. r < R
ii. R < r < 2R
iii. r > 2R
Giải:
Ap dụng định luật Gauss
i. r < R: Mặt Gauss là mặt cầu đông tâm bán kính r < R
Trong trường hợp này:
ii. R < r < 2R: Mặt Gauss là mặt cầu đông tâm bán kính R < r < 2R
22
CHÚNG TA CÙNG TIẾN
Điện tích chứa trong vật dẫn nên xay ra điên hưởng (toàn phần), mặt trong cầu rỗng sẽ
có điện tích là –Q.
Lúc này: , gồm điện tích điểm và điện tích của mặt trong cầu rỗng
Vậy:
Kết quả này đúng với tính chất của vật dẫn cân bằng đó là điện trường bên trong vật
dẫn bằng 0
iii. r > 2R: Mặt Gauss là mặt cầu đông tâm bán kính r > 2R
Vật dẫn ban đầu có điện tích Q0, do hiện tưởng cộng hưởng, mặt trong quả cầu rỗng có
điện tích –Q, mặt ngoài quả cầu sẽ có điện tích là Q+Q0. Lúc này:
Vậy :
VII. TỤ ĐIỆN
1. Tụ điện
Công thức liên hệ giữa điện dung C, điện tích Q và hiệu điện thế giữa hai bản tụ:
Có 3 dạng tụ điện chúng ta thường gặp: TỤ PHẲNG, TỤ CẦU, TỤ TRỤ
a. TỤ PHẲNG
23
CHÚNG TA CÙNG TIẾN
Cấu tạo bởi hai bản phẳng có điện tích S, đặt cách nhau một khoảng nhỏ d. Giua hai
bản đặt một lớp điên môi có điện dung
Điện dung của tụ phẳng:
b. TỤ CẦU
Tụ điện cầu là tụ điện được cấu tạo bởi hai cầu rỗng: 1 cầu bán kính R1, được bao bởi
cầu rỗng đồng tâm khác bán kính R2 (R2 > R1). Giua hai qua cầu, đặt một lớp điện môi có
điện dung
Điện dung của tụ cầu:
c. TỤ TRỤ
Tụ trụ gồm 2 ống trụ đông tâm cao L, bán kính R1, R2 ((R2 > R1). Giua hai ống trụ, đặt
một lớp điện môi có điện dung
Điện dung của tụ trụ:
( )
2. Năng lượng của tụ điện.
Tụ điện điện dung C, tích điện Q, đặt dưới hiệu điện thế U.
Năng lượng của tụ điện.
Hoặc:
24
CHÚNG TA CÙNG TIẾN
VIII. NĂNG LƯỢNG ĐIỆN TRƯỜNG
Ở đâu tồn tại điện trường, ở đó có năng lượng
Năng lượng điện trường E trong miền thế tích V
∫
Trong trường hợp cường độ điện trường có tính đối xứng cầu, tức là , thì
, biến tích phân lúc này là r. Biểu thức tính năng lượng lúc này trở thành.
∫ ( )
LƯU Ý: Khi găp bai toán liên quan tới tính năng lượng điện trường thì phải sử
dụng công thức tông quát trên
Vd: Qủa cầu bán kính R, tích điện Q phân bố đều trên toàn thể tích. Cho biết hằng số
điện môi ở trong và ngoài quả cầu đều bằng . Tính :
i. Năng lượng bên trong quả cầu
ii. Năng lượng bên ngoài quả cầu
iii. Năng lượng toàn phần quả cầu
Giải:
i. Điện trường bên trong quả cầu (r < R)
Năng lượng bên trong quả cầu:
∫ ( ) ∫
25
CHÚNG TA CÙNG TIẾN
ii. Điện trường bên ngồi quả cầu (r > R)
Năng lượng bên trong quả cầu:
∫ ( ) ∫
iii. Năng lượng tồn phần quả cầu
26
File đính kèm:
 tai_lieu_on_tap_vat_ly_2_dien_truong.pdf
tai_lieu_on_tap_vat_ly_2_dien_truong.pdf

