Supercontinuum generation in photonic crystal fibers infiltrated with liquids
In this paper we present the development of a new direction in so-called optofluidics,
namely the research of photonic crystal fibers (PCF) infiltrated with liquids. In particular we concentrate on the flagship application of PCF, the process of Supercontinuum Generation (SG), in
which injected monochromatic pulse may be dramatically broadened (spectrally), which creates a
coherent beam generation of high brightness comparable to that of monochromatic lasers. The supercontinuum is formed when a collection of nonlinear processes act together upon a pump beam
in order to cause severe spectral broadening of the original pump beam. Explanation of this process is based on numerical simulations for Generalized Nonlinear Schrodinger equation (GNLSE) ¨
which describes the rich nonlinear dynamics of pulse propagation in nonlinear dispersive media.
All nonlinear phenomena involved in SG will be analyzed. We present specially activity of the
Polish-Vietnamese Group from the beginning in 2016 to recent time in this domain. Some recent
scientific projects concerning fiber physics of our Group in the near future, especially applications
in Biology and Medicine will be mentioned.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
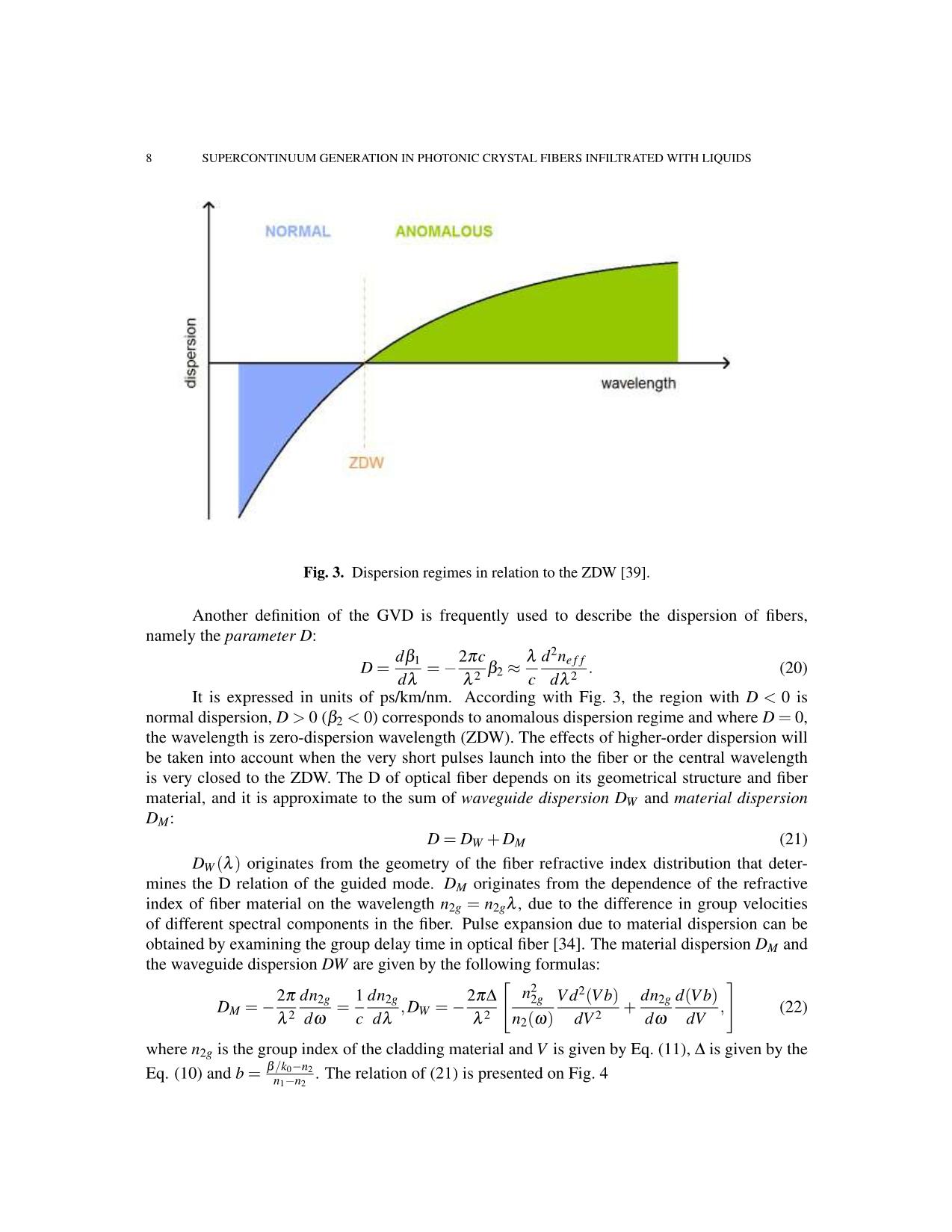
Trang 8
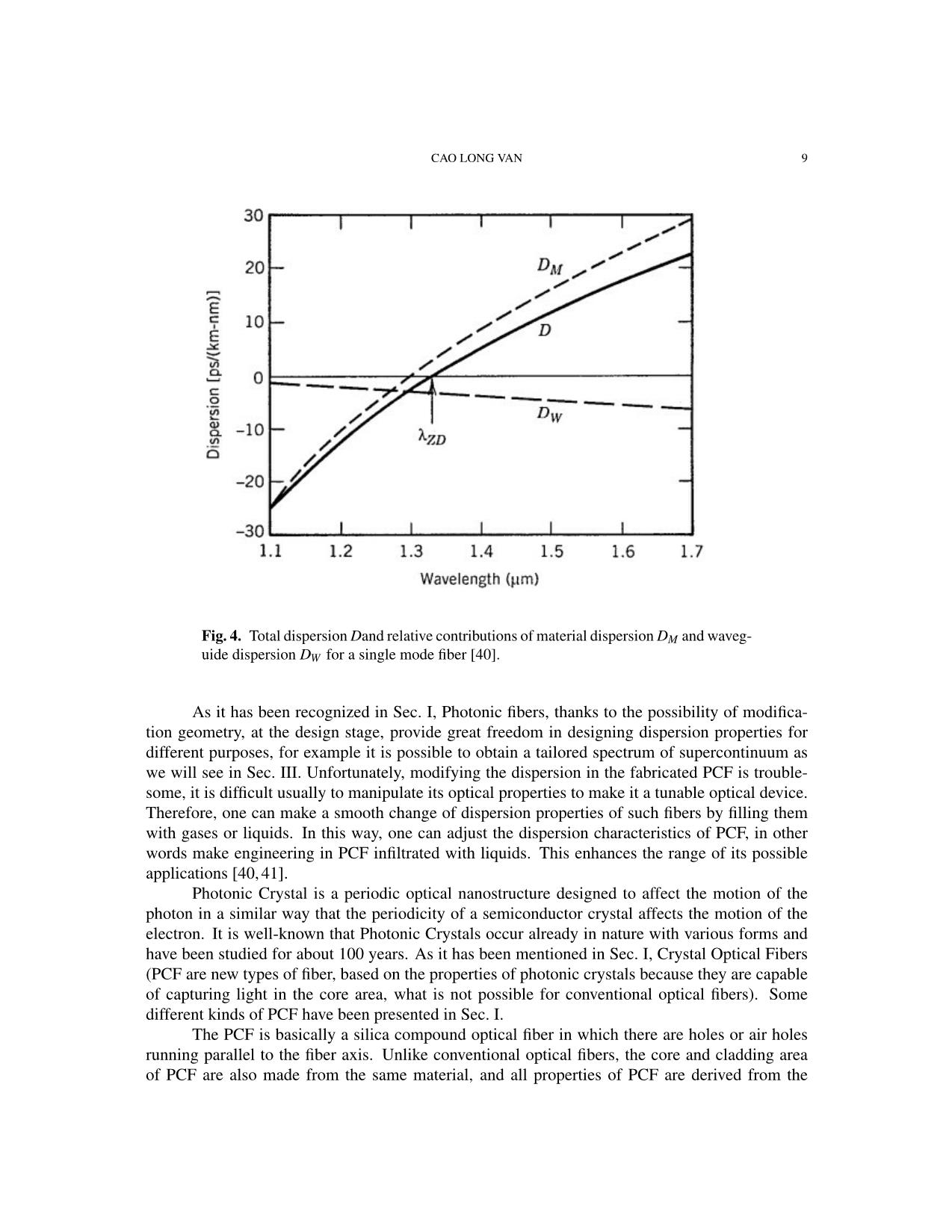
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Supercontinuum generation in photonic crystal fibers infiltrated with liquids

Communications in Physics, Vol.31, No. 1 (2021), pp. 1-22 DOI:10.15625/0868-3166/15547 REVIEW PAPER SUPERCONTINUUM GENERATION IN PHOTONIC CRYSTAL FIBERS INFILTRATED WITH LIQUIDS CAO LONG VAN† Institute of Physics, University of Zielona Gora,´ Prof. Szafrana 4a, 65-516 Zielona Gora,´ Poland †E-mail: caolongvanuz@gmail.com Received 28 September 2020 Accepted for publication 14 October 2020 Published 5 January 2021 Abstract. In this paper we present the development of a new direction in so-called optofluidics, namely the research of photonic crystal fibers (PCF) infiltrated with liquids. In particular we con- centrate on the flagship application of PCF, the process of Supercontinuum Generation (SG), in which injected monochromatic pulse may be dramatically broadened (spectrally), which creates a coherent beam generation of high brightness comparable to that of monochromatic lasers. The su- percontinuum is formed when a collection of nonlinear processes act together upon a pump beam in order to cause severe spectral broadening of the original pump beam. Explanation of this pro- cess is based on numerical simulations for Generalized Nonlinear Schrodinger¨ equation (GNLSE) which describes the rich nonlinear dynamics of pulse propagation in nonlinear dispersive media. All nonlinear phenomena involved in SG will be analyzed. We present specially activity of the Polish-Vietnamese Group from the beginning in 2016 to recent time in this domain. Some recent scientific projects concerning fiber physics of our Group in the near future, especially applications in Biology and Medicine will be mentioned. Keywords: Photonic Crystal Fiber, Supercontinuum Generation, Generalized Nonlinear Schrodinger¨ equation. Classification numbers: 42.55.Tv; 88.60.np; 42.25.-p. ©2021 Vietnam Academy of Science and Technology 2 SUPERCONTINUUM GENERATION IN PHOTONIC CRYSTAL FIBERS INFILTRATED WITH LIQUIDS I. INTRODUCTION Supercontinuum is a phenomenon based on a set of effects resulted from combined inter- action of linear and nonlinear properties of optical medium involved in photonic crystal fibers (PCFs). The input monochromatic pulse of light is broadened spectrally to form a continuous spectrum in a beam of high brightness, even comparable to that of a monochromatic laser. The output spectrum becomes much wider than the input (Fig. 1). Fig. 1. Supercontinuum generation. Discovery of the lasers realized experimentally by Maiman [1] for the first time in 1960 gives as a light source with very high intensity. This created a very important domain of physics, namely nonlinear optics [2]. To this time the majority of optical effects are considered only in the case of a linear material response of a medium to an incoming light field. However when the intense light field is high, nonlinear optical effects appear which dramatically modify properties of the incoming light. Experimental nonlinear optics started from the experiment on second harmonic generation performed in 1961 by Franken et al. [3]. In this experiment, two photons having the same frequency made up a photon of the doubled frequency by the nonlinear material responses of the medium. In this phenomenon, a light spectrum of an enormous broaden bandwidth was generated together with new frequency components, so one can say that a phenomenon, later called as Supercontinuum Generation (SG) has been observed there for the first time. The further development of nonlinear optics provided to the appearance of conventional optical fibers which made the revolution not only in nonlinear optics but also in higher technolo- gies as in telecommunication for last few decades. This discovery is treated as one of the greatest scientific advents in the XX century. A new field of physics appeared, namely nonlinear fiber optics [4]. This field had developed intensively, so new nonlinear phenomena were discovered, such as self-phase modulation in fibers [5] and parametric mixing processes [6, 7]. In particular optical solitons [8] and their dynamics [9, 10] have been highly interested by researchers. These CAO LONG VAN 3 nonlinear phenomena played an important role in explanation of SG mentioned above. Now we have an ultra-broad spectrum spanning almost the complete visible region of light [11, 12]. Guiding of light in optical fibers based on the phenomenon of total internal reflection (TIR). A break point in development of optical fibers has been made in the 1950s by covering of glass fiber with a material with a lower refractive index [13,14]. This type of fiber structure including the core and cladding is used as the basic solution until now. Since the first experimental realization of low-loss optical fiber in 1970 [15], worldwide telecommunication experienced extraordinary growth. However the conventional fiber guiding the light by TIR has several limits related to op- tical nonlinearities and attenuation. Several new guiding mec ... eering to achieve a flat dispersion characteris- tic necessary in SG. Secondly, the proposed PCF can also be tuned by means of temperature to modulate the dispersion characteristic. Finally, Carbon Tetrachloride has similar refractive index of fused silica that as a filling medium it can easily incorporated in all-fiber optical systems. The measured dispersion characteristics, wavelength-dependent losses and effective mode area obtained in the PCF described in [68] have been taken into account in GNLSE for considering SG. The temporal coherence of SG in the proposed PCF has been also calculated for the complex degree of first -order coherence according with the formula given in Ref. [70]. SG in this model was verified also experimentally. We concluded that the agreement between simulation and ex- periment is remarkably good. It certainly confirms the dominant role of single mode regime and all-normal dispersion features of observed SG dynamics. Two fibers selected in Ref. [53] have been analyzed with respect to SG. It follows that both proposed fibers are good candidates for all-fiber SC sources as alternative to glass core fibers, because nonlinearity of chloroform is higher than silica and its toxicity is negligible. Two chosen fibers allow for SG on the basis of two mechanisms. The first one is SC in all-normal dispersion regime, so can be coherent. The second one is soliton fission based SC in anomalous regime. CAO LONG VAN 19 In Ref. [59] some selected types of the suspended-core SCF infiltrated with water have been analyzed in the relation to SG. We have shown that in SCF made of borosilicate glass one can obtain flat dispersion characteristics which are required for efficient SG in fibers. We demonstrate in Ref. [54] experimentally SG in PCFs with CCl4-filled cores when it is pumped with 90-fs-long pulses with a central wavelength of 1560 nm. Here we have used shorter pulses than previously to suppress the noise and to increase the temporal of the recorded SC pulses [71, 72]. We also used different pump wavelengths to better match the dispersion char- acteristics and the location of ZDW. In this way as it has been emphasized above, optimal PCFs are chosen with good nonlinear properties, and at the same time, they are easy to incorporate in all-fiber systems. Furthemore we demonstrate for the first time that this SC can be achieved in hollow-core fibers with CCl4 infiltration and low-peak-power pulses. Evidently, the peak power of pump pulses used in this paper was 10 times smaller than that in our previous paper [52]. More- over, it is extremely low in comparison to that in Ref. [73], where peak power was MW level. We used shorter input pulses than those in previous papers, and therefore the effects of polarization and laser noise on coherence degradation were reduced. As it has been shown by numerical analysis, the considered fibers have the potential for high coherence. The results obtained in Ref. [54] prove that the use of CCl4-infiltrated PCFs is an interesting solution for compact all-fiber SG systems with low-power femtosecond lasers. We concluded also that a combination of low-cost, standard silica PCFs with cores infiltrated with CCl4 gives us possibility to develop efficient fibers with ultra-broadband transmission on short distances up to a few tens of cm. From the reason that the energy of the guided beams is confined in liquid cores, only a small fraction of light interacts with the silica walls in which it is highly attenuated. In consequence the work with liquid-core PCFs is challenging at the current stage, because it requires the use of dedicated reservoirs for input liquid. However, if silica fibers are used, all-fiber integrated systems are feasible to be constructed in the near future. All PCF samples used in experiments were fabricated in Institute of Electronic Materials Technology (ITME) in Warsaw. As we know, the use of these liquids as cores in photonic fibers made it possible to obtain a medium with strong light location in a medium with high non-linearity over long distances. Initially, research work was theoretical, but after mastering the methods of controlled liquid introduction into photonic fiber cores (hollow core), they were confirmed by experimental research. IV. CONCLUSIONS As it is has been presented above, development of nonlinear optics and optical fibers cre- ated the nonlinear optical fibers [4]. This leads to the new model of optical fibers using photonic crystal claddings i.e. the dielectric matter with periodic structure of refractive index. This new kind of fibers, called later as photonic crystal fibers (PCFs) with special optical properties possible to be tailored with high degree of freedom. Furthermore they can be adjusted to the needs of ex- periment. The appearance of PCF in the late 1990s is considered as a revolution comparable with the invention of laser before. PCFs overcome many limitations intrinsic to step index fibers and create an ideal platform for observing new optical phenomena, in particular so-called supercontin- uum generation (SG) which has reported for the first time in [74]. The big freedom in dispersion engineering of PCF allows SG to be performed optimally in the wide range of available pump sources, so one can use very short input pulses as well as high power continuous wave sources. 20 SUPERCONTINUUM GENERATION IN PHOTONIC CRYSTAL FIBERS INFILTRATED WITH LIQUIDS SG in PCF was immediately applied in many fields of science and technology. The freedom in dispersion tailoring is much more enhanced when PCF is filled by different liquids. Recent studies of SG concentrate on giving new insight into the spectral broadening mech- anism, adjusting supercontinuum properties to specific applications and creating new PCFs infil- trated by liquids suitable to SG through dispersion engineering of multicomponent glasses mate- rials. Our work belongs to this trend of study. A modern fiber optics laboratory has been created now in Vinh University. It can be used to carry out research in the field of non-linear fiber optics, fiber photonic systems and fiber optic sensors. We will design new kinds of PCFs, now infiltrated of new liquids and verify their optical properties, in particular their dispersion in this Laboratory. The first our paper with a complete experimental verification in our Laboratory has been already published [75]. ACKNOWLEDGEMENT I would like to express my deep gratitude to Dr. Le Van Hieu for his wonderful job editing my manuscript and making it suitable for Communications in Physics. REFERENCES [1] T. H. Maiman, Nature 187 (1960) 493–494. [2] J. A. Armstrong, N. Bloembergen, J. Ducuing and P. S. Pershan, Phys. Rev. 127, (1962) 1918–1939. [3] P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett. 7, (1961) 118–119. [4] G. P. Agrawal, Nonlinear fiber optics, fifth Edition, Elsever Academic Press (2013). [5] C. Lin and R. H. Stolen, Physical Review A 17 (1978) 1448. [6] R. H. Stolen, J. E. Bjorkholm and A. Ashkin, Appl. Phys. Lett. 24 (1974) 308. [7] R. Stolen, IEEE J. Quantum Electronics 11 (1975) 100. [8] J. M. Dudley, G. Genty, and S. Coen, Rev. Modern Phys. 78 (2006) 1135. [9] A. V. Husakou and J. Herrmann, Phys. Rev. Lett. 87 (2001) 203901. [10] J. P. Gordon, Opt. Lett. 11 (1986) 662. [11] J. M. Dudley and J. R. Taylor, Supercontinuum generation in optical fibers, Cambridge University Press, 2010. [12] R. R. Alfano, The Supercontinuum Laser Source, Springer, Berlin, 2006. [13] A. C. S. van Heel, Nature 173 (39), (1954). [14] H. H. Hopkins, N. S. Kapany, Nature 173 (39), (1954). [15] F. P. Kapron, D. B. Keck, R. D. Maurer, Appl. Phys. Lett. 17 (1970) 423. [16] S. John, Phys. Rev. Lett. 58 (1987) 2486. [17] E. Yablonovitch, Phys. Rev. Lett. 58 (1987) 2059. [18] E. Yablonovitch, T. J. Gmitter and K. M. Leung, Phys. Rev. Lett. 67 (1991) 2295. [19] C. Knight, T. A. Birks, P. St. J. Russell, D. M. Atkin, Opt. Lett. 21(19), (1996) 1547. [20] R. F. Cregan, B. J. Mangan, J. C. Knight, T. A. Birks, P. St. J. Russell, P. J. Roberts, D. C. Allan, Science 285 (1999) 1537. [21] A. D. Pryamikov, A. S. Biriukov, A. F. Kosolapov, V. G. Plotnichenko, S. L. Semjonov and E. M. Dianov, Opt. Express 19(2011) 1441. [22]S.F evrier,´ B. Beaudou and P. Viale, Opt. Express 18 (2010) 5142. [23] F. Couny, P. J. Roberts, T. A. Birks and F. Benabid, Opt. Express 16 (2008) 20626. [24] A. Argyros and J. Pla, Opt. Express 15 (2007) 7713. [25] Y. Y. Wang, N. V. Wheeler, F. Couny, P. J. Roberts and F. Benabid, Opt. Lett. 36 (2011) 669. [26] A. D. Pryamikov, A. S. Biriukov, A. F. Kosolapov, V. G. Plotnichenko, S. L. Semjonov and E. M. Dianov, Opt. Express 19 (2011) 1441. [27] NKT Photonics, LARGE MODE AREA PHOTONIC CRYSTAL FIBERS, https://www.nktphotonics.com/lasers-fibers/product/large-mode-area- photonic-crystal-fibers/ CAO LONG VAN 21 [28] A. Ortigosa-Blanch, J. C. Knight, W. J. Wadsworth, J. Arriaga, B. J. Mangan, T. A. Birks, P. St. J. Russell, Opt. Lett. 25 (2000) 1325. [29] A. S. Webb, F. Poletti, D. J. Richardson, J. K. Sahu, Opt. Eng. 46 (2007) 010503. [30] R. Buczynski, H. T. Bookey, D. Pysz, R. Stepien, I. Kujawa, J. E. McCarthy, A. J. Waddie, A. K. Kar and M. R. Taghizadeh, Laser Phys. Lett. 7 (2010) 666. [31] Y. Liu, Y. Wang, Z. Wang, X. Zhang, X.Liu, S. Gao, X. Wang and Pu Wang, Nanophotonics 7 (2018) 1307. [32] C. Wei, J. T. Young, C. R. Menyuk and J. Hu, OSA. Continuum. 2 (2019) 2123. [33] C. L. Van, Comm. Phys. 26 (2016) 301. [34] C. L. Van, Rev. Adv. Mater. Sci. 23 (2010) 8. [35] Y. R. Shen, Principles of nonlinear optics, Wiley, New York, 1984, Chap. 1. [36] M. Schubert and B. Wilhelmi, Nonlinear optics and quantum electronics, Wiley, New York, 1986, Chap. 1. [37] P. N. Butcher and D. N. Cotter, The elements of nonlinear optics, Cambridge University Press, Cambridge, UK, 1990, Chap. 2. [38] M. Ebnali-Heidari, Majid & Dehghan, F & Saghaei, Hamed & Koohi-Kamali, Farshid & Moravvej-Farshi, Mohammad, J. Modern Opt. 59 (2012) 1384-1390. [39] Le Van Hieu, PhD Thesis, University of Zielona Gora,´ 2018. [40] G. P. Agrawal, Fiber-optic communications systems, Third Edition, ISBNs: 0-471-21571-6 (Hardback); 0-471- 22114-7 (Electronic). [41] J. Pniewski, T. Stefaniuk, H. L. Van, V. C. Long, C. V. Lanh, R. Kasztelanic, G. Sepniewski,ˆ A. Ramaniuk, M. Trippenbach, R. Buczynski,˜ Applied Optics 55(19) (2016) 5033-5040. [42] J. C. Knight, Nature 424 (2003) 847-851. [43] C. M. Smith, N. Venkantaraman, M.T. Gallager, D. Mueller, J. A. West, N. F. Borreili, D. C. Allan and K. W. Koch, Nature 424 (2003) 657. [44] D. Pysz, I. Kujawa, R. Stepien, M. Klimczak, A. Filipkowski, M. Franczyk, L. Kociszewski, J. Buzniak, K. Harasny and R. Buczynski, Bull. Pol. Ac.: Tech. 62 (2014) 2300. [45] https://www.lumerical.com/products/mode/. [46] A. Fernando, E. Silvestre, P. Andres, J. J. Miret and M. V. Andres, Opt. Express 9 (2001) 687. [47] W. H. Reeves, J. C. Knight, P. St. J. Russell and P. J. Roberts, Opt. Express 10 (2002) 609. [48] K. Saitoh, M. Koshiba, T. Hasegawa and E. Sasaoka, Opt. Express 11 (2003) 843. [49] V. T. Hoang, R. Kasztelanic, A. Anuszkiewicz, G. Stepniewski,ˆ A. Filipkowski, S. Ertman, D. Pysz, T. Wolinski,˜ K. D. Xuan, M. Klimczak, R. Bucznski,˜ Optical Materials Express 8(11) (2018) 3568. [50] L. C. Van, V. T. Hoang, V. C. Long, K. Borzycki, K. D. Xuan, V. T. Quoc, M. Trippenbach, R. Bucznski,˜ J. Pniewski, Laser Phys. 30 (2020) 035105. [51] Q. H. Dinh, J. Pniewski, V. H. Le, A. Ramaniuk, V. C. Long, K. Borzycki, K. D. Xuan, M. Klimczak, R. Buczynski,˜ Applied Optics 57(15) (2018) 1. [52] V. T. Hoang, R. Kasztelanic, A. Filipkowski, G. Stepniewski,ˆ D. Pysz, M. Klimczak, S. Ertman, V. C. Long, T. R. Wolinski,˜ M. Trippenbach, K. D.Xuan, M. Smietana,´ R. Buczynski,˜ Opt. Mater. Express 9 (2019) 2264. [53] L. C. Van, V. T. Hoang, V. C. Long, K. Borzycki, K. D. Xuan, V. T. Quoc, M. Trippenbach, R. Bucznski˜ and J. Pniewski, Laser Physics 29(7) (2019) 1. [54] V. T. Hoang, R. Kasztelanic, G. Stepniewski,ˆ K. D. Xuan, V. C. Long, M. Trippenbach, M. Klimczak, R. Buczynski˜ and J. Pniewski, Appl. Opt. 59 (2020) 1559. [55] Q. H. Dinh, H. L. Van, K. D. Xuan, R. Kasztelanic, V. C. Long, Q. H. Quang, L. C. Van, L. M. Van, T. T. Doan and R. Bucznski,˜ dvances in Optics Photonics Spectroscopy & Applications IX, Publishing House for Science and Technology, 978-604-913-578-1 (2017). [56] K. D. Xuan, L. C. Van, V. C. Long, Q. H. Dinh, L. V. Xuan, M. Trippenbach, R. Bucznski,˜ Appl. Opt. 56 (2017) 1012. [57] A. S. Webb, F. Poletti, D. J. Richardson, J. K. Sahu, Opt. Eng. 46 (2007) 1. [58] I. Savelii, J. C. Jules, G. Gadret, B. Kibler, J. Fatome, M. E. Amraoui, N. Manikandan, X. Zheng, F. Des´ ev´ edavy,´ J. M. Dudley, J. Troles, L. Brilland, G. Renversez and F. Smektala, Opt. Mater. 33 (2011) 1661. [59] K. D. Xuan, L. C. Van, V. C. Long, Q. H. Dinh, L. V. Xuan, M. Trippenbach and R. Buczynski,˜ Appl. Opt. 56 (2017) 1012. 22 SUPERCONTINUUM GENERATION IN PHOTONIC CRYSTAL FIBERS INFILTRATED WITH LIQUIDS [60] V. H. Le, R. Buczynski,˜ V. C. Long, M. Trippenbach, K. Borzycki, A. N. Manh, R. Kasztelanic, Opt. Commun. 407 (2018) 417. [61] V. T. Hoang, B. Siwicki, M. Franczyk, G. Stepniewski,ˆ V. H. Le, V. C. Long, M. Klimczak, R. Bucznski,˜ Opt. Fiber Tech. 42 (2018) 119. [62] L. Shao, Z. Liu, J. Hu, D. Gunawardena and H.-Y. Tam, Micromachines 9 (2018) 145. [63] M. C. Gather and S. H. Yun, Nat. Photon. 5(7) (2011) 406. [64] X. Fan and S.-H. Yun, Nat. Methods. 11 (2014) 141. [65] V. T. Hoang, G. Stepniewski,ˆ K. H. Czarnecka, R. Kasztelanic, V. C. Long, K. D. Xuan, L. Shao, M. Smietana,´ R. Buczynski,˜ Appl. Sci. 9 (2019) 1. [66] Nguyen Viet Hung, Propagation of light pulses in dispersive nonlinear media, Master Thesis, Vinh University 9/2005 (in Vietnamese). [67] C. L. Van and P. P. Goldstein, University of Zielona Gora,´ 2008. [68] L. C. Van, A. Anuszkiewicz, A. Ramaniuk, R. Kasztelanic, K. D. Xuan, V.C. Long, M. Trippenbach, R. Buczynski,˜ J. Opt. 19 (2017) 125604. [69] L. C. Van, V. T. Hoang, V. C. Long, K. Borzycki, K. D. Xuan, V. T. Quoc, M. Trippenbach, R. Bucznski,˜ J. Pniewski,Laser Phys. 30 (2020) 035105. [70] J. M. Dudley, S. Coen, Opt. Lett. 27 (2002) 1180. [71] B. Gonzalo, R. D. Engelsholm, M. P. Sørensen and O. Bang, Sci. Rep. 8, (2018) 6579. [72] E. Genier, P. Bowen, T. Sylvestre, J. M. Dudley, P. Moselund and O. Bang, J. Opt. Soc. Am. B. 36 (2019) A161. [73] A. Bozolan, C. J. S. de Matos, C. M. B. Cordeiro, E. M. dos Santos and J. Travers, Opt. Express 16 (2008) 9671. [74] J. K. Ranka, R. S. Windeler, and A. J. Stentz Opt. Lett. 25 (2000) 796. [75] T. C. Le, T. V. Hoang, H. V. Le, D. Pysz, L. V. Cao, T. D. Bui, D. T. Nguyen, Q. D. Ho, M. Klimczak, R. Kasztelanic, J. Pniewski, R. Buczynski˜ and K. X. Dinh, Opt. Mater. Express 10 (2020) 1733.
File đính kèm:
 supercontinuum_generation_in_photonic_crystal_fibers_infiltr.pdf
supercontinuum_generation_in_photonic_crystal_fibers_infiltr.pdf

