Structure analysis of amorphous and liquid magnesium silicate
Magnesium silicate (Mg2SiO4) is one of the most abundant materials of the Earth’s upper mantle
[1, 2]. It is also an important component in many high technology applications [3]. Mg2SiO4 system has
been extensively investigated for a long time by both experiment (X-ray diffraction, nuclear magnetic
resonance, Raman spectroscopy technology) [4-6] and simulation (Molecular Dynamics, Monte Carlo)
[1-3, 7-11]. Knowledge of structure of Mg2SiO4 system in both solid and liquid states at different
temperature and pressure conditions is necessary for understanding about thermal change of the Earth
as well as application in the process of new material fabrication technology. The X-ray diffraction and
Neutron scattering experimental results showed that [8] Si atoms in Mg2SiO4 glass has mainly 4
coordinated oxygens and the mean bond length of Si-O is about 1.60 Å. Meanwhile the Mg atoms are
surrounded 5 oxygens and the Mg-O bond length is about 2.0 Å. Using nuclear magnetic resonance [4,
5] authors indicated that the coordination number of Mg is 5 and 6. The simulation results [2, 10, 11]
also showed that structure Mg2SiO4 comprise basic structural unit TOn (T= Si, Mg; n is the number of
oxygens that surrounded T atoms). There is change of the coordination number of Si and Mg atoms and
intermediate range order structure in magnesium silicate melts under compression [2]. Molecular
dynamics simulation of MgSiO3 liquid [12, 13] clarified structural organization, network topology as
well as the degree of polymerization under compression. In this work, we clarify structure of amorphous
Mg2SiO4 at 0 and 40 GPa and compared with the one of liquid Mg2SiO4. Especially, the origin of subpeaks in radial distribution function of O-O, Si-Si and Mg-Mg pairs also explain via analysis the TOn
units as well as the corner-, edge- and face-sharing bonds between adjacent structural units TOn.

Trang 1
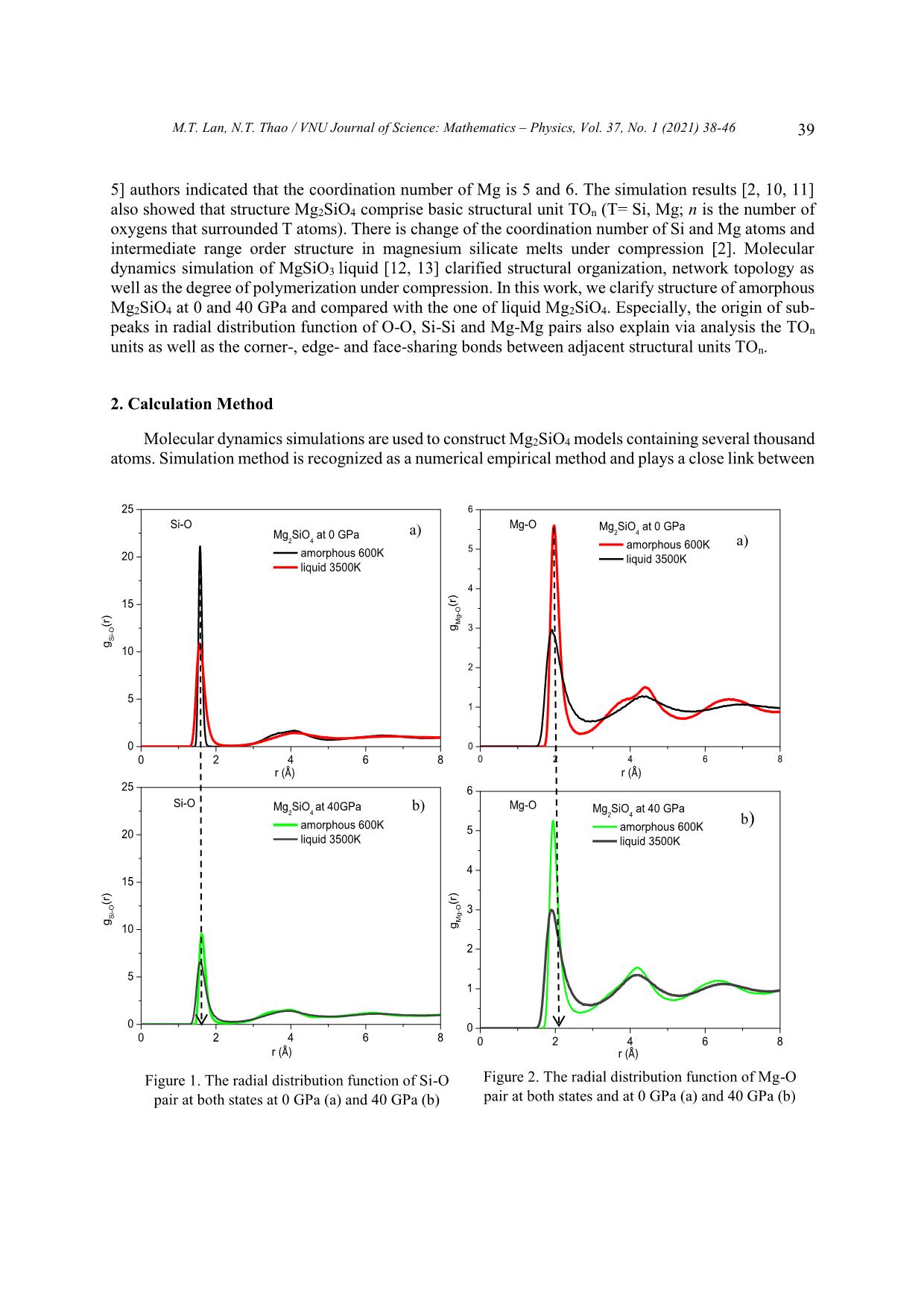
Trang 2
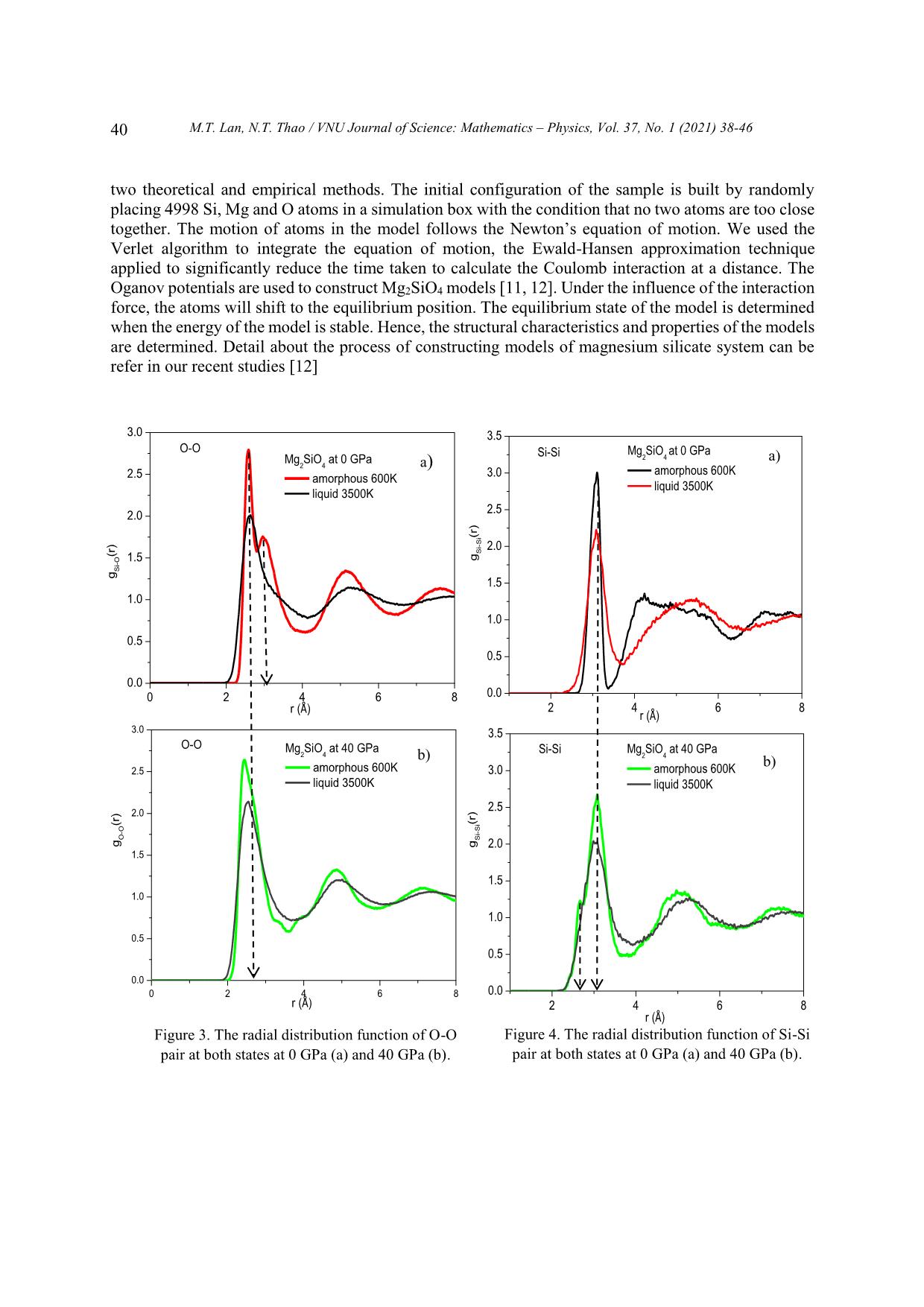
Trang 3
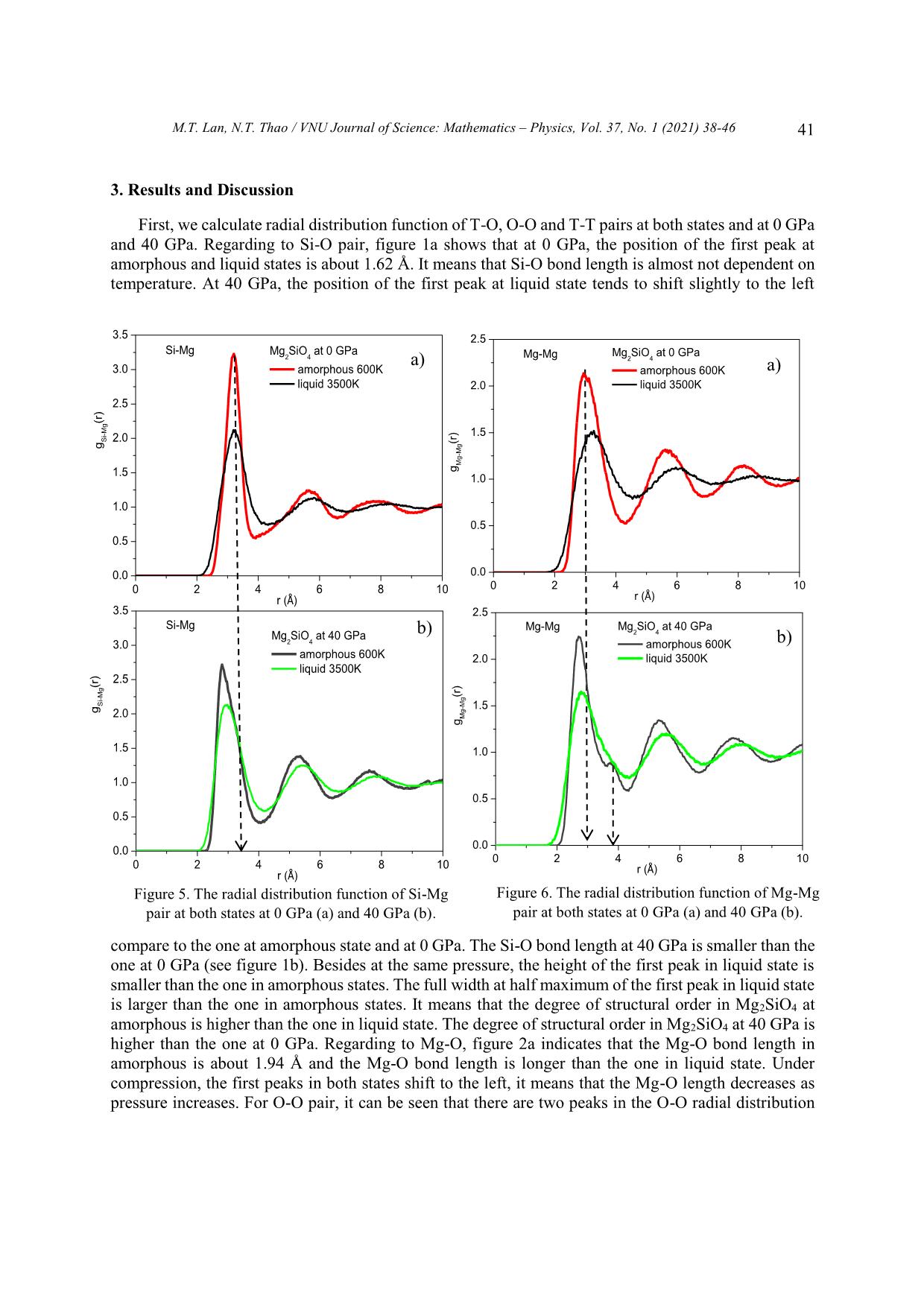
Trang 4

Trang 5

Trang 6
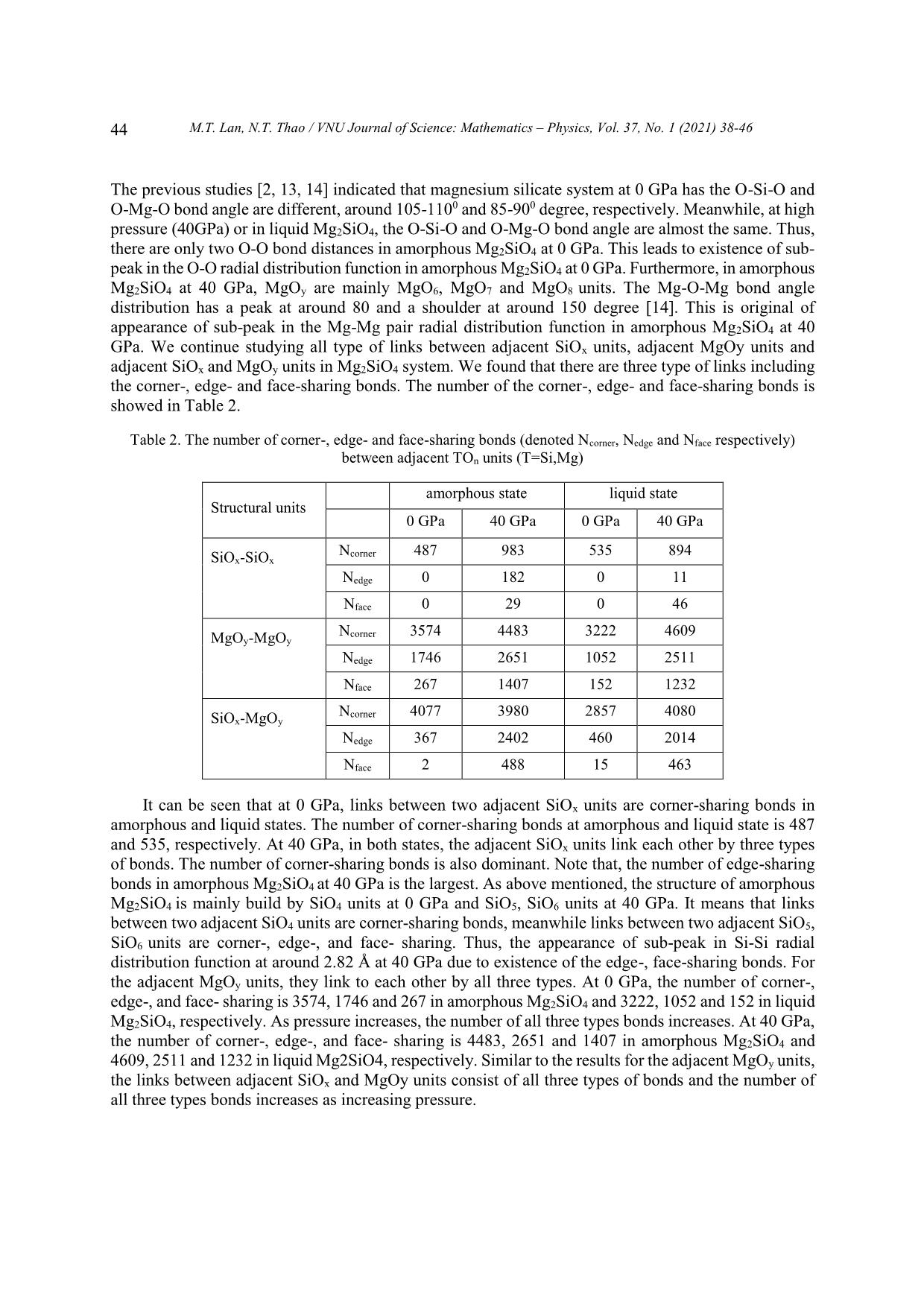
Trang 7

Trang 8

Trang 9
Tóm tắt nội dung tài liệu: Structure analysis of amorphous and liquid magnesium silicate

VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 Original Article Structure Analysis of Amorphous and Liquid Magnesium Silicate Mai Thi Lan1,*, Nguyen Thi Thao2 1Hanoi University of Science and Technology, 1 Dai Co Viet, Hai Ba Trung, Hanoi, Vietnam 2Hong Duc University, 565 Quang Trung, Dong Ve, Thanh Hoa, Vietnam Received 05 May 2020 Revised 19 May 2020; Accepted 15 June 2020 Abstract: We use the Oganov potentials and period boundary condition to perform molecular dynamics simulation of amorphous and liquid Mg2SiO4 systems under pressures 0 GPa and 40 GPa. We clarify structure of amorphous Mg2SiO4 at 0 and 40 GPa and compared with the one of Mg2SiO4 at liquid state. Especially, the origin of sub-peaks in radial distribution function of O-O, Si-Si and Mg-Mg pairs is explained clearly. The change of radial distribution functions, coordination number and the number of all types of bonds including the corner-, edge- and face-sharing bonds is also discussed in detail in this paper. Keywords: Molecular dynamics simulation, magnesium silicate, structure. 1. Introduction Magnesium silicate (Mg2SiO4) is one of the most abundant materials of the Earth’s upper mantle [1, 2]. It is also an important component in many high technology applications [3]. Mg2SiO4 system has been extensively investigated for a long time by both experiment (X-ray diffraction, nuclear magnetic resonance, Raman spectroscopy technology) [4-6] and simulation (Molecular Dynamics, Monte Carlo) [1-3, 7-11]. Knowledge of structure of Mg2SiO4 system in both solid and liquid states at different temperature and pressure conditions is necessary for understanding about thermal change of the Earth as well as application in the process of new material fabrication technology. The X-ray diffraction and Neutron scattering experimental results showed that [8] Si atoms in Mg2SiO4 glass has mainly 4 coordinated oxygens and the mean bond length of Si-O is about 1.60 Å. Meanwhile the Mg atoms are surrounded 5 oxygens and the Mg-O bond length is about 2.0 Å. Using nuclear magnetic resonance [4, ________ Corresponding author. Email address: lan.maithi@hust.edu.vn https//doi.org/ 10.25073/2588-1124/vnumap.4520 38 M.T. Lan, N.T. Thao / VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 39 5] authors indicated that the coordination number of Mg is 5 and 6. The simulation results [2, 10, 11] also showed that structure Mg2SiO4 comprise basic structural unit TOn (T= Si, Mg; n is the number of oxygens that surrounded T atoms). There is change of the coordination number of Si and Mg atoms and intermediate range order structure in magnesium silicate melts under compression [2]. Molecular dynamics simulation of MgSiO3 liquid [12, 13] clarified structural organization, network topology as well as the degree of polymerization under compression. In this work, we clarify structure of amorphous Mg2SiO4 at 0 and 40 GPa and compared with the one of liquid Mg2SiO4. Especially, the origin of sub- peaks in radial distribution function of O-O, Si-Si and Mg-Mg pairs also explain via analysis the TOn units as well as the corner-, edge- and face-sharing bonds between adjacent structural units TOn. 2. Calculation Method Molecular dynamics simulations are used to construct Mg2SiO4 models containing several thousand atoms. Simulation method is recognized as a numerical empirical method and plays a close link between 25 6 Si-O Mg-O Mg SiO at 0 GPa Mg SiO at 0 GPa a) 2 4 2 4 amorphous 600K a) amorphous 600K 5 20 liquid 3500K liquid 3500K 4 15 (r) Mg-O (r) g 3 Si-O g 10 2 5 1 0 0 0 2 4 6 8 0 2 4 6 8 r (Å) r (Å) 25 6 Si-O Mg SiO at 40GPa b) Mg-O Mg SiO at 40 GPa 2 4 2 4 b amorphous 600K amorphous 600K ) 20 5 liquid 3500K liquid 3500K 4 15 (r) (r) 3 Si-O Mg-O g 10 g 2 5 1 0 0 0 2 4 6 8 0 2 4 6 8 r (Å) r (Å) Figure 1. The radial distribution function of Si-O Figure 2. The radial distribution function of Mg-O pair at both states at 0 GPa (a) and 40 GPa (b) pair at both states and at 0 GPa (a) and 40 GPa (b) 40 M.T. Lan, N.T. Thao / VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 two theoretical and empirical methods. The initial configuration of the sample is built by randomly placing 4998 Si, Mg and O atoms in a simulation box with the condition that no two atoms are too close together. The motion of atoms in the model follows the Newton’s equation of motion. We used the Verlet algorithm to integrate the equation of motion, the Ewald-Hansen approximation technique applied to significantly reduce the time taken to calculate the Coulomb interaction at a distance. The Oganov potentials are used to construct Mg2SiO4 models [11, 12]. Under the influence of the interaction force, the atoms will shift to the equilibrium po ... .0 1.0 0.5 0.5 0.0 0 2 4 6 8 0.0 r (Å) 2 4 6 8 r (Å) Figure 3. The radial distribution function of O-O Figure 4. The radial distribution function of Si-Si pair at both states at 0 GPa (a) and 40 GPa (b). pair at both states at 0 GPa (a) and 40 GPa (b). M.T. Lan, N.T. Thao / VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 41 3. Results and Discussion First, we calculate radial distribution function of T-O, O-O and T-T pairs at both states and at 0 GPa and 40 GPa. Regarding to Si-O pair, figure 1a shows that at 0 GPa, the position of the first peak at amorphous and liquid states is about 1.62 Å. It means that Si-O bond length is almost not dependent on temperature. At 40 GPa, the position of the first peak at liquid state tends to shift slightly to the left 3.5 2.5 Si-Mg Mg SiO at 0 GPa Mg-Mg Mg SiO at 0 GPa 2 4 a) 2 4 3.0 amorphous 600K amorphous 600K a) liquid 3500K 2.0 liquid 3500K 2.5 (r) 1.5 Si-Mg 2.0 (r) g Mg-Mg 1.5 g 1.0 1.0 0.5 0.5 0.0 0.0 0 2 4 6 8 10 0 2 4 6 8 10 r (Å) r (Å) 3.5 2.5 Si-Mg Mg-Mg Mg SiO at 40 GPa Mg SiO at 40 GPa b) 2 4 3.0 2 4 amorphous 600K b) amorphous 600K 2.0 liquid 3500K liquid 3500K 2.5 (r) (r) Si-Mg 1.5 g 2.0 Mg-Mg g 1.5 1.0 1.0 0.5 0.5 0.0 0.0 0 2 4 6 8 10 0 2 4 6 8 10 r (Å) r (Å) Figure 5. The radial distribution function of Si-Mg Figure 6. The radial distribution function of Mg-Mg pair at both states at 0 GPa (a) and 40 GPa (b). pair at both states at 0 GPa (a) and 40 GPa (b). compare to the one at amorphous state and at 0 GPa. The Si-O bond length at 40 GPa is smaller than the one at 0 GPa (see figure 1b). Besides at the same pressure, the height of the first peak in liquid state is smaller than the one in amorphous states. The full width at half maximum of the first peak in liquid state is larger than the one in amorphous states. It means that the degree of structural order in Mg2SiO4 at amorphous is higher than the one in liquid state. The degree of structural order in Mg2SiO4 at 40 GPa is higher than the one at 0 GPa. Regarding to Mg-O, figure 2a indicates that the Mg-O bond length in amorphous is about 1.94 Å and the Mg-O bond length is longer than the one in liquid state. Under compression, the first peaks in both states shift to the left, it means that the Mg-O length decreases as pressure increases. For O-O pair, it can be seen that there are two peaks in the O-O radial distribution 42 M.T. Lan, N.T. Thao / VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 function in amorphous state at 0 GPa (see figure 3a). This is not appearance in amorphous state at 40 GPa and in liquid state at 0 and 40 GPa (see figure 3a, b). The main peak is about 2.6 Å and the sub- peak is about 3.02 Å. The position of the first peak of O-O pair shifts to left, thus the O-O bond length decreases when pressure increases from 0 to 40 GPa. Figure 4 indicates the Si-Si radial distribution function at both states. The results show that at 0 GPa and in both states, it has the first peak at location of about 3.10 Å. However, at 40 GPa, the Si-Si radial distribution function in amorphous state appears a shoulder at around 2.82 Å. For Si-Mg pair (see figure 5), the Si-Mg bond distance decreases strongly at both states as pressure increases. At 0 GPa, the Si-Mg bond distance in amorphous and liquid states is about 3.20 Å and 3.40 Å at 0 GPa, respectively. At 40 GPa, these bond distances in amorphous and liquid states is about 2.80 Å and 2.60 Å, respectively. In the Mg-Mg pair radial distribution function, it appears a shoulder at location of 3.80 Å in amorphous state at 40 GPa. Meanwhile, the radial distribution function of Mg-Mg pair in both states at 0 GPa and in liquid state at 40 GPa has only the main first peak at around 2.8 – 3.2 Å. The Mg-Mg bond distances at 0 GPa are larger than the one at 40 GPa. Next, we calculate distribution of the coordination number for simulated Mg2SiO4 system at both states and at 0 and 40 GPa, it showed on table 1. Table 1. Distribution of the coordination number for simulated Mg2SiO4 system at both states and at 0 and 40 GPa; Cx are the fraction of SiOx units (x=4-6), Dy are the fraction of MgOy units (y=3-8) Fraction amorphous state liquid state (%) 0 GPa 40 GPa 0 GPa 40 GPa C4 92.20 9.90 99.20 10.79 C5 5.60 46.90 0.80 46.61 C6 0.10 42.30 0.00 42.59 D3 14.20 0.00 0.45 0.00 D4 39.90 0.10 32.67 0.01 D5 32.90 3.50 49.58 2.53 D6 10.40 24.70 16.87 39.37 D7 1.20 41.50 0.43 42.40 D8 0.10 24.30 0.00 15.69 The results show that, at amorphous state there are percentage of SiO4 units is 92.20% at 0 GPa. At 40 GPa, the fraction of SiO4 decreases strongly while the fraction of SiO5 and SiO6 increase sharply. It means that there is structural phase transition from SiO4 to SiO5 and SiO6 units under compression. The fraction of SiOx units in Mg2SiO4 in liquid states is similar to the one in amorphous states and at both pressure 0 and 40 GPa. Relating to MgOy units, it can be seen that there is difference about the percentage of structural units MgOy at amorphous and liquid states as well as at different pressure. Namely, at 0 GPa, the fraction of MgO3, MgO4 and MgO5 units is dominant in amorphous Mg2SiO4, meanwhile the fraction of MgO4, MgO5 and MgO6 units is dominant in liquid Mg2SiO4. At 40 GPa, percentage of MgO6, MgO7 and MgO8 is dominant in both states. The above analysis illustrates that the structure of amorphous Mg2SiO4 is built mainly by the SiO4, MgO3, MgO4 and MgO5 and a number of small SiO5 network at 0 GPa. Meanwhile, the structure of liquid Mg2SiO4 is built mainly by the SiO4, M.T. Lan, N.T. Thao / VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 43 MgO4, MgO5 and MgO6 network. At 40 GPa, the network structure of Mg2SiO4 at both states consists of SiO5, SiO6, MgO6, MgO7 and MgO8 network. These SiOx, MgOy structural units can be link to each other via oxygens to form network structure of Mg2SiO4 system that visualized in figure 7 and 8. Figure 7. The snapshot of network structure of Mg2SiO4 at 0 GPa and at both states: amorphous (left) and liquid (right) Figure 8. The snapshot of network structure of Mg2SiO4 at 40 GPa and at both states: amorphous (left) and liquid (right). It can be seen that the atoms tend to arrange more orderly at 40 GPa compare to 0 GPa. The O-O bond distance depends on the O-Si-O and O-Mg-O bond angle in the SiOx and MgOy units, respectively. 44 M.T. Lan, N.T. Thao / VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 The previous studies [2, 13, 14] indicated that magnesium silicate system at 0 GPa has the O-Si-O and O-Mg-O bond angle are different, around 105-1100 and 85-900 degree, respectively. Meanwhile, at high pressure (40GPa) or in liquid Mg2SiO4, the O-Si-O and O-Mg-O bond angle are almost the same. Thus, there are only two O-O bond distances in amorphous Mg2SiO4 at 0 GPa. This leads to existence of sub- peak in the O-O radial distribution function in amorphous Mg2SiO4 at 0 GPa. Furthermore, in amorphous Mg2SiO4 at 40 GPa, MgOy are mainly MgO6, MgO7 and MgO8 units. The Mg-O-Mg bond angle distribution has a peak at around 80 and a shoulder at around 150 degree [14]. This is original of appearance of sub-peak in the Mg-Mg pair radial distribution function in amorphous Mg2SiO4 at 40 GPa. We continue studying all type of links between adjacent SiOx units, adjacent MgOy units and adjacent SiOx and MgOy units in Mg2SiO4 system. We found that there are three type of links including the corner-, edge- and face-sharing bonds. The number of the corner-, edge- and face-sharing bonds is showed in Table 2. Table 2. The number of corner-, edge- and face-sharing bonds (denoted Ncorner, Nedge and Nface respectively) between adjacent TOn units (T=Si,Mg) amorphous state liquid state Structural units 0 GPa 40 GPa 0 GPa 40 GPa Ncorner 487 983 535 894 SiOx-SiOx Nedge 0 182 0 11 Nface 0 29 0 46 Ncorner 3574 4483 3222 4609 MgOy-MgOy Nedge 1746 2651 1052 2511 Nface 267 1407 152 1232 Ncorner 4077 3980 2857 4080 SiOx-MgOy Nedge 367 2402 460 2014 Nface 2 488 15 463 It can be seen that at 0 GPa, links between two adjacent SiOx units are corner-sharing bonds in amorphous and liquid states. The number of corner-sharing bonds at amorphous and liquid state is 487 and 535, respectively. At 40 GPa, in both states, the adjacent SiOx units link each other by three types of bonds. The number of corner-sharing bonds is also dominant. Note that, the number of edge-sharing bonds in amorphous Mg2SiO4 at 40 GPa is the largest. As above mentioned, the structure of amorphous Mg2SiO4 is mainly build by SiO4 units at 0 GPa and SiO5, SiO6 units at 40 GPa. It means that links between two adjacent SiO4 units are corner-sharing bonds, meanwhile links between two adjacent SiO5, SiO6 units are corner-, edge-, and face- sharing. Thus, the appearance of sub-peak in Si-Si radial distribution function at around 2.82 Å at 40 GPa due to existence of the edge-, face-sharing bonds. For the adjacent MgOy units, they link to each other by all three types. At 0 GPa, the number of corner-, edge-, and face- sharing is 3574, 1746 and 267 in amorphous Mg2SiO4 and 3222, 1052 and 152 in liquid Mg2SiO4, respectively. As pressure increases, the number of all three types bonds increases. At 40 GPa, the number of corner-, edge-, and face- sharing is 4483, 2651 and 1407 in amorphous Mg2SiO4 and 4609, 2511 and 1232 in liquid Mg2SiO4, respectively. Similar to the results for the adjacent MgOy units, the links between adjacent SiOx and MgOy units consist of all three types of bonds and the number of all three types bonds increases as increasing pressure. M.T. Lan, N.T. Thao / VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 45 4. Conclusion We find that the structure of Mg2SiO4 consists of basic structural units TOn (T=Si, Mg; n=3-8). These TOn link to each other through oxygen atoms to form network structure. The T-O coordination number increases as pressure increases. The amorphous Mg2SiO4 comprises mainly SiO4, MgO3, MgO4 and MgO5 and a number of small SiO5 network at 0 GPa. Meanwhile, the structure of liquid Mg2SiO4 comprises SiO4, MgO4, MgO5 and MgO6 network. At 40 GPa, the network structure of Mg2SiO4 at both states consists of SiO5, SiO6, MgO6, MgO7 and MgO8 network. In amorphous and liquid Mg2SiO4 system, the links between the adjacent SiOx units are mainly corner- and edge-sharing bonds. Meanwhile the links between the adjacent MgOy units, the adjacent SiOx and MgOy units are all types of bonds including corner-, edge-, and face- sharing bonds. The appearance of the sub-peaks in radial distribution function of Si-Si pair due to existence of the number of significantly edge- and face-sharing bonds in amorphous Mg2SiO4 at 40 GPa. The existence of the sub-peak in the O-O radial distribution function in amorphous Mg2SiO4 at 0 GPa is due to difference of the O-Si-O and O-Mg-O bond angle. The original the sub-peak in the Mg-Mg pair radial distribution function in amorphous Mg2SiO4 at 40 GPa relates to existence of two peak in the Mg-O-Mg bond angle distribution in MgOy units. Acknowledgments This research is funded by Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 103.05-2018.37. References [1] D. B. Ghosh, B. B. Karki, First principles simulations of the stability and structure of grain boundaries in Mg2SiO4 forsterite, Phys Chem Minerals 41 (2014), 163-171. https://doi.org/10.1007/s00269-013-0633-1. [2] O. Adjaoud, G. Steinle-Neumann and Sandro Jahn, Mg2SiO4 liquid under high pressure from molecular dynamics, Chemical Geology 256 (2008), 185–192. https://doi.org/10.1016/j.chemgeo.2008.06.031. [3] S. Guan, X. Zhang, Z. P. Liu, Energy landscape and crystal to crystal transition of ternary silicate Mg2SiO4, J. Phys. Chem. C 120 (2016) 25110-25116. https://doi.org/10.1021/acs.jpcc.6b08942 [4] K. Shimoda, Y. Tobu, M. Hatakeyama, T. Nemoto, K. Saito, Structural investigation of Mg local environments in silicate glasses by ultra-high field 25Mg 3QMAS NMR spectroscopy. Am Mineral 92 (2007), 695–698. https://doi.org/10.2138/am.2007.2535. [5] S. Sen, H. Maekawa, G.N Papatheodorou, Short-range structure of invert glasses along the pseudo-binary join 29 25 MgSiO3-Mg2SiO4: results from Si and Mg MAS NMR Spectroscopy, J Phys Chem B 113 (2009),15243–15248. https://doi.org/10.1021/jp9079603. [6] C. J. Benmore, E. Soignard, M. Guthrie, S. A. Amin, J. K. R. Weber, K. McKiernan,M. C. Wilding, J.L. Yarger, High pressure x-ray diffraction measurements on Mg2SiO4 glass, J. Non-Cryst. Solids 357 (2011), 2632-2636. https://doi.org/10.1016/j.jnoncrysol.2010.12.064. [7] N. Tomioka, T. Okuchi, A new high-pressure form of Mg2SiO4 highlighting diffusion less phase transitions of olivine, Sci Rep 7(1) (2017), 17351. https://doi.org/10.1038/s41598-017-17698-z. [8] M. C. Wilding, C. J. Benmore, J. A. Tangeman, S. Sampath, Coordination changes in magnesium silicate glasses, Europhys. Lett. 67 (2004), 212-218. https://doi.org/10.1209/epl/i2003-10286-8. [9] J. D. Kubicki, A. C. Lasaga, Molecular dynamics simulations of pressure and temperature effects on MgSiO3 and Mg2SiO4 melts and glasses, Phys Chem Miner 17 (1991), 661–673. https://doi.org/10.1007/BF00202236. [10] J. S. Frank, S. G. Mark, D. Nevins, Structure, thermodynamic and transport properties of liquid MgSiO3: Comparison of molecular models and laboratory results, Geochimica et Cosmochimica Acta 75 (2011), 1272-1296. https://doi.org/10.1016/j.gca.2010.12.004. 46 M.T. Lan, N.T. Thao / VNU Journal of Science: Mathematics – Physics, Vol. 37, No. 1 (2021) 38-46 [11] P. K. Nico, L. Stixrude, B. K. Bijaya, Thermodynamics, structure, dynamics, and freezing of Mg2SiO4 liquid at high pressure, Geochimica et Cosmochimica Acta 72 (2008), 1427–1441. https://doi.org/10.1016/j.gca.2007.12.019. [12] L. T. San, N. V. Hong, T. Iitaka, P. K. Hung, Structural organization, micro-phase separation and polyamorphism of liquid MgSiO3 under compression, Eur. Phys. J. B 89 (2016) 73. https://doi.org/10.1140/epjb/e2016-60740-4. [13] N. T. Thao, N. T. Trang, T. D. Hinh, L. V. Vinh, Molecular dynamics simualtions of structural and mechanical properties in MgSiO3 glass, Phys. Status Solidi B (2019), 1900215. https://doi.org/10.1002/pssb.201900215. [14] N. V. Hong, M. T. Lan, P. K. Hung, Structure and dynamics of liquid MgO under high pressure, High Pressure Research 32 (4) (2012), 509-523. https://doi.org/10.1080/08957959.2012.736506.
File đính kèm:
 structure_analysis_of_amorphous_and_liquid_magnesium_silicat.pdf
structure_analysis_of_amorphous_and_liquid_magnesium_silicat.pdf

