Solving heat transfer problem in ultrasonic welding based on hybrid spline difference method

 ISSN 2354-0575
 SOLVING HEAT TRANSFER PROBLEM IN ULTRASONIC WELDING
 BASED ON HYBRID SPLINE DIFFERENCE METHOD
 Thi-Thao Ngo, Ngoc-Thanh Tran, Van-The Than
 Hung Yen University of Technology and Education
 Received: 05/08/2019
 Revised: 23/08/2019
 Accepted for publication: 03/09/2019
Abstract:
 A Hybrid Spline Difference Method is developed to solve a nonlinear equation of welding problem 
in ultrasonic welding. It is shown that the method has a computational procedure as simply as the finite 
difference method. In addition, the proposed method can simplify complexity of the traditional spline 
method calculation, and increase accuracy of the first and second derivatives of space from O(Tx 2) of 
finite difference method to O(Tx 4). According to the calculated temperature distribution in the work pieces, 
during the ultrasonic welding process, the proposed method illustrated that not only its precision is greatly 
enhanced, but also its concept is very similar to that of the finite difference method. Based on analysis 
results, it was concluded that the simple and high-accuracy hybrid spline difference method has a strong 
potential to substitute the traditional finite difference method.
Keywords: ultrasonic metal welding, hybrid spline difference method, finite difference method.
1. Introduction addition, almost previous analyses of heat and mass 
 Ultrasonic welding (USW) is a process for transfer used the FDM because of its simple concept 
joining similar and dissimilar material samples and easy operation; however, the FDM’s solutions 
in various industries. Heat generated at welding rarely have high accuracy. On the contrary, with 
interface during the welding process is due to characteristics of smoothness and continuity, the 
plastic deformation and friction from a motion spline method has higher numerical precision than 
between two contacting work pieces’ surface [1]. that of FDM; thus, numerical solution of spline [11-
The heat generation plays an important role in 14] has been widely applied. However, the spline 
welding process, generally, because it significantly method has a complicated calculation procedure 
influences on temperature distribution in the weld and an unsolved problem of determination of the 
parts. optimal parameters. Therefore, in recent years 
 Several researchers have studied temperature Wang et al. [15-18] constructed a simple procedure 
distributions at the interface and in the work pieces of solving the spline difference in a discretization 
as well as in the horn (sonotrode). The temperature approach similar to finite difference. 
was predicted by using ANSYS finite element This study develops the skill of hybrid spline 
models [2-4]. Thermal conductivity and specific that makes the first order and second order numerical 
heat in these researches were considered as constant, differential accuracies reach O(∆x)4 at the same 
it means the governing heat transfer equations were time. The nonlinear equation of welding problem in 
established are only linear equation. ultrasonic welding is analyzed to validate a simple 
 Actually, many numerical methods have been and high-accuracy characteristic of proposed hybrid 
proposed for solving heat transfer problems. The spline difference method (HSDM).
Finite Difference Method (FDM) has been used to 
solve heat transfer of complex geometric shapes [5, 2. Mathematical Structure
6]. In order to increase the accuracy of numerical 2.1. Construction of Hybrid Spline Difference 
method, the hybrid differential transformation Method
method, - Taylor transformation method [7, 8], the 2.1.1. Original parametric spline
boundary element method [9] as well as the finite In numerical methods, a single polynomial is 
volume method [10] can be effectively used. In usually used to approximate an arbitrary function, 
Khoa học & Công nghệ - Số 23/Tháng 9 - 2019 Journal of Science and Technology 13
ISSN 2354-0575
and it is found that this approach was sometime 2.1.2. Basic conception of spline difference
unsatisfactory. To overcome this deficiency, the In the previous spline method, Eqs. (4) 
functional region can be divided into many sub- are mainly solved using Eq. (4) combined with 
regions which are presented by polynomials the differential equation itself. This procedure is 
and simple functions. Wang and Kahawita [11] more complicated and it is quite different from 
hypothesized a traditional cubic spline function is the conventional FDM. Thus, in this study, an 
as a simple cubic polynomial such that its curvature approximate function of the differential equation is 
after second differential is a linear relationship as adopted to construct multiple different parametric 
 zzmmx - zzmm- x splines, zcxx- i Dx , , expressed as
 ii__ii-1 = ii `j
 - - (1) N+1
 xxi-1 xxi xx- i
 zcxp,,= / i zc (5)
 where z x and z x are the cubic spline _ i i =-1 b Dx l
 i-1 _i i _i
approximation curves i ... M is into two steps.
applicable to determine temperature in ultrasonic Step 1: solve x direction.
 2
welding process, the 2D welding model is considered ppij+-11,,-+ij ppij,,mmij-+11-+ppij,,mij
 kT() +
in this study. According to the conservation of heat f Tx2 12 p
energy and Fourier’s Law, the partial differential 
 2kT()ppij+-11,,--ij ppij+-11,,ij
 + # + t ()
heat transfer equation 2T 22TTx e x CTpwV o 
 2
 2 2T 222T 2kT()2T 2kT()2T 2 2 () 2
 kT() ++kT() + ()2 T kT 2T (,)
 2x2 2y2 2T 2x 2T d 2y n =-kT 2 --2 2 qxw y
 b l e 2y oij, T d y nij,
 2
++(,)(t ) T = 0 (12)
 qxwpyCTVw 2x
 (9) Step 2: solve y direction.
 2
 and accompanied boundary conditions ppij,,+-11-+ij ppij,,mmij-+11-+ppij,,mij
 kT() +
 () f Ty2 12 p
Tx,yT==3 at xxmaxmand xx= in (10a)
 2
 () 2
 2 () 2kT ppij,,+-11- ij 2 T
 () Tx,y + =-kT()
-=kT hT-=Ta3 ty ymax 2T f 2Ty p 2
 2y _i (10b) d 2x nij,
 2 () 2 ()
 Tx,y 0 kT 2T 2T () (,)
and ==at yymin -+tCTpwVq- w xy
 2y 2T 2x b 2x lij,
 (13)
 where T and T3 are the temperatures in 
the specimen and surrounding temperature, Eqs. (12) and (13), can be further rearranged 
 into the following forms
respectively; t is the density, k(T) and Cp(T) are the 
 ++ = (14)
thermal conductivity and heat capacity and xmax, xmin TAiipT-+11,,jiBpij TCiipT,jiD
and ymax, ymin describe boundary dimensions of the 
 In Eq. (14) TAi, TBi, TCi and TDi , where i = 1, 
work pieces in the x and y direction, respectively. 2, are known values, the iteration can be performed 
 The thermal conductivity and heat capacity to determine new pi,j by using the Thomas algorithm 
are functions of temperature, thus, in this problem 
 [20] after p-1, j and pNji +1, are removed at step 1, 
becomes nonlinear. In Eq. (9) qw(x,y) is the heat pi,-1 and piN, j +1 are eliminated at step 2. Then, 
generated during the welding process. The heat Eq. (8) can be used to directly obtain the calculation 
generated at the weld interface in the welding process discrete function T(x,y) and its first- and second-
is due to plastic deformation and friction from two order derivatives. 
work piece faces. According to Koellhoffer et al. 
[1] deformational heat generation is distinctively 3. Numerical Results and Discussion
considered small in comparison to frictional 3.1. Example 1
heat generation for typical process parameters in The spline method described is used to solve 
USMW. Therefore, the temperature increase due the following differential equation:
 2 2
to deformation is negligible. The frictional heat is 2 T 2 T 2T 2T 2
 +++=- 2rrsinx()siny()r
indicated in: 2x2 2y2 2x 2y
 2 ++rrcosx()siny()rrsinx()rrcosy()
 , npFfNw0
 qxw y = (11)
 _i wlc (15a)
Khoa học & Công nghệ - Số 23/Tháng 9 - 2019 Journal of Science and Technology 15
ISSN 2354-0575
 With following boundary conditions: Table 2. A comparison of numerical error and 
 ()01() ()01()0 computer time between the proposed method and 
Ty,,====Ty Tx,,Tx (15b)
 with 01##x and 01##y the finite difference method
 Eq. (16) has an exact solution of Grids Error Computer time (s)
 N # N Finite The Finite The 
 ()= ()rr() i j
 Tx,ysin xsin y (16) difference present difference present
 Using the discretization and solving procedure 5 # 5 0.008932 5.077E-05 0.001 0.02
described in above section, the calculation steps are 
 10 # 10 0.002759 5.251E-06 0.009 0.042
as below. First, solving in x direction:
 20 # 20 0.0007638 4.507E-07 0.122 0.382
 2 # 0.0002008 3.362E-08 1.622 5.393
 ppij+-11,,-+ij pij,,ppij+-11- ij, 40 40
 ++TT
f Tx2 xx p 2Tx 80 # 80 5.148E-05 2.316E-09 21.706 80.196
 # 1.303E-05 1.585E-10 290.37 1211.5
 22 2 160 160
=- T --T 2rr2 ()()r
 2 2y sinxsiny
 e 2y oij, As shown in in Table 2, the numerical error is 
 ()() () () 160 160
++rrcosxsinyrrsinxrrcosy 1.303E-05 when grid points of NNij##= 
 (17a) was selected for solution using FDM. When the 
 Second, solving in y direction proposed method is used, the error can rea ch 
 ##
 2 5.077E-05 with grid points of NNij= 5 5 and 
 ppij,,+-11-+ij pij,,ppij+-11- ij,
 ++TT the calculation time can be reduced from 290.37 to 
f Ty2 yy p 2Ty
 0.02 s. The results indicate that the presented method 
 2
 2 T 2T 2
=- --2rrsinx()siny()r is superior to both FDM and parametric spline 
 2 2 2x
 d x nij, method and can rapidly reduce the computer time.
++rrcosx()siny()rrsinx()rrcosy()
 (17b) 3.2. Example 2
 Example 2 considers solving the nonlinear 
Table 1. Error comparison of proposed method, 
 equation of ultrasonic welding problem as described 
 FDM, and parametric spline method
 by Eqs. (9), (10a) & (10b). The welding conditions 
 # 32 10-6
 Ni Nj Finite Parametric The are set as sonotrode amplitude, p0 = # m, 
 Difference spline present = 20000
 (,) (,) welding frequency, fw , and normal force, 
 ab ab hybrid 1600
 FNN = . 
 " (,01/)2 " (,112512 ) Spline
 Because the governing equation is nonlinear, 
 5 # 5 0.008932 0.0006458 5.077E-05 the exact analytic solution is simulated by 20 times 
 10 # 10 0.002759 0.0002039 5.251E-06 the grid point numbers in the case of an unavailable 
 20 # 20 0.0007638 5.718E-05 4.507E-07 analytic solution.
 40 # 40 0.0002008 1.508E-05 3.362E-08
 80 # 80 5.148E-05 3.869E-06 2.316E-09
 160 # 160 1.303E-05 9.796E-07 1.585E-10
 Table 1 shows a comparison of numerical 
errors obtained for three methods i.e. the proposed 
method, the parametric spline and the FDM. It can 
be clearly seen from Table 1 that the results obtained 
by HSDM have far higher numerical precision than 
those obtained by other methods. In addition, the 
speed of decreasing error of the HSDM shown to 
decrease significantly faster with increasing the
grids number than that of the FDM and parametric 
spline methods. Additionally, numerical error and 
computing time comparison of the HSDM and 
FDM are shown in Table 2. Fig.1. Distribution of the calculated temperature
16 Khoa học & Công nghệ - Số 23/Tháng 9 - 2019 Journal of Science and Technology
 ISSN 2354-0575
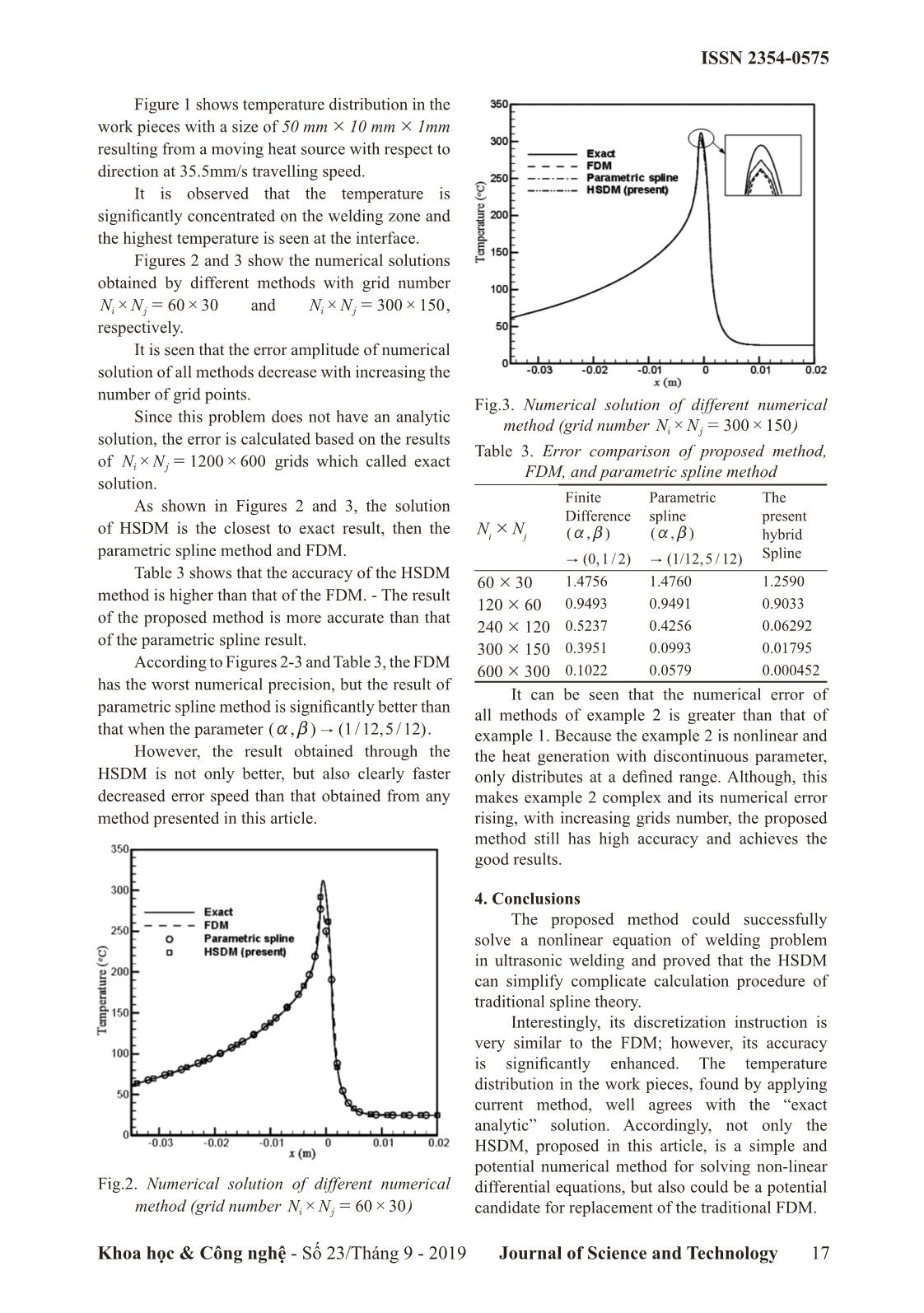
 Figure 1 shows temperature distribution in the 
work pieces with a size of 50 mm # 10 mm # 1mm 
resulting from a moving heat source with respect to 
direction at 35.5mm/s travelling speed.
 It is observed that the temperature is 
significantly concentrated on the welding zone and 
the highest temperature is seen at the interface.
 Figures 2 and 3 show the numerical solutions 
obtained by different methods with grid number 
 60 30 300 150
 NNij##= and NNij##= , 
respectively. 
 It is seen that the error amplitude of numerical 
solution of all methods decrease with increasing the 
number of grid points.
 Fig.3. Numerical solution of different numerical 
 Since this problem does not have an analytic 300 150
 method (grid number NNij##= )
solution, the error is calculated based on the results 
 Table 3. Error comparison of proposed method, 
of NN##= 1200 600 grids which called exact 
 ij FDM, and parametric spline method
solution. 
 Finite Parametric The 
 As shown in Figures 2 and 3, the solution 
 Difference spline present
of HSDM is the closest to exact result, then the N # N (,ab) (,ab)
 i j hybrid 
parametric spline method and FDM. " (,01/)2 " (,1/12 51/)2 Spline
 Table 3 shows that the accuracy of the HSDM 
 60 # 30 1.4756 1.4760 1.2590
method is higher than that of the FDM. - The result 
 120 # 60 0.9493 0.9491 0.9033
of the proposed method is more accurate than that 
 240 # 120 0.5237 0.4256 0.06292
of the parametric spline result. 
 300 # 150 0.3951 0.0993 0.01795
 According to Figures 2-3 and Table 3, the FDM 
 600 # 300 0.1022 0.0579 0.000452
has the worst numerical precision, but the result of 
 It can be seen that the numerical error of 
parametric spline method is significantly better than all methods of example 2 is greater than that of 
 (,)(" 11/,25/)12
that when the parameter ab . example 1. Because the example 2 is nonlinear and 
 However, the result obtained through the the heat generation with discontinuous parameter, 
HSDM is not only better, but also clearly faster only distributes at a defined range. Although, this 
decreased error speed than that obtained from any makes example 2 complex and its numerical error 
method presented in this article. rising, with increasing grids number, the proposed 
 method still has high accuracy and achieves the 
 good results.
 4. Conclusions
 The proposed method could successfully 
 solve a nonlinear equation of welding problem 
 in ultrasonic welding and proved that the HSDM 
 can simplify complicate calculation procedure of 
 traditional spline theory. 
 Interestingly, its discretization instruction is 
 very similar to the FDM; however, its accuracy 
 is significantly enhanced. The temperature 
 distribution in the work pieces, found by applying 
 current method, well agrees with the “exact 
 analytic” solution. Accordingly, not only the 
 HSDM, proposed in this article, is a simple and 
 potential numerical method for solving non-linear 
Fig.2. Numerical solution of different numerical differential equations, but also could be a potential 
 ##60 30
 method (grid number NNij= ) candidate for replacement of the traditional FDM.
Khoa học & Công nghệ - Số 23/Tháng 9 - 2019 Journal of Science and Technology 17
ISSN 2354-0575
References
 [1]. S. Koellhoffer, J. W. Gillespie, S. G. Advani, and T. A. Bogetti, “Role of friction on the thermal 
 development in ultrasonically consolidated aluminum foils and composites,” Journal of Materials 
 Processing Technology, 2011, vol. 211, pp. 1864-1877.
 [2]. K. S. Suresh, A. R. Rani, K. Prakasan, and R. Rudramoorthy, “Modeling of temperature distribution 
 in ultrasonic welding of thermoplastics for various joint designs,” Journal of Materials Processing 
 Technology, 2007, vol. 186, pp. 138-146.
 [3]. S. Elangovan, S. Semeer, and K. Prakasan, “Temperature and stress distribution in ultrasonic 
 metal welding—An FEA-based study,” Journal of Materials Processing Technology, 2009, vol. 209, 
 pp. 1143-1150.
 [4]. M. R. Rani and R. Rudramoorthy, “Computational modeling and experimental studies of the 
 dynamic performance of ultrasonic horn profiles used in plastic welding,”Ultrasonics , Mar 2013, vol. 
 53, pp. 763-772.
 [5]. B. S. Chen, L. Y. Tong, Y. X. Gu, H. W. Zhang, and O. Ochoa, “Transient heat transfer analysis 
 of functionally graded materials using adaptive precise time integration and graded finite elements,” 
 Numerical Heat Transfer Part B-Fundamentals, Feb 2004, vol. 45, pp. 181-200.
 [6]. D. Sharanjeet and K. Sheo, “A Comparative Study of Numerical Techniques for 2D Transient 
 Heat Conduction Equation Using Finite Element Method,” Int. J. Res. Rev. Appl. Sci., 2009, vol. 1, 
 pp. 38–46.
 [7]. C. Y. Lo, “A Study of Two-Step Heat Conduction in Laser Heating Using the Hybrid Differential 
 Transform Method,” Numerical Heat Transfer Part B-Fundamentals, 2011, vol. 59, pp. 130-146.
 [8]. C. Y. Lo and B. Y. Chen, “Application of Hybrid Differential Transform/Control-Volume Method 
 to Hyperbolic Heat Conduction Problems,” Numerical Heat Transfer Part B-Fundamentals, 2009, 
 vol. 55, pp. 219-231.
 [9]. M. Dondero, A. P. Cisilino, J. M. Carella, and J. P. Tomba, “Effective thermal conductivity of 
 functionally graded random micro-heterogeneous materials using representative volume element and 
 BEM,” International Journal of Heat and Mass Transfer, Aug 2011, vol. 54, pp. 3874-3881.
 [10]. H. B. Luan, H. Xu, L. Chen, D. L. Sun, Y. L. He, and W. Q. Tao, “Evaluation of the coupling 
 scheme of FVM and LBM for fluid flows around complex geometries,”International Journal of Heat 
 and Mass Transfer, Apr 2011, vol. 54, pp. 1975-1985.
 [11]. P. Wang and R. Kahawita, “Numerical Integration of Partial Differential Equations Using Cubic 
 Splines,” Int. J. Comput. Math., 1983, vol. 13, pp. 271-286.
 [12]. C. C. Wang, “Applying the Differential Equation Maximum Principle with Cubic Spline Method 
 to Determine the Error Bounds of Borced Convection Problems,” Int. Commun. Heat Mass Transfer, 
 2010, vol. 37, pp. 147–155.
 [13]. C. C. Wang and Z. Y. Lee, “Uniform-Parameter Spline Method for Solving Non-Fourier Heat 
 Conduction Problems,” Numerical Heat Transfer Part B-Fundamentals, 2009, vol. 56, pp. 293-306.
 [14]. H. F. Ding and Y. X. Zhang, “Parameters spline methods for the solution of hyperbolic equations,” 
 Applied Mathematics and Computation, Oct 15 2008, vol. 204, pp. 938-941.
 [15]. C. C. Wang, L. P. Chao, and W. J. Liao, “Hybrid Spline Difference Method (HSDM) for Transient 
 Heat Conduction,” Numerical Heat Transfer Part B-Fundamentals, 2012, vol. 61, pp. 129-146.
 [16]. C. C. Wang, H. Chen-Hung, and D. J. Yang, “Hybrid Spline Difference Method for Steady-State 
 Heat Conduction,” Numerical Heat Transfer Part B-Fundamentals, 2011, vol. 60, pp. 472-485.
 [17]. C. C. Wang, W. J. Liao, and C. Y. Yang, “Hybrid Spline Difference Method for Heat Transfer 
 and Thermal Stresses in Annular Fins,” Numerical Heat Transfer, Part B: Fundamentals, 2013, vol. 
 64, pp. 71–88.
 [18]. C. C. Wang, W. J. Liao, and Y. S. Hsu, “Hybrid spline difference method for the Burgers’ 
 equation,” 2012, vol. 219, pp. 1031–1039.
 [19]. F. F. Peng and X. L. Han, “Parametric splines on a hyperbolic paraboloid,” Journal of 
18 Khoa học & Công nghệ - Số 23/Tháng 9 - 2019 Journal of Science and Technology
 ISSN 2354-0575
 Computational and Applied Mathematics, Jul 1 2009, vol. 229, pp. 183-191.
 [20]. A. Martin and I. D. Boyd, “Variant of the Thomas Algorithm for opposite-bordered tridiagonal 
 systems of equations,” International Journal for Numerical Methods in Biomedical Engineering, Jun 
 2010, vol. 26, pp. 752-759.
 GIẢI BÀI TOÁN TRUYỀN NHIỆT TRONG HÀN SIÊU ÂM
 DỰA TRÊN PHƯƠNG PHÁP SAI PHÂN KẾT HỢP ĐƯỜNG CONG
Tóm tắt:
 Phương pháp sai phân kết hợp đường cong được phát triển để giải bài toán phi tuyến trong hàn 
siêu âm. Phương pháp này có quy trình tính toán đơn giản như phương pháp sai phân hữu hạn. Ngoài ra, 
phương pháp được đề xuất có thể đơn giản hóa độ phức tạp của các biểu thức của phương pháp đường 
cong truyền thống và tăng độ chính xác của các đạo hàm bậc nhất và bậc hai theo không gian từ OxT 2 
 _i
của phương pháp sai phân hữu hạn sang O(Tx 4). Theo sự phân bố nhiệt độ tính toán trong chi tiết hàn 
trong quá trình hàn siêu âm, phương pháp đề xuất đã cho thấy rằng không chỉ độ chính xác của phương 
pháp được nâng cao đáng kể, mà khái niệm của nó cũng rất giống với phương pháp sai phân hữu hạn. Dựa 
trên kết quả phân tích, ta đã kết luận rằng phương pháp sai phân kết hợp đường cong là đơn giản và có độ 
chính xác cao, có tiềm năng tốt để thay thế phương pháp sai phân hữu hạn truyền thống.
Từ khóa: Hàn siêu âm kim loại, phương pháp sai phân kết hợp đường cong, phương pháp sai phân hữu 
hạn.
Khoa học & Công nghệ - Số 23/Tháng 9 - 2019 Journal of Science and Technology 19