Phương pháp toán tử FK cải tiến giải phương trình Schrödinger cho Exciton hai chiều trong từ trường đều

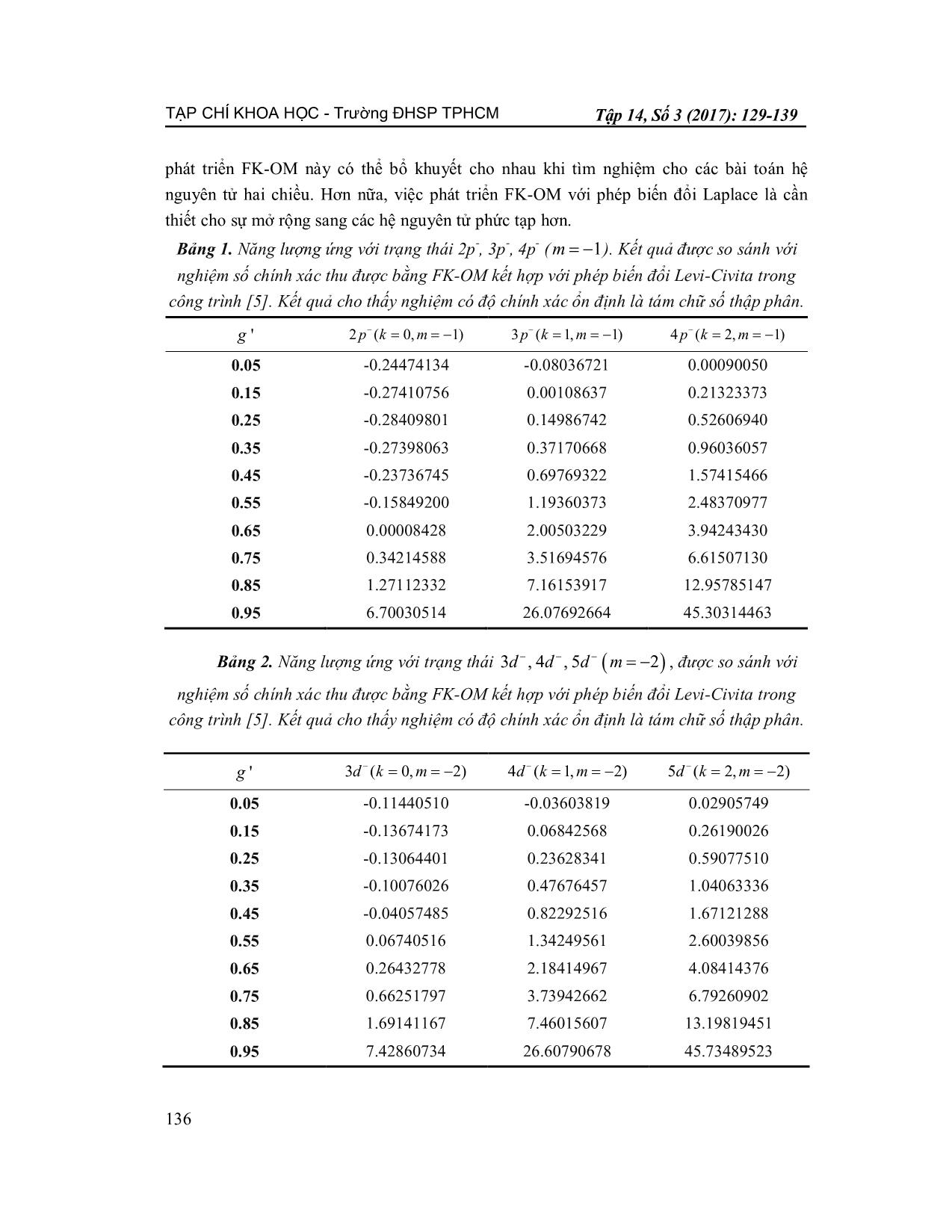
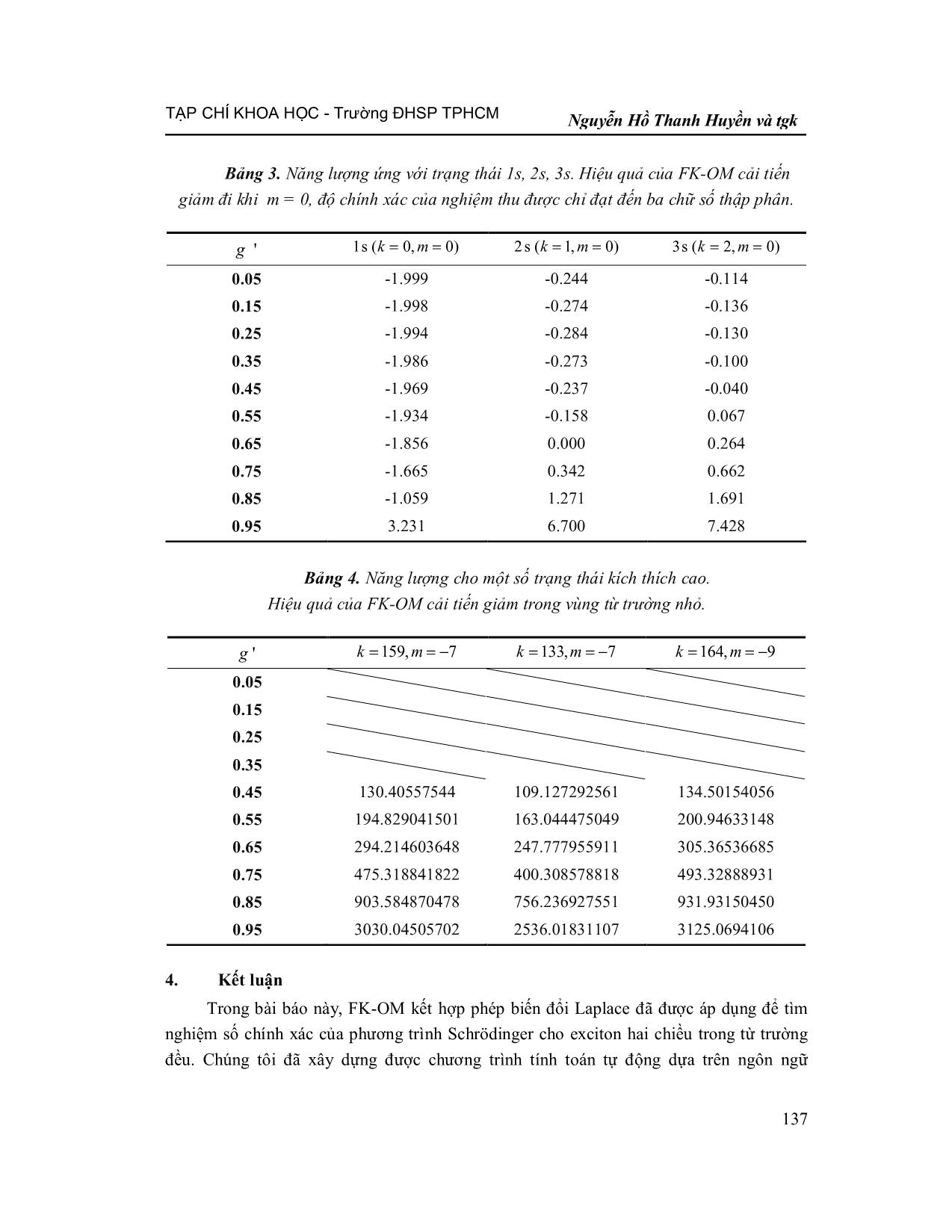
TRƯỜNG ĐẠI HỌC SƯ PHẠM TP HỒ CHÍ MINH 
TẠP CHÍ KHOA HỌC 
HO CHI MINH CITY UNIVERSITY OF EDUCATION
JOURNAL OF SCIENCE
ISSN: 
1859-3100 
KHOA HỌC TỰ NHIÊN VÀ CÔNG NGHỆ 
Tập14, Số 3 (2017): 129-139 
NATURAL SCIENCES AND TECHNOLOGY
Vol. 14, No. 3 (2017): 129-139
 Email: tapchikhoahoc@hcmue.edu.vn; Website:  
129 
PHƯƠNG PHÁP TOÁN TỬ FK CẢI TIẾN 
GIẢI PHƯƠNG TRÌNH SCHRÖDINGER 
CHO EXCITON HAI CHIỀU TRONG TỪ TRƯỜNG ĐỀU 
Nguyễn Hồ Thanh Huyền1, Hoàng Đỗ Ngọc Trầm2* 
1 Trường Đại học Khoa học Tự nhiên – ĐHQG TPHCM 
2 Khoa Vật lí - Trường Đại học Sư phạm TP Hồ Chí Minh 
Ngày Tòa soạn nhận được bài: 16-9-2016; ngày phản biện đánh giá: 10-10-2016; ngày chấp nhận đăng: 24-3-2017 
TÓM TẮT 
Phương pháp toán tử FK với phép biến đổi Laplace được áp dụng để tìm lại nghiệm số cho 
bài toán exciton hai chiều trong từ trường đều nhằm thay thế phép biến đổi Levi-Civita trong vùng 
từ trường lớn và phát triển cho các hệ phức tạp. Kết quả thu được nghiệm số với độ chính xác tám 
chữ số thập phân cho các trạng thái có chỉ số lượng tử đến hàng trăm. Độ chính xác này giảm khi 
từ trường nhỏ và đối với trạng thái có số lượng tử từ 0m . Như vậy, phép biến đổi Laplace 
không thay thế được hoàn toàn cho phép biến đổi Levi-Civita khi xác định nghiệm số, nhưng vẫn 
có ý nghĩa cho phân tích giải tích và thuận lợi để phát triển cho những hệ phức tạp. 
Từ khóa: exciton hai chiều, nghiệm số, phương pháp toán tử, phương trình Schrödinger, từ 
trường. 
ABSTRACT 
The modified FK operator method for solving the Schrödinger equation 
of two-dimensional exciton in a uniform magnetic field of arbitrary strength 
FK Operator Method combined with Laplace transformation is used to retrieve numerical 
solutions of the problem of 2D exciton in a uniform magnetic field (MF) in order to replace the 
Levi-Civita transformation in the case of high MF. Numerical solutions with precision of eight 
decimal places are found for states with quantum number up to hundreds. This presicion decreases 
for states with the magnetic quantum number m=0 and in weak MF. Therefore, the Laplace 
transformation can not be replaced entirely for the Levi-Civita one to get numerical solutions but it 
is meaningful for analytical analysis and for complex systems. 
Keywords: laplacetransformation, numerical solution, operator method, Schrödinger 
equation, two-dimensional exciton. 
* Email: tramhdn@hcmup.edu.vn 
TẠP CHÍ KHOA HỌC - Trường ĐHSP TPHCM Tập 14, Số 3 (2017): 129-139 
130 
1. Mở đầu 
Exciton là trạng thái liên kết giữa điện tử và lỗ trống trong các tinh thể bán dẫn, đây 
là đối tượng nghiên cứu quan trọng trong các nghiên cứu cơ bản và các ứng dụng trong 
quang điện tử [1]. Đặc biệt, trong các hệ bán dẫn hai chiều đang rất được quan tâm như 
TMDs (Transition Metal Dichacogenics), việc hình thành exciton chính là hình thức 
chuyển dời quang học chủ yếu [2]. Việc tìm phổ năng lượng của exciton là một trong các 
hướng nghiên cứu được quan tâm do phổ hấp thụ của exciton có cấu trúc rõ nét, cho phép 
thực hiện các phân tích chi tiết về mặt lí thuyết. Tuy nhiên, năng lượng của các trạng thái 
kích thích của exciton rất khó đo được trong thực nghiệm [3]. Vì vậy, người ta thường sử 
dụng trường ngoài trong các nghiên cứu về đo đạc phổ năng lượng của exciton, đặc biệt là 
từ trường. Đối với các hệ exciton, việc áp dụng từ trường vào hệ sẽ giam hãm exciton, làm 
tăng cường độ dao động và khối lượng hiệu dụng của exciton Do đó, năng lượng liên kết 
của các exciton cũng được tăng lên [4], phổ năng lượng ứng với các trạng thái kích thích 
của các exciton rõ nét hơn. Vì vậy, việc tìm phổ năng lượng của exciton trong từ trường 
giúp ta có thể nghiên cứu và giải thích một số hiệu ứng vật lí cũng như hiểu thêm về các 
tính chất quang của hệ bán dẫn dưới sự tác dụng của từ trường. 
Việc giải phương trình Schrödinger để tìm phổ năng lượng và các hàm riêng của 
exciton hai chiều trong từ trường được nhiều nhóm nghiên cứu quan tâm [5-8]. Phương 
pháp toán tử FK (FK-OM) [9] đã được áp dụng để giải bài toán exciton trong từ trường đều 
với cường độ bất kì bằng cách kết hợp với phép biến đổi Levi-Civita. Kết quả thu được là 
nghiệm số chính xác (hàm sóng và năng lượng) đến 20 chữ số thập phân cho trạng thái cơ 
bản và các trạng thái kích thích với số lượng tử chính lên đến 150, là một kỉ lục trong 
hướng nghiên cứu này [5, 6]. Tuy nhiên, việc kết hợp phép biến đổi Levi-Civita với FK-
OM cũng gặp một số khó khăn khi áp dụng cho bài toán. Thứ nhất, khi sử dụng FK-OM 
kết hợp với phép biến đổi Levi-Civita, bộ hàm sóng cơ sở là bộ hàm riêng của bài toán 
nguyên tử dưới tác dụng của tương tác Coulomb. Bộ hàm sóng này làm việc tốt trong 
trường hợp từ trường nhỏ. Trong trường hợp từ trường lớn, hiệu quả của phương pháp 
giảm đi, thể hiện qua sự giảm tốc độ hội tụ về nghiệm chính xác cũng như sự thu hẹp miền 
hội tụ được theo tham số tự do dùng hiệu chỉnh tốc độ hội tụ. Đồng thời, cũng do bộ hàm 
sóng cơ sở là bộ hàm Coulomb, việc ...  ta chọn các toán tử sinh hủy mới sao cho ˆzL có dạng chéo hóa: 
( )
( ) ( )
1 1ˆ ˆˆ ˆ ˆ ˆ, ( ),
2 2
1 1ˆ ˆˆ ˆ ˆ ˆ, .
2 2
u a ib u a ib
v a ib v a ib
+ + +
+ + +
= + = -
= - = +
 (6) 
Các toán tử này cũng thỏa mãn các hệ thức giao hoán như biểu thức (5): 
ˆ ˆ ˆ ˆ, , 1.u u v v+ +é ù é ù= =ê ú ê úë û ë û (7) 
Khi đó toán tử hình chiếu moment động lượng quỹ đạo được viết lại như sau: 
ˆ ˆ ˆ ˆ .ˆzL u u v v
+ += - (8) 
Lúc này, Hamiltonian trong biểu diễn đại số có dạng như sau: 
( ) ¶ µ ·( )
2
0
2ˆ ˆ ˆ ˆ
4 2 16
m dH M M N M N M Zw g g w t
w p t
+ ¥
+ += - + - + + + + - ò (9) 
( )
( )
( )
( )
( )
( )
2
ˆ ˆ2 /2 /2
0 0 0
1 1 1 1ˆ ˆ ˆ ˆ .
1 2 ! ! 1 2! 1 2 1 2
i i j
i ii j
N N
i i j
i j
M M M M
i ji
t t
t tt t
+¥ ¥ ¥
+ +
= = =
¹
æ ö÷ç ÷æ ö æ öç - - ÷÷ ÷ç ç ç ÷´ +÷ ÷ç ç ç ÷÷ ÷ç çç ÷è ø è ø+ +ç ÷+ + ÷çè ø
å å å
trong đó ˆ ˆˆ ˆ ˆ ˆ ˆ ˆ2 , 2 2 2M u v N u u v v+ + + + += = + + và ˆ ˆ ˆ2M uv= . Các toán tử này cũng tạo 
thành một đại số kín với các hệ thức giao hoán:
 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ, 4 , , 2 , , 4 .M N M M M N N M M+ + +é ù é ù é ù= = =ê ú ê ú ê úë û ë û ë û (10) 
Các biểu thức giao hoán (10) chính là cơ sở cho các tính toán đại số. 
Bước 2. Tách Hamilton thành hai phần: phần chính gồm các toán tử trung hòa (có số 
toán tử sinh và hủy bằng nhau), phần còn lại là nhiễu loạn: 
TẠP CHÍ KHOA HỌC - Trường ĐHSP TPHCM Nguyễn Hồ Thanh Huyền và tgk 
133 
( )
( )
( )
( ) ( )
( )
( )
22
ˆ0 2 /2
00
2
ˆ /2
0 00
2 1 1ˆ ˆ ˆ ˆ ,
4 16 2 1 2! 1 2
2 1 1ˆ ˆ ˆ ˆ ˆ .
4 16 ! ! 1 2 1 2
i
i i
N
i
i j
i j
N
i j
i j
m d
H N Z M M
i
d
V M M Z M M
i j
w g g w t t
w p tt t
w g w t t
w p tt t
+ ¥ ¥
+
=
++¥ ¥ ¥
+ +
= =
¹
-
= + + -
+ +
-
= - + + -
+ +
æ ö æ ö÷ç ÷ç÷ ÷ç ç÷ ÷çç ÷ è øè ø
æ ö æ ö÷ç ÷ç÷ ÷ç ç÷ ÷çç ÷ è øè ø
åò
å åò
 (11) 
Với cách tách như trên, ta thấy cả hai thành phần trên đều phụ thuộc tham số tự do 
w được đưa vào trong Bước 1. Sở dĩ tham số này gọi là tự do vì Hamiltonian toàn phần 
không phụ thuộc giá trị của nó. Do đó, giá trị của tham số w không làm ảnh hưởng đến 
nghiệm chính xác của bài toán. Mặc dù vậy, tham số này có thể hiệu chỉnh tốc độ hội tụ vì 
khi lựa chọn giá trị phù hợp, phần chính của Hamiltonian chiếm ưu thế so với thành phần 
nhiễu loạn – hay nói cách khác là nghiệm gần đúng bậc không sẽ rất gần với kết quả chính 
xác, vì vậy bài toán sẽ hội tụ nhanh. 
Bước 3. Chọn bộ hàm sóng cơ sở là hàm riêng của phần chính và hình chiếu moment 
quỹ đạo lên trục z: 
( )
( ) ( ) ( )1 ˆ ˆ, 0
! !
k m k
k m u v
k k m
w
++ +=
+
khi , (12) 
( )
( ) ( ) ( )1 ˆ ˆ, 0
! !
k k m
k m u v
k k m
w
++ +=
+
khi , (13) 
với 0, 1, 2,...k ; 0, 1, 2,...m là số lượng tử từ (trị riêng của ˆzL ) và trạng thái “chân 
không” ( )0 w được xác định bởi phương trình: 
ˆ ˆ0( ) 0, 0( ) 0, 0( ) 0( ) 1.u vw w w w= = = (14) 
Khi tác dụng các toán tử ˆ ˆ ˆ, ,M N M + lên các hàm sóng cơ sở (12), (13), ta thu được 
kết quả giống nhau: 
( )( )
( )
ˆ , 2 1 1 1, ,
ˆ , 2 ( ) 1, ,
ˆ , 2 2 1 , .
M k m k k m k m
M k m k k m k m
N k m k m k m
+ = + + + +
= + -
= + +
 (15) 
Bước 4. Tìm nghiệm số chính xác của bài toán 
Hàm sóng chính xác dưới dạng tổ hợp tuyến tính của các hàm sóng cơ sở: 
max
,
0
( ) , .
N
k m k
k
x C k m
=
Y = å
(16) 
0m 
0m 
TẠP CHÍ KHOA HỌC - Trường ĐHSP TPHCM Tập 14, Số 3 (2017): 129-139 
134 
Ở đây, ta giả sử hàm sóng hội tụ về nghiệm chính xác khi max .k N= 
Ta thay hàm sóng (16) vào phương trình (1) và thực hiện một số tính toán, ta có 
phương trình Schrödinger dưới dạng ma trận: 
max max
'
1 1
,
N N
k k k k
k k
C H E C
= =
=å å (17) 
hay ( )( ) ( )H C E C= (18) 
với ma trận ( )H có các thành phần k,k'H và ma trận ( )C có các thành phần 1,.., kC C . Các 
trị riêng E là các nghiệm mà ta cần tìm, nghiệm này càng tiến tới giá trị chính xác khi maxN 
càng lớn. Trong đó, các yếu tố ma trận ( )H được xác định bởi: 
( )
( )
( )
( )( )
2
2
, 2 12
0
! !12 2 1 ,
2 16 4 ! !!
k
i
k k k m
i
k k mmH k m Z I
k i k m ii
g g w w
w + +=
æ ö +÷ç ÷= + + + + -ç ÷ç ÷ - + -è ø å 
( )( )
( )
( ) ( )( )
( )( )
2
, 1
1
2 1
2 2
1
2 1 1
16 4
! ! 1 ! 1 !1 ,
! 1 ! 1 ! 1 !
k k
k
i
k m
i
H k k m
k k m k k m
Z I
i i k i k m i
g w
w
w
+
+
-
+ +
=
æ ö÷ç ÷= - + + +ç ÷ç ÷è ø
+ + + +
-
- - + + - +å
 (19) 
( )
( )( )( )
( )( )
2
, 2 1
( 1)
! ! ! !1 ,
! ! ! !
k s
i s
k s k k s m
s i s
k k m k s k s m
H Z I
i i s k i s k m i s
w
+
-
+ + + +
> =
+ + + +
= -
- - + + - +å 
với 
( )
( ) ( )
( )
0
,
2
2
0
1 11
2 2 2 .
(1 )
p q
p q Z
qq
p
q
p
p q qt
dt
t p
I
p p
> ³
Î
+ ¥
æ ö æ ö÷ ÷ç ç- G - - G +÷ ÷ç ç÷ ÷- ç çè ø è ø= =
+ Gò (20) 
3. Kết quả và thảo luận 
Từ các kết quả tính toán, chúng tôi đã xây dựng chương trình tính toán tự động dựa 
trên ngôn ngữ FORTRAN. Trong chương trình có sử dụng gói LAPACK tìm nghiệm cho 
bài toán hàm riêng trị riêng trong thư viện Intel Math Kernel. Kết quả thu được nghiệm số 
cho các trạng thái ứng với các số lượng tử k lên đến hàng trăm và số lượng tử từ 0m ¹ 
với độ chính xác ổn định khoảng tám chữ số thập phân khi kết quả viết dưới dạng chuẩn. 
Để minh họa, trong các Bảng 1-4, chúng tôi trình bày kết quả cho một số trạng thái có thể 
so sánh được với các kết quả trong công trình [5] và một số kết quả mở rộng khác. Để dễ 
so sánh, ở đây cường độ từ trường được thể hiện qua đại lượng ' / ( 1)g g g= + . Năng 
lượng của các trạng thái có m dương có thể được suy ra từ các trạng thái có m âm dựa vào 
TẠP CHÍ KHOA HỌC - Trường ĐHSP TPHCM Nguyễn Hồ Thanh Huyền và tgk 
135 
mối quan hệ: , , .k m k mE E mg-= + Kết quả cho thấy FK-OM cải tiến cho phép thu được 
nghiệm số cho bài toán. Kết quả này không có độ chính xác cao như trong công trình [5] 
khi sử dụng phép biến đổi Levi-Civita (20 chữ số thập phân). Một trong những lí do là do 
trong công trình [5], chương trình tính toán sử dụng gói hỗ trợ cho phép các dữ liệu đạt đến 
độ chính xác là 50 chữ số thập phân, trong công trình này, do mặc định của gói LAPACK, 
các dữ liệu chỉ đạt đến độ chính xác tối đa là 15 chữ số thập phân. Việc phát triển bộ code 
để thu được kết quả chính xác hơn cần được nghiên cứu tiếp. Tuy nhiên, những kết quả đã 
đạt được vẫn đủ cho các phân tích giải tích để tìm hiểu bản chất hệ vật lí. 
Mặt khác, từ các số liệu thu được, ta có thể thấy FK-OM cải tiến không hiệu quả cho 
miền từ trường nhỏ. Trong quá trình chạy chương trình tìm các năng lượng chính xác cho 
các trạng thái 0, 4k m tới 168, 9,k m chúng tôi thấy rằng với các trường hợp từ 
trường mạnh ( ' cỡ 0.65 trở lên) thì vùng lựa chọn tham số tự do để nghiệm hội tụ về 
nghiệm chính xác rộng hơn so với vùng lựa chọn tham số tự do trong vùng từ trường yếu (
' cỡ 0.35 trở xuống). Cụ thể, đối với trạng thái có 8, 9:k m trong từ trường yếu 
' 0.15 có vùng lựa chọn tham số  để có nghiệm chính xác 10 chữ số thập phân nằm 
trong khoảng (0.25, 0.50); trong từ trường mạnh ' 0.85 có vùng lựa chọn tham số  để 
nghiệm chính xác 10 chữ số thập phân nằm trong khoảng (1.25, 6.00). Điều này là phù hợp 
với dự đoán ban đầu, vùng lựa chọn tham số  để nghiệm hội tụ chính xác sẽ rộng hơn 
trong vùng từ trường mạnh. Điều này có thể giải thích là do khi kết hợp phép biến đổi 
Laplace vào phương pháp toán tử FK để tìm năng lượng chính xác, phần tương tác từ 
trường là phần chính và phần tương tác Coulomb là phần nhiễu loạn. Mặt khác, từ Bảng 4, 
ta thấy rất khó có thể xác định được các giá trị năng lượng của các trạng thái kích thích cao 
trong vùng từ trường yếu. Trong vùng từ trường yếu ( ' 0.05 tới ' 0.35 ), ta không tìm 
được giá trị của tham số  để xác định nghiệm số chính xác của một số trạng thái kích 
thích cao. Từ đó, ta có thể kết luận là trong vùng từ trường mạnh, FK-OM kết hợp với 
phép biến đổi Laplace tìm năng lượng chính xác có phần dễ dàng hơn so với trong vùng từ 
trường yếu. 
Ngoài ra, trong Bảng 3 ta cũng có thể thấy rằng độ chính xác của các kết quả ứng với 
các trạng thái có số số lượng tử từ 0m= bị giảm còn ba chữ số thập phân. Điều này có thể 
giải thích rằng đối với trường hợp 0m= , đóng góp của từ trường trong phần chính của 
Hamiltonian bị giảm đi đáng kể, dẫn đến việc hội tụ chậm. 
Như vậy có thể nói, việc kết hợp phép biến đổi Laplace trong FK-OM không thể thay 
thế được hoàn toàn được phép biến đổi Levi-Civita trong việc tìm nghiệm số chính xác. 
Tuy nhiên, với khả năng áp dụng của FK-OM cải tiến trong vùng từ trường lớn, hai hướng 
TẠP CHÍ KHOA HỌC - Trường ĐHSP TPHCM Tập 14, Số 3 (2017): 129-139 
136 
phát triển FK-OM này có thể bổ khuyết cho nhau khi tìm nghiệm cho các bài toán hệ 
nguyên tử hai chiều. Hơn nữa, việc phát triển FK-OM với phép biến đổi Laplace là cần 
thiết cho sự mở rộng sang các hệ nguyên tử phức tạp hơn. 
Bảng 1. Năng lượng ứng với trạng thái 2p-, 3p-, 4p- ( 1m ). Kết quả được so sánh với 
nghiệm số chính xác thu được bằng FK-OM kết hợp với phép biến đổi Levi-Civita trong 
công trình [5]. Kết quả cho thấy nghiệm có độ chính xác ổn định là tám chữ số thập phân. 
2 ( 0, 1)p k m 3 ( 1, 1)p k m 4 ( 2, 1)p k m 
0.05 -0.24474134 -0.08036721 0.00090050 
0.15 -0.27410756 0.00108637 0.21323373 
0.25 -0.28409801 0.14986742 0.52606940 
0.35 -0.27398063 0.37170668 0.96036057 
0.45 -0.23736745 0.69769322 1.57415466 
0.55 -0.15849200 1.19360373 2.48370977 
0.65 0.00008428 2.00503229 3.94243430 
0.75 0.34214588 3.51694576 6.61507130 
0.85 1.27112332 7.16153917 12.95785147 
0.95 6.70030514 26.07692664 45.30314463 
Bảng 2. Năng lượng ứng với trạng thái 3 , 4 , 5 2d d d m , được so sánh với 
nghiệm số chính xác thu được bằng FK-OM kết hợp với phép biến đổi Levi-Civita trong 
công trình [5]. Kết quả cho thấy nghiệm có độ chính xác ổn định là tám chữ số thập phân. 
3 ( 0, 2)d k m 4 ( 1, 2)d k m 5 ( 2, 2)d k m 
0.05 -0.11440510 -0.03603819 0.02905749 
0.15 -0.13674173 0.06842568 0.26190026 
0.25 -0.13064401 0.23628341 0.59077510 
0.35 -0.10076026 0.47676457 1.04063336 
0.45 -0.04057485 0.82292516 1.67121288 
0.55 0.06740516 1.34249561 2.60039856 
0.65 0.26432778 2.18414967 4.08414376 
0.75 0.66251797 3.73942662 6.79260902 
0.85 1.69141167 7.46015607 13.19819451 
0.95 7.42860734 26.60790678 45.73489523 
'g
'g
TẠP CHÍ KHOA HỌC - Trường ĐHSP TPHCM Nguyễn Hồ Thanh Huyền và tgk 
137 
Bảng 3. Năng lượng ứng với trạng thái 1s, 2s, 3s. Hiệu quả của FK-OM cải tiến 
giảm đi khi m = 0, độ chính xác của nghiệm thu được chỉ đạt đến ba chữ số thập phân. 
1s ( 0, 0)k m 2s ( 1, 0)k m 3s ( 2, 0)k m 
0.05 -1.999 -0.244 -0.114 
0.15 -1.998 -0.274 -0.136 
0.25 -1.994 -0.284 -0.130 
0.35 -1.986 -0.273 -0.100 
0.45 -1.969 -0.237 -0.040 
0.55 -1.934 -0.158 0.067 
0.65 -1.856 0.000 0.264 
0.75 -1.665 0.342 0.662 
0.85 -1.059 1.271 1.691 
0.95 3.231 6.700 7.428 
Bảng 4. Năng lượng cho một số trạng thái kích thích cao. 
Hiệu quả của FK-OM cải tiến giảm trong vùng từ trường nhỏ. 
159, 7k m 133, 7k m 164, 9k m 
0.05 
0.15 
0.25 
0.35 
0.45 130.40557544 109.127292561 134.50154056 
0.55 194.829041501 163.044475049 200.94633148 
0.65 294.214603648 247.777955911 305.36536685 
0.75 475.318841822 400.308578818 493.32888931 
0.85 903.584870478 756.236927551 931.93150450 
0.95 3030.04505702 2536.01831107 3125.0694106 
4. Kết luận 
Trong bài báo này, FK-OM kết hợp phép biến đổi Laplace đã được áp dụng để tìm 
nghiệm số chính xác của phương trình Schrödinger cho exciton hai chiều trong từ trường 
đều. Chúng tôi đã xây dựng được chương trình tính toán tự động dựa trên ngôn ngữ 
'g
'g
TẠP CHÍ KHOA HỌC - Trường ĐHSP TPHCM Tập 14, Số 3 (2017): 129-139 
138 
FORTRAN cho phép xác định năng lượng của các trạng thái với các chỉ số lượng tử lên 
đến hàng trăm. Đối với trạng thái ứng với số lượng tử từ , độ chính xác đến tám chữ 
số thập phân. Đối với trạng thái ứng với số lượng tử từ , độ chính xác giảm còn ba 
chữ số thập phân. Thêm vào đó, trong vùng từ trường yếu ta rất khó xác định nghiệm cho 
các trạng thái kích thích cao. Như vậy có thể nói, việc kết hợp phép biến đổi Laplace trong 
FK-OM không thể thay thế được hoàn toàn được phép biến đổi Levi-Civita trong việc tìm 
nghiệm số chính xác. Tuy nhiên, với sự hiệu quả của FK-OM cải tiến trong vùng từ trường 
lớn, hai phép biến đổi có thể được kết hợp với FK-OM để bổ khuyết cho nhau khi tìm 
nghiệm cho các bài toán hệ nguyên tử hai chiều. Hơn nữa, việc phát triển FK-OM với phép 
biến đổi Laplace là cần thiết cho sự phát triển sang các hệ nguyên tử phức tạp hơn. 
Lời cảm ơn: Nghiên cứu này được tài trợ bởi Quỹ Phát triển khoa học và công nghệ Quốc 
gia (NAFOSTED) trong đề tài mã số 103.01-2014.44. 
TÀI LIỆU THAM KHẢO 
[1] Mak K. F. and Shan J., “Photonics and optoelectrics of 2D semiconductor transition metal 
dichalcogenides,” Nature Photonics 10, pp. 216-226, 2016. 
[2] Hao K. et al., “Direct measurement of exciton valley coherence in monolayer WSe2,” Nature 
Phys. 12, pp. 1-7, 2016. 
[3] Miller R. C., Kleinman D. A., Tsang W. T. and Grossard A. C., “Observation of the excited 
level of excitons in GaAs quantum wells,”, Physical Review B 24, 2, pp. 1134-1136, 1981. 
[4] Branis S. V., Cen J. and Bajaj K. K., “Effect of magnetic fields on exciton binding energies 
in type-II GaAs-AlAs quantum-well structures,” Physical Review B 44, 20, pp. 196-202, 
1991. 
[5] Hoang-Do Ngoc-Tram, Pham Dang-Lan and Le Van-Hoang, “Exact numerical solutions of 
the Schrödinger equation for a two-dimensional exciton in a homogeneous magnetic field of 
arbitrary strength,” Physica B 423, pp. 31-37, 2013. 
[6] Hoang D. Ngoc-Tram, Nguyen P. Duy-Anh, Hoang Van-Hung and Le Van-Hoang, “Highly 
accurate analytical energy of a two-dimensional exciton in a constant magnetic field,” 
Physica B 495, pp. 16-20, 2016. 
[7] Pino R. and Villalba V. M., “Scaled variational computation of the energy spectrum of a 
two-dimensional hydrogenic donor in a magnetic field of arbitrary strength,” Revista 
Mexicana de Fisica 47, 2, pp. 24-29, 2001. 
[8] Soylu A. and Boztosun I. (2008), “Asymptotic iteration method solution of the energy 
spectrum of two-dimensional screened donor in a magnetic field,” Physica E 40, 3, pp. 443-
448. 
0m ¹
0m =
TẠP CHÍ KHOA HỌC - Trường ĐHSP TPHCM Nguyễn Hồ Thanh Huyền và tgk 
139 
[9] Feranchuk I. D. and Komaro L. I., “The operator method of the approximate solution of the 
Schrödinger equation,” Physics Letters A 88, 5, pp. 211-214, 1982. 
[10] Lý Duy Nhất, Huỳnh Nguyễn Thanh Trúc, Nguyễn Văn Hoa, Nguyễn Phương Duy Anh và 
Lê Văn Hoàng, “Phương pháp toán tử FK cho bài toán nguyên tử hydro trong từ trường với 
cường độ bất kì,” Tạp chí Khoa học – Trường Đại học Sư phạm TPHCM, 40(74) (Khoa học 
tự nhiên & công nghệ), tr. 56-62, 2012. 
[11] Hoàng Đỗ Ngọc Trầm, Lê Quý Giang, Nguyễn Thị Mận và Lê Văn Hoàng, “Phương pháp 
đại số cho bài toán exciton âm trong bán dẫn hai chiều,” Tạp chí Khoa học – Trường Đại học 
Sư phạm TPHCM ,43(77) (Khoa học tự nhiên & công nghệ), tr. 24-32, 2013.