Phát huy tính tích cực và sáng tạo của học sinh trong môi trường khảo sát toán

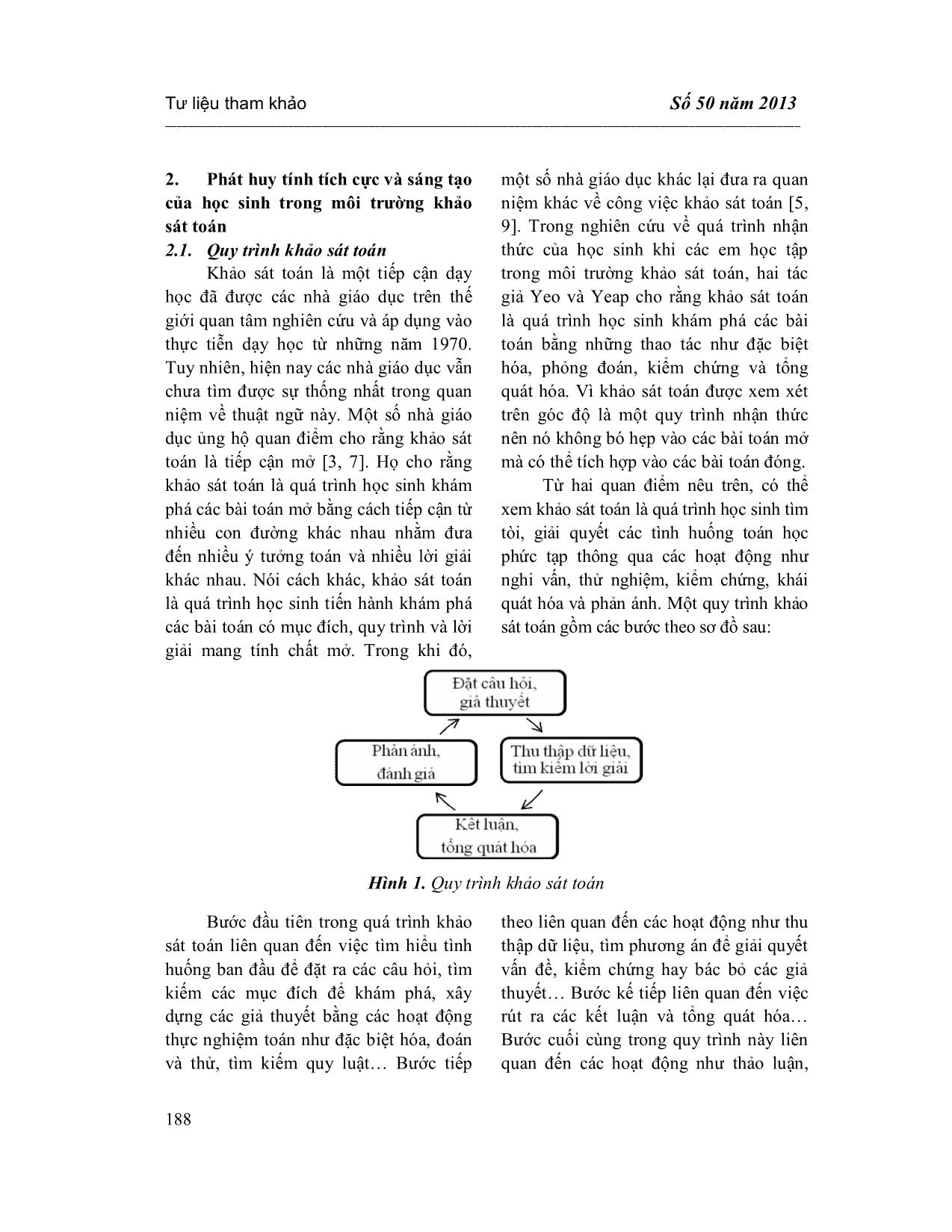
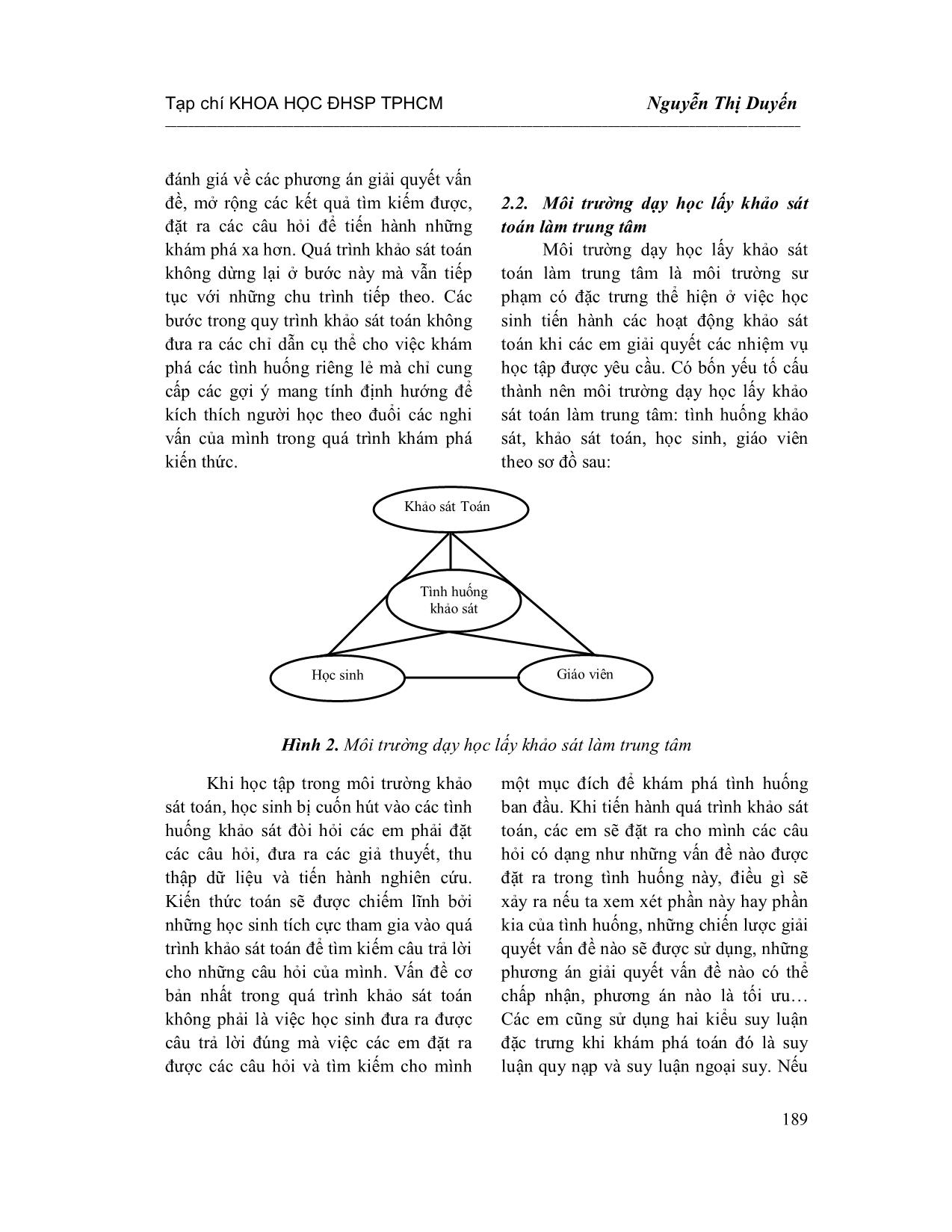
Tư liệu tham khảo Số 50 năm 2013 
_____________________________________________________________________________________________________________ 
 186
PHÁT HUY TÍNH TÍCH CỰC VÀ SÁNG TẠO CỦA HỌC SINH 
TRONG MÔI TRƯỜNG KHẢO SÁT TOÁN 
NGUYỄN THỊ DUYẾN* 
TÓM TẮT 
Khảo sát toán là một tiếp cận dạy học lấy học sinh làm trung tâm. Tiếp cận này đã 
và đang được nghiên cứu và áp dụng trong các thực hành dạy học để đổi mới việc học 
toán của học sinh. Bài viết này trình bày tác động của tiếp cận khảo sát toán đến tính tích 
cực và sáng tạo của học sinh trong quá trình học toán của các em dựa trên một nghiên cứu 
định tính về tiếp cận này. 
Từ khóa: khảo sát toán, quy trình khảo sát toán, môi trường khảo sát toán. 
ABSTRACT 
Promoting students’ being active and creative 
in mathematical investigation environment 
Mathematical investigation is a student-centered teaching approach. This approach 
has been being studied and applied to teaching practices to innovate students' mathematics 
learning. This paper presents the impact of mathematical investigation approach on 
students’ being active and creative during their mathematical learning process from a 
qualitative research on this approach. 
Keywords: Mathematical investigation, mathematical investigation process, 
mathematical investigation environment 
1. Mở đầu 
Phát huy tính tích cực và sáng tạo 
của học sinh trong quá trình học toán là 
một trong những yêu cầu cấp thiết của 
nền giáo dục nước ta trong giai đoạn hiện 
nay nhằm đáp ứng yêu cầu đổi mới việc 
dạy học toán trong nhà trường phổ thông 
và theo kịp xu hướng tiến bộ trong giáo 
dục toán trên thế giới. Mặc dù chương 
trình toán đã được đổi mới hướng đến 
việc phát triển tư duy toán học cho học 
sinh, tuy nhiên việc học toán của một bộ 
phận các em học sinh vẫn chưa đảm bảo 
được yếu tố tích cực và sáng tạo [2]. 
Nghiên cứu của tác giả này chỉ ra rằng 
hầu hết học sinh, kể cả các học sinh có 
* ThS, Trường Đại học Sư phạm Huế 
năng khiếu toán chỉ được giao những bài 
toán mang tính quy trình là chủ yếu. Các 
em ít có cơ hội khám phá những bài toán 
mang tính thách thức, yêu cầu khả năng 
giải quyết các vấn đề thực tiễn và các loại 
hình tư duy bậc cao. Vì thế hầu hết học 
sinh ít có hứng thú với các giờ học toán 
của mình. Trong lúc đó, nhiều nghiên 
cứu đã chỉ ra rằng học sinh thật sự bị 
cuốn hút vào một giờ học toán nếu các 
em được học toán trong một môi trường 
chứa đựng nhiều yếu tố thách thức và 
kích thích trí tò mò, tưởng tượng của các 
em [4]. Nhiều tiếp cận dạy học đã được 
đề xuất để tìm kiếm các môi trường học 
tập tương tác nhằm thúc đẩy việc học 
toán của học sinh như: tiếp cận hỏi-tìm, 
giải quyết vấn đề, khảo sát toán Trong 
Tạp chí KHOA HỌC ĐHSP TPHCM Nguyễn Thị Duyến 
_____________________________________________________________________________________________________________ 
 187 
đó, khảo sát toán được xem là tiếp cận 
dạy học có thể mang lại nhiều cơ hội cho 
học sinh học toán một cách tích cực và 
sáng tạo. Tiếp cận dạy học này đã và 
đang thu hút sự quan tâm, nghiên cứu của 
các nhà giáo dục trên thế giới nhằm tìm 
kiếm cách thức để cải tiến việc học toán 
của học sinh và phát triển năng lực toán 
học cho các em. Tuy nhiên, ở nước ta 
tiếp cận này vẫn chưa được quan tâm 
nghiên cứu và áp dụng một cách rộng rãi 
vào thực tiễn dạy học ở trường phổ 
thông. Vì thế, cần tiến hành nhiều nghiên 
cứu hướng đến việc tìm hiểu tác động của 
tiếp cận khảo sát toán lên quá trình học 
toán của học sinh nhằm phát huy tính tích 
cực và sáng tạo của các em trong quá 
trình học toán. 
Phương pháp nghiên cứu chính 
được sử dụng trong nghiên cứu này là 
phương pháp định tính. Hai hoạt động 
chính trong nghiên cứu này là quan sát 
học sinh khi các em học tập trong môi 
trường khảo sát toán và phỏng vấn các 
em trước và sau các tiết học đó. Thành 
phần tham gia vào nghiên cứu này gồm 
các học sinh của những lớp chọn ban tự 
nhiên 11 1A ,11 3A và 12 1A ở một trường 
trung học phổ thông vùng ngoại ô thành 
phố Huế. Công cụ của nghiên cứu này là 
các tình huống khảo sát toán và bảng câu 
hỏi phỏng vấn học sinh. Để thu thập dữ 
liệu cho nghiên cứu này, các cuộc phỏng 
vấn ban đầu sẽ được thực hiện nhằm tìm 
hiểu về môi trường học toán hàng ngày 
của học sinh. Tiếp đến, các quan sát và 
ghi chú về các chủ điểm dự định thúc đẩy 
tính tích cực và sáng tạo của học sinh sẽ 
được thực hiện khi các em làm việc trong 
môi trường khảo sát toán. Sau đó, các 
cuộc phỏng vấn học sinh sẽ được tiến 
hành nhằm tìm hiểu tác động của môi 
trường khảo sát toán lên việc học toán 
của các em. Dữ liệu thu được từ nghiên 
cứu này sẽ được phân tích một cách định 
tính. Giai đoạn đầu tiên trong quá trình 
phân tích dữ liệu liên quan đến việc viết 
ra các ghi nhớ từ việc xem lại các băng 
ghi hình và ghi âm cũng như đọc lại các 
ghi chú được thực hiện khi quan sát và 
phỏng vấn học sinh. Những ghi nhớ này 
là các mô tả tóm  ... _________________________________________________________________________________________________________ 
 195 
hình hình học biểu diễn tổng 
2 2 2
2S 1 2 n .  Các em đã sử dụng mối 
liên hệ giữa các biểu diễn hình học đó để 
dự đoán kết quả của 2S khi nhận thấy 
 23S 1 2 n 2n 1  nên 
2
n n 1 2n 1
S .
6
Sau đó các em dùng phép chứng minh quy 
nạp để kiểm chứng dự đoán của mình. 
Một số học sinh còn tiến hành những 
khám phá xa hơn khi cố gắng tìm kiếm 
phương pháp tính trực tiếp 2S . Các số 
hạng 2 2 21 , 2 ,..., n trong tổng này làm các em 
liên tưởng đến việc sử dụng các hằng đẳng 
thức dạng 21 x với x 0, 1, 2,...,n. Tuy 
nhiên khi các em cộng các hằng đẳng thức 
vế theo vế thì các số hạng 2 2 21 , 2 ,..., n bị 
triệt tiêu nhưng lại tìm ra tổng 
1S 1 2 n.  Điều đó làm cho các em 
nghĩ đến việc dùng các hằng đẳng thức 
dạng tương tự nhưng bậc phải cao hơn 1 
đơn vị là 31 x . Các em thay x 0, 1, 2,...,n 
vào hằng đẳng thức dạng 31 x : 
Một số học sinh không dừng lại ở 
việc tìm ra tổng 2S , bằng cách tương tự 
các em cho rằng có thể dùng các hằng 
đẳng thức dạng 41 x để tính tổng 
3 3 3
3S 1 2 n .  Rõ ràng, dự đoán của 
các em là chính xác. Có thể thấy môi 
trường khảo sát toán đã mang đến cho 
học sinh nhiều cơ hội để khám phá kiến 
thức toán. Các em không bị gò bó vào 
các phương pháp giải quyết các bài toán 
được trình bày trong sách giáo khoa mà 
cố gắng tìm kiếm các con đường tiếp cận 
khác cho riêng mình. Các em tự do đề 
xuất các giả thuyết và theo đuổi các ý 
tưởng để tìm kiếm cho mình những kết 
quả mới và thú vị bằng cách tiến hành 
các hoạt động ngoại suy, quy nạp, tương 
tự, tìm kiếm quy luật và tổng quát hóa. 
Bên cạnh đó, việc khám phá các tình 
huống khảo sát mở còn mang đến cơ hội 
cho học sinh tìm ra các phương án giải 
quyết vấn đề phù hợp với khả năng của 
bản thân mình. Có thể thấy rõ điều này 
qua việc phân tích đáp ứng của học sinh 
với tình huống tài khoản tiết kiệm. 
Tư liệu tham khảo Số 50 năm 2013 
_____________________________________________________________________________________________________________ 
 196
Tình huống 2 (tài khoản tiết kiệm). 
Một khách hàng muốn gửi tiết kiệm tại 
ngân hàng với số tiền 1.000.000đ. Có hai 
phương án để khách hàng đó lựa chọn, 
phương án thứ nhất là có thể nhận lãi 
suất 7%/năm hoặc phương án thứ hai là 
nhận ngay một phần thưởng 10.000đ của 
ngân hàng và lãi suất 6%/năm. Bạn có 
thể tư vấn cho hành khách đó nên chọn 
gói kí gửi nào? 
Tình huống này được thiết kế để 
dạy phần công thức lãi kép trong bài Lũy 
thừa với số mũ thực, chương Hàm số lũy 
thừa, hàm số mũ và hàm số logarit, Giải 
tích 12 Nâng cao. Đây được xem là một 
tình huống đích thực với bối cảnh xã hội 
gắn liền với kinh nghiệm hàng ngày của 
học sinh đòi hỏi phải các em phải sử 
dụng kiến thức toán để khám phá. Một số 
học sinh cho rằng khách hàng đó chọn 
phương án nào trong hai phương án được 
đưa ra thì lãi suất sau một năm cũng 
giống nhau. Nếu chọn phương án thứ 
nhất thì sau một năm khách hàng đó nhận 
được số tiền lãi là 7%x1.000.000 70.000 đ 
còn nếu chọn phương án thứ hai thì sau 
một năm khách hàng cũng nhận được số 
tiền lãi là 10.000 6%x1000.000 70.000 đ. 
Tuy nhiên một số học sinh lại có ý kiến 
khác. Các em cho rằng nếu gửi trong 
vòng một năm thì phương án thứ hai sẽ 
mang về tiền lãi nhiều hơn bằng cách 
đem 10.000đ tiền thưởng gửi tiếp vào 
ngân hàng. Lúc đó tiền lãi của khách 
hàng sau một năm 
 10.000 6%x 1.000.000 10.000 70.600 đ. 
Một số học sinh lại không đồng ý với ý 
kiến trên, các em cho rằng nếu đem 
10.000đ tiền thưởng gửi tiếp vào ngân 
hàng nhưng theo phương án thứ nhất thì 
sẽ có thêm tiền lãi là 7%x10.000 700 đ và 
khách hàng sẽ nhận được số tiền lãi trong 
một năm là 
10.000 6%x1.000.000 7%x10.000 70.700 đ
Một số học sinh khác còn tiến hành 
những khảo sát xa hơn khi tìm kiếm 
phương án tối ưu cho khách hàng đó với 
kì hạn từ 2 năm trở lên. Các em cho rằng 
nếu gởi từ hai năm trở lên thì phương án 
thứ hai sẽ mang về cho khách hàng đó số 
tiền lãi nhiều hơn. Các em lí giải ý kiến 
của mình như sau: 
Phương án 1: nx 1 0,07 . 
Phương án 2: nx 10.000 1 0,06 
với x là số tiền gốc, n là số năm gửi. 
Xét tỉ số 
n
n
n
x 1 0,07
A
x 10.000 1 0,06
100 107 1 n 1, n .
101 106
¥
Với n 1 thì A 1 nên chọn phương 
án 2. 
Với n 2 thì A 1 nên chọn 
phương án 1. 
Có thể thấy học sinh đã đưa ra 
nhiều ý tưởng khác nhau khi khám phá 
tình huống thực tế trong môi trường khảo 
sát toán. Điều đó thể hiện mức độ phân kì 
trong tư duy của học sinh khi các em 
được tự do trao đổi và tranh luận các ý 
tưởng toán học của mình với bạn học. 
Khi học sinh làm việc với những tình 
huống mở và đòi hỏi phải đưa ra nhiều sự 
lựa chọn thì tư duy của các em hướng 
đến việc tìm ra phương án tối ưu để giải 
Tạp chí KHOA HỌC ĐHSP TPHCM Nguyễn Thị Duyến 
_____________________________________________________________________________________________________________ 
 197 
quyết vấn đề. Bên cạnh đó việc tiến hành 
các hoạt động khảo sát toán trên các tình 
huống mở còn mang đến nhiều cơ hội để 
học sinh đặt ra các vấn đề mới để tự mình 
khám phá. Tùy theo trí tưởng tượng và 
khả năng sáng tạo của mình mà các em 
có thể đặt ra cho mình các vấn đề phù 
hợp để khám phá tình huống ban đầu. 
Các em không chỉ tìm ra nhiều con 
đường khác nhau để giải quyết vấn đề mà 
còn sáng tạo ra các bài toán phù hợp với 
khả năng của mình để theo đuổi. Có thể 
thấy rõ điều này qua việc phân tích đáp ứng 
của học sinh đối với tình huống thủy triều. 
Tình huống 3 (thủy triều). Thuyền 
trưởng của các tàu chở hàng thường phải 
chú ý đến thủy triều khi muốn cho tàu 
cập một bến cảng nào đó vì mực nước 
triều tại cảng đó có thể thay đổi rất lớn 
từ thời điểm này đến thời điểm khác 
trong một ngày. Giả sử rằng chế độ thủy 
triều tại cảng Chân Mây là bán nhật triều 
với đỉnh triều xảy ra lúc 5h và 17h, mực 
nước triều lúc đó là 10m và chân triều 
xảy ra lúc 11h và 23h, mực nước triều 
lúc đó là 6m. Hãy vẽ một đồ thị mà nó có 
thể dự báo mực nước triều tại cảng Chân 
Mây kể từ lúc 0h. 
Tình huống này được thiết kế để 
dạy tiết tự chọn trong chương Ứng dụng 
đạo hàm để khảo sát và vẽ đồ thị của hàm 
số, Giải tích 12 Nâng cao. Hầu hết các 
bài toán về khảo sát và vẽ đồ thị của hàm 
số đều bắt đầu bằng việc cho một hàm số 
và yêu cầu học sinh khảo sát và vẽ đồ thị 
của hàm số đó. Tình huống này mang đến 
cho học sinh một trải nghiệm khác về các 
bài toán vẽ đồ thị của hàm số bằng cách 
sử dụng những số liệu của bài toán để mô 
phỏng đồ thị và sau đó là tìm hàm số 
tương ứng. 
Đây là một tình huống mở về phía 
giả thiết đòi hỏi người học phải thêm 
giả thiết vào để khảo sát. Tùy theo khả 
năng sáng tạo của bản thân mà mỗi học 
sinh có thể chọn cho mình một mục đích 
để khám phá. Vận dụng kiến thức được 
học từ môn Vật lí, hầu hết học sinh cho 
rằng mực nước triều tại bến cảng này 
dao động theo dạng sóng. Bên cạnh đó, 
kiến thức về dao động sóng mà các em 
đã được biết là dao động điều hòa nên 
các em thêm vào giả thiết là “dao động 
của mực nước triều là dao động điều 
hòa” để khám phá tình huống này. Các 
em đều hình dung được mực nước triều 
dao động theo dạng đồ thị một hàm sin 
hoặc hàm cosin. Từ đó các em đưa ra 
được một đồ thị mà có thể dự báo được 
mức nước triều tại cảng này. Một số học 
sinh cho rằng dao động của mực nước 
triều không nhất thiết là một dao động 
điều hòa mà nó có thể là một dao động 
hỗn hợp. Các em đưa ra đồ thị có thể 
mô tả mực nước triều theo dạng dao 
động hỗn hợp tại cảng này. Có thể thấy 
mức độ phân kì trong tư duy của học 
sinh khi các em khảo sát các tình huống 
mở: 
Tư liệu tham khảo Số 50 năm 2013 
_____________________________________________________________________________________________________________ 
 198
Dao động điều hòa Dao động hỗn hợp 
Học sinh còn tiến hành những hoạt 
động khảo sát xa hơn khi tìm kiếm hàm 
số tương ứng với đồ thị trên trong trường 
hợp dao động của mực nước triều là một 
dao động điều hòa bằng cách viết phương 
trình của một dao động sóng 
 f t 2sin t 8
6 3
 hoặc 5f t 2cos t 8.
6 6
Còn với trường hợp dao động hỗn hợp thì 
các em chưa tìm ra được hàm số tương 
ứng với nó. Điều đó cũng có thể lí giải 
được vì để tìm ra một phương trình cho 
một dao động hỗn hợp đòi hỏi thêm kiến 
thức toán cao cấp vượt ra khỏi hiểu biết 
của các em học sinh ở bậc trung học phổ 
thông. 
 Có thể thấy học sinh đã vận dụng 
một cách linh hoạt kiến thức và kĩ năng 
liên môn khi khám phá tình huống này. 
Các em đã vận dụng một cách linh hoạt 
hiểu biết của mình để giải quyết các tình 
huống thực tế. Các em đã biết chuyển từ 
tình huống thực tế thành một bài toán và 
tìm kiếm phương hướng giải quyết bài 
toán đó rồi lí giải kết quả của bài toán đó 
theo tình huống thực tế. Việc khám phá 
các tình huống thực tế trong môi trường 
khảo sát toán đã mang đến nhiều cơ hội 
để học sinh phát huy năng lực mô hình 
hóa. Ngoài ra những tình huống khảo sát 
mở còn tạo điều kiện cho các em phát 
huy trí tưởng tượng và sáng tạo của bản 
thân mình. Chuẩn bị cho học sinh thành 
công với những tình huống này là chuẩn 
bị cho các em năng lực giải quyết vấn đề 
để thành công trong cuộc sống hàng ngày 
của các em sau này. 
Kết quả từ việc phân tích đáp ứng 
của học sinh trong môi trường khảo sát 
toán và phỏng vấn các em sau các tiết 
học đó cho thấy tính tích cực nhận thức 
trong quá trình khảo sát toán của các em 
thể hiện ở nhiều phương diện khác nhau: 
- Hứng khởi và thích thú khi khám 
phá các tình huống chứa đựng những yếu 
tố kích thích và mang tính thách thức. 
- Tập trung và kiên trì theo đuổi các 
ý tưởng của mình trong quá trình khảo 
sát toán. 
- Thoải mái giao tiếp các ý tưởng 
toán với bạn học. 
- Tự mình tìm kiếm và đặt ra các câu 
hỏi để tiến hành các khảo sát xa hơn 
Tính sáng tạo trong quá trình khảo sát 
toán của học sinh cũng được biểu hiện ở 
nhiều khía cạnh khác nhau: 
- Đặt ra được nhiều câu hỏi và nhiều 
vấn đề để khám phá tình huống ban đầu 
đặc biệt là trong các tình huống mở. 
- Đưa ra được nhiều giả thuyết bằng 
các hoạt động thực nghiệm toán, suy luận 
quy nạp và suy luận ngoại suy. 
Tạp chí KHOA HỌC ĐHSP TPHCM Nguyễn Thị Duyến 
_____________________________________________________________________________________________________________ 
 199 
- Tìm kiếm quy luật bằng hoạt động 
đặc biệt hóa, đoán-thử và khái quát hóa. 
- Mở rộng tình huống ban đầu và tìm 
kiếm phương thức giải quyết vấn đề qua 
hoạt động tương tự. 
- Tìm kiếm được nhiều phương án 
giải quyết vấn đề, nhiều lời giải khác 
nhau khi khám phá các tình huống mở 
3. Kết luận 
Nhiều học sinh có cảm giác sợ môn 
toán và thụ động khi học môn học này là 
do việc dạy học toán trong nhà trường 
phổ thông thường chú trọng nhiều đến 
việc đưa ra được các câu trả lời đúng. 
Trong khi đó, khảo sát toán là một tiếp 
cận dạy học mang đến cho học sinh nhiều 
cơ hội khám phá kiến thức toán trong 
một môi trường học tập thú vị và mang 
tính tương tác cao. Ở đó, học sinh được 
tự do theo đuổi các ý tưởng phù hợp với 
mức độ nhận thức của chính mình mà 
không bị ràng buộc bởi việc phải đưa ra 
được những câu trả lời đúng. Các em có 
nhiều cơ hội giao tiếp các ý tưởng toán 
một cách thoải mái với bạn học. Điều này 
mang đến cho học sinh một tâm thế hứng 
khởi khi bước vào các giờ học toán. Đây 
được xem là yếu tố cơ bản để thúc đẩy 
tính tích cực nhận thức trong quá trình 
học toán của các em. Bên cạnh đó, việc 
học sinh được khuyến khích khám phá 
kiến thức thông qua quá trình thực 
nghiệm toán bằng các hoạt động quan sát, 
đoán và thử, đặc biệt hóa, tìm kiếm quy 
luật, tương tự, khái quát hóa trong quá 
trình khảo sát toán đã mang đến nhiều cơ 
hội để các em phát huy năng lực sáng tạo 
của bản thân mình. Những hoạt động 
khảo sát toán với các tình huống thực tế 
mà học sinh cần mô phỏng để hiểu và sử 
dụng chúng cũng tạo ra môi trường để 
học sinh phát huy năng lực mô hình hóa 
toán học của mình. Vì thế, các giáo viên 
toán cần tích hợp tiếp cận khảo sát toán 
vào việc dạy học của mình để đổi mới 
việc học toán của học sinh trong nhà 
trường phổ thông hướng đến phát huy 
năng lực hiểu biết toán và sử dụng toán 
để giải quyết các vấn đề thực tiễn nhằm 
chuẩn bị cho các em thành công trong 
cuộc sống sau này. 
TÀI LIỆU THAM KHẢO 
1. Trương Thị Khánh Phương (2011), “Sử dụng biểu diễn trực quan động hỗ trợ suy 
luận quy nạp và ngoại suy của học sinh trong quá trình khám phá toán học”, Tạp chí 
Khoa học Trường Đại học Sư phạm Hà Nội, 56(5), tr. 109-116. 
2. Trần Vui (2010), “A combined abduction-induction strategy in teaching mathematics 
to gifted students-with-computers through dynamic representations”, Proceedings of 
APEC Conference on Replicating Exemplary Practices in Mathematics Education, 
pp. 1-10, Samui, Thailand. 
3. Bailey, J. (2007), “Mathematical investiagations: A primary teacher educator’s 
narrative journey of professional awareness", Proceedings of the 30th annual 
conference of the Mathematics Education Research Group of Australasia, 
Mathematics: Essential research, essential practice, Vol.1, pp. 103-112, Adelaide. 
Tư liệu tham khảo Số 50 năm 2013 
_____________________________________________________________________________________________________________ 
 200
4. Flewelling, G. & Higginson, W. (2002), Teaching with rich learning tasks: A 
handbook, Australian Association of Mathematics Teachers, Adelaide. 
5. Jaworski, B. (1994), Investigating mathematics learning: A constructivist enquiry, 
Falmer Press, London. 
6. Ponte, J. P., Ferreira, C., Brunheira, L., Oliveira, H., & Varandas, J. M. (1998), 
“Investigating mathematical investigations”, Proceedings of the CIEAEM 49: Les 
interactions dans la classe de mathématiques, pp. 3-14, Setúbal: ESE de Setúbal. 
7. Quinnell, L. (2010), “Why are Mathematical Investigations important?”, Australian 
Mathematics Teacher, Vol. 66, No.3, pp. 35-40. 
8. Sullivan, P. & Lilburn, P. (2002), Good Questions for Math Teaching: Why Ask 
Them and What to Ask [K-6], Math Solutions Publications, Sausalito, CA. 
9. Yea, J. B.W. & Yeap, B.H. (2010), “Charaterising the Cognitive Processes in 
Mathematical Investigation”, International Journal for Mathematics Teaching and 
Learning, No. 05.10, pp. 1-10. 
Người phản biện khoa học: TS. Lê Thái Bảo Thiên Trung 
(Ngày Tòa soạn nhận được bài: 25-7-2013; ngày phản biện đánh giá: 16-8-2013; 
ngày chấp nhận đăng: 16-9-2013) 
CÁC SỐ TẠP CHÍ KHOA HỌC SẮP TỚI: 
 Tháng 10/2013: Số 51(85) – Khoa học tự nhiên và công nghệ 
 Tháng 11/2013: Số 52(86) – Khoa học xã hội và nhân văn 
 Tháng 12/2013: Số 53(87) – Khoa học giáo dục 
Ban biên tập Tạp chí Khoa học rất mong nhận được sự trao đổi thông tin 
của các đơn vị bạn và được bạn đọc thường xuyên cộng tác bài vở, góp ý xây dựng.