Optimal weight design problem of spur gears
ABSTRACT
Gear is one of the most common and important components in machinery. Evaluation on durability
of gears plays crucial role in the assessment of the whole system reliability and service life. For other
parts like shafts, the gears also act as loads. Therefore, dimensions and weight of the gears should
be reduced as much as possible, contributing the size and weight reduction of the whole systems,
which is essential to be cost-effectiveness. The current research focuses on optimal weight design
problem of spur gears, such that the weight is minimized under the constraints taken from working
conditions. The weight is a function of six variables, i.e. face width, shaft diameter of pinion, shaft
diameter of gear, number of teeth on pinion, module and hardness. Constraints are derived based
on AGMA standard and engineering handbooks, including the bending strength, the surface fatigue strength, the interference condition, the condition for uniform load distribution, the torsional
strength of shaft on pinion and gear, and the center distance. The set of optimum design variables
is determined by the heuristic algorithm Grey Wolf Optimizer (GWO). The accuracy and efficiency
of the GWO in the optimal weight design problem of spur gears are assessed based on comparison
with other popular methods, such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO)
and Simulated Annealing (SA). It is noted that in previous works, some of the constraints are still
violated. Therefore, a penalty term is taken into the objective function, such that any set of design
variables that violates constraints will be considered as ``unfit'' by the algorithm. It is demonstrated
that using the proposed approach by current work, the optimal weight and the corresponding set
of design variable are very close to reference data. Yet the ad

Trang 1

Trang 2
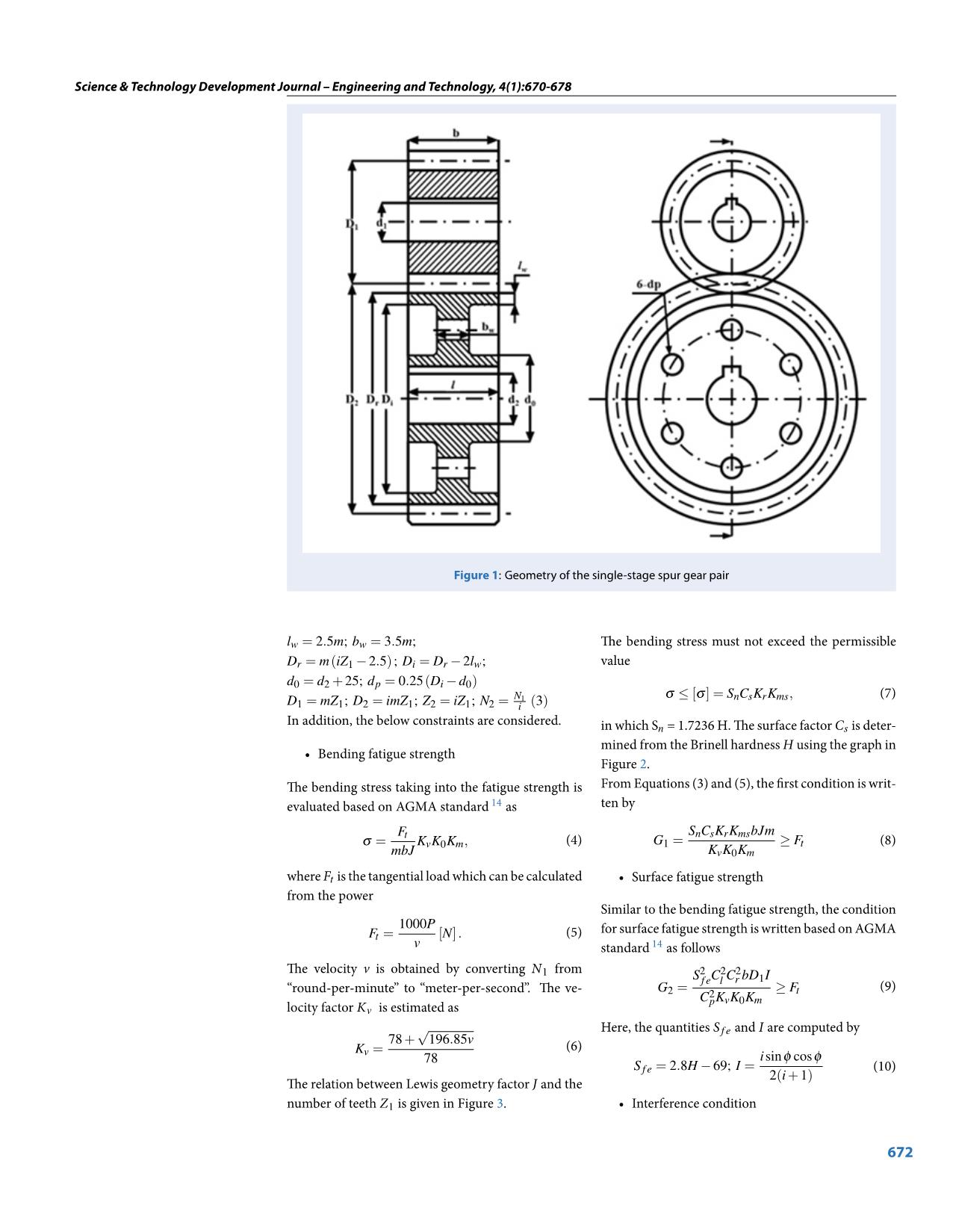
Trang 3
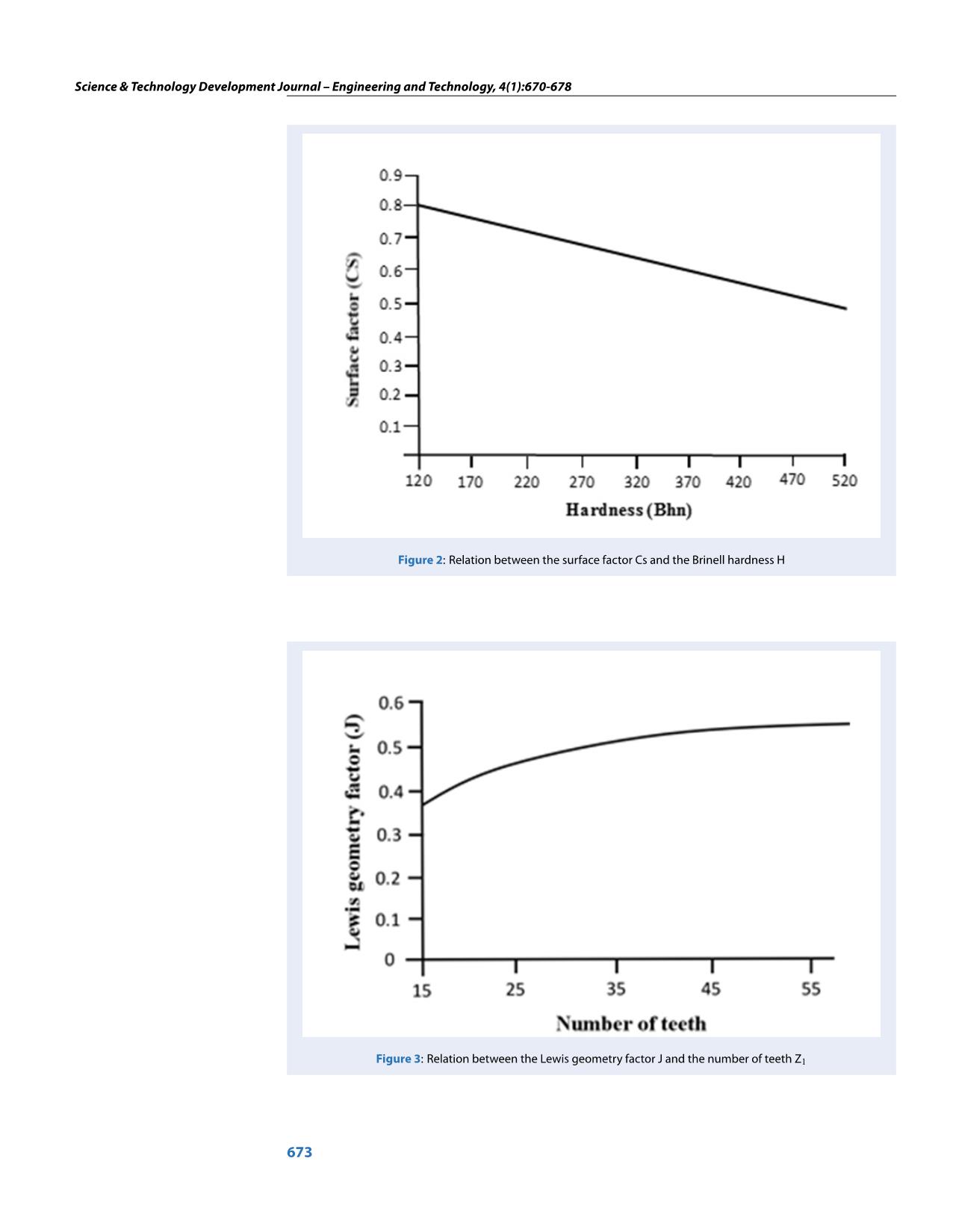
Trang 4

Trang 5

Trang 6
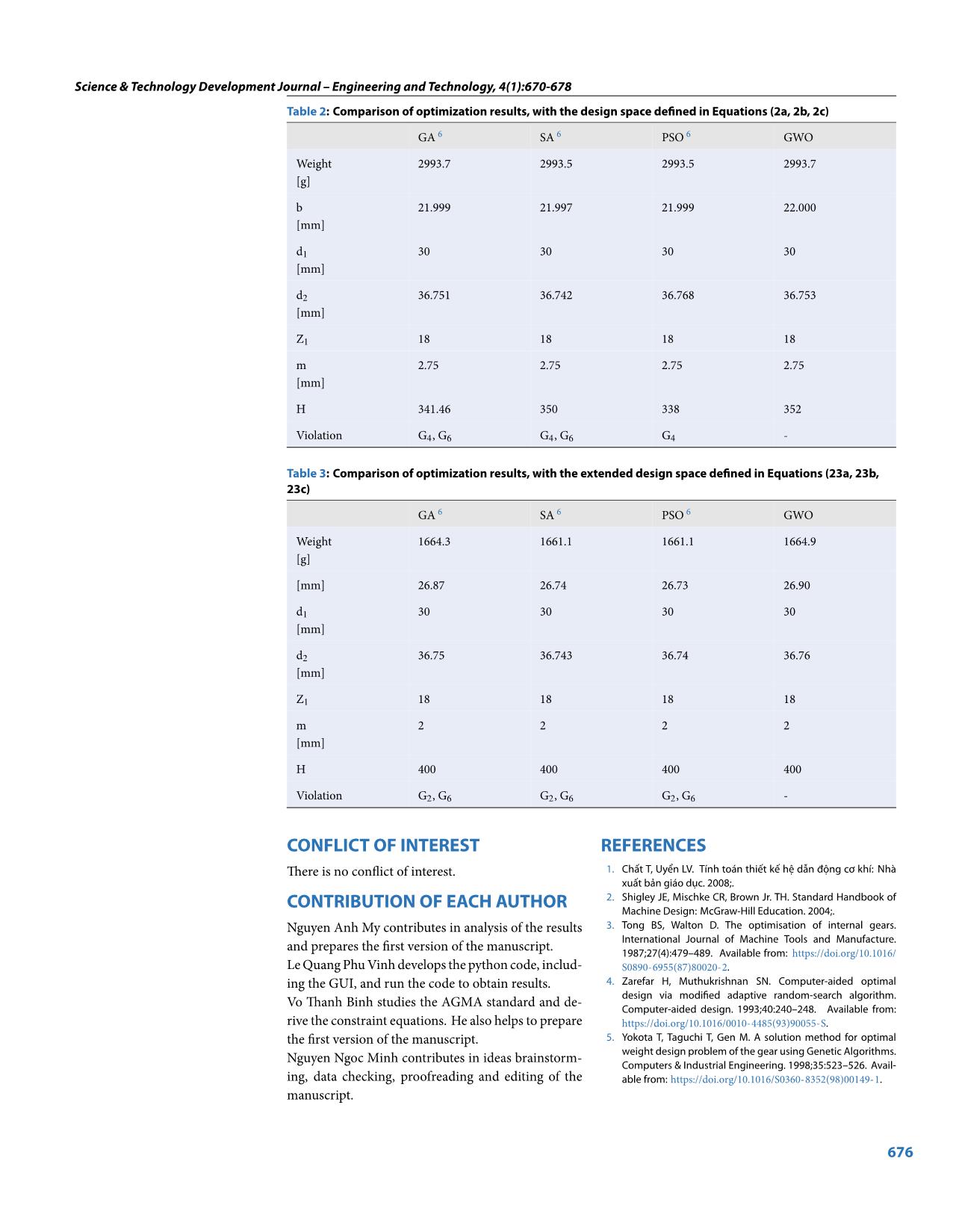
Trang 7

Trang 8

Trang 9
Tóm tắt nội dung tài liệu: Optimal weight design problem of spur gears

Science & Technology Development Journal – Engineering and Technology, 4(1):670-678
Open Access Full Text Article Research Article
Optimal weight design problem of spur gears
Nguyen Anh My1,2, Le Quang Phu Vinh1,2, Vo Thanh Binh1,2, Nguyen Ngoc Minh1,2,*
ABSTRACT
Gear is one of the most common and important components in machinery. Evaluation on durability
of gears plays crucial role in the assessment of the whole system reliability and service life. For other
Use your smartphone to scan this parts like shafts, the gears also act as loads. Therefore, dimensions and weight of the gears should
QR code and download this article be reduced as much as possible, contributing the size and weight reduction of the whole systems,
which is essential to be cost-effectiveness. The current research focuses on optimal weight design
problem of spur gears, such that the weight is minimized under the constraints taken from working
conditions. The weight is a function of six variables, i.e. face width, shaft diameter of pinion, shaft
diameter of gear, number of teeth on pinion, module and hardness. Constraints are derived based
on AGMA standard and engineering handbooks, including the bending strength, the surface fa-
tigue strength, the interference condition, the condition for uniform load distribution, the torsional
strength of shaft on pinion and gear, and the center distance. The set of optimum design variables
is determined by the heuristic algorithm Grey Wolf Optimizer (GWO). The accuracy and efficiency
of the GWO in the optimal weight design problem of spur gears are assessed based on comparison
with other popular methods, such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO)
and Simulated Annealing (SA). It is noted that in previous works, some of the constraints are still
violated. Therefore, a penalty term is taken into the objective function, such that any set of design
variables that violates constraints will be considered as ``unfit'' by the algorithm. It is demonstrated
that using the proposed approach by current work, the optimal weight and the corresponding set
of design variable are very close to reference data. Yet the advantage of the proposed approach is
exhibited in the fact that all of the constraints are satisfied.
1Department of Engineering Mechanics, Key words: Spur gear, optimal weight design, constrained optimization, Grey Wolf Optimizer
Faculty of Applied Science, Ho Chi Minh
city University of Technology
2
Vietnam National University Ho Chi 3
Minh city INTRODUCTION Walton focused on minimization of the centre dis-
tance or gear volume (separately) for internal gears,
Gears are widely found in mechanical power trans-
Correspondence
mission systems, which in turn are essential in many using three design variables. Zarefar and Muthukr-
Nguyen Ngoc Minh, Department of ishnan 4 proposed an adaptive random-search algo-
Engineering Mechanics, Faculty of fields of applications such as cars, motorbikes, air-
Applied Science, Ho Chi Minh city planes and machines. Traditionally, the gear design rithm to minimize the weight of helical gear weight
University of Technology process involves lots of empirical formulas for tooth with four variables (module, helix angle, umber of
Vietnam National University Ho Chi Minh bending strength, tooth surface fatigue strength, in- pinion teeth and face width). The problem of op-
city
terference, etc. According to handbooks and guide- timal weight design of spur gears under constraints
Email: nguyenngocminh@hcmut.edu.vn
lines, e.g. see references 1,2, the designer firstly such as bending strength of gear, torsional strength
5
History chooses the values of some certain parameters, then of shafts was formulated and solved by Yokota et al. ,
• Received: 16-11-2020 with the aid of Genetic Algorithm (GA), in which the
• the conditions are verified one by one. If any of the
Accepted: 02-3-2021 objective function (weight) is calculated based on five
• Published: 15-3-2021 conditions (e.g. tooth bending strength or tooth sur-
face fatigue strength) is not satisfied, the process has to variables (module, face width, shaft diameter of pin-
DOI :
10.32508/stdjet.v4i1.792 be repeated with new choice of parameters. Although ion, shaft diameter of gear, and the number of pinion
6
the computation can be much accelerated with the teeth). Savsani et al. further extended the problem
aid of computers, the traditional procedure is limited by considering the sixth design variable (hardness).
in the sense that the outcome is an admissible de- In fact, the hardness is not involved in the calculation
Copyright
sign but may not be an optimum one. Therefore, an of objective function (i.e. weight), but contributes in
© VNU-HCM Press. This is an open-
the computation of constraints. Two heuristic algo-
access article distributed under the optimization-based process is required to determine
ter ... al random values from 0 to
Substitute Equation (13) into (12), the condition for 1. The value of s gradually decreases from 2 to zero
( )
the shaft diameter of pinion is obtained t
s = 2 1 − , (22)
× 7 tmax
3 ≥ 4.78 10 P
G5 = d1 . (15)
τN1 in which tmax is the maximum number of iteration. It
should be emphasized that if |aα | < 1, the omega wolf
The condition for the shaft diameter of gear is deter-
will tend to join with the dominant ones to attack the
mined analogously prey (i.e. local search). On the other hand, if |aα | >
× 7 1, the omega runs away, hopefully to discover a more
3 4.78 10
G6 = d ≥ . (16) attractive prey (i.e. global search).
2 τN2
The points X2, X3 are determined using the same
•Center distance manner as mentioned in Equations (19-20).
The above algorithm of GWO 8 is for un-constrained
The distance between centers of the gear pairs is cal- problems. In order to take the constraints into ac-
culated by count, the penalty method is employed. If a con-
straint is violated, the fitness function (see Equation
D1 + D2 (1 + i)mZ1
a = = (17) (1)) is added by a penalty term, which should be a
2 2
large value. By doing so, any set of design variables
It is recommended that this value should be larger that leads to violation of constraint will be considered
than a lower bound 1 as “not fitted” by the algorithm. It is crucial to select a
large value for the penalty term. If the penalty term is
(1 + i)mZ1
G7 = ≥ 100m. (18) small, it is useless. A possible strategy is that at first,
2
the penalty term is set to zero. It is very likely that the
It is remarked that the seven constraints presented in obtained solution will violate some of the constraints.
Equations (8, 9, 11, 12, 15, 16, 18) were also consid- Let us call the corresponding weight in this case as
6
ered by reference , although the derivation was not “f 0”, the penalty term then can be estimated by mul-
explicitly mentioned. tiplying “f 0” with a factor of 1000.
674
Science & Technology Development Journal – Engineering and Technology, 4(1):670-678
RESULTS AND DISCUSSION CONCLUSION
The proposed GWO algorithm for constrained op- The meta-heuristic GWO algorithm has been success-
timization (the third Section) is implemented in fully applied to the constrained optimization problem
Python to solve the problem of finding the optimal of finding optimal weight design of spur gear. The
weight design of spur gears (the second Section). constraints are derived from working conditions with
Results obtained by the present GWO algorithm are reference to AGMA standard and engineering hand-
displayed in Table 2, showing a comparison with those books. The problem is challenging, as results reported
obtained by GA, SA and PSO 6, for the design space in previous works by other authors still encounter vi-
defined in Equations (2a, 2b, 2c). The population olation of constraints. The current results show that
size and the maximum number iteration are chosen an optimal set of design variables that satisfy all the
exactly the same with Savsani et al. 6, i.e. 20 wolves constraints can be obtained.
and 300 iterations. It is observed that both the weight All of the six design variables have their roles. The
and the corresponding “optimized” set of design vari- first five variables are geometry parameters, which di-
rectly contribute to the weight (objective function).
ables are quite similar to those reported in reference 6.
Although the hardness H does not contribute to the
However, the notable difference is that the set of de-
weight, it represents the material strength. Indeed,
sign variables determined by GWO satisfy all the con-
H is required during evaluation of bending fatigue
straints. All the results by Savsani et al. 6, regardless
strength (constraint G ) and surface fatigue strength
GA, SA or PSO algorithm, still encounter violation of 1
(constraint G2). Loosely speaking, higher value of
some constraints.
hardness H leads to higher strength, which allows the
For further demonstration, the ranges of design vari-
reduction of geometry parameters. Therefore, H in-
ables are extended as follows
directly affects the total weight. However the manu-
Real values:
facturing cost may increase as well. For practical pur-
pose, additional constraint on manufacturing cost can
10 ≤ b ≤ 35; 10 ≤ d1 ≤ 30; 10 ≤ d2 ≤ 40 (23a)
be included.
Integer values: In GWO algorithm, the position of each wolf is up-
dated based on the information of the three best
18 ≤ Z ≤ 25; 200 ≤ H ≤ 400 (23b)
1 wolves, i.e. the alpha, the beta, and the delta. Al-
Discrete values: though the technique may enhance the exploitation, it
requires more calculation and more storage space. It
∈ { }
m 1, 1.25, 1.5, 2, 2.75, 3, 3.5, 4 (23c) is noted that in GA, the update of each chromosome
does not involve information of the best solution. In
Due to broader ranges of variables, the maximum
PSO, two special solutions, i.e. the current best and
number of iteration is also increased to 500. Opti-
worst ones, are required. Furthermore, it is argued by
mized results for the extended design space are pre-
Gao and Zhao 16 that the role of alpha, the beta, and
sented in Table 3. In this case, the weight obtained by
the delta should not be the same as in Equation (19).
GWO is slightly higher than that by GA, SA, and PSO
Equation (19) should be rewritten as a weighted aver-
as reported in Savsani et al. 6. However, again it is im-
age, in which the influence will be assigned from high-
portant that some constraints are violated in Savsani
est to lowest value to the alpha, the beta and the delta,
6
et al. , while no violation is encountered by the pro- respectively. However, the task of improving GWO is
posed GWO. not within the scope of the current work.
20 wolves and 300 iterations are used to obtain the re-
sults in Table 2. By using a computer with Intel(R) ACKNOWLEDGEMENT
Core(TM) i7-10750H CPU @ 2.60GHz and 8.00 GB This work is financially supported by the Ho Chi Minh
RAM, the computational time is approximately 15 city University of Technology under the grant SVCQ-
minutes (no parallel computing is involved). For the 2020-KHUD-48.
example presented in Table 3, 20 wolves and 500 it-
erations are used. The elapsed time in this case is LIST OF ABBREVIATIONS
nearly 20 minutes. Unfortunately, there is no in- AGMA: American gear manufacturers association
formation available on the computational cost in the GWO: Grey Wolf Optimizer
references 5,6. Nevertheless, it is reasonable to con- GA: Genetic Algorithm
sider that the current approach is more efficient be- SA: Simulated Annealing
cause the solution is achieved without any violation PSO: Particle Swarm Optimization
of constraints. GUI: Graphical User Interface
675
Science & Technology Development Journal – Engineering and Technology, 4(1):670-678
Table 2: Comparison of optimization results, with the design space defined in Equations (2a, 2b, 2c)
GA 6 SA 6 PSO 6 GWO
Weight 2993.7 2993.5 2993.5 2993.7
[g]
b 21.999 21.997 21.999 22.000
[mm]
d1 30 30 30 30
[mm]
d2 36.751 36.742 36.768 36.753
[mm]
Z1 18 18 18 18
m 2.75 2.75 2.75 2.75
[mm]
H 341.46 350 338 352
Violation G4, G6 G4, G6 G4 -
Table 3: Comparison of optimization results, with the extended design space defined in Equations (23a, 23b,
23c)
GA 6 SA 6 PSO 6 GWO
Weight 1664.3 1661.1 1661.1 1664.9
[g]
[mm] 26.87 26.74 26.73 26.90
d1 30 30 30 30
[mm]
d2 36.75 36.743 36.74 36.76
[mm]
Z1 18 18 18 18
m 2 2 2 2
[mm]
H 400 400 400 400
Violation G2, G6 G2, G6 G2, G6 -
CONFLICT OF INTEREST REFERENCES
There is no conflict of interest. 1. Chất T, Uyển LV. Tính toán thiết kế hệ dẫn động cơ khí: Nhà
xuất bản giáo dục. 2008;.
2. Shigley JE, Mischke CR, Brown Jr. TH. Standard Handbook of
CONTRIBUTION OF EACH AUTHOR Machine Design: McGraw-Hill Education. 2004;.
Nguyen Anh My contributes in analysis of the results 3. Tong BS, Walton D. The optimisation of internal gears.
International Journal of Machine Tools and Manufacture.
and prepares the first version of the manuscript. 1987;27(4):479–489. Available from: https://doi.org/10.1016/
Le Quang Phu Vinh develops the python code, includ- S0890-6955(87)80020-2.
ing the GUI, and run the code to obtain results. 4. Zarefar H, Muthukrishnan SN. Computer-aided optimal
design via modified adaptive random-search algorithm.
Vo Thanh Binh studies the AGMA standard and de- Computer-aided design. 1993;40:240–248. Available from:
rive the constraint equations. He also helps to prepare https://doi.org/10.1016/0010-4485(93)90055-S.
the first version of the manuscript. 5. Yokota T, Taguchi T, Gen M. A solution method for optimal
Nguyen Ngoc Minh contributes in ideas brainstorm- weight design problem of the gear using Genetic Algorithms.
Computers & Industrial Engineering. 1998;35:523–526. Avail-
ing, data checking, proofreading and editing of the able from: https://doi.org/10.1016/S0360-8352(98)00149-1.
manuscript.
676
Science & Technology Development Journal – Engineering and Technology, 4(1):670-678
6. Savsani V, Rao RV, Vakharia DP. Optimal weight design of 11. Zhang S, Zhou Y. Template matching using grey wolf op-
a gear train using particle swarm optimization and simu- timizer with lateral inhibition. Optik. 2017;130:1229–1243.
lated annealing algorithms. Mechanism and Machine Theory. Available from: https://doi.org/10.1016/j.ijleo.2016.11.173.
2009;45:531–541. Available from: https://doi.org/10.1016/j. 12. Emary E, Zawbaa HM, Grosan C, Hassenian AE. Binary grey
mechmachtheory.2009.10.010. wolf optimization approaches for feature selection. Neuro-
7. Miler D, Loncar A, ZD, and Domitran Z. Influence of profile computing. 2016;172(8):371–381. Available from: https://doi.
shift on the spur gear optimization. Mechanism and Machine org/10.1016/j.neucom.2015.06.083.
Theory. 2017;117:189–197. Available from: https://doi.org/10. 13. Eswaramoorthy S, Sivakumaran N, Sekaran S. Grey wolf opti-
1016/j.mechmachtheory.2017.07.001. mization based parameter selection for support vector ma-
8. Mirjalili S, Mirjalili SM, Lewis A. Grey Wolf Optimizer. Advances chines. COMPEL - The international journal for computation
in Engineering Software. 2014;69:46–61. Available from: and mathematics in electrical and electronic engineering.
https://doi.org/10.1016/j.advengsoft.2013.12.007. 2016;35(5):1513–1523. Available from: https://doi.org/10.
9. Lakum A, Mahajan V. Optimal placement and sizing of mul- 1108/COMPEL-09-2015-0337.
tiple active power filters in radial distribution system using 14. American National Standard: Fundamental Rating Factors
grey wolf optimizer in presence of nonlinear distributed gen- and Calculation Mehods for Involute Spur and Helical Gear
eration. Electric Power System Research. 2019;173:281–290. Teeth: American Gear Manufacturers Association. 2001;.
Available from: https://doi.org/10.1016/j.epsr.2019.04.001. 15. Norton RL. Machine Design - An integrated approach: Pear-
10. Song X, Tang L, Zhao S, Zhang X, Li L, Huang J, et al. Grey Wolf son. 2020;.
Optimizer for parameter estimation in surface waves. Soil Dy- 16. Gao ZM, Zhao J. An improved Grey Wolf Optimization algo-
namics and Earthquake Engineering. 2015;75:147–157. Avail- rithm with variable weights. Computational Intelligence and
able from: https://doi.org/10.1016/j.soildyn.2015.04.004. Neuroscience. 2019;2019:2981282. PMID: 31281334. Avail-
able from: https://doi.org/10.1155/2019/2981282.
677
Tạp chí Phát triển Khoa học và Công nghệ – Kĩ thuật và Công nghệ, 4(1):670-678
Open Access Full Text Article Bài nghiên cứu
Tối ưu hóa khối lượng của cặp bánh răng trụ răng thẳng
Nguyễn Anh Mỹ1,2, Lê Quang Phú Vinh1,2, Võ Thanh Bình1,2, Nguyễn Ngọc Minh1,2,*
TÓM TẮT
Bánh răng là chi tiết phổ biến và quan trọng trong máy móc. Việc đánh giá độ bền của bánh răng
vì thế có ý nghĩa thiết yếu đối với độ tin cậy và tuổi thọ làm việc của toàn hệ thống. Đối với các chi
Use your smartphone to scan this tiết khác, chẳng hạn như trục, bánh răng còn đóng vai trò là tải. Vì vậy, kích thước và khối lượng
QR code and download this article bánh răng cần được hết sức tiết giảm, nhằm làm thu gọn kích thước và khối lượng của toàn hệ
thống, từ đó giảm được chi phí. Nghiên cứu hiện tại tập trung vào tối ưu hóa khối lượng của cặp
bánh răng trụ răng thẳng, xét đến những ràng buộc xuất phát từ điều kiệ làm việc. Các biến thiết
kế được lựa chọn là bề rộng răng, đường kính trục ở bánh răng chủ động, đường kính trục ở bánh
răng bị động, số răng ở bánh răng chủ động, mô-đun và độ cứng. Các ràng buộc được xây dựng
với tham khảo từ tiêu chuẩn AGMA và sổ tay thiết kế, bao gồm độ bền uốn, độ bền mỏi tiếp xúc,
điều kiện ăn khớp, điều kiện phân bố tải trọng khi tiếp xúc, độ bền xoắn trục tại vị trí lắp bánh răng
và khoảng cách trục. Bộ giá trị biến thiết kế tối ưu được xác định thông qua giải thuật tìm kiếm
sói xám (Grey Wolf Optimizer – GWO). Tính chính xác và hiệu quả của GWO được so sánh với các
phương pháp khác như giải thuật di truyền (Genetic Algorithm – GA), giải thuật bầy đàn (Particle
Swarm Optimization - PSO) và giải thuật mô phỏng luyện kim (Simulated Annealing – SA). Kết quả
thu được từ các nghiên cứu trước đều ghi nhận sự vi phạm đối với một vài điều kiện ràng buộc.
Trong nghiên cứu hiện tại, hàm mục tiêu được cộng thêm thành phần ``phạt'' để đảm bảo bất kỳ
tập hợp biến thiết kế nào vi phạm điều kiện ràng buộc đều bị thuật toán coi là không phù hợp.
Kết quả cho thấy, lời giải thu được từ phương pháp đề xuất trong nghiên cứu hiện tại có sự tương
đồng tốt với các tài liệu tham khảo, cả về khối lượng bánh răng và các giá trị biến thiết kế tương
ứng. Ưu điểm của nghiên cứu hiện tại được thể hiện qua việc tất cả các điều kiện ràng buộc đều
được thỏa mãn.
Từ khoá: Bánh răng trụ răng thẳng, thiết kế tối ưu khối lượng, tối ưu hóa có ràng buộc, Grey Wolf
1Bộ môn Cơ kỹ thuật, Khoa Khoa học Optimizer
Ứng dụng, Trường Đại học Bách khoa
Thành phố Hồ Chí Minh
2Đại học Quốc gia Thành phố Hồ Chí
Minh
Liên hệ
Nguyễn Ngọc Minh, Bộ môn Cơ kỹ thuật,
Khoa Khoa học Ứng dụng, Trường Đại học
Bách khoa Thành phố Hồ Chí Minh
Đại học Quốc gia Thành phố Hồ Chí Minh
Email: nguyenngocminh@hcmut.edu.vn
Lịch sử
• Ngày nhận: 16-11-2020
• Ngày chấp nhận: 02-3-2021
• Ngày đăng: 15-3-2021
DOI : 10.32508/stdjet.v4i1.792
Bản quyền
© ĐHQG Tp.HCM. Đây là bài báo công bố
mở được phát hành theo các điều khoản của
the Creative Commons Attribution 4.0
International license.
Trích dẫn bài báo này: Mỹ N A, Vinh L Q P, Bình V T, Minh N N. Tối ưu hóa khối lượng của cặp bánh
răng trụ răng thẳng. Sci. Tech. Dev. J. - Eng. Tech.; 4(1):670-678.
678File đính kèm:
 optimal_weight_design_problem_of_spur_gears.pdf
optimal_weight_design_problem_of_spur_gears.pdf

