Numerical modelization of the oil film pressure for a hydrodynamic tilting - pad thrust bearing

 Journal of Science & Technology 146 (2020) 025-030 
 Numerical Modelization of the Oil Film Pressure for a Hydrodynamic 
 Tilting-Pad Thrust Bearing 
 Le Anh Dung, Tran Thi Thanh Hai * 
 Hanoi University of Science and Technology, No.1 Dai Co Viet str., Hai Ba Trung dist., Hanoi, Vietnam 
 Received: June 17, 2020; Accepted: November 12, 2020 
 Abstract 
 This study analyses the hydrodynamic characteristic of the tilting pad thrust bearing. Research content is 
 simultaneously solving the Reynolds equation, force equilibrium equation, and momentum equilibrium 
 equations. Reynolds equation is solved by utilizing the finite element method with Galerkin weighted residual, 
 thereby determines the pressure at each discrete node of the film. Force and momentums are integrated from 
 pressure nodes by Gaussian integral. Finally, force and momentum equilibrium equations are solved using 
 Newton-Raphson iterative to achieve film thickness and inclination angles of the pad at the equilibrium 
 position. The results yielded the film thickness, the pressure distribution on the whole pad and different 
 sections of the bearing respected to the radial direction. The high-pressure zone is located at the low film 
 thickness zone and near the pivot location. 
 Keywords: Hydrodynamic tilting-pad thrust bearing, equilibrium position, finite element method. 
1. Introduction1 Fig.1 shows the diagram of a pad in pivot tilting 
 pad thrust bearing. Here, the pad is placed onto a pivot 
 Tilting pad thrust bearings are used in rotary 
 that is eccentric from the middle of the pad, to form the 
machineries, allow for the thrust load operation at the 
 oil wedge as hydrodynamic theory. The pressure in the 
average of rotation and support a heavy load. 
 wedge generates the force onto the pad surface making 
Hydrodynamic thrust bearing based on hydrodynamic 
 the pad to tilt at an angle respected to the r-axis and the 
lubrication. 
 θ -axis. r and θ are two directions of polar 
 In 2012, D. V. Srikanth et. al. [1] studied a large coordinates. The inner and outer radius of the pad are 
tilting pad thrust bearing angular stiffness. In 2014, 
 r1 and r2, θ pad is the pad angle, θ p and rp are the 
Najar and Harmain [2] performed a numerical study on 
 position of the pivot, hp is the film thickness at pivot 
pressure profiles in the hydrodynamic thrust bearing. 
 location, α  and α are the inclinations of the pad 
Annan Guo et.al [3] experiment static and dynamic r θ
characteristics of tilting pad thrust bearing in the same along the radial and circumferential direction, ω is 
year. In 2018, Mostefa K. et al. [4] analyzed the effect the angular velocity of the collar. 
of dimple geometries on textured tilting pad thrust 
bearing using a finite difference method. 
 In Vietnam, studies about hydrodynamic tilting 
pad bearing are few. Most recently, Hai T.T.T et al [5] 
compared a numerical calculation of a hydrodynamic 
fixed pad thrust bearing with experiment results. 
Besides Dung Le Anh et al. [6] perform a numerical 
modelization of oil film pressure in hydrodynamic 
journal bearing under a steady load. 
 This research analyzes the pressure and oil film 
thickness of a pivot tilting pad thrust bearing at 
hydrodynamic lubrication. 
2. Thrust bearing and the equations 
2.1. Tilting pad thrust bearing 
 Fig. 1. Diagram of a pivot tilting pad thrust bearing. 
*Corresponding author: Tel.: (+84) 978263926 
Email: hai.tranthithanh@hust.edu.vn 
 25 
 Journal of Science & Technology 146 (2020) 025-030 
2.2. The equations 33∂∂WWii∂∂∂pph1
 ∬  −−rh h − Wi .6µω r dS +
2.2.1 The Reynolds equation: S ∂∂rrr ∂∂θθ ∂ θ
 33∂∂pp1
 Obtained from the Naviers-Stockes and ++∮Wir rh n dττ  W i.0 h nθ d =
 ∮b
continuity equations for an incompressible, isoviscous, ∂∂rrθ
steady-state and laminar flow fluid, the Reynolds (5) 
equation is written in polar coordinates [7]: n
 = =
 p can be expressed as: p∑ Npii N.{ p} 
 ∂ ∂p 1 ∂∂  ph ∂ =
 rh33+=h 6µωr (1) i 1
 ∂ ∂  ∂∂θθ  ∂ θ
 r rr   where n is the total number of mesh points, N is the 
where p is oil film pressure, r is radial direction, θ is global polynomials function vector. 
circumferential direction, h is oil film thickness, µ is 
dynamic viscosity, ω is angular velocity of the shaft. 
 The boundary condition chosen for the Reynolds 
equation is: 
 pr(θ =0,) = 0 ;  pr(θθ=pad ,0) = 
 p(θ,0 rr=1 ) = ;  p(θ,0 rr=2 ) = 
2.2.2 Oil film thickness equation: 
 =+−θθ − α +
 h hpp r rcos( p) sin( θ ) Fig. 2. Diagram of a tilting pad thrust bearing 
 +−rsin(θθpr) sin( α) (2) With Galerkin weight residual, the weighting 
 function Wi is chosen equal to the shape function Ni . 
2.2.3 Force and momentum equilibrium equations: 
 Combined with boundary condition, we have: 
 The pressure distribution is integrated over the 
 ∂   ∂
pad area to give the resulting force and the moments in 3 p 1 3 p
 ∮Wir rh n dτ = 0 and ∮ Whi .0 ndθ τ = 
two perpendicular directions around the pivot point. ∂r b r ∂θ
   Equation (5) becomes: 
 Fzp h ,,ααθ r=  prd θ dr= W 
 ( ) ∬S
   ∂∂∂∂NN
   33{NNii} { jj} 1 { } { }
 2 ∬  rh + h dS{ p} 
 Mxp h ,,ααθ r= pr sin θθ −=pd θ dr 0 (3) S
 ( ) ∬S ( ) ∂∂r rr ∂∂θθ
     ∂
 αα =θθ −− θ = h
 Myp( h ,,θ r) ∬  p( r.cos( p) r p) rd dr 0 =∬   −{Ni }.6µω r dS (6) 
 S S ∂θ
3. Algorithm Rewrite the left side of equation (4) as a matrix 
3.1 Solving Reynolds equation form: 
 The pad domain is discreted into a 4-node finite ∂∂NNii
 3 ∂∂NNin
element mesh as Fig. 2. Here coordinates in polar form ∂∂θ r h 
   0 ∂∂θθ 
is change to the reference coordinates ξη, . Using ∬   r .{ pi } rdθ dr
 ( ) S ∂∂
 3 NNin
 ∂∂NN0 rh 
finite element method, integrate equation (1) over the nn ∂∂rr
domain S: ∂∂θ r
   ∂ ∂p 1 ∂  ∂ ph ∂  (7) 
 33+−=µω
∬ W i  rh  h60 r dS 
 S ∂r ∂ rr  ∂∂θθ  ∂ θ The conversion from polar coordinates to 
 (4) reference coordinate system is featured by Jacobi 
 matrix J: 
where Wi is weight functions. 
 Integrate by part equation (4), we have: 
 26 
 Journal of Science & Technology 146 (2020) 025-030 
 ∂∂θ r nn∂∂NNjj ∂∂∂
 θ FFFzzz
 ∑∑=   ii= r 
 ∂∂ξξii11 ∂ ξ ∂ ξ ∂∂∂h αα
 J = =  (8) prθ
 ∂∂θ  ∂ ∂ 
 rNnnjj N ∂∂∂
   θ r MMMxxx
 ∑∑ii=11ii= D = − (14) 
 ∂∂ηη∂∂ηη ∂∂∂h αα
 prθ
 Thus (7) becomes: ∂∂∂MMMyyy
 ∂∂∂αα
 hprθ
 ∂∂NNii
 ∂∂θ 3
 r h Substitute (13) to (14), we have: 
 −1 0
∬   ××J r × 
 S  ttt
 3 
  Sp... Spαα Sp
 ∂∂NN 0 rh hprθ
 nn  
 ttt
 ∂∂θ r D= −  Rp...h Rpαα Rp 
 prθ
 ttt
 Tp...h Tpαα Tp
 ∂∂NNin prθ
 
 − ∂∂θθ t
 ××J1 ×pr × S
 { i } 
 ∂∂NNin (9) t 
  = − Rp pαα p (15) 
  hprθ
 ∂∂rr t
 T
 ×det( J) ×=× dξη d[ K] { pi }
 ∂p ∂p ∂p
 where p = , p = , p = 
 The right side of the equation (6) becomes: hp αθ αr
 ∂hp ∂αθ ∂αr
   ∂h
 {F}  = −{ Ni }.6µω r rd θ dr
 ∬S p , p , p are calculated as follows: 
 ∂θ hp αθ αr
 (10) 
   ∂h
 = −∬ { Ni }.6µω r r . det( J) . dξ d η Derive equation (11) respected to h , α , α : 
 S ∂θ p θ r
Thus, equation (6) is rewritten as: ∂[K ] ∂∂{ pFi } { }
 { pK} +=[ ] (16) 
 ∂∂∂kkki
 [Kp].{ i } = { F} (11) 
 with kh= , α , α . 
 Solve the above equation with boundary p θ r
condition, we can get pressure value at all nodes. 
 ∂∂{ pF} 1 { } ∂[K ]
 Thus, i = − p (17) 
3.2 Solve force and momentum equation { i }
 ∂kKk[ ]  ∂∂ k
 Let: 
 where: 
 = θ
 S∬   rd dr ∂[K ]   ∂h
 S = 3h2 ×
 ∬S
   ∂∂kk
 2 
 R=∬   r sin (θθ− p )d θ dr (12) 
 S ∂∂{NN} ∂∂{NNjj} 1 { } { }
 ×+r iirdθ dr
 ∂∂ ∂∂θθ
   r rr
 T=∬  ( r.cos(θθ −−pp) r) rd θ dr 
 S (18) 
 αα = t
 We get:. Fhzp( ,,θ r) S{ p i} ∂{F}   ∂∂h
 =  −{Ni }.6µω r rdθ dr (19) 
 ∬S 
 t ∂kk∂∂θ
 Mhxp( ,,ααθ r) = Rp{ i} (13) 
 In order to solve the nonlinear equation, Newton- 
 t
 Mhyp( ,,ααθ r) = Tp{ i} Raphson method is commonly used due to its rapid 
 convergence and highly accurate approximation. Let 
 The Jacobian matrix related to the equilibrium t
 = αα
position is: uhpr, θ ,  be the present step of the equilibrium 
 position, unew be the new guess value for the new step. 
 Thus, the iterative process is given by: 
 27 
 Journal of Science & Technology 146 (2020) 025-030 
 t
 =−− −− 4. Results 
 unew u D\ Fz WM ,x 0, M y 0 
 The present study bearing is a large tilting pad 
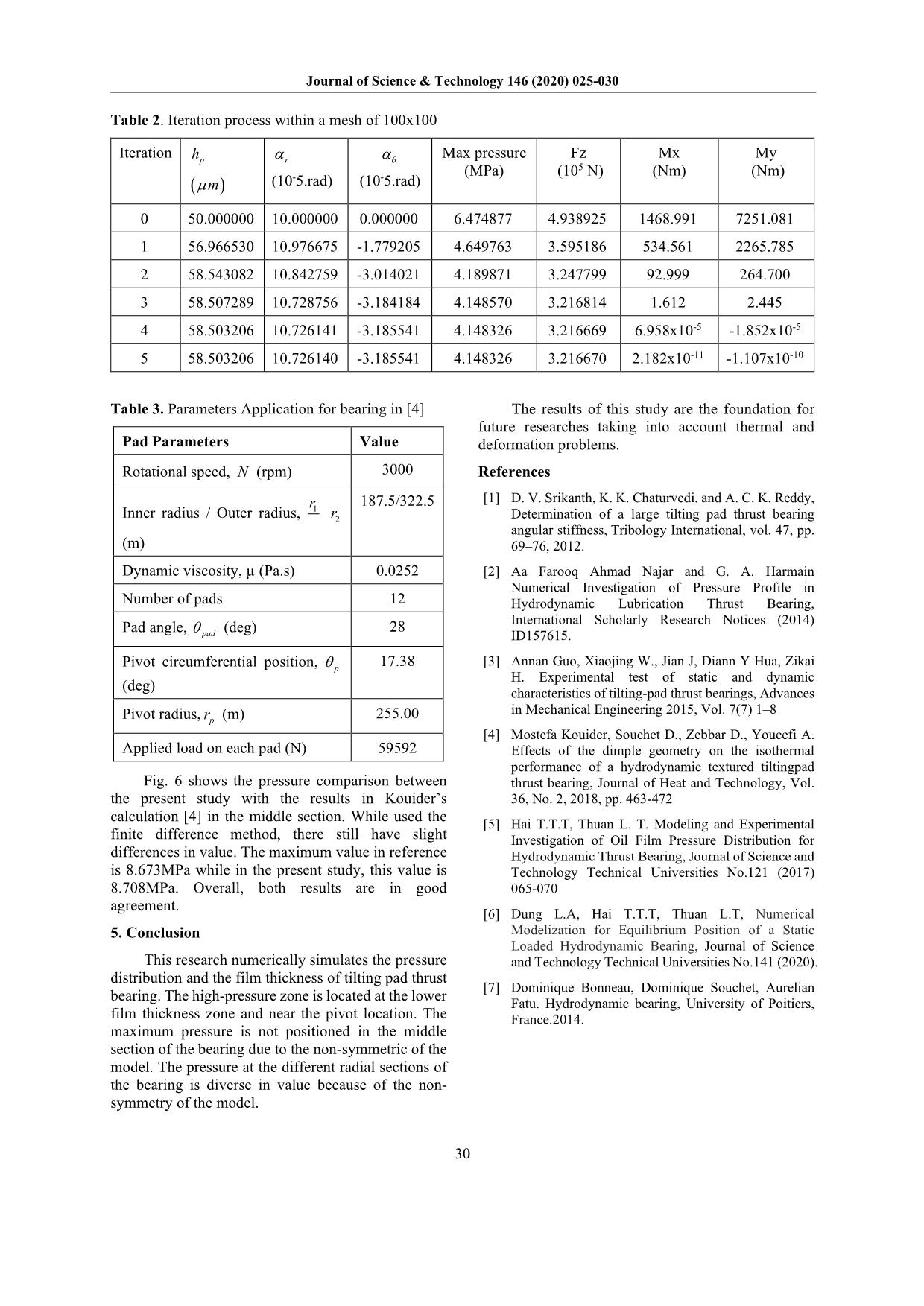
 This iteration process ends when the following bearing and its parameters are described in Table 1. 
error bound condition err is satisfied: The program is written in MATLAB 2019a. 
 kk+1 Table 2 illustrates the iteration process of a 
 uunew − FWz −
 ≤ err & ≤ err & Mx ≤ err 100x100 elements mesh grid. The result shows with a 
 k +1 F
 u z good initial guess, high accuracy can be achieved after 
 -5 a few iterative steps due to the high convergence rate 
& My ≤ err with err=10 . 
 of the Newton-Raphson method. The circumferential 
 Within the algorithm described above, inclination is much lower than the radial inclination as 
programming diagram is shown in Fig.3. A set of the result of pivot location is offset a distance from the 
initial values are used to calculate the pressure, film center of the pad with respect to the circumferential 
thickness and inclinations. Then in each iteration, new direction. 
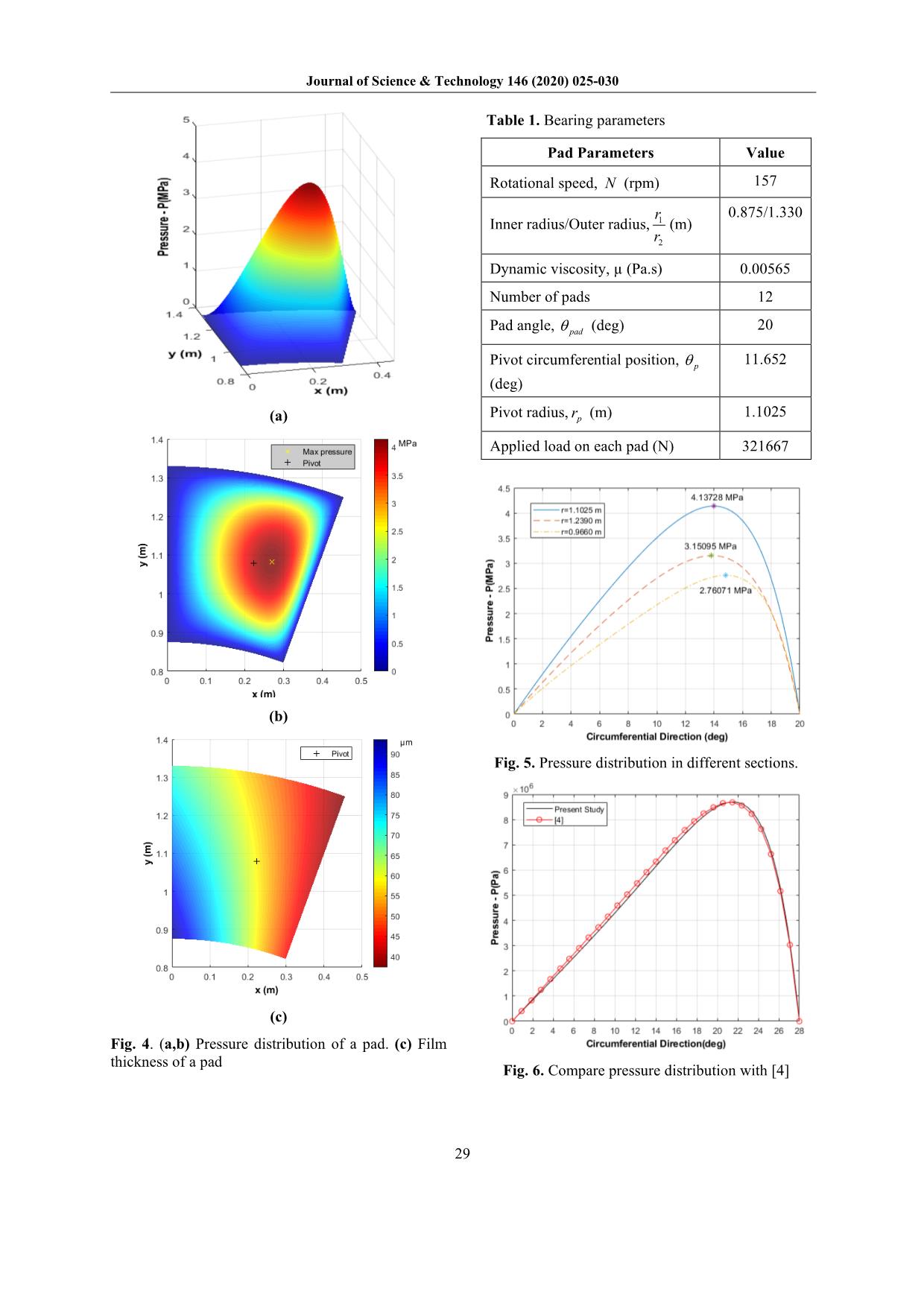
values are updated until the solution converges. Fig.4a, 4b show the pressure distribution of a pad. 
 Film thickness is described in Fig.4c. The pressure is 
 yielded in the Cartesian coordinates for easier 
 description. The high-pressure zone is located at the 
 center zone of the pad, near the pivot location, and 
 leans toward low film thickness. This is reasonable 
 while the equivalent film force on the whole pad is 
 needed to impact the pivot location to create an 
 equilibrium state. The maximum 
 pressure on the whole pad is 
 4.14833 MPa at the
 (θ,rm) = ( 14o ,1.08885  ) . 
 This position is not located in 
 the middle section of the pad along 
 the radial direction because the film 
 thickness of the tilting pad thrust 
 bearing can vary along the radial 
 direction. 
 Fig.5 indicates the pressure 
 distribution at different sections of 
 the pad with respect to the radial 
 axis. At the middle section of the 
 pad, the highest-pressure-value is 
 4.13729 MPa at θ = 14o , slightly 
 lower than the maximum pressure of 
 the whole field. At two symmetric 
 sections r = 1.2390m and 
 r = 0.9660m, the section near the 
 outer radius shows higher pressure 
 than the one near the inner radius. 
 This is reasonable due to the non-
 symmetry of the model. 
 In order to check the validation of the program, 
 author compared with the study of Kouider [4] with 
 specific parameters showed in Table 3. 
 Fig. 3. Programming Algorithm 
 28 
 Journal of Science & Technology 146 (2020) 025-030 
 Table 1. Bearing parameters 
 Pad Parameters Value 
 Rotational speed, N (rpm) 157 
 r 0.875/1.330 
 Inner radius/Outer radius, 1 (m) 
 r2
 Dynamic viscosity, µ (Pa.s) 0.00565 
 Number of pads 12 
 Pad angle, θ pad (deg) 20 
 Pivot circumferential position, θ p 11.652 
 (deg) 
 (a) Pivot radius, rp (m) 1.1025 
 Applied load on each pad (N) 321667 
 (b) 
 Fig. 5. Pressure distribution in different sections. 
 (c) 
Fig. 4. (a,b) Pressure distribution of a pad. (c) Film 
thickness of a pad 
 Fig. 6. Compare pressure distribution with [4] 
 29 
 Journal of Science & Technology 146 (2020) 025-030 
Table 2. Iteration process within a mesh of 100x100
 Iteration hp αr αθ Max pressure Fz Mx My 
 5
 - - (MPa) (10 N) (Nm) (Nm) 
 (µm) (10 5.rad) (10 5.rad) 
 0 50.000000 10.000000 0.000000 6.474877 4.938925 1468.991 7251.081 
 1 56.966530 10.976675 -1.779205 4.649763 3.595186 534.561 2265.785 
 2 58.543082 10.842759 -3.014021 4.189871 3.247799 92.999 264.700 
 3 58.507289 10.728756 -3.184184 4.148570 3.216814 1.612 2.445 
 4 58.503206 10.726141 -3.185541 4.148326 3.216669 6.958x10-5 -1.852x10-5 
 5 58.503206 10.726140 -3.185541 4.148326 3.216670 2.182x10-11 -1.107x10-10 
Table 3. Parameters Application for bearing in [4] The results of this study are the foundation for 
 future researches taking into account thermal and 
 Pad Parameters Value deformation problems. 
 Rotational speed, N (rpm) 3000 References 
 [1] D. V. Srikanth, K. K. Chaturvedi, and A. C. K. Reddy, 
 r1 187.5/322.5 
 Inner radius / Outer radius, r2 Determination of a large tilting pad thrust bearing 
 angular stiffness, Tribology International, vol. 47, pp. 
 (m) 69–76, 2012. 
 Dynamic viscosity, µ (Pa.s) 0.0252 [2] Aa Farooq Ahmad Najar and G. A. Harmain 
 Numerical Investigation of Pressure Profile in 
 Number of pads 12 Hydrodynamic Lubrication Thrust Bearing, 
 Pad angle, θ (deg) 28 International Scholarly Research Notices (2014) 
 pad ID157615. 
 Pivot circumferential position, θ p 17.38 [3] Annan Guo, Xiaojing W., Jian J, Diann Y Hua, Zikai 
 H. Experimental test of static and dynamic 
 (deg) characteristics of tilting-pad thrust bearings, Advances 
 in Mechanical Engineering 2015, Vol. 7(7) 1–8 
 Pivot radius, rp (m) 255.00 
 [4] Mostefa Kouider, Souchet D., Zebbar D., Youcefi A. 
 Applied load on each pad (N) 59592 Effects of the dimple geometry on the isothermal 
 performance of a hydrodynamic textured tiltingpad 
 Fig. 6 shows the pressure comparison between thrust bearing, Journal of Heat and Technology, Vol. 
the present study with the results in Kouider’s 36, No. 2, 2018, pp. 463-472 
calculation [4] in the middle section. While used the 
 [5] Hai T.T.T, Thuan L. T. Modeling and Experimental 
finite difference method, there still have slight Investigation of Oil Film Pressure Distribution for 
differences in value. The maximum value in reference Hydrodynamic Thrust Bearing, Journal of Science and 
is 8.673MPa while in the present study, this value is Technology Technical Universities No.121 (2017) 
8.708MPa. Overall, both results are in good 065-070 
agreement. 
 [6] Dung L.A, Hai T.T.T, Thuan L.T, Numerical 
5. Conclusion Modelization for Equilibrium Position of a Static 
 Loaded Hydrodynamic Bearing, Journal of Science 
 This research numerically simulates the pressure and Technology Technical Universities No.141 (2020). 
distribution and the film thickness of tilting pad thrust 
 [7] Dominique Bonneau, Dominique Souchet, Aurelian 
bearing. The high-pressure zone is located at the lower Fatu. Hydrodynamic bearing, University of Poitiers, 
film thickness zone and near the pivot location. The France.2014. 
maximum pressure is not positioned in the middle 
section of the bearing due to the non-symmetric of the 
model. The pressure at the different radial sections of 
the bearing is diverse in value because of the non-
symmetry of the model. 
 30