Numerical investigation of microstructure effect on acoustic properties of underwater anechoic coatings
This paper presents a simulation-based model for predicting the acoustic properties of
underwater anechoic structures with its main layer made of viscoelastic sound absorbing
materials including air-filled cavities. Some preliminary numerical results are first
compared with the published analytical and experimental data to validate the proposed
modeling. Then, a developed design of anechoic using two arrays of air-filled bubbles is
considered. It is observed from the investigation results that the new coating shows an
interesting sound absorbing performance (i.e., absorbing > 80% incident energy in a large
frequency range 25 MHz) compared with the original one having a single air cavity array.
The developed structure allows broadening and tailoring their acoustic performance (peak
frequency and averaging level) by tuning some microstructural parameters of the air-filled
cavity (shape and size) and its distribution (location and fraction).

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
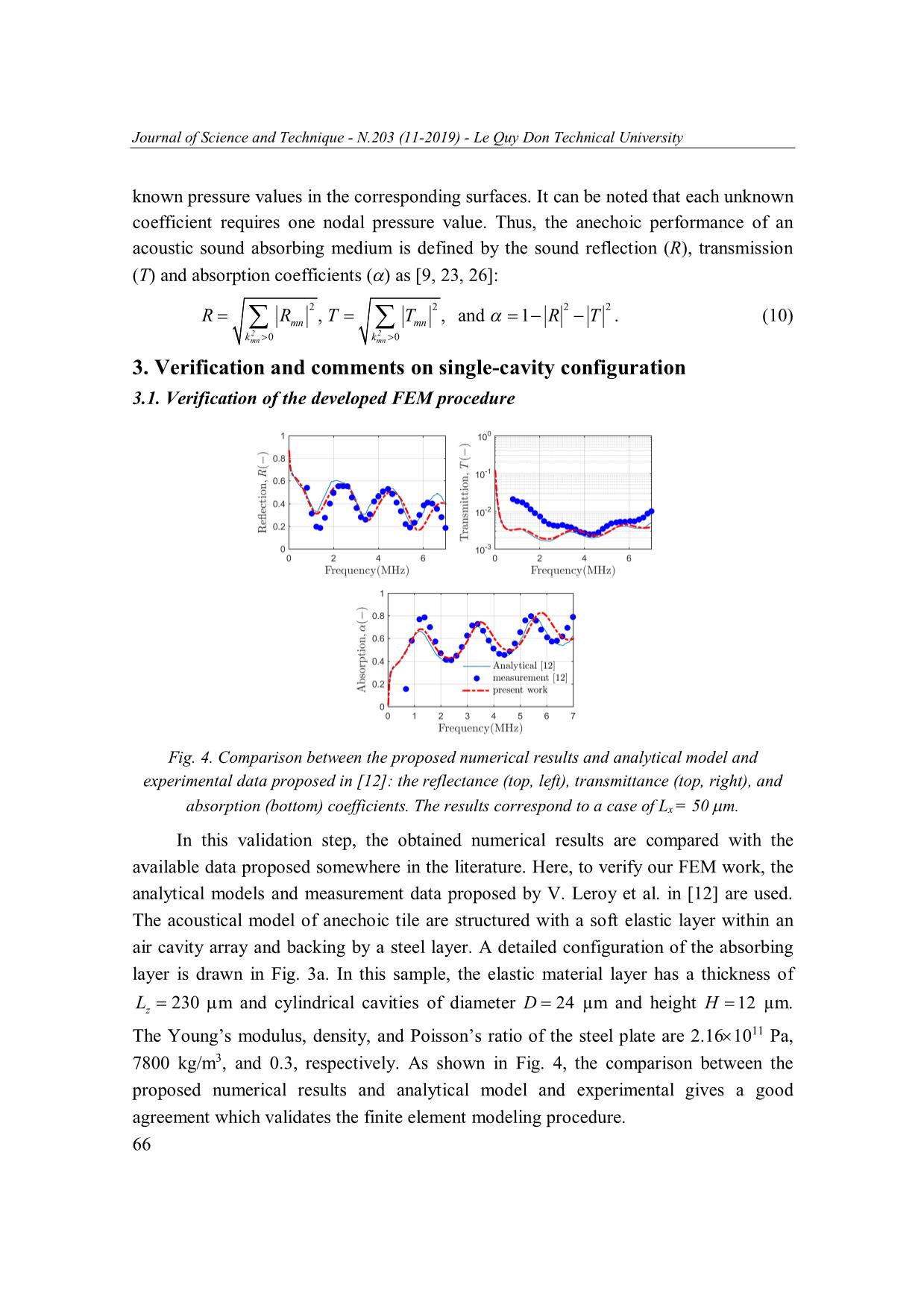
Trang 6
Trang 7

Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Numerical investigation of microstructure effect on acoustic properties of underwater anechoic coatings

Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University NUMERICAL INVESTIGATION OF MICROSTRUCTURE EFFECT ON ACOUSTIC PROPERTIES OF UNDERWATER ANECHOIC COATINGS Trinh Van Hai1*, Nguyen Van Tap2 1Le Quy Don Technical University 2Military Institute of Mechanical Engineering Abstract This paper presents a simulation-based model for predicting the acoustic properties of underwater anechoic structures with its main layer made of viscoelastic sound absorbing materials including air-filled cavities. Some preliminary numerical results are first compared with the published analytical and experimental data to validate the proposed modeling. Then, a developed design of anechoic using two arrays of air-filled bubbles is considered. It is observed from the investigation results that the new coating shows an interesting sound absorbing performance (i.e., absorbing > 80% incident energy in a large frequency range 25 MHz) compared with the original one having a single air cavity array. The developed structure allows broadening and tailoring their acoustic performance (peak frequency and averaging level) by tuning some microstructural parameters of the air-filled cavity (shape and size) and its distribution (location and fraction). Keywords: Air-filled cavity; acoustic property; anechoic coating; resonant sound absorber. 1. Introduction The high-quality acoustic stealth coatings are a complicated multi-scale and multi- component structure, by considering their microstructure, these anechoic structures can be categorized into three main types: air-filled cavity, multi-layer composite, pressure- resisting [1]. In such layered configurations, there are two types of resonance mechanisms which are due to either the radial motion of the hole wall or the drum-like oscillations of the cover layer [2]. Additionally, the developed structure allows us to broaden and tailor its acoustic performance by tuning some geometrical parameters of the air bubble distribution. It can be stated that macroscopic acoustic properties are highly dependent on the local microstructural features of each individual layer as well as the layer configuration [3]. Different approaches have been proposed in the literature to characterize the link between the microstructural parameter of anechoic structures and their macroscopic acoustic performance: analytical [4-7], numerical [8-11], and experimental methods * Email: hai.tv@lqdtu.edu.vn 61 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University [6, 12, 13]. Various analytical studies addressing scattering from gratings and resonant sound absorbers exist: transfer matrix method [14], effective medium model [15, 16], and cavity resonances mode [17, 18]. However, these analytical models often make simplifications on the displacement field and geometry, thereby imposing limitations on the type of problem to be solved. On the contrary, the numerical approach such as the finite element method (FEM) is more flexible in dealing with complex structures which allows analyzing harmonic wave propagation in viscoelastic gratings with periodic or random distributions with single- or multi-layer structures. As a survey introduced in [1], Russian designs enable to lower the noise level of Akula and Sierraz class submarines by 10~20 dB by anechoic coating using modified rubber. Britain technology has used polyurethane as anechoic material, lowering conventional submarine noise to 90 dB and meeting the qualifications of silent submarines. Furthermore, in US submarines, the double-layer anechoic structure composed of polyurethane and glass fibers can decrease noise by up to 40 dB and the radiated noise level of nuclear-powered submarines to less than 120 dB, approximately the ocean noise level (for more detailed about design and construction of US and Soviet submarines, see [19]). The remaining part of the paper is organized as follows. In Sec. 2, we first briefly introduce the theoretical background of acoustic aspects of wave propagation and the definitions of several acoustic properties used for characterizing sound absorbing structures. Then, we present a numerical framework at a relevant scale to implement the acoustical model of a multi-layer anechoic coating. Sec. 3 provides an example validation together an extended investigation about acoustical behavior of air-filled cavity anechoic structure with a single-cavity array in order to demonstrate the verification of the proposed numerical framework. In Sec. 4, a developed anechoic configuration and an analysis on its acoustical potential performance are proposed. Finally, some concluding remarks are given. 2. Theoretical formulation and numerical framework 2.1. Governing equations for structure-acoustic analysis The structure-acoustic problem is sketched sche ... sponding surfaces. It can be noted that each unknown coefficient requires one nodal pressure value. Thus, the anechoic performance of an acoustic sound absorbing medium is defined by the sound reflection (R), transmission (T) and absorption coefficients ( ) as [9, 23, 26]: 2 2 2 2 RRTTRT mn, mn , and 1 . (10) 2 2 kmn 0 k mn 0 3. Verification and comments on single-cavity configuration 3.1. Verification of the developed FEM procedure Fig. 4. Comparison between the proposed numerical results and analytical model and experimental data proposed in [12]: the reflectance (top, left), transmittance (top, right), and absorption (bottom) coefficients. The results correspond to a case of Lx = 50 m. In this validation step, the obtained numerical results are compared with the available data proposed somewhere in the literature. Here, to verify our FEM work, the analytical models and measurement data proposed by V. Leroy et al. in [12] are used. The acoustical model of anechoic tile are structured with a soft elastic layer within an air cavity array and backing by a steel layer. A detailed configuration of the absorbing layer is drawn in Fig. 3a. In this sample, the elastic material layer has a thickness of Lz 230 m and cylindrical cavities of diameter D 24 µm and height H 12 µm. The Young’s modulus, density, and Poisson’s ratio of the steel plate are 2.16 1011 Pa, 7800 kg/m3, and 0.3, respectively. As shown in Fig. 4, the comparison between the proposed numerical results and analytical model and experimental gives a good agreement which validates the finite element modeling procedure. 66 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 3.2. Tuning the fraction of air cavity Fig. 5. Acoustic performance of anechoic tiles with tuning air fraction. The results from top to bottom are respectively for the reflectance, transmittance and absorption coefficients In this section, we present how the distribution density of air cavity affects the acoustical behavior of the single air array anechoic. As demonstrated in [12], for the steel block alone, 88% of the energy is reflected and the remaining energy fraction (12%) is transmitted. Fig. 5 presents the energy proportions that are reflected (top), transmitted (middle) and absorbed (bottom) for various configurations of Lx (50 µm, 75 µm, 100 µm, 125 µm, and 150 µm). As expected, when the block is covered by the Lx = 120 µm meta-screen, the reflectance is drastically reduced (line with markers in Fig. 6 (top)), especially between 1.3 and 2.8 MHz where less than 6% of the incident energy is reflected, with the measured reflectance dropping nearly to zero at 1.3 MHz and 2.8 MHz. In terms of absorption (Fig. 6 (bottom)), all anechoic configurations manage to dissipate a significant part of the energy over a broad frequency range. Interestingly, the configuration with Lx = 100 µm (markers in Fig. 5 (bottom)) provides a very high absorption over the entire 1.32.8 MHz range, throughout which more than 91% of the incoming energy is dissipated, with a maximum absorbance of nearly 100% at 1.3 MHz and 2.8 MHz. The obtained trends here are in very good agreement with the suggested results illustrated in [12] for cases of Lx = 50 µm and Lx = 120 µm. 67 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 4. Results and discussion on double-cavity configuration 4.1. Design configuration Fig. 6. Configuration of viscoelastic absorbing layer with double void array. In this section, acoustical properties of anechoic tile with an absorbing panel of two lattice layers of air cylindrical cavities is investigated (Fig. 7). Compared to the original one, the geometric properties of the additional layer of voids are also introduced by the d h cylindrical cavities with their distances Lx and Ly in the x and y-direction, respectively, at the location l within the elastic layer. The potential acoustical performance of this developed coating structure is demonstrated in the following part by tuning several structural parameters. Here, we focus only on the reflection and absorption property, for simplicity, the added air cavity is identical with the original one in terms of shape (d = D, h = H) and distributions (Lx and Ly). The effect of the configuration difference between two air layers on its acoustical properties will be characterized in the forthcoming works. 4.2. Cylindrical cavity size effect (D) Fig. 7 shows the performance of anechoic tile based on air cavity having H = 13 m, Lx = Ly = 100 m, l = Lx/4, and varying its diameter D from 10 m to 25 m. It is observed that by the acoustical behavior of the double air array coating depends strongly on the air-filled cavity diameter. The anechoic within small void seems to have good acoustical behavior at low frequencies nearly 1.6 MHz (see the shape peak in Fig. 7 with more than 96% of the incoming energy is absorbed while remaining less than 3% reflected energy). Interestingly, compared with the results demonstrated in Fig. 5 with 24-diameter air cavities, the double array configuration (with D = 15 m and D = 20 m representing respectively by thin dashed and thick solid line) can provide a good acoustical functional factors ( 94.5%) at high frequency range (4 5 MHz). 68 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University Fig. 7. Effects of the cylindrical cavity size on acoustical performance of anechoic tiles: reflection (left) and absorption (right). 4.3. Air cavity density effect (Lx) Fig. 8. Effects of the air cavity distribution on acoustical performance of anechoic tiles: reflection (left) and absorption (right). In order to show the effect of the air-filled cavity density, this section investigates anechoic tile based on air cavity having H = 13 m, D = 24 m, l = 100 m, and varying cavity distance from 50 m to 125 m. It can be seen from the results from Fig. 8 that the length Lx affects both in the level of reflected and absorbed energy and the frequency occurring the second shape peak. In detail, the absorption property increases monotonically when Lx increases for Lx < 100 m and then decreases monotonically when Lx continues to increase above the critical value Lx = 100 m. Generally, the air cavity with length around 100 m shows good acoustical performance (see the thick solid line). 4.4. Cavity array distance effect (l) The third parameter of anechoic tile is the distance between two cavity layers l (50 m, 100 m, 150 m and 250 m). Here, the remaining parameters are kept as: 69 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University D = 24 m, H = 13 m, and Lx = Ly = 100 m. From the Fig. 9, it is seen that both fluctuations of reflection and absorption property are related fully to the air cavity distance. Within the distance l ranging from 50 m to 250 m, we enable to tailor the number of shape peaks and the fluctuated amplitude of acoustic performance. It should finally be noticed that the configuration with l = 150 m provides a good absorption (>80% of the incident energy, see the thick solid line) in the frequency range 25 MHz. Fig. 9. Effects of the cavity distance on acoustical performance of anechoic tiles: reflection (left) and absorption (right). 5. Conclusions In this paper, the simulation-based approach is presented to investigate the link between microstructure and acoustic properties of an anechoic structure with periodic air cavities. To this regard, the multi-layer anechoic coating is reconstructed, and the acoustic-structure model is generated including a cover layer, a viscoelastic absorbing panel and the steel layer as the backing. From this, the reflection, absorption, and transmission properties of the anechoic coating backing a steel plate are calculated numerically. Very good agreements are observed between the present numerical results of and an anechoic layer within a single cavity array with the analytical model, numerical results, and experimental data from the literature, which validates the suggested simulation-based procedure. From investigated results of the developed configuration, it is seen that all tuning geometrical parameters of the added air cavity affect strongly the acoustical properties. The air cavity size and its density have an effect on the level of reflected and absorbed energy, whereas the air cavity distance has only effect on the fluctuating behavior. This interesting point shows a good opportunity to achieve a desired reflection or absorption properties in an entire frequency range by tuning together all three parameters mentioned here and also others fixed (e.g., thickness layer L, ratios d/D, h/H). 70 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University References 1. Qian, C. and Y. Li (2017). Review on Multi-scale Structural Design of Submarine Stealth Composite. DEStech Transactions on Engineering and Technology Research. (icaenm). 2. Gaunaurd, G. (1985). Comments on ‘Absorption mechanisms for waterborne sound in Alberich anechoic layers’. Ultrasonics, 23(2), pp. 90-91. 3. Yang, M. and P. Sheng (2017). Sound absorption structures: From porous media to acoustic metamaterials. Annual Review of Materials Research, 47, pp. 83-114. 4. Gaunaurd, G. (1977). One‐dimensional model for acoustic absorption in a viscoelastic medium containing short cylindrical cavities. The Journal of the Acoustical Society of America, 62(2), pp. 298-307. 5. Meng, T., (2014). Simplified model for predicting acoustic performance of an underwater sound absorption coating. Journal of Vibration and Control, 20(3), pp. 339-354. 6. Leroy, V., et al. (2009). Transmission of ultrasound through a single layer of bubbles. The European Physical Journal E, 29(1), pp. 123-130. 7. Sharma, G.S., et al. (2017). Acoustic performance of gratings of cylindrical voids in a soft elastic medium with a steel backing. The Journal of the Acoustical Society of America, 141(6), pp. 4694-4704. 8. Ma, T.-C., R. Scott, and W.H. Yang (1980). Harmonic wave propagation in an infinite elastic medium with a periodic array of cylindrical pores. Journal of Sound and Vibration, 71(4), pp. 473-482. 9. Hladky‐Hennion, A.C. and J.N. Decarpigny (1991). Analysis of the scattering of a plane acoustic wave by a doubly periodic structure using the finite element method: Application to Alberich anechoic coatings. The Journal of the Acoustical Society of America, 90(6), pp. 3356-3367. 10. Sohrabi, S.H. and M.J. Ketabdari (2018). Numerical simulation of a viscoelastic sound absorbent coating with a doubly periodic array of cavities. Cogent Engineering, 5(1), pp. 1-21. 11. Zhong, J., et al. (2019). On the accuracy and optimization application of an axisymmetric simplified model for underwater sound absorption of anechoic coatings. Applied Acoustics, 145, pp. 104-111. 12. Leroy, V., et al. (2015). Superabsorption of acoustic waves with bubble metascreens. Physical Review, B 91(2), 020301. 13. Leroy, V., et al. (2009). Design and characterization of bubble phononic crystals. Applied Physics Letters, 95(17), p. 171904. 14. Sastry, J. and M. Munjal (1995). A transfer matrix approach for evaluation of the response of a multi-layer infinite plate to a two-dimensional pressure excitation. Journal of sound and vibration, 182(1), pp. 109-128. 15. Gaunaurd, G. and W. Wertman (1989). Comparison of effective medium theories for inhomogeneous continua. The Journal of the Acoustical Society of America, 85(2), pp. 541-554. 16. Bai, D. and J.B. Keller (1987). Sound waves in a periodic medium containing rigid spheres. The Journal of the Acoustical Society of America, 82(4), pp. 1436-1441. 71 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 17. Ivansson, S.M. (2012). Anechoic coatings obtained from two-and three-dimensional monopole resonance diffraction gratings. The Journal of the Acoustical Society of America, 131(4), pp. 2622-2637. 18. Ivansson, S.M. (2006). Sound absorption by viscoelastic coatings with periodically distributed cavities. The Journal of the Acoustical Society of America, 119(6), pp. 3558-3567. 19. Polmar, N. and K.J. Moore (2004). Cold War submarines: the design and construction of US and Soviet submarines. Potomac Books, Inc. 20. Zhang, Z. and X. Han (2016). A new hybrid phononic crystal in low frequencies. Physics Letters A, 380(45): p. 3766-3772. 21. Achenbach, J. (2012). Wave propagation in elastic solids, 16. Elsevier. 22. Sandberg, G., P.-A. Wernberg, and P. Davidsson (2008). Fundamentals of fluid-structure interaction. Computational aspects of structural acoustics and vibration. Springer, pp. 23-101. 23. Fu, X., et al. (2015). Sound absorption of a rib-stiffened plate covered by anechoic coatings. The Journal of the Acoustical Society of America, 137(3), pp. 1551-1556. 24. Hopkins, C. (2012). Sound insulation. Routledge. 25. Easwaran, V. and M. Munjal (1993). Analysis of reflection characteristics of a normal incidence plane wave on resonant sound absorbers: A finite element approach. The Journal of the Acoustical Society of America, 93(3), pp. 1308-1318. 26. Wen, J., et al. (2011). Effects of locally resonant modes on underwater sound absorption in viscoelastic materials. The Journal of the Acoustical Society of America, 130(3), pp. 1201-1208. KHẢO SÁT ẢNH HƯỞNG CỦA CẤU TRÚC VI MÔ ĐẾN ĐẶC TÍNH ÂM CỦA LỚP KHÔNG PHẢN XẠ DƯỚI NƯỚC Tóm tắt: Bài báo này trình bày mô hình dựa trên mô phỏng số để dự đoán tính chất âm học của cấu trúc không phản xạ dưới nước với lớp chính được làm bằng vật liệu hấp thụ âm có cấu tạo gồm các khoang khí. Một số kết quả số trước tiên được so sánh với kết quả giải tích và dữ liệu thực nghiệm đã công bố để kiểm chứng mô hình đề xuất. Sau đó, tiến hành xem xét thiết kế mới cấu trúc ngói sử dụng hai lớp khoang khí. Theo kết quả khảo sát nhận được, lớp ngói không phản xạ mới cho hiệu quả hấp thụ âm thanh tốt hơn (chẳng hạn hấp thụ hơn 80% năng lượng sóng tới trên dải tần rộng từ 2 đến 5 MHz) so với cấu hình gốc chỉ có một lớp khoang khí duy nhất. Ngoài ra, cấu trúc phát triển cho phép mở rộng và điều chỉnh hiệu quả âm (tần số đạt khả năng hấp thụ cao cũng như mức độ hấp thụ trung bình) bằng cách điều chỉnh một số thông số hình học (hình dáng và kích thước) và phân bố (vị trí và mật độ) của khoang khí. Từ khóa: Khoang khí; đặc tính âm; lớp không phản xạ; hấp thụ âm cộng hưởng. Received: 02/4/2019; Revised: 18/11/2019; Accepted for publication: 22/11/2019 72
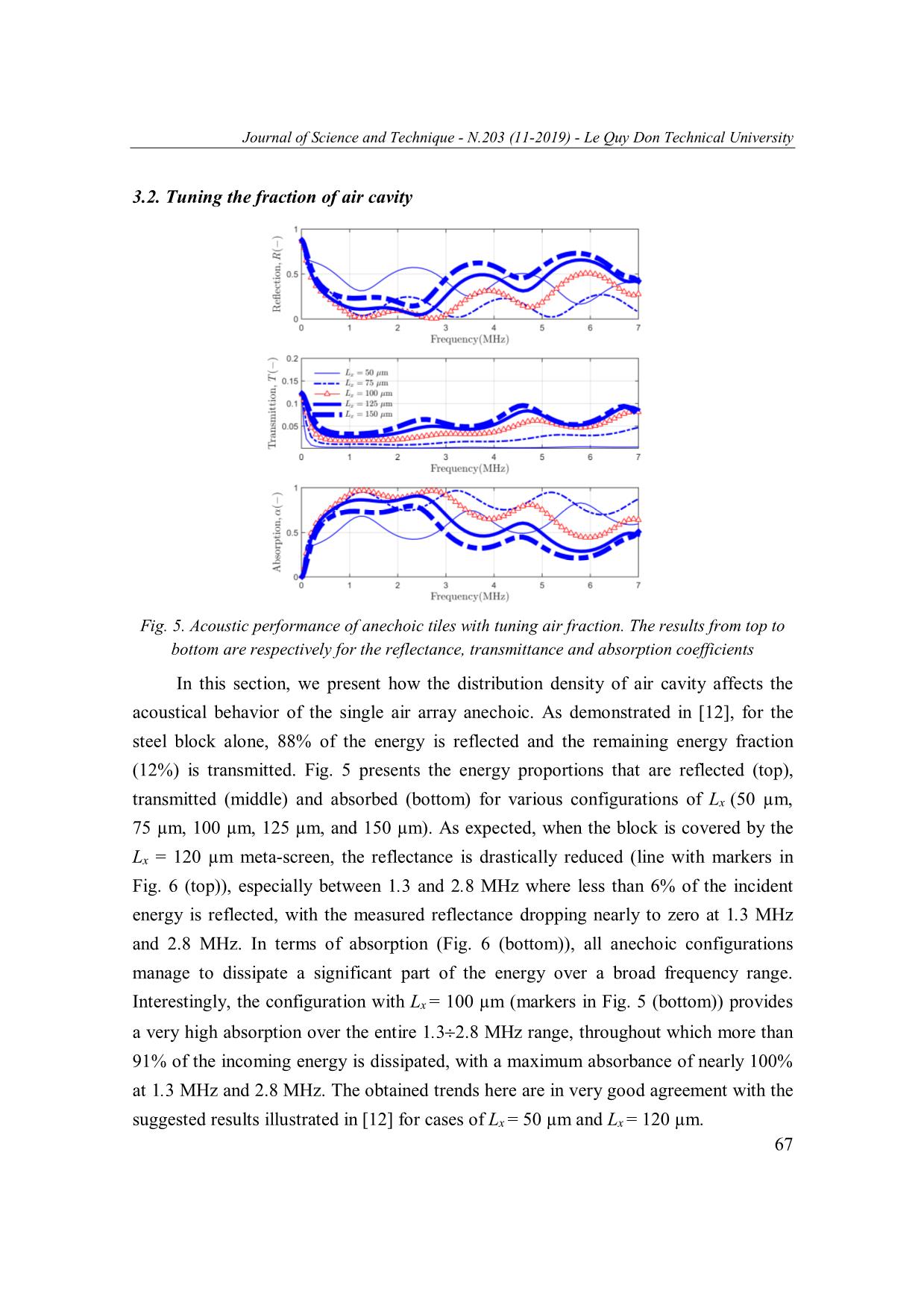
File đính kèm:
 numerical_investigation_of_microstructure_effect_on_acoustic.pdf
numerical_investigation_of_microstructure_effect_on_acoustic.pdf

