Numerical investigation of force transmission in granular media using discrete element method
Abstract. In this paper, a numerical Discrete Element Method (DEM) model was calibrated to investigate the transmission of force in granular media. To this aim, DEM simulation was performed for reproducing the behavior of a given granular material under
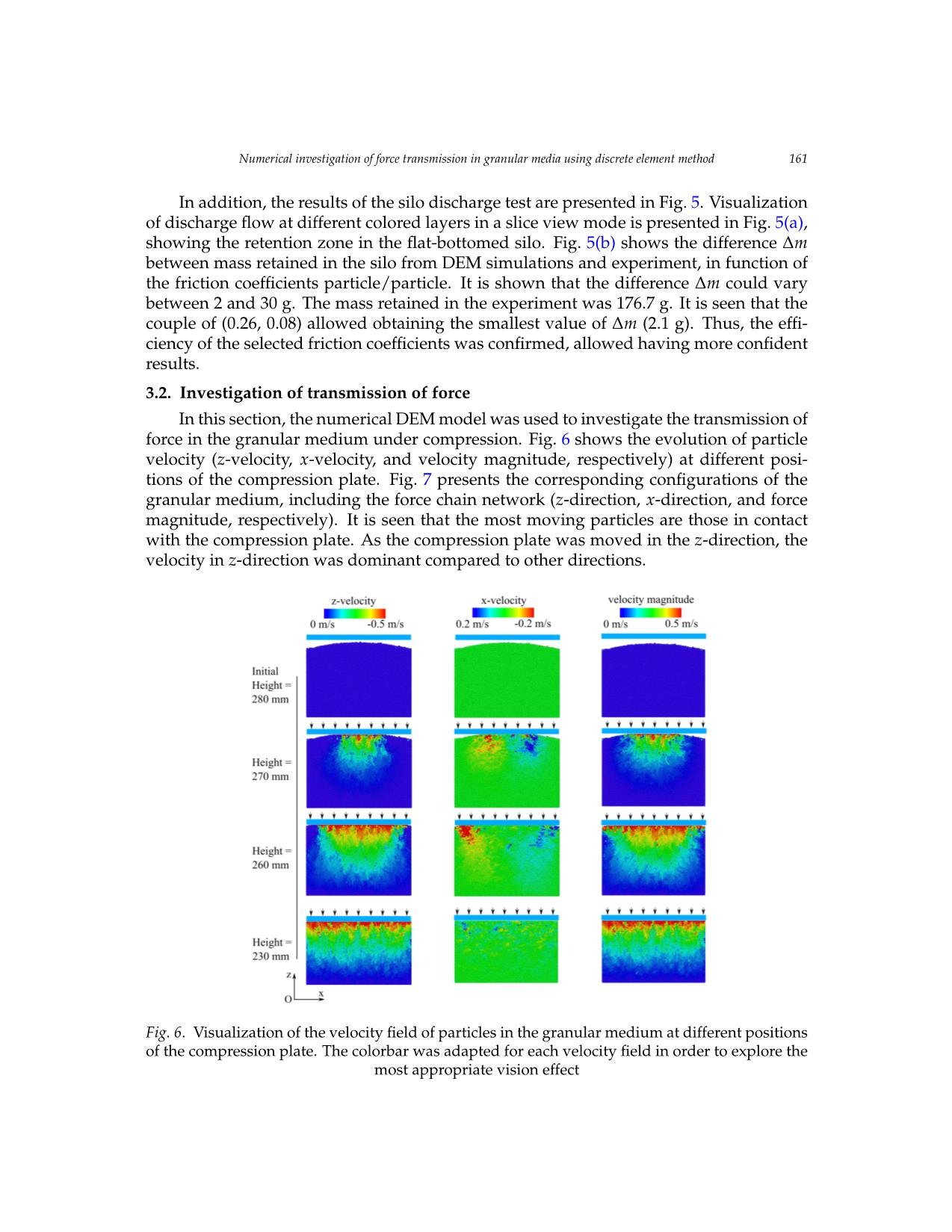
uniform compression. The DEM model was validated by comparing the obtained shear
stress/normal stress ratio with results published in the available literature. The network
of contact forces was then computed, showing the arrangement of the material microstructure under applied loading. The number and distribution of the contacts force were also
examined statistically, showing that the macroscopic behavior of the granular medium
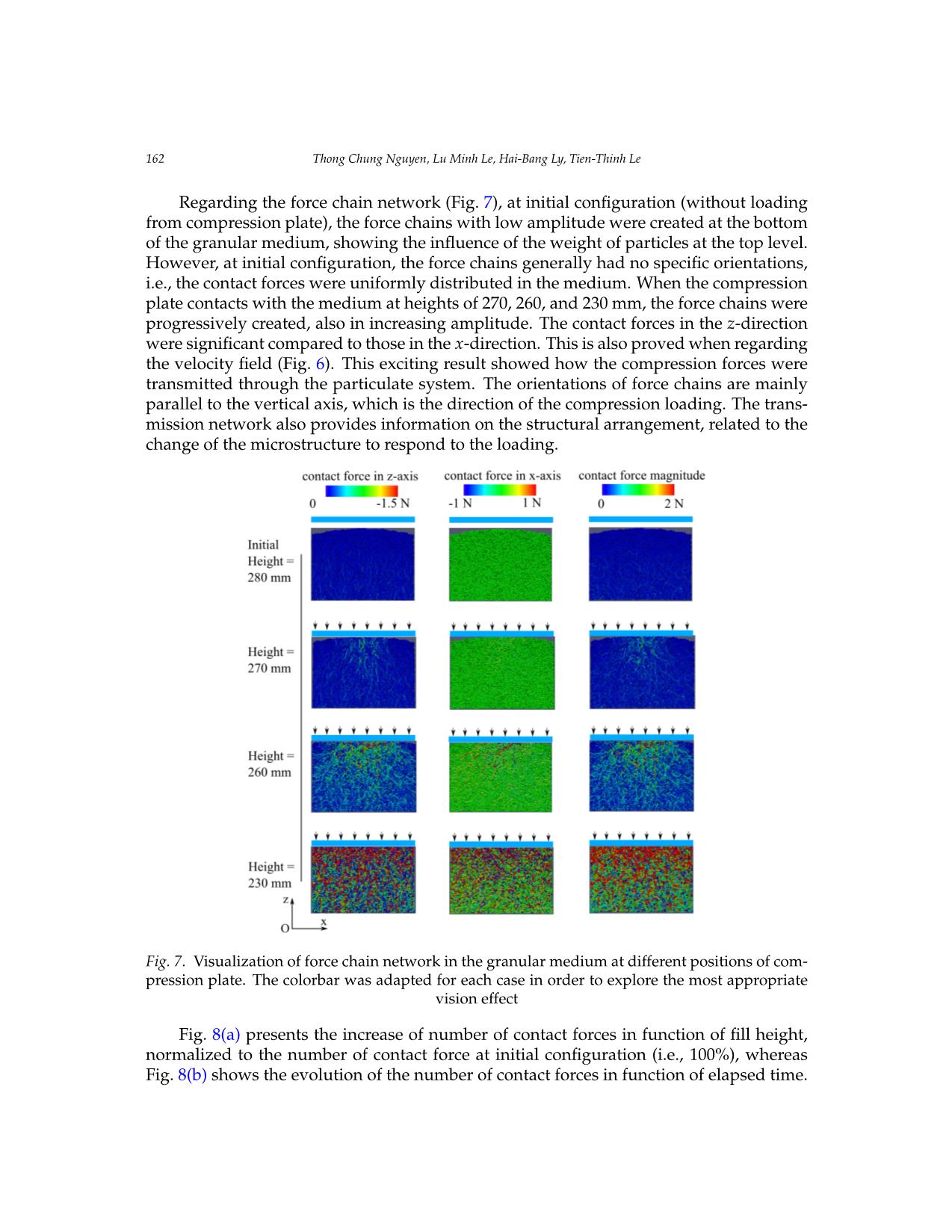
highly depended on the force chain network. The DEM model could be useful in exploring the mechanical response of granular materials under different loadings and boundary
conditions.
Keywords: granular mechanics, discrete element method, force chain, compression test.

Trang 1

Trang 2

Trang 3
Trang 4
Trang 5
Trang 6
Trang 7
Trang 8
Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Numerical investigation of force transmission in granular media using discrete element method

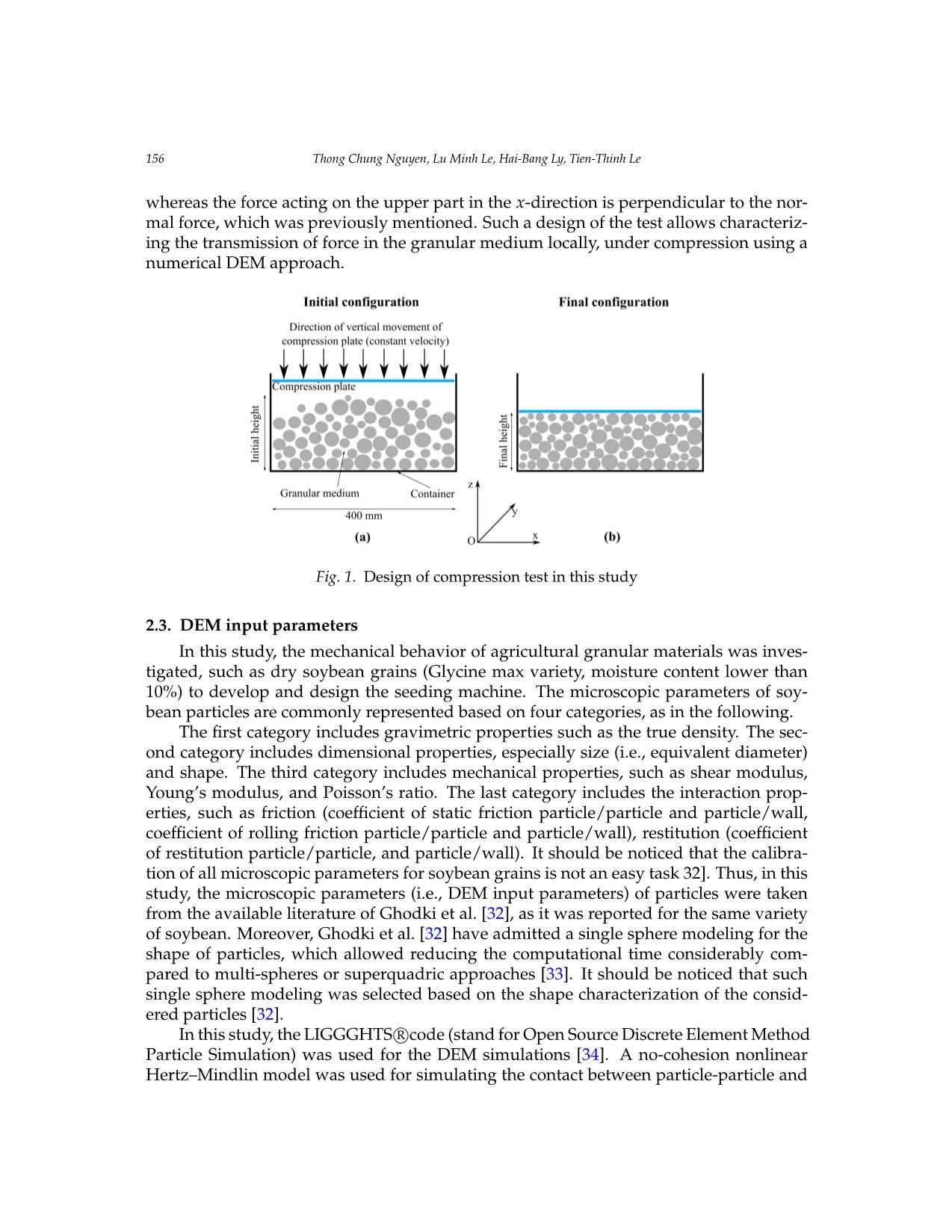
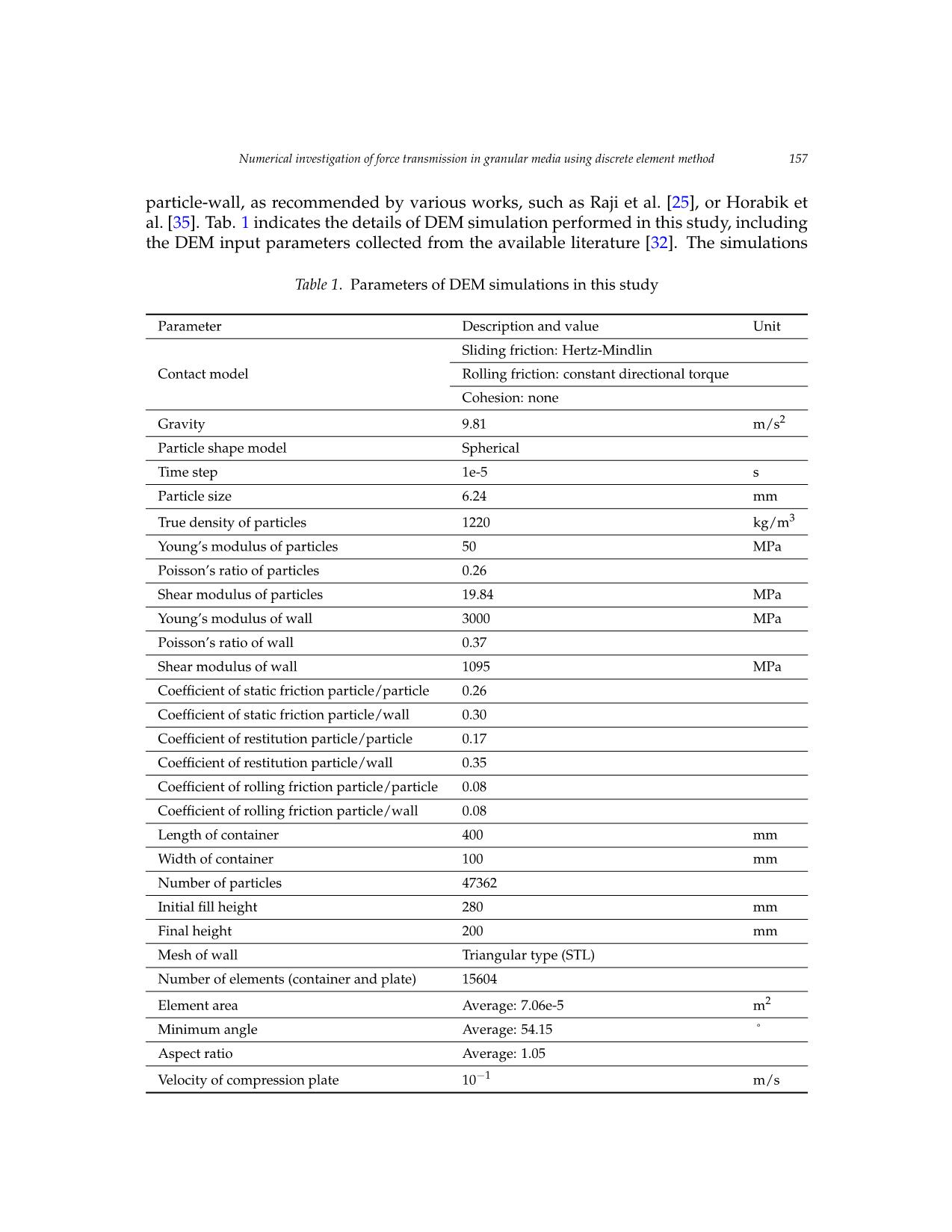
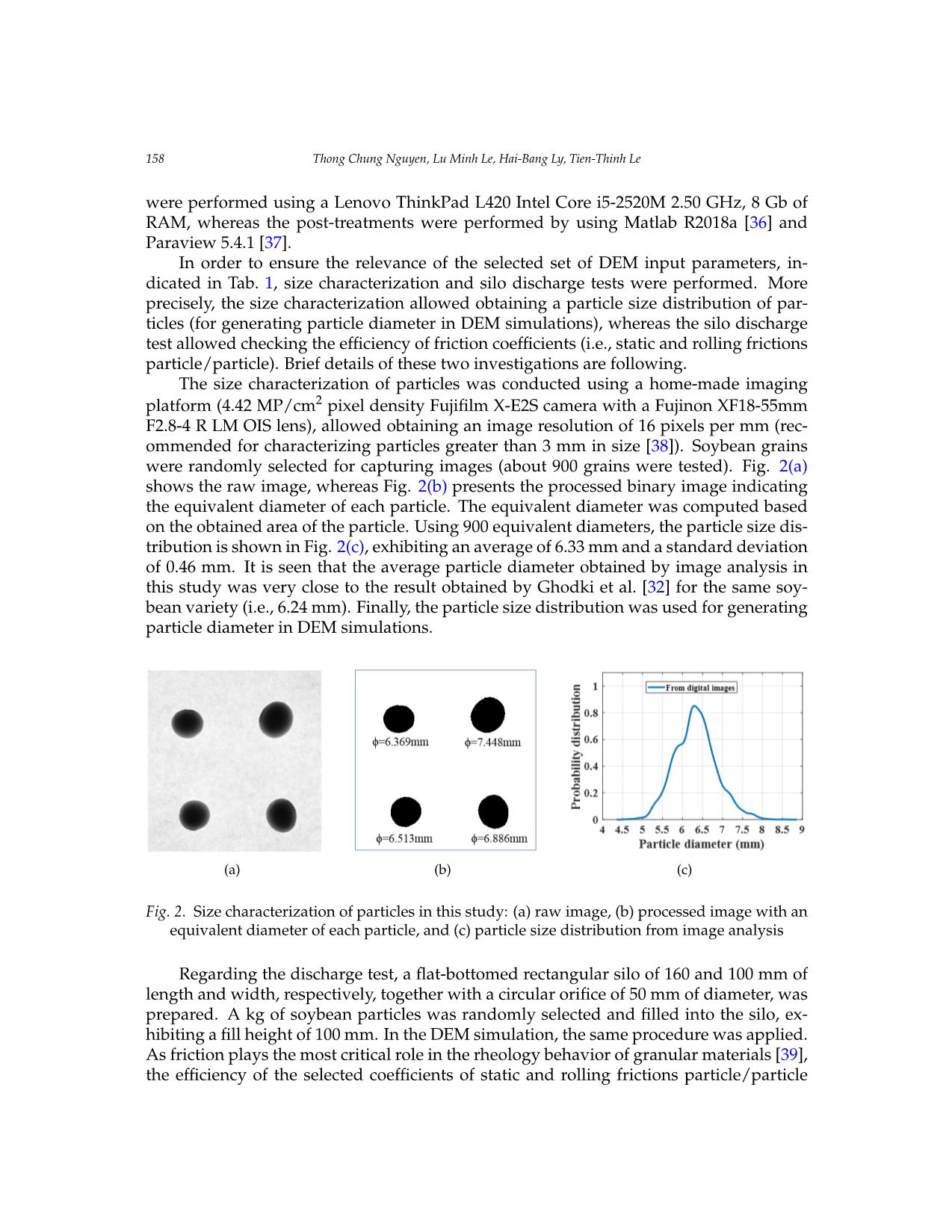
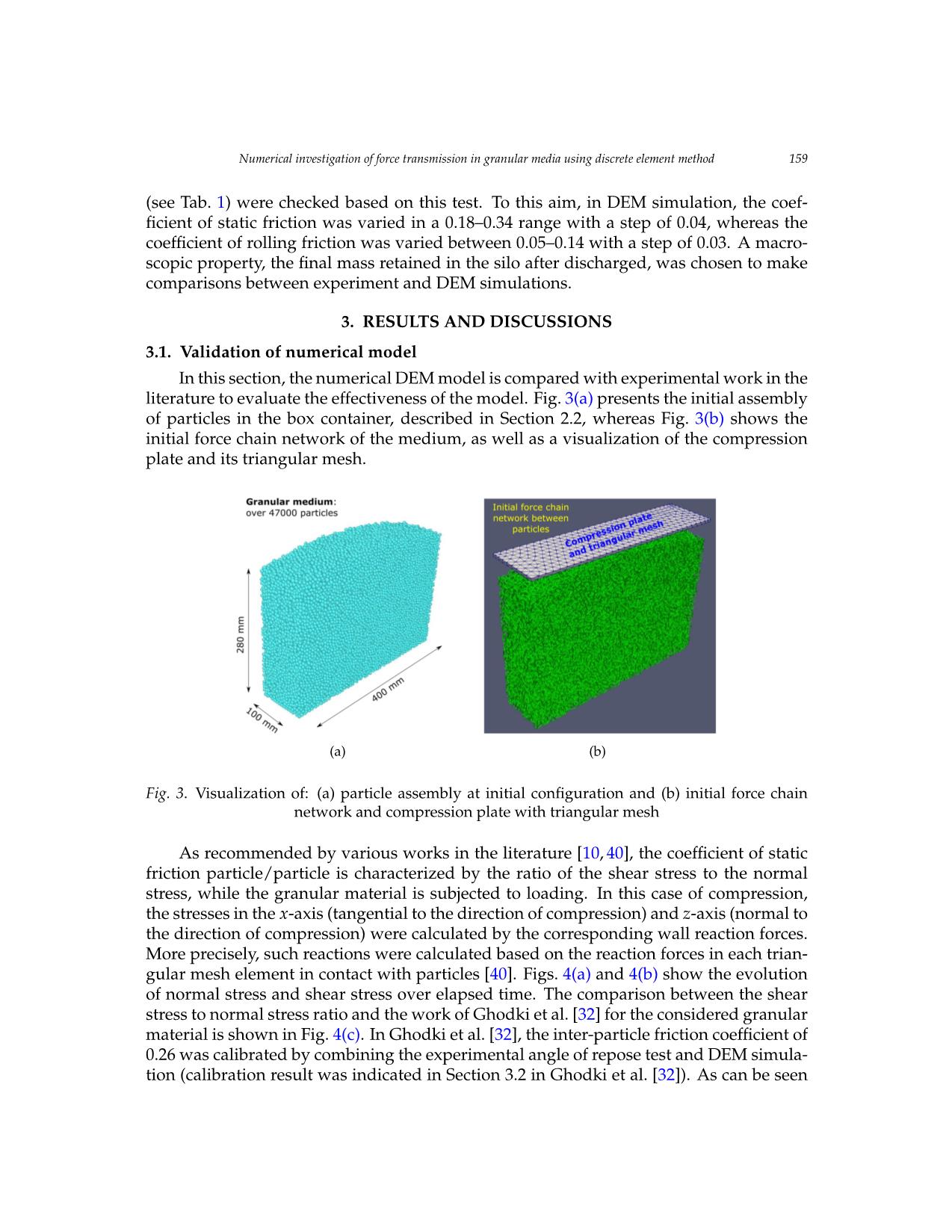
Vietnam Journal of Mechanics, VAST, Vol.42, No. 2 (2020), pp. 153 – 171 DOI: https://doi.org/10.15625/0866-7136/14787 NUMERICAL INVESTIGATION OF FORCE TRANSMISSION IN GRANULAR MEDIA USING DISCRETE ELEMENT METHOD Thong Chung Nguyen1, Lu Minh Le1, Hai-Bang Ly2, Tien-Thinh Le3,∗ 1Vietnam National University of Agriculture, Hanoi, Vietnam 2University of Transport Technology, Hanoi, Vietnam 3Duy Tan University, Da Nang, Vietnam ∗E-mail: letienthinh@duytan.edu.vn Received: 19 January 2020 / Published online: 10 May 2020 Abstract. In this paper, a numerical Discrete Element Method (DEM) model was cali- brated to investigate the transmission of force in granular media. To this aim, DEM sim- ulation was performed for reproducing the behavior of a given granular material under uniform compression. The DEM model was validated by comparing the obtained shear stress/normal stress ratio with results published in the available literature. The network of contact forces was then computed, showing the arrangement of the material microstruc- ture under applied loading. The number and distribution of the contacts force were also examined statistically, showing that the macroscopic behavior of the granular medium highly depended on the force chain network. The DEM model could be useful in explor- ing the mechanical response of granular materials under different loadings and boundary conditions. Keywords: granular mechanics, discrete element method, force chain, compression test. 1. INTRODUCTION A granular medium is composed of separate particles that move without depen- dence and interact with other particles via contact points [1]. Typical granular materials could be found in civil engineering, such as geotechnical engineering, mining or energy production, chemical, pharmaceutical, and agricultural industries [2–4]. Research and development of machinery/device for processing granular materials have been consid- erably increased over the past ten years, requiring above all a good knowledge of inter- actions between particulate systems itself and with machine parts [5]. For instance, the coefficient of friction has been introduced, measured to characterize the dissipation of en- ergy when the particles collide [6]. These particulate interactions have been investigated for many years using analytical, semi-analytical, or experimental approaches [3,7,8]. De- spite all the efforts, it is not always possible to carry out a large number of configurations c 2020 Vietnam Academy of Science and Technology 154 Thong Chung Nguyen, Lu Minh Le, Hai-Bang Ly, Tien-Thinh Le taking into account all the possible parameters [6]. Moreover, experimental works might not have the required ability to investigate the local interactions, particularly in terms of transmission of stress, collapse of force chain under deformation and so on [9]. It clearly showed that a more robust manner is thus required for better understanding and charac- terizing the mechanical properties of granular materials [10]. From a numerical simulation point of view, the mechanics of granular media can be modeled by either continuum [11–13] or discrete [14–16] approaches. More precisely, in a discrete approach, the Discrete Element Method (DEM) has been primarily employed to simulate granular materials [10, 17]. As an example, Than et al. [18] have developed a DEM model for investigating the plastic response of wet granular material under com- pression. Also, based on DEM technique, Xie et al. [19] have pointed out the influence of interlayer on the strength and deformation of layered rock specimens in uniaxial tests. In another study, Tran et al. [2] have employed DEM algorithm to simulate the behavior of concrete under triaxial loading. Xu et al. [20] have proposed a comparison between DEM simulation and experiments while investigating the mechanical behavior of sea ice. Lom- men et al. [17] have studied the relationship between particle stiffness and bulk material behavior in a numerical simulation context. Furthermore, the combination of DEM and other numerical techniques has been performed by Dratt and Katterfeld [21]. The authors have combined DEM with Finite Element Method (FEM) for investigating the dynamic deformation of machine parts in contact with particle flow. Besides, Zhou et al. [22] have combined DEM with Computational Fluid Dynamics (CFD) for modeling granular flow in hydraulic conveyor. So far, studies involving DEM technique could strongly improve the investigation of mechanical properties of particulate systems by enabling an access to the local behavior in a granular media. Such numerical simulation technique could also save time and cost compared with complex experiments in the design and development of machinery involving particulate systems. In this study, DEM model was developed for investigating the transmission of stress in granular media under the compression forc ... sation towards continuum quantities. PAMM, 13, (1), (2013), pp. 575–576. https://doi.org/10.1002/pamm.201310269. [14] M. Tolomeo, V. Richefeu, G. Combe, J. N. Roux, and G. Viggiani. An assessment of discrete element approaches to infer intergranular forces from experiments on 2D granular media. International Journal of Solids and Structures, 187, (2020), pp. 48–57. https://doi.org/10.1016/j.ijsolstr.2019.01.010. [15] J. Duriez and R. Wan. Stress in wet granular media with interfaces via homogeniza- tion and discrete element approaches. Journal of Engineering Mechanics, 142, (12), (2016). https://doi.org/10.1061/(asce)em.1943-7889.0001163. [16] M. Servin, D. Wang, C. Lacoursiere,` and K. Bodin. Examining the smooth and nonsmooth discrete element approaches to granular matter. International Journal for Numerical Methods in Engineering, 97, (12), (2014), pp. 878–902. https://doi.org/10.1002/nme.4612. [17] S. Lommen, D. Schott, and G. Lodewijks. DEM speedup: Stiffness effects on behavior of bulk material. Particuology, 12, (2014), pp. 107–112. https://doi.org/10.1016/j.partic.2013.03.006. [18] V. D. Than, S. Khamseh, A. M. Tang, J.-M. Pereira, F. Chevoir, and J.-N. Roux. Basic mechan- ical properties of wet granular materials: a DEM study. Journal of Engineering Mechanics, 143, (1), (2017). https://doi.org/10.1061/(asce)em.1943-7889.0001043. [19] L. Xie, P. Jin, T.-C. Su, X. Li, and Z. Liang. Numerical simulation of uniaxial compression tests on layered rock specimens using the discrete element method. Computational Particle Mechanics, (2019), pp. 1–10. https://doi.org/10.1007/s40571-019-00307-3. [20] Z. Xu, A. M. Tartakovsky, and W. Pan. Discrete-element model for the in- teraction between ocean waves and sea ice. Physical Review E, 85, (1), (2012). https://doi.org/10.1103/physreve.85.016703. [21] M. Dratt and A. Katterfeld. Coupling of FEM and DEM simulations to con- sider dynamic deformations under particle load. Granular Matter, 19, (3), (2017). https://doi.org/10.1007/s10035-017-0728-3. [22] M. Zhou, S. Wang, S. Kuang, K. Luo, J. Fan, and A. Yu. CFD-DEM modelling of hydraulic conveying of solid particles in a vertical pipe. Powder Technology, 354, (2019), pp. 893–905. https://doi.org/10.1016/j.powtec.2019.07.015. [23] M. Kobayakawa, S. Miyai, T. Tsuji, and T. Tanaka. Interaction between dry gran- ular materials and an inclined plate (comparison between large-scale DEM sim- ulation and three-dimensional wedge model). Journal of Terramechanics, (2019). https://doi.org/10.1016/j.jterra.2019.08.006. [24] C. Gonzalez-Montellano,´ J. M. Fuentes, E. Ayuga-Tellez,´ and F. Ayuga. Determi- nation of the mechanical properties of maize grains and olives required for use in DEM simulations. Journal of Food Engineering, 111, (4), (2012), pp. 553–562. https://doi.org/10.1016/j.jfoodeng.2012.03.017. Numerical investigation of force transmission in granular media using discrete element method 169 [25] A. O. Raji and J. F. Favier. Model for the deformation in agricultural and food particu- late materials under bulk compressive loading using discrete element method. I: Theory, model development and validation. Journal of Food Engineering, 64, (3), (2004), pp. 359–371. https://doi.org/10.1016/j.jfoodeng.2003.11.004. [26] V.-T. Nguyen and M.-Q. Le. Atomistic simulation of the uniaxial compression of black phosphorene nanotubes. Vietnam Journal of Mechanics, 40, (3), (2018), pp. 243–250. https://doi.org/10.15625/0866-7136/10982. [27] K. L. Johnson, K. Kendall, and a. Roberts. Surface energy and the contact of elastic solids. In Proceedings of the Royal Society of London. Series A. Mathematical and Physical Sciences, The Royal Society London, Vol. 324, (1971), pp. 301–313, https://doi.org/10.1098/rspa.1971.0141. [28] A. Di Renzo and F. P. Di Maio. Comparison of contact-force models for the simulation of collisions in DEM-based granular flow codes. Chemical Engineering Science, 59, (3), (2004), pp. 525–541. https://doi.org/10.1016/j.ces.2003.09.037. [29] K. F. Malone and B. H. Xu. Determination of contact parameters for discrete ele- ment method simulations of granular systems. Particuology, 6, (6), (2008), pp. 521–528. https://doi.org/10.1016/j.partic.2008.07.012. [30] J. Ai, J.-F. Chen, J. M. Rotter, and J. Y. Ooi. Assessment of rolling resistance mod- els in discrete element simulations. Powder Technology, 206, (3), (2011), pp. 269–282. https://doi.org/10.1016/j.powtec.2010.09.030. [31] J. M. Boac, R. P. K. Ambrose, M. E. Casada, R. G. Maghirang, and D. E. Maier. Applications of discrete element method in modeling of grain postharvest operations. Food Engineering Reviews, 6, (4), (2014), pp. 128–149. https://doi.org/10.1007/s12393-014-9090-y. [32] B. M. Ghodki, M. Patel, R. Namdeo, and G. Carpenter. Calibration of discrete element model parameters: soybeans. Computational Particle Mechanics, 6, (1), (2019), pp. 3–10. https://doi.org/10.1007/s40571-018-0194-7. [33] T. Xu, J. Yu, Y. Yu, and Y. Wang. A modelling and verification approach for soybean seed particles using the discrete element method. Advanced Powder Technology, 29, (12), (2018), pp. 3274–3290. https://doi.org/10.1016/j.apt.2018.09.006. [34] C. Kloss, C. Goniva, A. Hager, S. Amberger, and S. Pirker. Models, algorithms and validation for opensource DEM and CFD–DEM. Progress in Computational Fluid Dynamics, an Interna- tional Journal, 12, (2-3), (2012), pp. 140–152. https://doi.org/10.1504/pcfd.2012.047457. [35] J. Horabik and M. Molenda. Parameters and contact models for DEM simulations of agri- cultural granular materials: A review. Biosystems Engineering, 147, (2016), pp. 206–225. https://doi.org/10.1016/j.biosystemseng.2016.02.017. [36] Matlab. Natick, MA, USA, (2018). The MathWorks. [37] U. Ayachit. The ParaView guide: A parallel visualization application, ParaView 4.3. Kitware, In- corporated, (2015). [38] D. O. C. Souza and F. C. Menegalli. Image analysis: Statistical study of particle size distribution and shape characterization. Powder Technology, 214, (1), (2011), pp. 57–63. https://doi.org/10.1016/j.powtec.2011.07.035. [39] C. J. Coetzee and D. N. J. Els. Calibration of granular material parameters for DEM modelling and numerical verification by blade–granular material interaction. Journal of Terramechanics, 46, (1), (2009), pp. 15–26. https://doi.org/10.1016/j.jterra.2008.12.004. [40] T. A. H. Simons, R. Weiler, S. Strege, S. Bensmann, M. Schilling, and A. Kwade. A ring shear tester as calibration experiment for DEM simulations in agitated mixers—a sensitivity study. Procedia Engineering, 102, (1), (2015), pp. 741–748. https://doi.org/10.1016/j.proeng.2015.01.178. 170 Thong Chung Nguyen, Lu Minh Le, Hai-Bang Ly, Tien-Thinh Le [41] W. Wu, G. Ma, W. Zhou, D. Wang, and X. Chang. Force transmission and anisotropic charac- teristics of sheared granular materials with rolling resistance. Granular Matter, 21, (4), (2019). https://doi.org/10.1007/s10035-019-0938-y. [42] A. Salazar, E. Saez,´ and G. Pardo. Modeling the direct shear test of a coarse sand using the 3D Discrete Element Method with a rolling friction model. Computers and Geotechnics, 67, (2015), pp. 83–93. https://doi.org/10.1016/j.compgeo.2015.02.017. [43] A. Tordesillas, C. A. H. Steer, and D. M. Walker. Force chain and contact cycle evolution in a dense granular material under shallow penetration. Nonlinear Processes in Geophysics, 21, (2), (2014), pp. 505–519. https://doi.org/10.5194/npg-21-505-2014. [44] T.-X. Xiu, W. Wang, K. Liu, Z.-Y. Wang, and D.-Z. Wei. Characteristics of force chains in fric- tional interface during abrasive flow machining based on discrete element method. Advances in Manufacturing, 6, (4), (2018), pp. 355–375. https://doi.org/10.1007/s40436-018-0236-7. [45] W. Wang, W. Gu, and K. Liu. Force chain evolution and force characteristics of shearing granular media in Taylor-Couette geometry by DEM. Tribology Transactions, 58, (2), (2015), pp. 197–206. https://doi.org/10.1080/10402004.2014.943829. [46] L. Zhang, N. G. H. Nguyen, S. Lambert, F. Nicot, F. Prunier, and I. Djeran- Maigre. The role of force chains in granular materials: from statics to dynamics. Eu- ropean Journal of Environmental and Civil Engineering, 21, (7-8), (2017), pp. 874–895. https://doi.org/10.1080/19648189.2016.1194332. Numerical investigation of force transmission in granular media using discrete element method 171 APPENDIX Critical breakage force In this work, the critical breakage force of soybean particles was measured using F.S. 20,000 kN testing machine, available at the Strength of materials laboratory, Faculty of En- gineering, Vietnam National University of Agriculture. In each test, three particles were positioned in the machine to form an equilateral triangle, as showing in Fig. A1(a). Three tests were finally conducted, as shown in Fig. A1(b) for displacement - compression force curves. The breakage of particles was observed at 50-70 N for most of the particles (i.e., a shortening higher than 1.5 mm compared to the average particle diameter of 6.24 mm). It should be noticed that the critical value should also be selected based on the germination 15 rate of particlesNguyen afterChung being Thong, deformed Le Minh (i.e., Lu, higher Ly Hai than Bang 85-90%). and Le Tien Consequently, Thinh 50 N was finally chosenNguyen as a critical Chung breakageThong, Le forceMinh Lu, of soybeanLy Hai Bang particles. and Le Tien Thinh 15 (a) (b) Fig. A1. Measurement of critical breakage force of particles: (a) compression test, (b) displacement - Fig.Fig. A1 A1. .Measurement Measurement of ofcritical critical breakage breakagecompression force force of ofparticles:force particles: curve. (a) (a)compression compression test, test, (b) (b)displacement displacement - compression- compression force force curve. curve REFERENCES [1] P.A. Cundall, O.D.L. Strack, A discrete numericalREFERENCES model for granular assemblies, Géotechnique. 29 (1979) 47–65. https://doi.org/10.1680/geot.1979.29.1.47. [1] P.A. Cundall, O.D.L. Strack, A discrete numerical model for granular assemblies, Géotechnique. 29 (1979) 47[2]– 65.V.T. https://doi.org/10.1680/geot.1979.29.1.47. Tran, F.-V. Donzé, P. Marin, A discrete element model of concrete under high triaxial loading, Cement and Concrete Composites. 33 (2011) 936–948. https://doi.org/10.1016/j.cemconcomp.2011.01.003. [2] V.T. Tran, F.-V. Donzé, P. Marin, A discrete element model of concrete under high triaxial loading, Cement [3] Z. Kaliniewicz, Z. Żuk, A relationship between friction plate roughness and the external friction angle of and Concretewheat Composites. kernels, International 33 (2011) 936 Journal–948. https://doi.org/10.1016/j.cemconco of Food Properties. 20 (2017)mp.2011.01.003. S2409–S2417. [3] Z. Kaliniewicz,https://doi.org/10.1080/10942912.2017.1371190. Z. Żuk, A relationship between friction plate roughness and the external friction angle of wheat[4] N.T. kernels, Cuong, B.H. International Ha, R. Fukagawa, Journal Failure mechanism of Food of two Properties.-dimensional granular 20 (2017) columns: Numerical S2409–S2417. https://doi.org/10.1080/10942912.2017.1371190.simulation and experiments, Vietnam Journal of Mechanics. 37 (2015) 239–250. https://doi.org/10.15625/0866-7136/37/4/5844. [4] N.T. Cuong, B.H. Ha, R. Fukagawa, Failure mechanism of two-dimensional granular columns: Numerical simulation[5] H. Fu, C. and Jin, J. Yu, experiments, The DEM- Based Vietnam Digital Design Journal Platform of for Agricultural Mechanics. Machinery 37 — (2015)AgriDEM, 239 in: –250. https://doi.org/10.15625/0866X. Li, Y. Feng, G. Mustoe-7136/37/4/5844. (Eds.), Proceedings of the 7th International Conference on Discrete Element Methods, Springer, Singapore, 2017: pp. 1253–1263. https://doi.org/10.1007/978-981-10-1926-5_129. [5] H.[6] Fu, J.C. Horabik, Jin, J. Yu, M. The Molenda, DEM - ForceBased and Digital contact Design area Platform of wheat for grain Agricultural in friction, Machinery Journal of — AgriculturalAgriDEM, in: X. Li, EngineeringY. Feng, G. Research. Mustoe 41 (Eds.), (1988) Proceedings33–42. https://doi.org/10.1016/0021 of the 7th International-8634(88)90201 Conference-6. on Discrete Element Methods, Springer, Singapore, 2017: pp. 1253–1263. https://doi.org/10.1007/978-981-10-1926-5_129. [7] E.P. Montellà, M. Toraldo, B. Chareyre, L. Sibille, Localized fluidization in granular materials: Theoretical [6] J. Horabik,and numerical M. Molenda, study, Phys. Force Rev. and E. 94 contact (2016) 052905. area of https://doi.org/10.1103/PhysRevE.94.052905. wheat grain in friction, Journal of Agricultural Engineering[8] D.T. Huan, Research. T.H. Quoc, 41 (1988) T.M. Tu,33– Free42. https://doi.org/10.1016/0021vibration analysis of functionally-8634(88)90201 graded shell panels-6. with various [7] E.P. Montellà,geometric M. shapes Toraldo, in B. thermal Chareyre, environment, L. Sibil le, Vietnam Localized Journal fluidization of Mechanics. in granular 40 materials: (2018) 199 Theoretical–215. https://doi.org/10.15625/0866-7136/10776. and numerical study, Phys. Rev. E. 94 (2016) 052905. https://doi.org/10.1103/PhysRevE.94.052905. [9] F. Nicot, H. Xiong, A. Wautier, J. Lerbet, F. Darve, Force chain collapse as grain column buckling in [8] D.T. Huan,granula T.H.r materials, Quoc, GranularT.M. Tu, Matter. Free 19vibration (2017) 18. analysis https://doi.org/10.1007/s10035 of functionally graded-017 shell-0702 panels-0. with various geometric shapes in thermal environment, Vietnam Journal of Mechanics. 40 (2018) 199–215. https://doi.org/10.15625/0866[10] Y. Zhou, H. Wang, B. Zhou,-7136/10776. J. Li, DEM- aided direct shear testing of granular sands incorporating realistic particle shape, Granular Matter. 20 (2018) 55. https://doi.org/10.1007/s10035-018-0828-8. [9] F.[11] Nicot, Z. Deng, H. Xiong, P.B. Umbanhowar, A. Wautier, J.M. J. Lerbet,Ottino, R.M. F. Darve, Lueptow, Force Continuum chain collapsemodelling as of grainsegregating column tridisperse buckling in granulagranularr materials, chute Granularflow, Proceedings Matter. of 19 the (2017) Royal Society18. https://doi.org/10.1007/s10035 A: Mathematical, Physical and Engineering-017-0702- 0.Sciences. 474 (2018) 20170384. https://doi.org/10.1098/rspa.2017.0384. [10] Y. Zhou, H. Wang, B. Zhou, J. Li, DEM-aided direct shear testing of granular sands incorporating realistic particle shape, Granular Matter. 20 (2018) 55. https://doi.org/10.1007/s10035-018-0828-8. [11] Z. Deng, P.B. Umbanhowar, J.M. Ottino, R.M. Lueptow, Continuum modelling of segregating tridisperse granular chute flow, Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 474 (2018) 20170384. https://doi.org/10.1098/rspa.2017.0384.
File đính kèm:
 numerical_investigation_of_force_transmission_in_granular_me.pdf
numerical_investigation_of_force_transmission_in_granular_me.pdf

