Một giải pháp dạy học tiết bài tập hỗ trợ học sinh yếu môn Toán (Chủ đề tìm tâm mặt cầu ngoại tiếp hình chóp)
Trong bài viết này, trước tiên, chúng tôi đề cập một số đặc điểm và nguyên nhân của học sinh (HS) yếu môn toán, sau đó đưa ra một giải pháp hỗ trợ HS thông qua bài toán gốc, từ bài toán gốc này đề xuất bài toán tương tự hoặc mở rộng bài toán giúp HS trong việc tìm tâm của mặt cầu ngoại tiếp hình chóp.

Trang 1

Trang 2

Trang 3

Trang 4
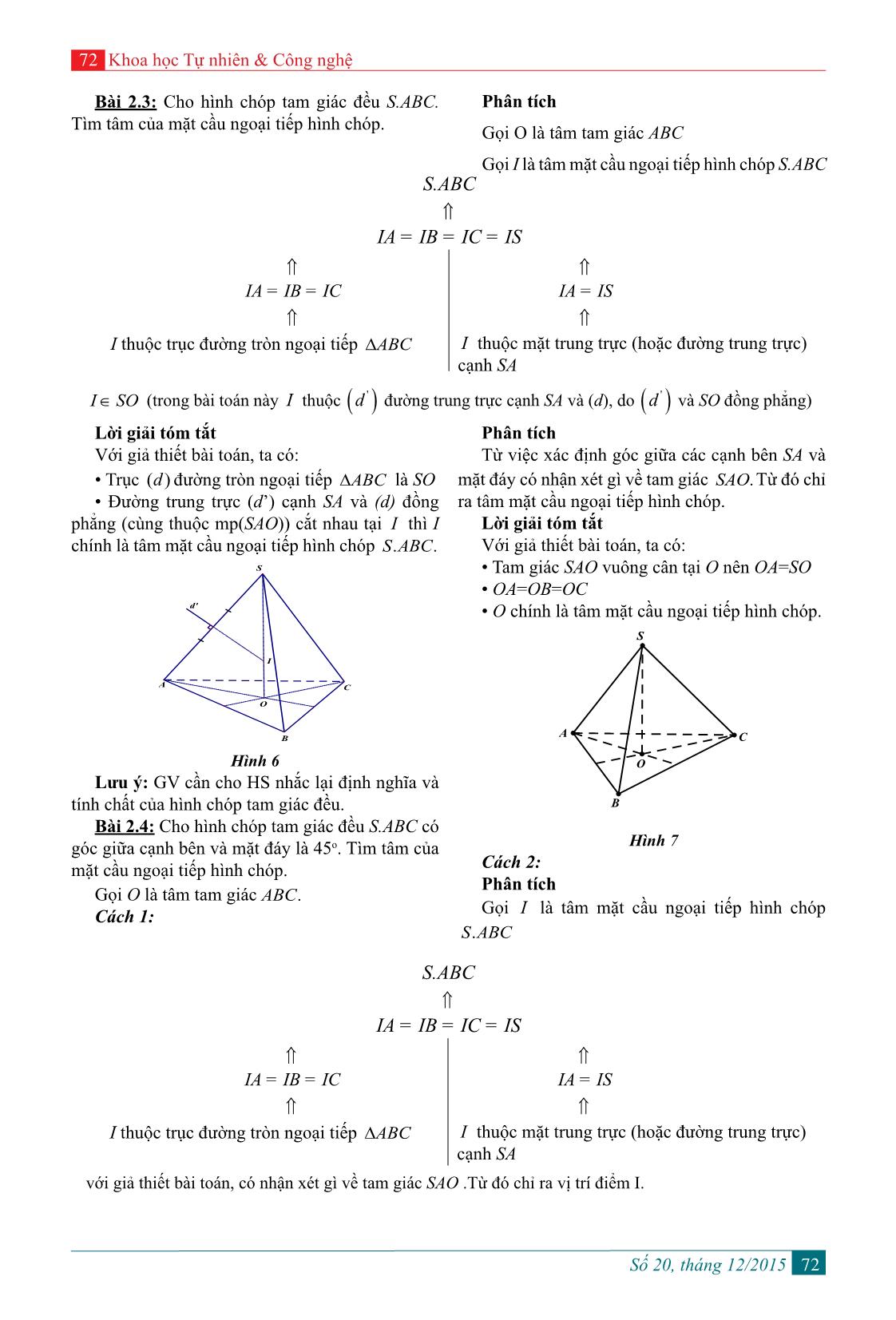
Trang 5
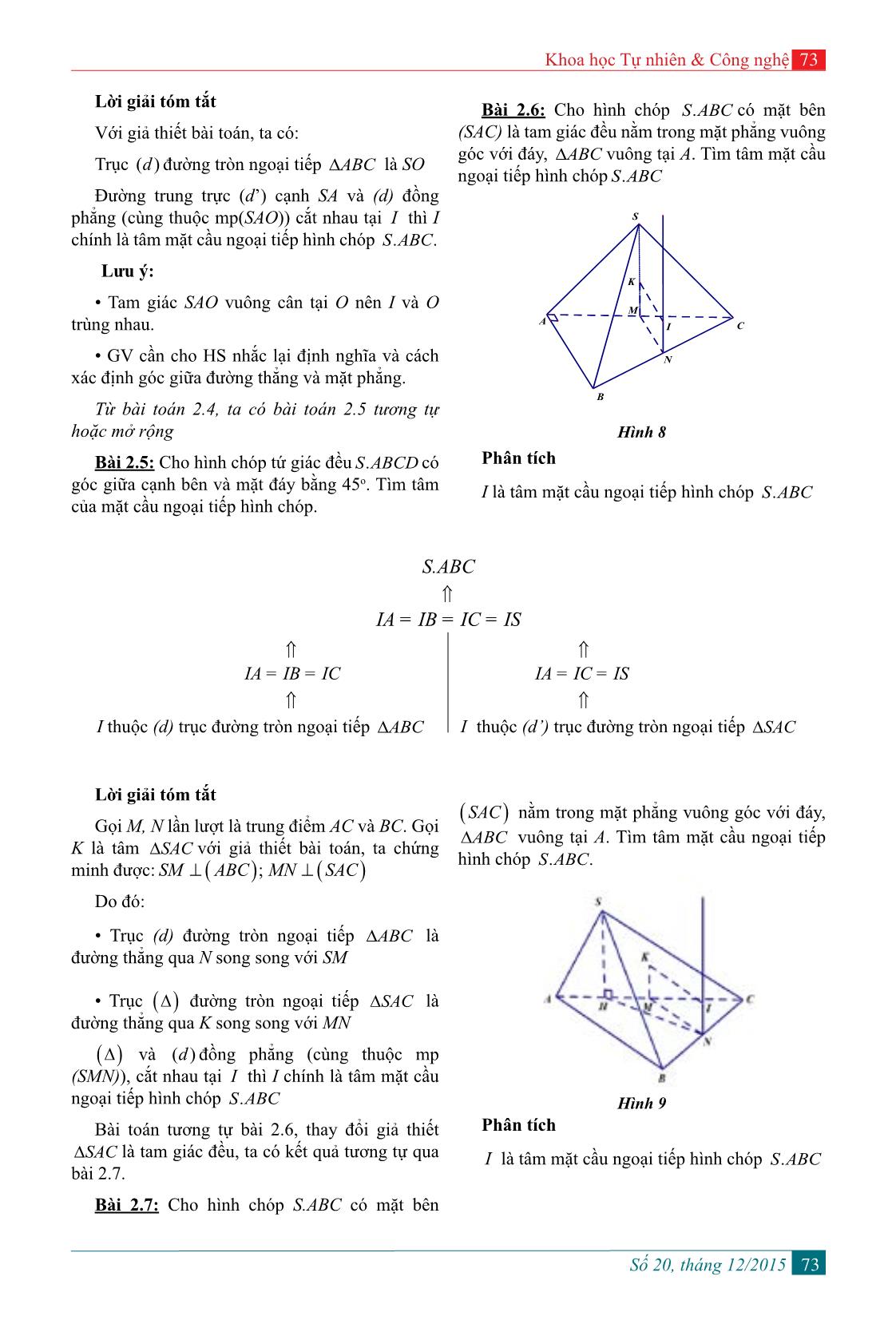
Trang 6

Trang 7

Trang 8
Bạn đang xem tài liệu "Một giải pháp dạy học tiết bài tập hỗ trợ học sinh yếu môn Toán (Chủ đề tìm tâm mặt cầu ngoại tiếp hình chóp)", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Một giải pháp dạy học tiết bài tập hỗ trợ học sinh yếu môn Toán (Chủ đề tìm tâm mặt cầu ngoại tiếp hình chóp)

68 68 Khoa học Tự nhiên & Công nghệ Số 20, tháng 12/2015 MỘT GIẢI PHÁP DẠY HỌC TIẾT BÀI TẬP HỖ TRỢ HỌC SINH YẾU MÔN TOÁN (CHỦ ĐỀ TÌM TÂM MẶT CẦU NGOẠI TIẾP HÌNH CHÓP) AN EFFECTIVE ACTION FOR MATHEMATICS TEACHING AND LEARNING (THEME ON FIND- ING THE CENTER OF A SPHERE WHICH PASSES THROUGH THE VERTICES OF A PYRAMID) Tóm tắt Trong bài viết này, trước tiên, chúng tôi đề cập một số đặc điểm và nguyên nhân của học sinh (HS) yếu môn toán, sau đó đưa ra một giải pháp hỗ trợ HS thông qua bài toán gốc, từ bài toán gốc này đề xuất bài toán tương tự hoặc mở rộng bài toán giúp HS trong việc tìm tâm của mặt cầu ngoại tiếp hình chóp. Từ khóa: học sinh yếu toán, tìm tâm mặt cầu ngoại tiếp hình chóp, bài toán gốc. Abstract This article is first to present the characteristics and causes of students who have poor mathematics performance in order to propose a solution to the improvement of their learning in mathematics through the original (basic) exercise. This exercise is the basis for a similar or more advanced exercise. This will enable to improve their mathematical thought/ skills in finding the center of a sphere which passes through the vertices of a pyramid. Keywords: Students have poor mathematics performance, to find the center of a sphere which passes through vertices of a pyramid, original (basic) exercise. 1. Mở đầu1 Trong quá trình dạy học Toán ở bậc Trung học Phổ thông, chúng tôi nhận thấy học sinh (HS) rất sợ môn Hình học, đặc biệt là hình học không gian. Học sinh yếu Toán chưa biết vận dụng lý thuyết vào giải bài toán có thể kể đến nhiều nguyên nhân như chưa hiểu lý thuyết, không biết vận dụng lý thuyết, không biết bắt đầu giải bài toán từ đâu,... Một số HS có tư tưởng nóng vội, không nắm vững lý thuyết, xem thường các bài toán cơ bản vốn có thể xem là bài toán gốc giúp HS giải các bài toán khó hơn. Với đối tượng là HS yếu môn Toán, việc rèn luyện cho HS phát hiện được dạng bài toán tức là tăng cường hình thức tái hiện tường minh rất quan trọng. Điều đó có nghĩa là HS biết quy bài toán đã cho về các bài toán đã biết cách giải. Trong bài viết này, chúng tôi đề cập một số bài toán liên quan đến chủ đề tìm tâm của mặt cầu ngoại tiếp hình chóp với mục đích: minh họa một số dạng toán cơ bản thể hiện việc vận dụng định nghĩa và phương pháp tìm tâm mặt cầu ngoại tiếp hình chóp nhằm giúp HS nắm vững phương pháp giải toán và vận dụng vào các bài toán tương tự hoặc khó hơn. 2. Nội dung 2.1. Đặc điểm và nguyên nhân của học sinh yếu môn Toán Theo Nguyễn Bá Kim, “sự yếu kém môn Toán 1 Tiến sĩ, Trường Đại học Sài Gòn ở HS có nhiều biểu hiện, thường có ba đặc điểm cơ bản: • Nhiều “lỗ hổng” về tri thức, kỹ năng; • Tiếp thu chậm; • Phương pháp học tập toán chưa tốt”. (Nguyễn Bá Kim 2007, tr.273) Ngoài ra, khả năng tư duy về toán ở một số HS còn hạn chế, HS không có đủ thời gian để suy nghĩ tìm hướng giải quyết cho bài toán. Giáo viên (GV) đôi khi còn chưa quan tâm đến HS, phương pháp dạy học chưa phù hợp với HS chẳng hạn: khai thác bài toán quá sâu, quá khó, giao bài tập về nhà quá nhiều, còn nôn nóng dạy quá nhiều kiến thức,; điều này đôi khi ảnh hưởng đến HS yếu môn Toán. 2.2. Phương hướng hỗ trợ học sinh yếu kém môn Toán Có thể giúp HS yếu kém môn Toán bằng những cách sau đây: a) Đảm bảo trình độ xuất phát GV giúp HS nắm vững các bài toán cơ bản, tăng cường hình thức tái hiện tường minh, tập cho HS phân tích bài toán để tìm hướng giải bài toán và tư duy tại sao giải bài toán như thế. b) Hướng dẫn HS biết cách lấp “lỗ hổng” về kiến thức, kỹ năng Hoa Ánh Tường1 69 69 Khoa học Tự nhiên & Công nghệ Số 20, tháng 12/2015 GV tập cho HS ý thức tự phát hiện và lấp đầy những “lỗ hổng” kiến thức của bản thân bằng cách: tự hệ thống kiến thức liên quan cho từng tiết học, tự tra cứu sách vở, tài liệu để tìm các thông tin có liên quan đến kiến thức,... c) Luyện tập vừa sức HS yếu kém GV gia tăng phù hợp số lượng bài tập cùng thể loại và cùng mức độ. 2.3. Nội dung minh họa Trong phần trình bày này, chúng tôi minh họa bài toán gốc liên quan đến chủ đề tìm tâm của mặt cầu ngoại tiếp hình chóp. Bên cạnh đó, chúng tôi nêu lên cách vận dụng từ bài toán gốc, có những bình luận dưới góc độ thực hành giải toán nhằm giúp người đọc thấy rõ hơn hiệu quả của bài toán gốc được sử dụng qua các bài toán tương tự hoặc mở rộng. Trường hợp 1. Các điểm cùng nhìn một cạnh dưới góc 900 Xét bài toán 1: Cho A, B cố định. Tập hợp các điểm M di động trong không gian sao cho góc AMB bằng 900 là mặt cầu đường kính AB. Nói cách khác: cho hai điểm A, B cố định, điểm M di động sao cho tam giác ABM vuông tại M thì M thuộc mặt cầu đường kính AB. Vận dụng: Nếu các tam giác ABM, ABN, ABC là các tam giác vuông có chung cạnh huyền AB thì A, B, M, N, C cùng thuộc mặt cầu đường kính AB (tâm I của mặt cầu là trung điểm cạnh huyền AB). Nếu M, N, C cùng nhìn cạnh AB dưới góc 900
File đính kèm:
 mot_giai_phap_day_hoc_tiet_bai_tap_ho_tro_hoc_sinh_yeu_mon_t.pdf
mot_giai_phap_day_hoc_tiet_bai_tap_ho_tro_hoc_sinh_yeu_mon_t.pdf

