Mô phỏng cộng hưởng Plasmon bề mặt trên cấu hình Kretschmann bằng phương pháp phần tử hữu hạn

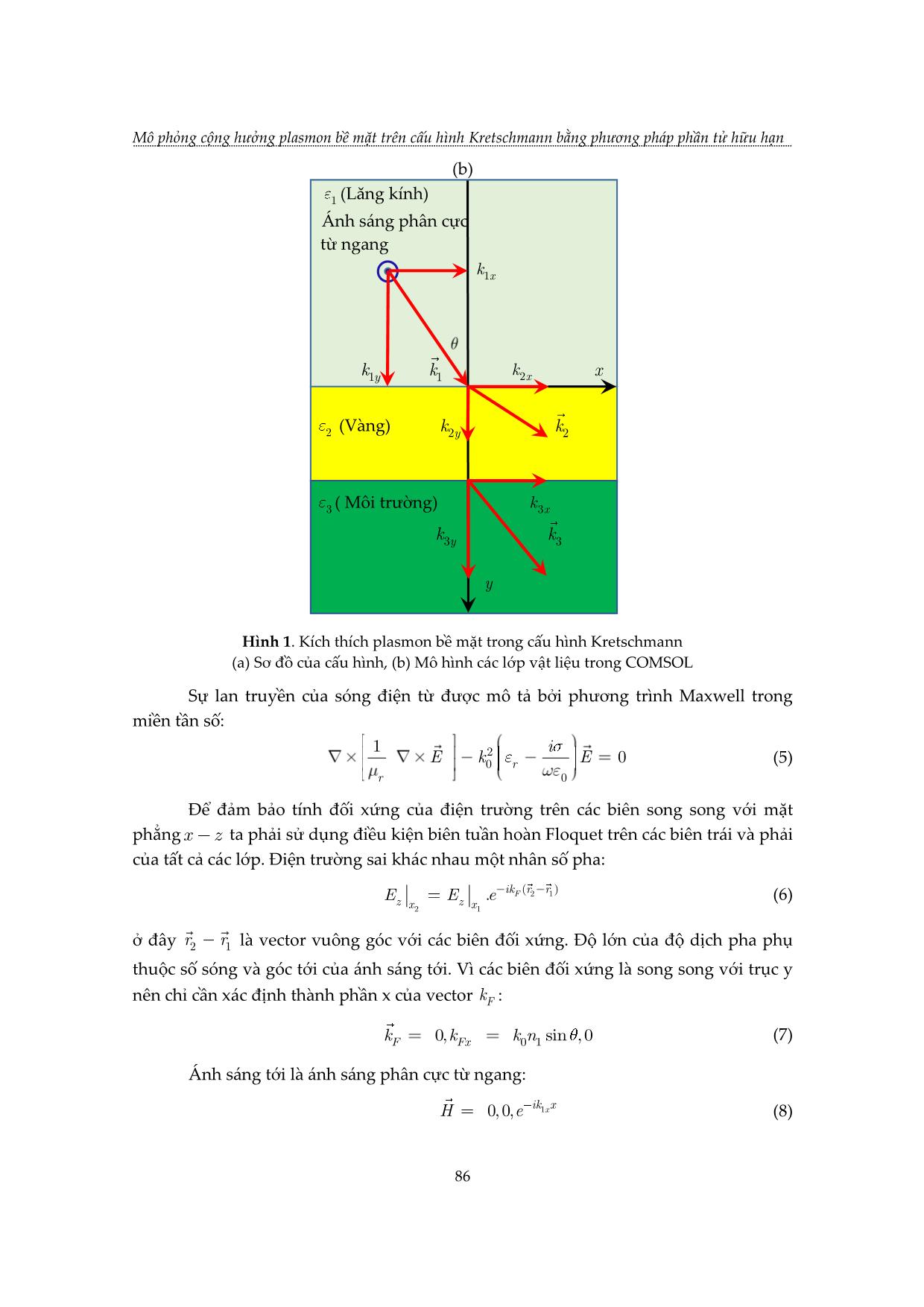
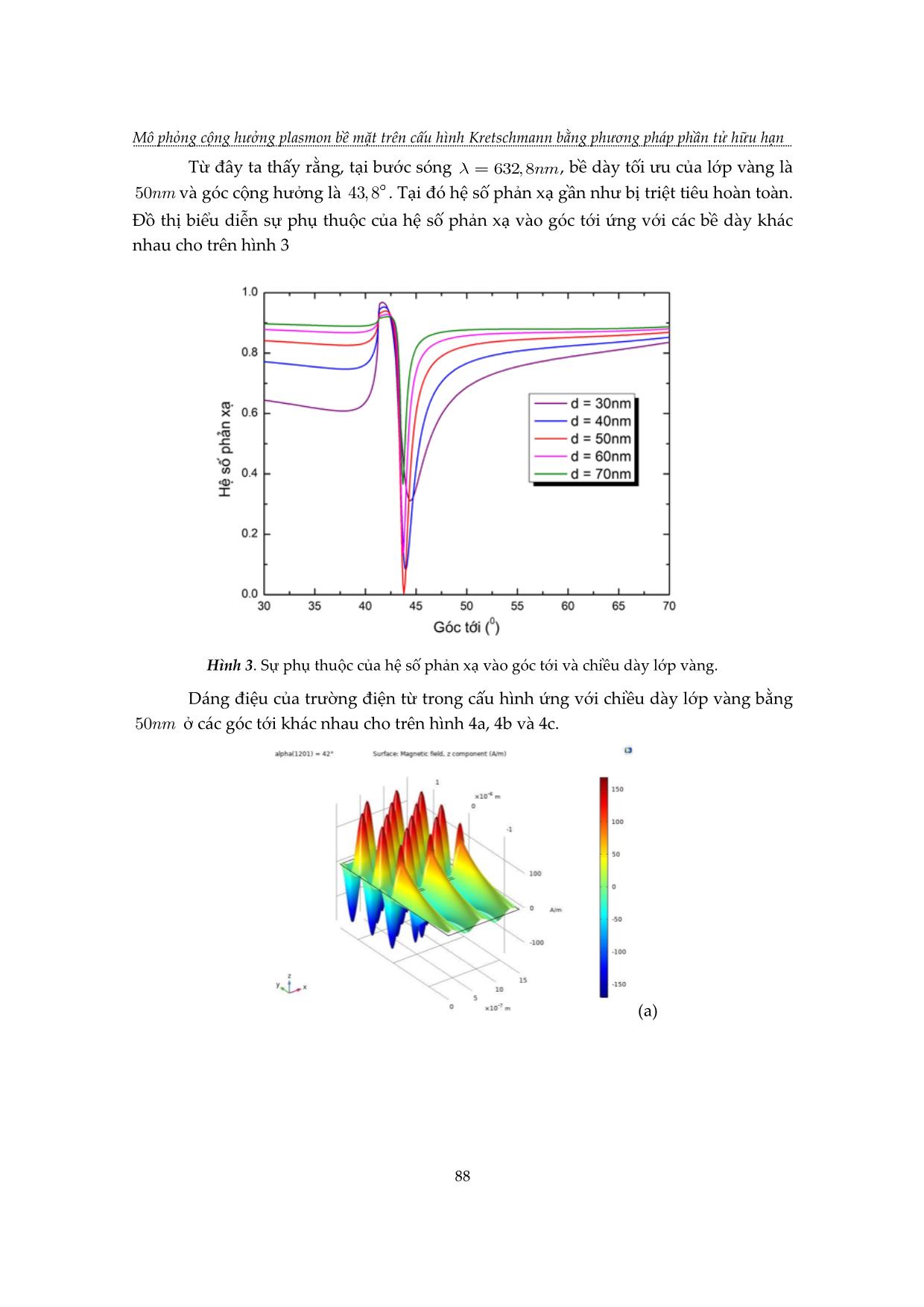
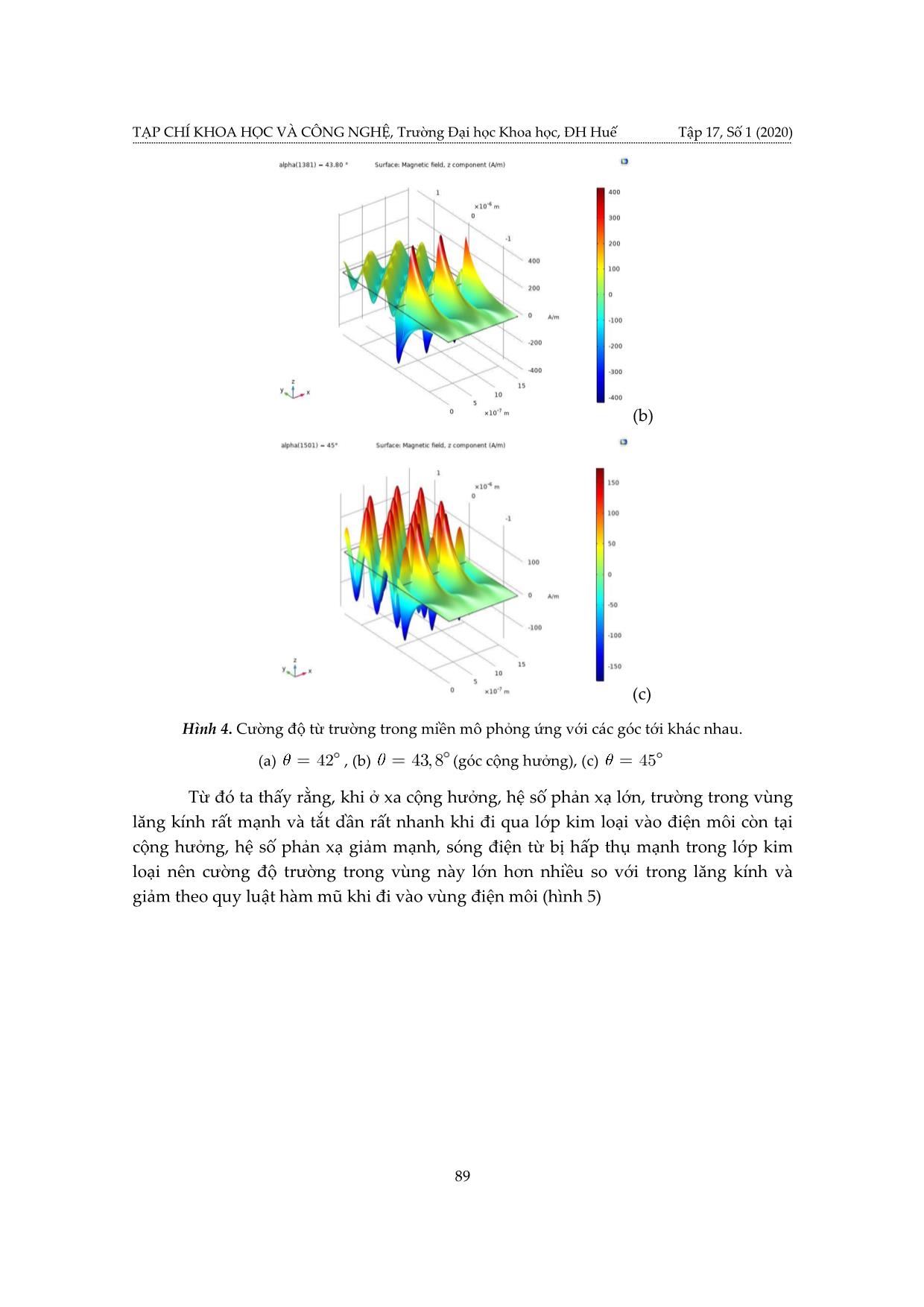
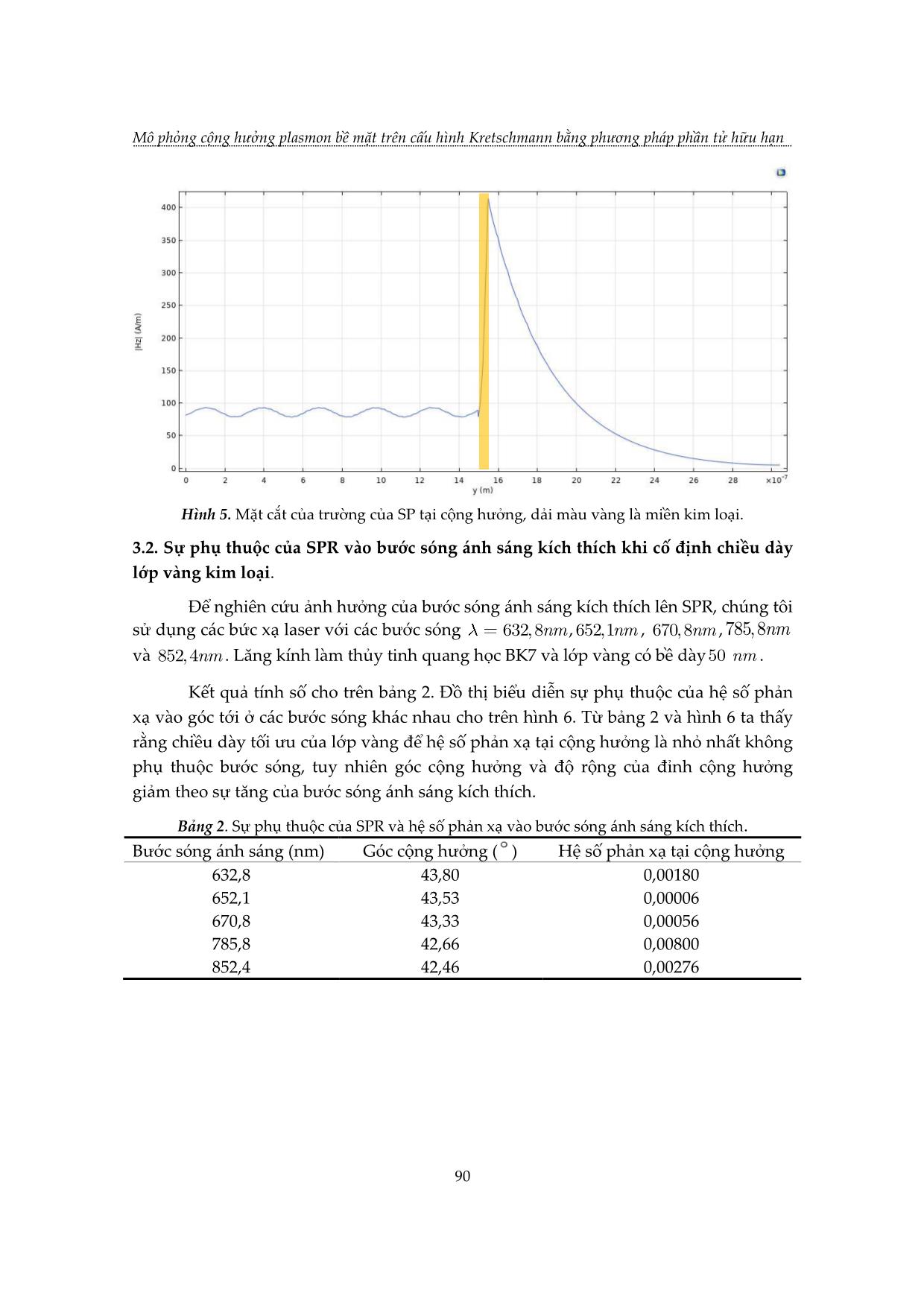
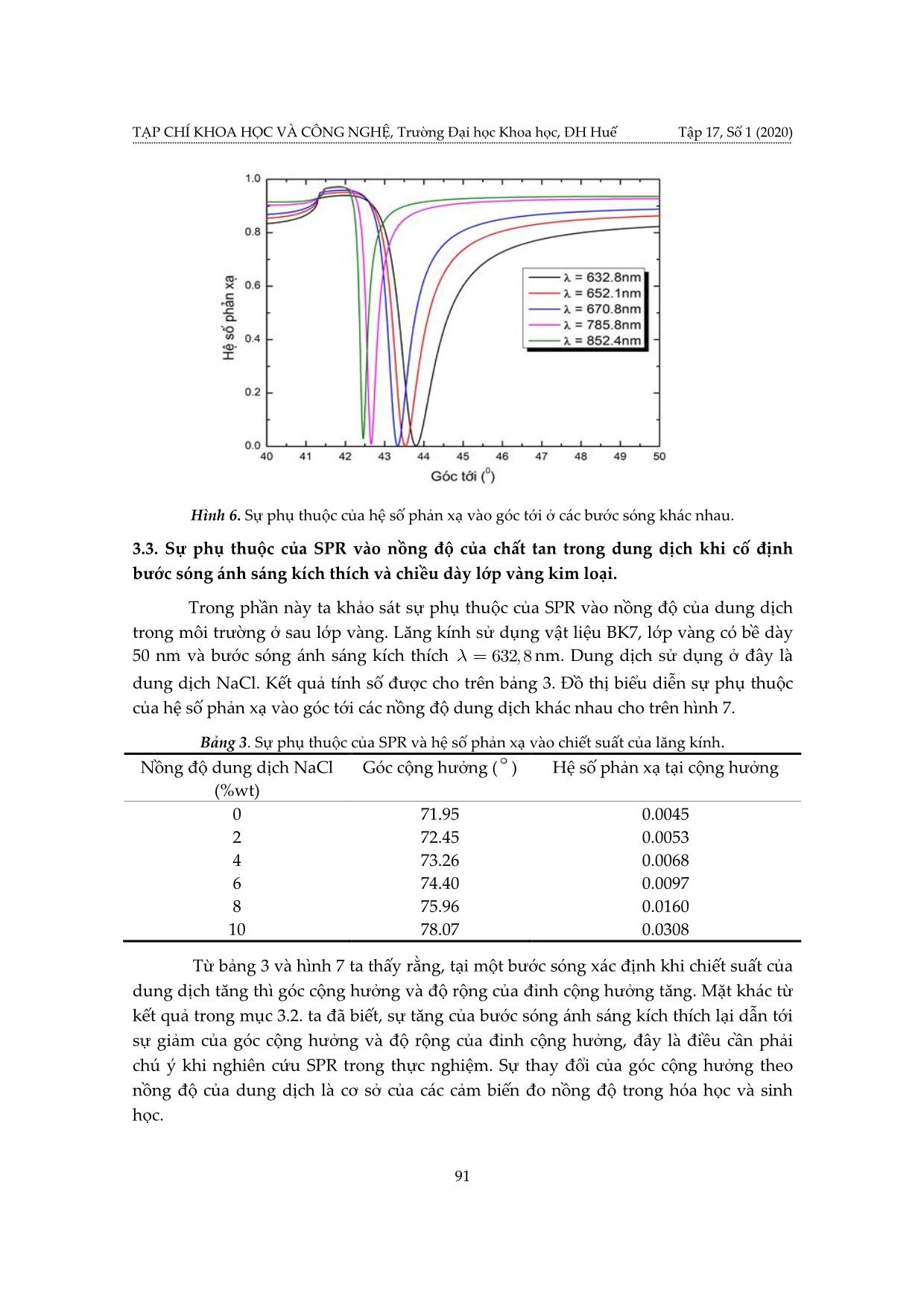
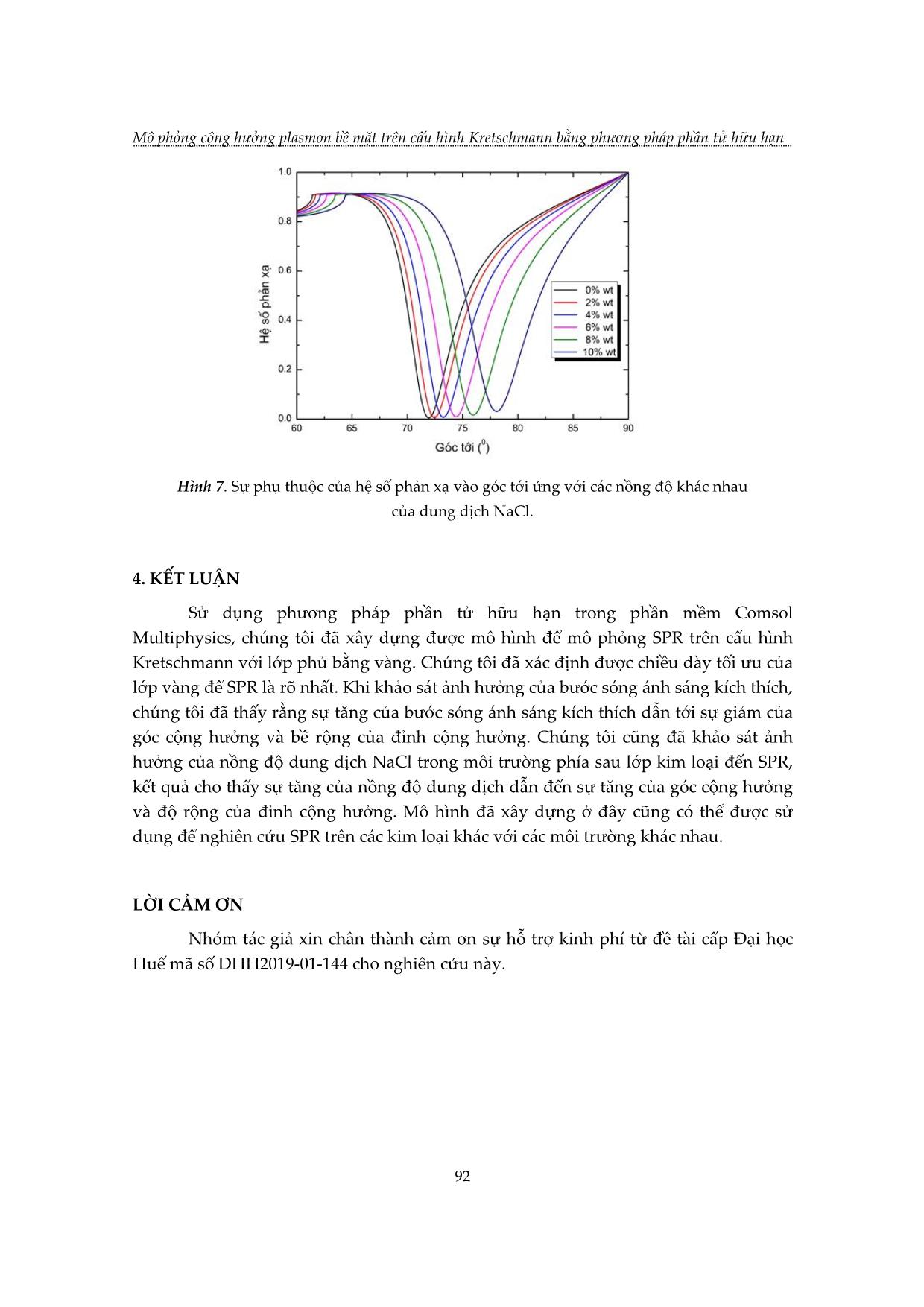
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
 MÔ PHỎNG CỘNG HƯỞNG PLASMON BỀ MẶT TRÊN CẤU HÌNH 
 KRETSCHMANN BẰNG PHƯƠNG PHÁP PHẦN TỬ HỮU HẠN 
 Nguyễn Thị Thùy Dương1, Lê Ngọc Minh2, Lê Phước Định2, 
 Lê Thị Ngọc Bảo2, Võ Thanh Tùng3* 
 1 Trường THPT Nguyễn Trãi, Phú Yên 
 2 Khoa Điện, Điện tử và CNVL, Trường Đại học Khoa học, Đại học Huế 
 3 Trường Đại học Khoa học, Đại học Huế 
 *Email: vttung@hueuni.edu.vn 
 Ngày nhận bài: 15/9/2020; ngày hoàn thành phản biện: 23/9/2020; ngày duyệt đăng: 02/10/2020 
 TÓM TẮT 
 Trong bài báo này, chúng tôi sử dụng phần mềm mô phỏng dựa trên phương 
 pháp phần tử hữu hạn (FEM) để nghiên cứu cộng hưởng plasmon bề mặt (SPR) 
 trên cấu hình Kretschmann với lăng kính được phủ vàng kim loại. Đã xác định 
 được rằng, tại bước sóng 632,8 nm bề dày tối ưu của lớp vàng là 50 nm và hệ số 
 phản xạ đạt cực tiểu tại góc tới 43,80 . Kết quả mô phỏng cũng cho thấy sự giảm 
 của góc cộng hưởng khi tăng bước sóng của ánh sáng kích thích và sự tăng của 
 góc cộng hưởng khi nồng độ của dung dịch tăng. 
 Từ khóa: Cấu hình Kretschmann, SPR, FEM. 
1. MỞ ĐẦU 
 Cộng hưởng plasmon bề mặt (SPR) là một kỹ thuật đầy hứa hẹn trong vài thập 
kỷ gần đầy. Nó có nhiều ứng dụng trong vật lý, hóa học, sinh học [1,2] và an toàn thực 
phẩm [3,4]. Việc quan sát SPR lần đầu tiên được thực hiện bởi Wood [5] vào năm 1902 
trên cách tử nhiễu xạ. Khi một ánh sáng phân cực chiếu vào gương có cách tử, người ta 
quan sát được một vân tối và vân sáng. Điều này thường được gọi là tính dị thường 
Wood. 
 Năm 1941, Fano kết luận rằng những dị thường mà Wood quan sát được là do 
sự kích thích của sóng bề mặt trên bề mặt của cách tử. Ritchie [6], vào năm 1957, đã 
chứng minh về mặt lý thuyết sự kích thích của các plasmon bề mặt (SP) trên bề mặt 
kim loại. Năm 1958, Turbadar [7] , trong khi chiếu sáng các màng kim loại mỏng trên 
một đế, đã quan sát thấy hệ số phản xạ giảm mạnh. 
 83 
Mô phỏng cộng hưởng plasmon bề mặt trên cấu hình Kretschmann bằng phương pháp phần tử hữu hạn 
 Tuy nhiên, hiệu ứng này không được liên kết với SP. Sau đó Otto [8] vào năm 
1968 đã chỉ ra rằng sự sụt giảm này là do kích thích SP làm hệ số phản xạ toàn phần 
bên trong suy giảm. 
 Năm 1971, Kretschmann [9] đã sửa đổi cấu hình của Otto bằng cách đặt lớp kim 
loại bên dưới lăng kính. Trong những năm 1970, SPR được sử dụng để nghiên cứu các 
đặc tính màng mỏng [10,11] và như một đầu dò cho bề mặt điện hóa [12]. Sau đó, hiện 
tượng SPR dẫn đến sự phát triển của các cảm biến, đặc biệt là nhằm mục đích phát 
hiện khí và cảm biến sinh học[13-15]. Từ đường cong SPR, phản ánh mối quan hệ giữa 
góc tới của ánh sáng và hệ số phản xạ tại cộng hưởng, người ta có thể thu thập được 
các thông tin sinh học và hóa học của môi trường. 
 Với sự phát triển của các phần mềm máy tính, bằng cách mô phỏng hiện tượng 
SPR, dữ liệu lý thuyết có thể được thu thập để đưa ra lựa chọn tối ưu cho thử nghiệm 
SPR. Trong bài báo này chúng tôi sử dụng phần mềm COMSOL Multiphysics [13] để 
mô phỏng SPR trên cấu hình Kretschmann với kim loại vàng bằng cách giải phương 
trình Maxwell trong miền tần số bằng phương pháp phần tử hữu hạn. Trong phần 2 
chúng tôi sẽ giới thiệu các khái niệm cơ sở của SPR, các phương trình mô tả và hình 
học của mô hình khảo sát SPR. Trong phần 3 trình bày các kết quả nhận được khi thực 
hiện mô phỏng: bề dày tối ưu của lớp vàng tại đó hệ số phản xạ đạt cực tiểu và góc 
cộng hưởng tương ứng, sự thay đổi của góc cộng hưởng theo bước sóng của ánh sáng 
tới và nồng độ của dung dịch NaCl. 
2. CƠ SỞ LÝ THUYẾT VÀ MÔ HÌNH 
 Khi áp đặt điện trường lên bề mặt của kim loại sẽ gây nên chuyển động của các 
electron tự do. Các electron tự do này lại chịu lực hút tác động theo chiều ngược lại của 
các ion dương trong mạng nền. Dao động tập thể này của các electron được gọi là các 
plassmon. Cộng hưởng plasmon bề mặt (SPR) là sự kích thích plasmon tại mặt phân 
cách của kim loại và điện môi bằng ánh sáng tới. Điều kiện cộng hưởng được thỏa mãn 
khi tần số của ánh sáng phù hợp với tần số riêng của dao động các electron trên bề 
mặt. Để mô tả một cách đơn giản sự tồn tại và tính chất của plasmon bề mặt, ta coi mỗi 
lớp vật liệu là một môi trường liên tục đồng nhất, trong đó hằng số điện môi của vật 
liệu có giá trị phức. Để tồn tại plasmon bề mặt, phần thực của hằng số điện môi của 
kim loại phải âm và giá trị tuyệt đối của nó phải lớn hơn hằng số điện môi của môi 
trường. Trên hình 1 là sơ đồ của cấu hình Kretschmann để kích thích plasmon và mô 
hình các lớp vật liệu trên COMSOL. 
 Trong cấu trúc này, một lớp kim loại bằng vàng nằm giữa hai lớp là lăng kính 
và môi trường (nước, không khí hoặc các loại dung dịch cần khảo sát). Ánh sáng tới là 
ánh sáng phân cực từ ngang. Gọi k1,, k 2 k 3 lần lượt là vector sóng của ánh sáng tới, ánh 
 84 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
sáng khúc xạ trong lớp vàng và môi trường, khi đó các thành phần kk11xy, của vector 
sóng của ánh sáng tới bằng: 
 kknkkn101101xysin,cos (1) 
trong đó n11là chiết suất của môi trường tới, k002 là số sóng và 0 là bước 
sóng áng sáng trong chân không. Do tính liên tục của thành phần tiếp tuyến của điện 
trường dọc theo mặt phân cách, các thành phần ngang của các vector sóng được bảo 
toàn khi đi qua các môi trường: 
 kkkkn12301xxx sin (2) 
Các thành phần k2y và k3y được xác định bởi các hệ thức sau: 
 22222222
 kkkkkkkk2022230333 xyxy , (3) 
Do đó: 
 2222
 kkkkkk20213031yxyx ,, (4) 
 (a) 
 85 
Mô phỏng cộng hưởng plasmon bề mặt trên cấu hình Kretschmann bằng phương pháp phần tử hữu hạn 
 (b) 
 1 (Lăng kính) 
 Ánh sáng phân cực 
 từ ngang 
 k1x 
 k1y k1 k2x x 
 2 (Vàng) k2y k2 
 3 ( Môi trường) k3x 
 k3y k3 
 y 
 Hình 1. Kích thích plasmon bề mặt trong cấu hình Kretschmann 
 (a) Sơ đồ của cấu hình, (b) Mô hình các lớp vật liệu trong COMSOL 
 Sự lan truyền của sóng điện từ được mô tả bởi phương trình Maxwell trong 
miền tần số: 
 1 2 i
 EkE 0 r 0 (5) 
 r 0
 Để đảm bảo tính đối xứng của điện trường trên các biên song song với mặt 
phẳngxz ta phải sử dụng điều kiện biên tuần hoàn Floquet trên các biên trái và phải 
của tất cả các lớp. Điện trường sai khác nhau một nhân số pha: 
 ikrrF ()21
 EEezz. (6) 
 xx21
ở đây rr21 là vector vuông góc với các biên đối xứng. Độ lớn của độ dịch pha phụ 
thuộc số sóng và góc tới của ánh sáng tới. Vì các biên đối xứng là song song với trục y 
nên chỉ cần xác định thành phần x của vector kF : 
 kF0, k Fx k01 n sin ,0 (7) 
 Ánh sáng tới là ánh sáng phân cực từ ngang: 
 ik x
 He0,0, 1x (8) 
 86 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
3. KẾT QUẢ VÀ THẢO LUẬN 
 Việc mô phỏng SPR trên cấu hình Kretschmann bằng phương pháp phần tử 
hữu hạn được thực hiện bằng việc giải số phương trình (5) với các điều kiện (6) - (8) 
trên phần mềm COMSOL Multiphysics. Trên hình 2 là hình học của miền tính toán sau 
khi được chia lưới. Kích thước của miền lăng kính là 1,5 1,5mm, lớp vàng có bề 
dày d và bề rộng 1,5 m và kích thước của môi trường là 1,5 1,5mm. Để đảm bảo 
cho tính vô hạn theo trục x , điều kiện biên tuần hoàn Floquet được áp đặt trên hai 
biên ở hai bên của miền tính toán, khi sóng tới biên bên phải sẽ chuyển qua biên bên 
trái với độ dịch pha tương ứng và điều này không ảnh hưởng đến kết quả tính toán. 
 Hình 2. Mô hình tính toán được chia lưới và áp đặt điều kiện biên tuần hoàn. 
3.1. Sự phụ thuộc của SPR vào bề dày của lớp kim loại. 
 Để nghiên cứu ảnh hưởng của bề dày lớp kim loại lên SPR, chúng tôi sử dụng 
ánh sáng tới là bức xạ laser He – Ne với bước sóng 632.8nm , lăng kính làm bằng 
thủy tinh quang học BK7 có chiết suất n 1,5151[17]; kim loại là vàng có hằng số điện 
môi 11,7401,2611 i [17] và môi trường là không khí. Chiều dày của lớp vàng 
thay đổi từ 20nm đến 70nm. Góc tới thay đổi trong khoảng 3060 . Kết quả tính số 
cho trên bảng 1. 
 Bảng 1. Sự phụ thuộc của SPR và hệ số phản xạ vào chiều dày lớp vàng. 
Chiều dày lớp vàng (nm) Góc cộng hưởng ( ) Hệ số phản xạ tại cộng hưởng 
 30 44,44 0,3108 
 35 44,15 0,1849 
 40 43,98 0,0807 
 45 43,87 0,0154 
 50 43,80 0,0018 
 55 43,75 0,0427 
 60 43,73 0,1289 
 65 43,71 0,2427 
 70 43,70 0,3653 
 87 
Mô phỏng cộng hưởng plasmon bề mặt trên cấu hình Kretschmann bằng phương pháp phần tử hữu hạn 
 Từ đây ta thấy rằng, tại bước sóng 6 3 2,8nm , bề dày tối ưu của lớp vàng là 
50nm và góc cộng hưởng là 4 3, 8 . Tại đó hệ số phản xạ gần như bị triệt tiêu hoàn toàn. 
Đồ thị biểu diễn sự phụ thuộc của hệ số phản xạ vào góc tới ứng với các bề dày khác 
nhau cho trên hình 3 
 Hình 3. Sự phụ thuộc của hệ số phản xạ vào góc tới và chiều dày lớp vàng. 
 Dáng điệu của trường điện từ trong cấu hình ứng với chiều dày lớp vàng bằng 
50nm ở các góc tới khác nhau cho trên hình 4a, 4b và 4c. 
 (a) 
 88 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
 (b) 
 (c) 
 Hình 4. Cường độ từ trường trong miền mô phỏng ứng với các góc tới khác nhau. 
 (a) 42 , (b) 43,8 (góc cộng hưởng), (c) 45 
 Từ đó ta thấy rằng, khi ở xa cộng hưởng, hệ số phản xạ lớn, trường trong vùng 
lăng kính rất mạnh và tắt dần rất nhanh khi đi qua lớp kim loại vào điện môi còn tại 
cộng hưởng, hệ số phản xạ giảm mạnh, sóng điện từ bị hấp thụ mạnh trong lớp kim 
loại nên cường độ trường trong vùng này lớn hơn nhiều so với trong lăng kính và 
giảm theo quy luật hàm mũ khi đi vào vùng điện môi (hình 5) 
 89 
Mô phỏng cộng hưởng plasmon bề mặt trên cấu hình Kretschmann bằng phương pháp phần tử hữu hạn 
 Hình 5. Mặt cắt của trường của SP tại cộng hưởng, dải màu vàng là miền kim loại. 
3.2. Sự phụ thuộc của SPR vào bước sóng ánh sáng kích thích khi cố định chiều dày 
lớp vàng kim loại. 
 Để nghiên cứu ảnh hưởng của bước sóng ánh sáng kích thích lên SPR, chúng tôi 
sử dụng các bức xạ laser với các bước sóng 632,8nm , 652,1nm , 670,8nm ,785,8nm 
và 852,4nm . Lăng kính làm thủy tinh quang học BK7 và lớp vàng có bề dày50 nm . 
 Kết quả tính số cho trên bảng 2. Đồ thị biểu diễn sự phụ thuộc của hệ số phản 
xạ vào góc tới ở các bước sóng khác nhau cho trên hình 6. Từ bảng 2 và hình 6 ta thấy 
rằng chiều dày tối ưu của lớp vàng để hệ số phản xạ tại cộng hưởng là nhỏ nhất không 
phụ thuộc bước sóng, tuy nhiên góc cộng hưởng và độ rộng của đỉnh cộng hưởng 
giảm theo sự tăng của bước sóng ánh sáng kích thích. 
 Bảng 2. Sự phụ thuộc của SPR và hệ số phản xạ vào bước sóng ánh sáng kích thích. 
Bước sóng ánh sáng (nm) Góc cộng hưởng ( ) Hệ số phản xạ tại cộng hưởng 
 632,8 43,80 0,00180 
 652,1 43,53 0,00006 
 670,8 43,33 0,00056 
 785,8 42,66 0,00800 
 852,4 42,46 0,00276 
 90 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
 Hình 6. Sự phụ thuộc của hệ số phản xạ vào góc tới ở các bước sóng khác nhau. 
3.3. Sự phụ thuộc của SPR vào nồng độ của chất tan trong dung dịch khi cố định 
bước sóng ánh sáng kích thích và chiều dày lớp vàng kim loại. 
 Trong phần này ta khảo sát sự phụ thuộc của SPR vào nồng độ của dung dịch 
trong môi trường ở sau lớp vàng. Lăng kính sử dụng vật liệu BK7, lớp vàng có bề dày 
50 nm và bước sóng ánh sáng kích thích 632,8 nm. Dung dịch sử dụng ở đây là 
dung dịch NaCl. Kết quả tính số được cho trên bảng 3. Đồ thị biểu diễn sự phụ thuộc 
của hệ số phản xạ vào góc tới các nồng độ dung dịch khác nhau cho trên hình 7. 
 Bảng 3. Sự phụ thuộc của SPR và hệ số phản xạ vào chiết suất của lăng kính. 
 Nồng độ dung dịch NaCl Góc cộng hưởng ( ) Hệ số phản xạ tại cộng hưởng 
 (%wt) 
 0 71.95 0.0045 
 2 72.45 0.0053 
 4 73.26 0.0068 
 6 74.40 0.0097 
 8 75.96 0.0160 
 10 78.07 0.0308 
 Từ bảng 3 và hình 7 ta thấy rằng, tại một bước sóng xác định khi chiết suất của 
dung dịch tăng thì góc cộng hưởng và độ rộng của đỉnh cộng hưởng tăng. Mặt khác từ 
kết quả trong mục 3.2. ta đã biết, sự tăng của bước sóng ánh sáng kích thích lại dẫn tới 
sự giảm của góc cộng hưởng và độ rộng của đỉnh cộng hưởng, đây là điều cần phải 
chú ý khi nghiên cứu SPR trong thực nghiệm. Sự thay đổi của góc cộng hưởng theo 
nồng độ của dung dịch là cơ sở của các cảm biến đo nồng độ trong hóa học và sinh 
học. 
 91 
Mô phỏng cộng hưởng plasmon bề mặt trên cấu hình Kretschmann bằng phương pháp phần tử hữu hạn 
 Hình 7. Sự phụ thuộc của hệ số phản xạ vào góc tới ứng với các nồng độ khác nhau 
 của dung dịch NaCl. 
4. KẾT LUẬN 
 Sử dụng phương pháp phần tử hữu hạn trong phần mềm Comsol 
Multiphysics, chúng tôi đã xây dựng được mô hình để mô phỏng SPR trên cấu hình 
Kretschmann với lớp phủ bằng vàng. Chúng tôi đã xác định được chiều dày tối ưu của 
lớp vàng để SPR là rõ nhất. Khi khảo sát ảnh hưởng của bước sóng ánh sáng kích thích, 
chúng tôi đã thấy rằng sự tăng của bước sóng ánh sáng kích thích dẫn tới sự giảm của 
góc cộng hưởng và bề rộng của đỉnh cộng hưởng. Chúng tôi cũng đã khảo sát ảnh 
hưởng của nồng độ dung dịch NaCl trong môi trường phía sau lớp kim loại đến SPR, 
kết quả cho thấy sự tăng của nồng độ dung dịch dẫn đến sự tăng của góc cộng hưởng 
và độ rộng của đỉnh cộng hưởng. Mô hình đã xây dựng ở đây cũng có thể được sử 
dụng để nghiên cứu SPR trên các kim loại khác với các môi trường khác nhau. 
LỜI CẢM ƠN 
 Nhóm tác giả xin chân thành cảm ơn sự hỗ trợ kinh phí từ đề tài cấp Đại học 
Huế mã số DHH2019-01-144 cho nghiên cứu này. 
 92 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
 TÀI LIỆU THAM KHẢO 
[1]. Liedberg B., Nylander C. and Lunström I. (1983). Surface plasmon resonance for gas 
 detection and biosensing. Sens. Actuators, Vol.4, pp. 299–304. 
[2]. Villuendas F. and Pelayo J. (1990). Optical fibre device for chemical sensing based on 
 surface plasmon excitridon. Sens. Actuators A. Phys., Vol.23, pp.1142–1145. 
[3]. Piliarik M., Parova L. and Homola J. (2009). High-throughput SPR sensor for food safety. 
 Biosens. Bioelectron. Vol.24, pp.1399-1404. 
[4]. Homola J. (2006). Surface plasmon resonance (SPR) biosensors and their applications in 
 food safety and security. Frontiers in Planar Lightwave Circuit Technology, Springer, pp. 101–
 118. 
[5]. Wood R.W. (1902). On a Remarkable Case of Uneven Distribution of Light in a Diffraction 
 Grating Spectrum. Proceedings of the Physical Society of London, Vol.18, Iss.1, pp. 269-275. 
[6]. Ritchie R.H. (1957). Plasma Losses by Fast Electrons in Thin Films. Physical Review. Vol.106, 
 Iss.5, pp. 874-881. 
[7]. Turbadar T. (1959) Complete absorption of light by thin metal films. Proc. Phys. Soc. Vol. 73, 
 pp. 40–44. 
[8]. Otto A. (1968). Excitation of nonradiative surface plasma waves in silver by the method of 
 frustrated total reflection. Zeitschrift Fur Physik. Vol.216, Iss.4, pp. 398-410. 
[9]. Kretschmann E. and Raether H. (1968) Radiative decay of nonradiative surface plasmons 
 excited by light. Z. Naturforsch. A. Vol.23, pp. 2135-2136. 
[10]. Pockrand I. et al., (1978) Surface plasmon spectroscopy of organic monolayer assemblies. 
 Surf. Sci. Vol. 74, pp. 237–244. 
[11]. Pockrand I. et al., (1978) Optical properties of organic dye monolayers by surface plasmon 
 spectroscopy. J. Chem. Phys., Vol. 69, pp. 4001–4011. 
[12]. Gordon J. and Ernst S. (1980) Surface plasmons as a probe of the electrochemical interface. 
 Surf. Sci., Vol. 101, pp. 499–506. 
[13]. Patel K., Halevi S., Melman P., Schwartz J., Cai S. and Singh B. (2017). A Novel Surface 
 Plasmon Resonance Biosensor for the Rapid Detection of Botulinum Neurotoxins. 
 Biosensors, Vol. 7, Iss. 4, 32 
[14]. Firdous S., Anwar S. and Rafya R. (2018). Development of surface plasmon resonance 
 (SPR) biosensors for use in the diagnostics of malignant and infectious diseases. Laser 
 Physics Letters, Vol. 15, Iss. 6, 065602(5pp). 
[15]. Baschir L., Popescu A. A., Savastru D. and Miclos S. (2020). Surface Plasmon Resonance 
 Chemical Sensors Based on Amorphous Chalcogenide Waveguides. Macromolecular 
 Symposia, Vol. 389, Iss. 1, 1900066. 
[16]. COMSOL Multiphysics® Modeling Software. Website: www.comsol.com 
[17]. https://refractiveindex.info/ 
 93 
Mô phỏng cộng hưởng plasmon bề mặt trên cấu hình Kretschmann bằng phương pháp phần tử hữu hạn 
 SIMULATION OF SURFACE PLASMON RESONACE ON KRETSCHMANN 
 CONFIGURATION BY FINITE ELEMENT METHOD 
 Nguyen Thi Thuy Duong1, Le Ngoc Minh2, Le Phuoc Dinh2, 
 Le Thi Ngoc Bao2, Vo Thanh Tung3* 
 1 Nguyen Trai High School, Phu Yen, Vietnam 
 2 Faculty of Electronics, Electrical Engineering and Material Technology, 
 University of Sciences, Hue University 
 3 University of Sciences, Hue University 
 *Email: vttung@hueuni.edu.vn 
 ABSTRACT 
 In this paper, we use a modeling software based on finite element method (FEM) 
 to study surface plasmon resonance (SPR) on Kretschmann configuration with 
 prisms coated with gold metal. It was determined that, at wavelength 632,8 nm, the 
 optimal thickness of the gold layer was 50 nm and the reflectance falling to a 
 minimum at an angle of 43,80. The simulation results also showed a decrease of the 
 resonant angle with increasing wavelength of the excitation light, and increase of 
 the resonant angle with increases of concentration of the solution. 
 Keywords: Kretschmann configuration, SPR, FEM. 
 94 
TẠP CHÍ KHOA HỌC VÀ CÔNG NGHỆ, Trường Đại học Khoa học, ĐH Huế Tập 17, Số 1 (2020) 
 Nguyễn Thùy Dương sinh ngày 12/03/1986 tại Phú Yên. Năm 2009, bà tốt 
 nghiệp cử nhân ngành Sư phạm Vật lý tại Trường Đại học Qui Nhơn. 
 Hiện nay bà là giáo viên Vật lý tại Trường THPT Nguyễn Trãi, Tp Tuy 
 Hòa, tỉnh Phú Yên và đang theo học thạc sĩ chuyên ngành Vật lý Chất rắn 
 tại Trường Đại học Khoa Học, Đại học Huế khóa 2018-2020. 
 Võ Thanh Tùng sinh ngày 17/07/1979 tại Quảng Bình. Năm 2001, ông tốt 
 nghiệp cử nhân ngành Vật lý Chất rắn tại Trường Đại học Tổng hợp Huế. 
 Năm 2004, ông tốt nghiệp thạc sĩ chuyên ngành Vật lý Chất rắn. Năm 
 2009, ông tốt nghiệp tiến sĩ chuyên ngành Vật lý Chất rắn tại Belarus. 
 Năm 2015, ông được phong hàm PGS và hiện nay là Hiệu trưởng Trường 
 Đại học Khoa học, Đại học Huế. 
 Lĩnh vực nghiên cứu: Vật liệu áp điện, kỹ thuật siêu âm, mô phỏng lý 
 thuyết, kỹ thuật vi xử lý và ứng dụng, xử lý tín hiệu số 
 Lê Ngọc Minh sinh ngày 06/12/1963 tại Nam Định. Năm 1985, ông tốt 
 nghiệp cử nhân ngành Vật lý lý thuyết tại trường Đại học Tổng hợp Huế. 
 Năm 1998, ông tốt nghiệp thạc sĩ chuyên ngành Vật lý Chất rắn và hiện 
 nay công tác tại Trường Đại học Khoa học, Đại học Huế. 
 Lĩnh vực nghiên cứu: lý thuyết chất rắn, vật lý tính toán, kỹ thuật siêu âm, 
 mô phỏng  
 Lê Phước Định sinh ngày 15/10/1991 tại Thành phố Huế. Năm 2014, ông 
 tốt nghiệp cử nhân ngành Vật lý Chất rắn tại trường Đại học Khoa học, 
 Đại học Huế. Năm 2017, ông tốt nghiệp Thạc sĩ chuyên ngành Vật lý Chất 
 rắn và hiện nay công tác tại trường Đại học Khoa học, Đại học Huế. 
 Lĩnh vực nghiên cứu: vật lý chất rắn, kỹ thuật siêu âm, mô phỏng 
 Lê Thị Ngọc Bảo sinh ngày 31/10/1983 tại Thừa Thiên Huế. Năm 2006, bà 
 tốt nghiệp Cử nhân ngành Vật lý tại Trường Đại học Khoa học, Đại học 
 Huế. Năm 2009, bà tốt nghiệp Thạc sĩ chuyên ngành Vật lý lý thuyết và 
 Vật lý toán tại trường Đại học Sư phạm, Đại học Huế. Năm 2020 bà tốt 
 nghiệp tiến sĩ chuyên ngành Vật lý lý thuyết và vật lý toán tại trường Đại 
 học Sư phạm, Đại học Huế. Từ năm 2006 đến nay bà công tác tại trường 
 Đại học Khoa học, Đại học Huế. 
 Lĩnh vực nghiên cứu: Vật lý hệ thấp chiều, vật lý mô phỏng. 
 95 
Mô phỏng cộng hưởng plasmon bề mặt trên cấu hình Kretschmann bằng phương pháp phần tử hữu hạn 
 96