Magnetization in high-tc superconductors
A interesting feature of magnetization curves intersecting atthe same point for a wide
range of magnetic fieldswas observed in high-Tcsuperconductors long time ago, such as
Bi2Sr2CaCu2O8+(BSCCO) [1], YBa2Cu3O7- (YBCO) [2]. It was found that theintersection
point was no longer the same for all the magneticfields in several classes of layered highTcsuperconductors, such asHgBa2Ca2Cu3O8+(HBCCO) [3], La2-xSrxCuO4(LaSCO) [4].
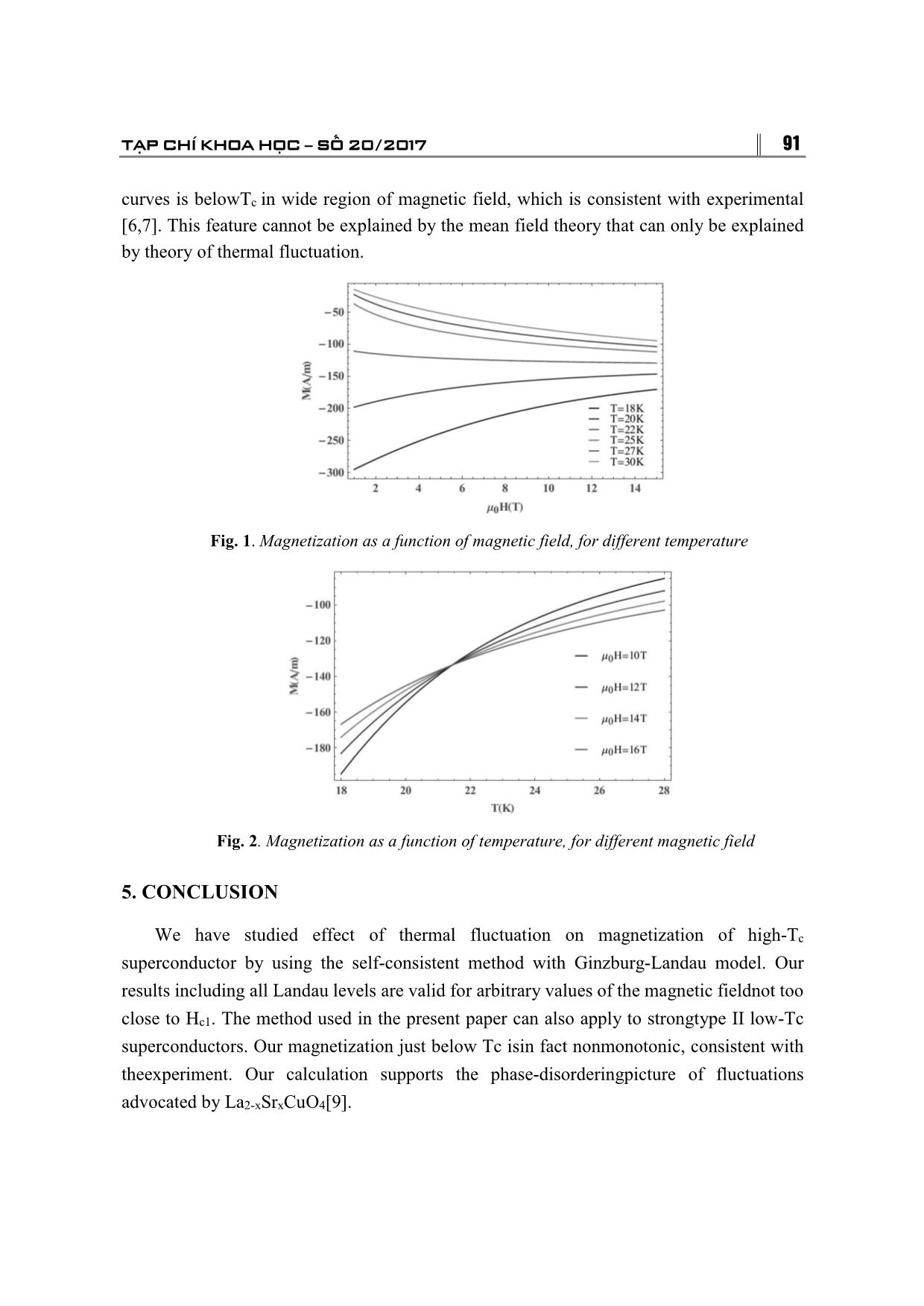
Normally, for superconductormaterials such as YBCO, HBCCO, and optimally doped
LaSCO,the intersection point moves from a high temperature at lowfields to a lower
temperature as the magnetic field increases.The intersection point is always belowTc.
Magnetization in high-Tc superconductorshas been studied theoretically [5] within both
the microscopic theory and the Ginzburg-Landau approach. In all of these calculations the
fluctuationswere assumed to be small enough, so they can be taken intoaccount
perturbatively. To determine theoreticallyfluctuation magnetization for strong thermal
fluctuations,we therefore must go beyond this simple approximationneglecting the effect of
the quartic term in the Ginzburg-Landau freeenergy. The effect of the quartic term in
Ginzburg-Landau free energy is taken into accountwithin the self-consistent theory.

Trang 1

Trang 2

Trang 3

Trang 4
Trang 5

Trang 6
Tóm tắt nội dung tài liệu: Magnetization in high-tc superconductors

TẠP CHÍ KHOA HỌC SỐ 20/2017 87 MAGNETIZATION IN HIGH-TC SUPERCONDUCTORS Bui Duc Tinh, Le Minh Thu, Nguyen Quang Hoc Hanoi National University of Education Abstract: We use the self-consistent method in the presence of magnetic field for the Ginzburg-Landau description of strongly thermal fluctuations effects to calculate magnetization in high-Tc superconductors. The obtained results are summation over all Landau levels which are valid for arbitrary values of the magnetic field not too close to Hc1. It is showed that the intersection point of magnetization curves appears and magnetization just below Tc is nonmonotonic. Our calculation supports the phase disordering picture of fluctuations above Tc. Keywords: Magnetization, superconductor, magnetic, high-Tc Email: bdtinh@hnue.edu.vn Received 05 December 2017 Accepted for publication 25 December 2017 1. INTRODUCTION A interesting feature of magnetization curves intersecting atthe same point for a wide range of magnetic fieldswas observed in high-Tcsuperconductors long time ago, such as Bi2Sr2CaCu2O8+(BSCCO) [1], YBa2Cu3O7- (YBCO) [2]. It was found that theintersection point was no longer the same for all the magneticfields in several classes of layered high- Tcsuperconductors, such asHgBa2Ca2Cu3O8+(HBCCO) [3], La2-xSrxCuO4(LaSCO) [4]. Normally, for superconductormaterials such as YBCO, HBCCO, and optimally doped LaSCO,the intersection point moves from a high temperature at lowfields to a lower temperature as the magnetic field increases.The intersection point is always belowTc. Magnetization in high-Tc superconductorshas been studied theoretically [5] within both the microscopic theory and the Ginzburg-Landau approach. In all of these calculations the fluctuationswere assumed to be small enough, so they can be taken intoaccount perturbatively. To determine theoreticallyfluctuation magnetization for strong thermal fluctuations,we therefore must go beyond this simple approximationneglecting the effect of the quartic term in the Ginzburg-Landau freeenergy. The effect of the quartic term in Ginzburg-Landau free energy is taken into accountwithin the self-consistent theory. 88 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 2. GINZBURG-LANDAU MODEL We start with the Gibbs free energy in two dimension � ���⃗����⃗� � = �′ ∫ �� �� ��[�, �] + �, (1) �� where F is the free energy given by � � ℏ � � � �[�, �] = �′ ∫ ���� � ���⃗�� + �(� − �∧)|�| + |�| �. (2) ��� � Here is the order parameter effective “thickness”, � is the order parameter describing superconductivity, �� is mass of Cooper pair, the covariant derivatives are defined by ��⃗ ≡ ��∗ ∇ + �⃗(�∗ = 2|�| is charge of Cooper pair), the vector potential describes constant and ℏ� homogeneous magnetic field �⃗ = (−��, 0). Throughout most of the paper we use the coherence length ξ as a unit of length, ∗ � ���(0) = ℏ�/� � as a unit of the magnetic field, � = ��/2�Λ� as dimensionless order parameter. The dimensionless Boltzmann factor becomes ⃗ � ���,�� � � � �(�, �) = = ∫ �� �� ����⃗�� − (1 − �Λ)|�| + |�| �, (3) � ��Λ�Λ � �� �∗ � where � = �/� , � = �2�� with �� = 2 � � ������ being the Ginzburg- � � � � � Λ �′� �ℏ Λ Landau parameter. The thermodynamic (effective) Gibbs energy [6], G t ln Z , (4) defined as dimensionless thermodynamic Gibbs energy, which determines the magnetization and Z is the partition function of the Gibbs ensemble G Z D D exp D D exp( g [ ]) . (5) T Performing the same rescaling of fields: � º�/� = �(�, �) + ����[�], where fis given in Eq. (3), b=B/Hc2 and � � �⃗ �⃗ � ����[�] = ∫ ������ − ℎ� . (6) ����� TẠP CHÍ KHOA HỌC SỐ 20/2017 89 3. MAGNETIZATION WITHIN THE SELF-CONSISTENT METHOD Magnetization in the presence of thermal fluctuation is determined from 2 G 1 * f Z D D (b h ) 0 . (7) b b2 t Taking the derivative, one obtains 1 t f m b h Z 1 D * D exp(g[ ]) . (8) 4 2 2 b Since κ 1 magnetization is small b h/ 4 2 h , and it suffices to consider a simpler statistical sum � � ≈ ∫ DΨ�Ψ∗��� �− � = ∫ DΨ�Ψ∗���(−�[Ψ]). (9) � We take f[,]KW b , which are defined below, � � � = ∫ �� �� ����⃗�� + (2� − �)|�|��, (10) ����� � � � � = ∫ �� �� [(�� + � − 1 − 2�)|�| + |�| ]. (11) ����� The thermodynamic free energy in Eq. (4) can be written as fgauss f1 W , (12) where t b f tlog D D exp( K ) log( nb ) , (13) 1 2 n 0 t b 1 b 1 b 1 2 . (14) W t 2 2 n 0nb 2 n 0 nb At large n the sums diverge, so one need to introduce an UV momentum cutoff which effectively limits the number of Landau levels to Nf / b 1. Finally, total thermodynamic free energy takes a form 2 1 1 T 1 fgauss log 1 t log 1 log 2 2 Tc 2 90 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI 1 t b 2 u'' u t u , (14) 2 1 where u'( ,t) f ( / b) log b, f is PolyGamma function, and the temperature Tc is 2 renormalized TTc 1 log , (15) 2 2 e * Note that t t, t T / T , 2 Gi , Gi 2 4 4 T 2 (T is now c2 c s s' c replaced by Tc). The gap equation is arrived by minimizing the free energy density of the system fgauss/=0 1 t b 2 tu '( , t ) (16) 2 Combining Eqs. (4), (8), (9), and (14), the average magnetization in the sample is obtained 1 f m gauss . (17) 2 2 b 4. RESULT AND DISCUSSION In order to illustrate the main features of our model, we take as example a common material, like La2-xSrxCuO4 (LSCO). Typical characteristic parameters are then: ��=24 K for the critical temperature under very small electric field and no magnetic field, = 0.1 for the o strength of thermal fluctuations, Hc2=45 T for the critical field, and s’=8A for the effective “thickness” of layer. In Fig.1 the magnetization curves computed according to Eqs. (16) and (17), are shown for different temperatures. The theoretical magnetization just below Tcis nonmonotonic, consistent withthe experiment [7,8]. Above Tc, the theoretical magnetization is still nonmonotonic, which mean that thermal fluctuation plays important role. In Fig.2, the magnetization curves computed according to Eqs. (16) and (17), are shown for different magnetic field. Our calculation show that the intersection point magnetization TẠP CHÍ KHOA HỌC SỐ 20/2017 91 curves is belowTc in wide region of magnetic field, which is consistent with experimental [6,7]. This feature cannot be explained by the mean field theory that can only be explained by theory of thermal fluctuation. Fig. 1. Magnetization as a function of magnetic field, for different temperature Fig. 2. Magnetization as a function of temperature, for different magnetic field 5. CONCLUSION We have studied effect of thermal fluctuation on magnetization of high-Tc superconductor by using the self-consistent method with Ginzburg-Landau model. Our results including all Landau levels are valid for arbitrary values of the magnetic fieldnot too close to Hc1. The method used in the present paper can also apply to strongtype II low-Tc superconductors. Our magnetization just below Tc isin fact nonmonotonic, consistent with theexperiment. Our calculation supports the phase-disorderingpicture of fluctuations advocated by La2-xSrxCuO4[9]. 92 TRƯỜNG ĐẠI HỌC THỦ ĐÔ HÀ NỘI Acknowledgment: This work was supported by the National Foundation for Science and Technology Development (NAFOSTED) of Vietnam under Grant No. 103.02-2017.316. REFERENCES 1. R. Jin,A.Schilling, and H. R.Ott (1994), Phys.Rev.B49 , p.9218. 2. U. Welpet al (1991), Phys.Rev.Lett. 67, p.3180. 3. M. J. Naughton (2000), Phys.Rev.B61, p.1605. 4. Y.M.Huh and D.K.Finnemore (2002), Phys.Rev.B 65, p.092506. 5. A.Larkin and A.Varlamov (2005), Theory of Fluctuations in Superconductors(Clarendon Press, Oxford. 6. B.Rosenstein and D.Li (2010), Rev.Mod.Phys. 82, p.109. 7. Lu Li, Y.Wang, S.Komiya, S.Ono, Y.Ando, G.D.Gu,and N.P.Ong (2010),Phys.Rev. B81, p.054510. 8. Y.Wang, LuLi, M.J.Naughton, G.D Gu, S.Uchida, and N.P.Ong (2005), Phys.Rev. Lett.95, p.247002. 9. Lu Li, Y.Wang, and N.P.Ong (2013), Phys. Rev. B 87, p.056502. ĐỘ TỪ HÓA CỦA VẬT LIỆU SIÊU DẪN NHIỆT ĐỘ CAO Tóm tắt: Chúng tôi sử dụng phương pháp tự hợp trong hình lý thuyết Ginzburg-Landau để tính toán ảnh hưởng của thăng giáng nhiệt lên độ từ hóa của vật liệu siêu dẫn nhiệt độ cao đặt trong từ trường. Kết quả thu được bao gồm tất cả các mức Landau mà có thể áp dụng cho từ trường bất kì không quá gần Hc1. Kết quả chỉ ra rằng các đường từ hóa cắt nhau và không đơn điệu dưới nhiệt độ Tc. Tính toán của chúng tôi xác nhận pha mất trật tự do thăng giáng nhiệt ở trên Tc. Từ khóa: Độ từ hóa, vật liệu siêu dẫn, từ trường, nhiệt độ cao
File đính kèm:
 magnetization_in_high_tc_superconductors.pdf
magnetization_in_high_tc_superconductors.pdf

