Large displacements of fgsw beams in thermal environment using a finite element formulation
Abstract. The large displacements of functionally graded sandwich (FGSW) beams in
thermal environment are studied using a finite element formulation. The beams are composed of three layers, a homogeneous core and two functionally graded face sheets with
volume fraction of constituents following a power gradation law. The material properties of the beams are considered to be temperature-dependent. Based on Antman beam
model and the total Lagrange formulation, a two-node nonlinear beam element taking the
effect of temperature rise into account is formulated and employed in the study. The element with explicit expressions for the internal force vector and tangent stiffness matrix is
derived using linear interpolations and reduced integration technique to avoid the shear
locking. Newton-Raphson based iterative algorithm is employed in combination with
the arc-length control method to compute the large displacement response of a cantilever
FGSW beam subjected to end forces. The accuracy of the formulated element is confirmed
through a comparison study. The effects of the material inhomogeneity, temperature rise
and layer thickness ratio on the large deflection response of the beam are examined and
highlighted.

Trang 1

Trang 2

Trang 3

Trang 4
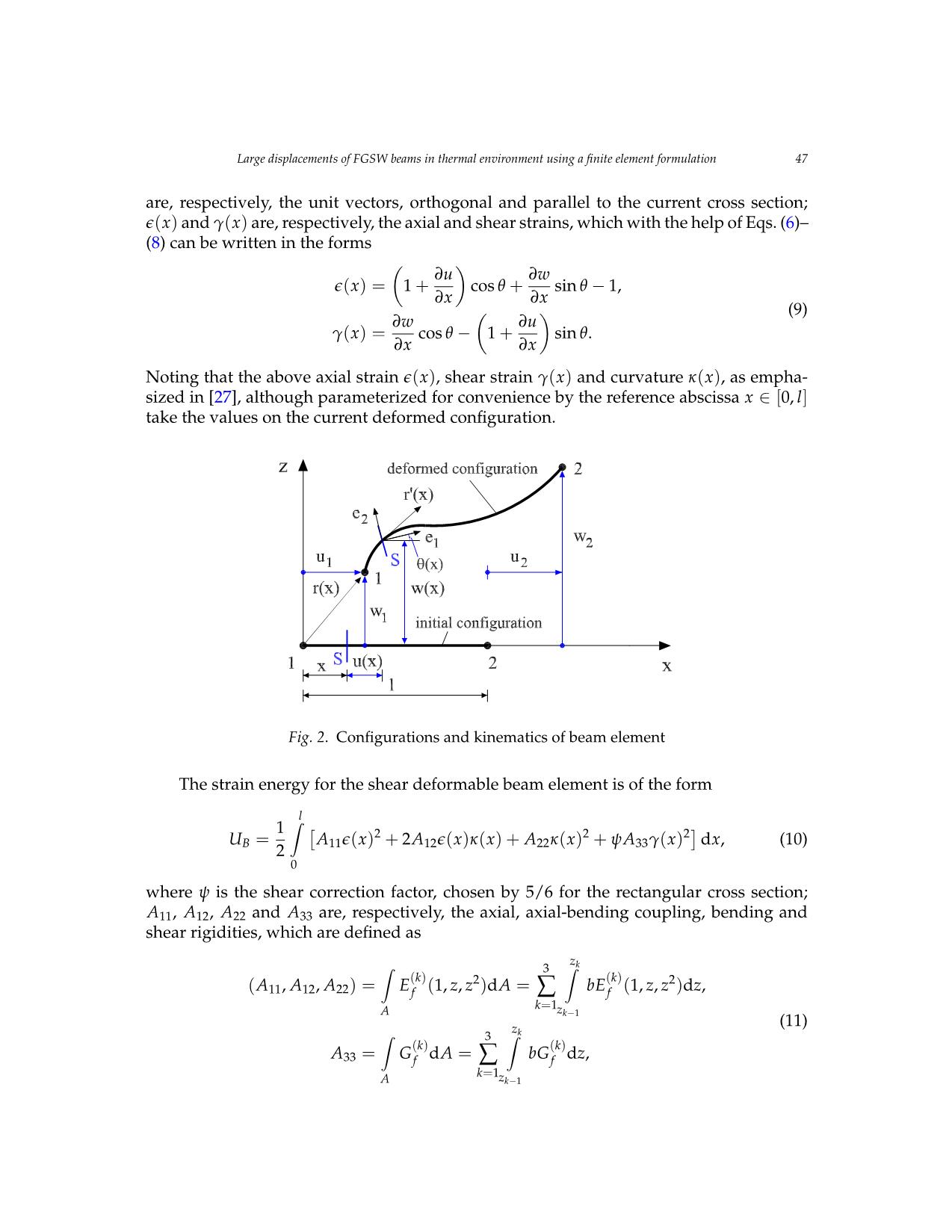
Trang 5

Trang 6

Trang 7
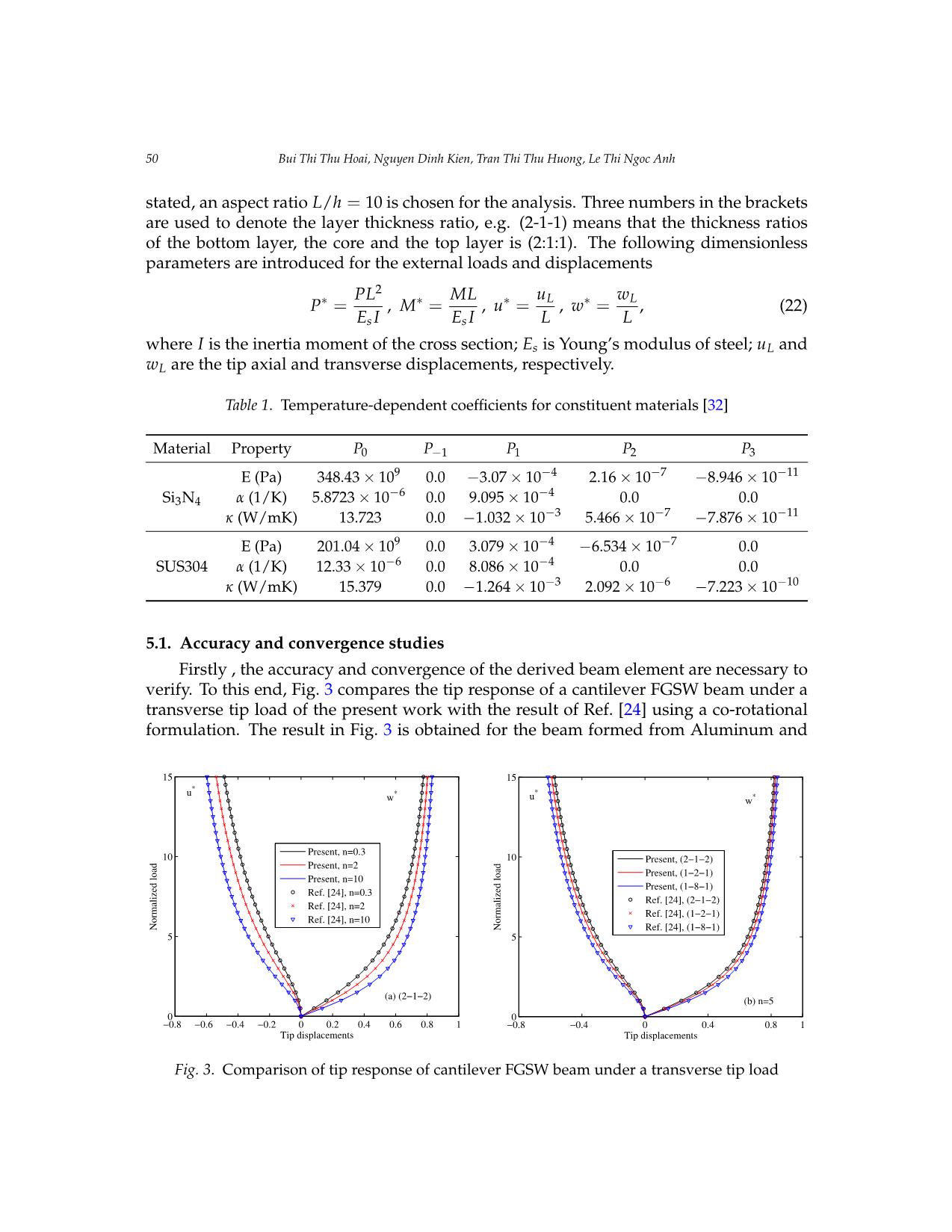
Trang 8
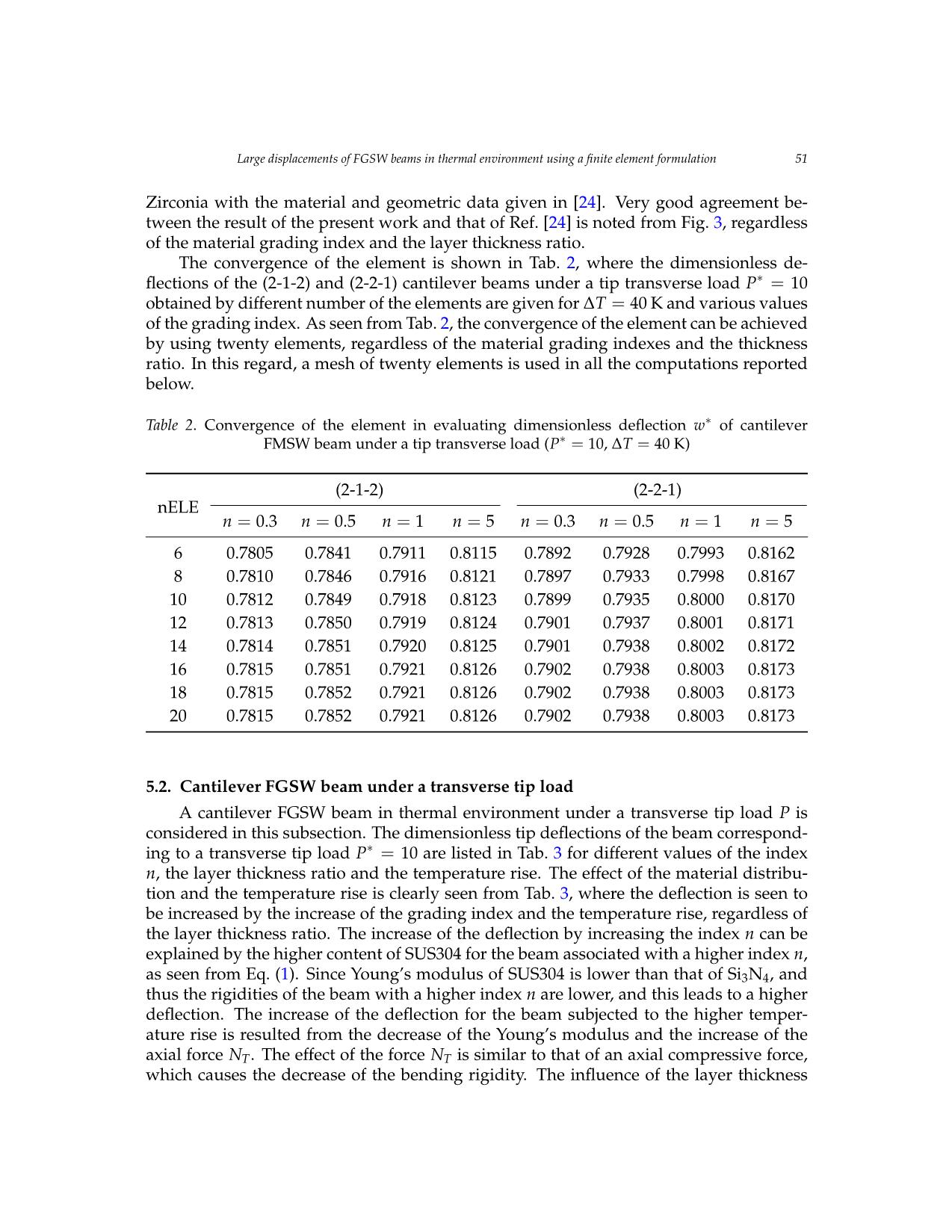
Trang 9
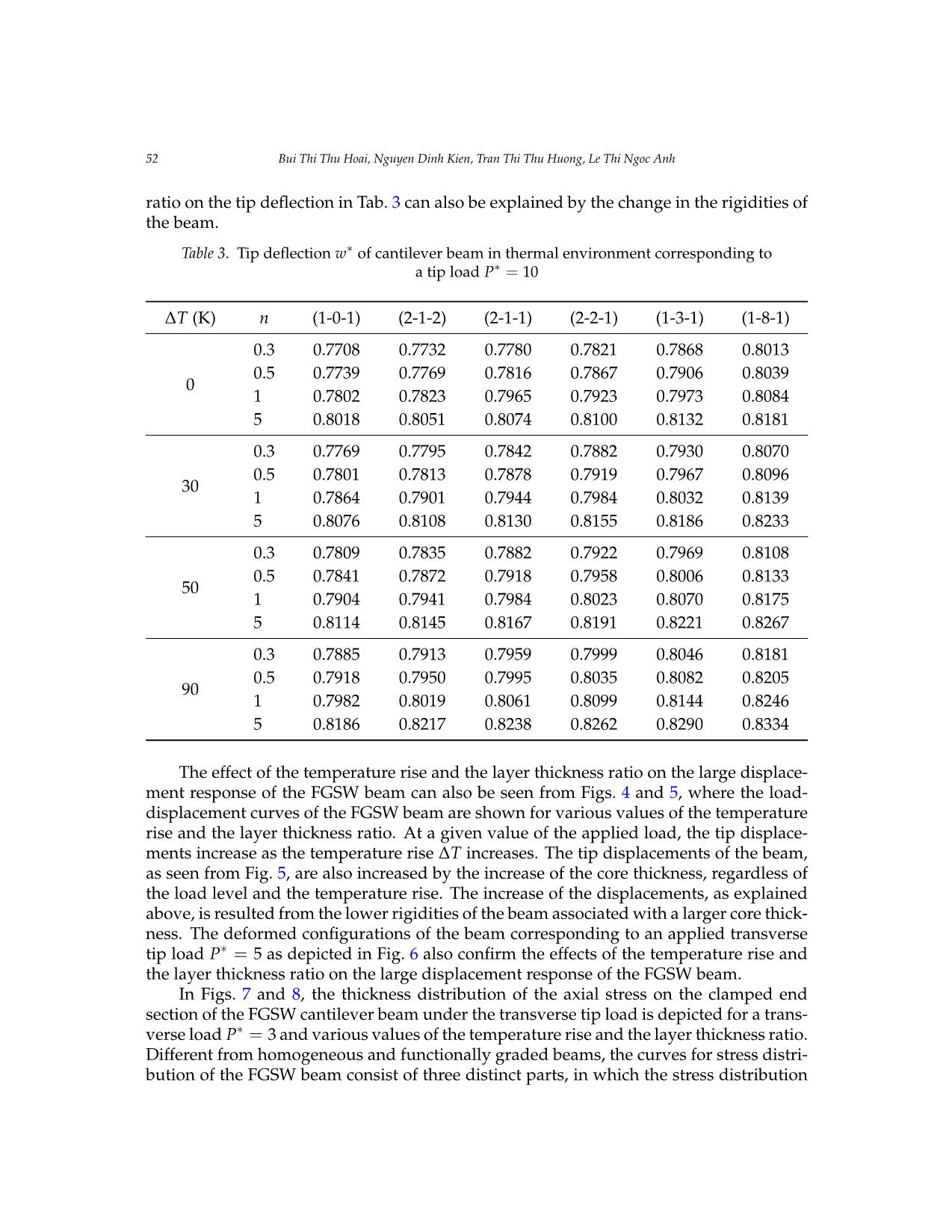
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Large displacements of fgsw beams in thermal environment using a finite element formulation

Vietnam Journal of Mechanics, VAST, Vol.42, No. 1 (2020), pp. 43 – 61
DOI: https://doi.org/10.15625/0866-7136/14628
LARGE DISPLACEMENTS OF FGSW BEAMS
IN THERMAL ENVIRONMENT USING A FINITE ELEMENT
FORMULATION
Bui Thi Thu Hoai1,2,∗, Nguyen Dinh Kien1,2, Tran Thi Thu Huong3, Le Thi Ngoc Anh4
1Institute of Mechanics, VAST, Hanoi, Vietnam
2Graduate University of Science and Technology, VAST, Hanoi, Vietnam
3Phenikaa University, Hanoi, Vietnam
4Institute of Applied Mechanics and Informatics, VAST, Ho Chi Minh city, Vietnam
E-mail: thuhoaihus@gmail.com
Received: 18 December 2019 / Published online: 20 March 2020
Abstract. The large displacements of functionally graded sandwich (FGSW) beams in
thermal environment are studied using a finite element formulation. The beams are com-
posed of three layers, a homogeneous core and two functionally graded face sheets with
volume fraction of constituents following a power gradation law. The material proper-
ties of the beams are considered to be temperature-dependent. Based on Antman beam
model and the total Lagrange formulation, a two-node nonlinear beam element taking the
effect of temperature rise into account is formulated and employed in the study. The ele-
ment with explicit expressions for the internal force vector and tangent stiffness matrix is
derived using linear interpolations and reduced integration technique to avoid the shear
locking. Newton-Raphson based iterative algorithm is employed in combination with
the arc-length control method to compute the large displacement response of a cantilever
FGSW beam subjected to end forces. The accuracy of the formulated element is confirmed
through a comparison study. The effects of the material inhomogeneity, temperature rise
and layer thickness ratio on the large deflection response of the beam are examined and
highlighted.
Keywords: FGSW beam, total Lagrange formulation, reduced integration, thermal environ-
ment, large deflection analysis.
1. INTRODUCTION
Large displacement analysis of structures has drawn much attention from researchers
since the recent invention of new materials allows structures to undergo large deforma-
tion during their service. The finite element method, a powerful tool in solving nonlinear
problems, is a preferable choice in dealing with this problem. In the context of finite
element analysis, two types of nonlinear formulation for analyzing beams undergoing
large displacement, namely the co-rotational formulation [1,2] and the total Lagrange
c 2020 Vietnam Academy of Science and Technology
44 Bui Thi Thu Hoai, Nguyen Dinh Kien, Tran Thi Thu Huong, Le Thi Ngoc Anh
one [3,4], are the most often used. The main difference between these two formulations
is the choice of reference frames, which leads to different expressions of the element for-
mulation.
Functionally graded materials (FGMs), a new type of composites initiated by Japan-
ese scientists in mid-1980 [5], are increasing used to fabricate structural elements for use
in severe environment. Investigations on nonlinear behaviour of FGM beam structure
have been extensively reported in the last two decades. In this line of works, Kang and
Li [6,7] derived the large displacement solutions for cantilever FGM beams subjected to
a transverse tip load or a tip moment. The position of the neutral axis has been taken into
account in the derivation, which eliminates the axial deformation and bending coupling
effect. Kocaturk¨ et al. [8] formulated a total Lagrange formulation for studying large
displacement behaviour of FGM beams due to distributed load. Also using the total La-
grange formulation, Almeida et al. [9] investigated geometrically nonlinear behaviour of
FGM beams under mechanical loads. Levyakov [10, 11] adopted the neutral surface as
reference plane to derive the elastic solutions for FGM beams under the thermal loading.
Based on the third-order shear deformation beam theory, Zhang [12] derived the consti-
tutive equations for studying the nonlinear bending of FGM beams. Nguyen et al. [13–17]
derived the co-rotational beam elements for large displacement analysis of FGM beams
and frames. The effect of plastic deformation on buckling and nonlinear bending of FGM
beams is considered using the finite element method [18,19]. A geometrically exact beam
model with fully intrinsic formulation is employed by Masjedi et al. [20] to study the
large deflection behaviour of functionally graded beams under conservative and non-
conservative loading.
With the development of advanced manufacturing methods [21], FGMs can now be
incorporated into sandwich construction to improve the performance of structures. Func-
tionally graded sandwich (FGSW) structures can be designed to have a smooth variation
of material properties, and this helps to avoid the interface delaminating problem as often
seen in the conventional sandwich structures. Several investigations, mainl ... 25 −0.25
*
(a) (2−1−1), n=3, P =3 (b) (1−2−1), n=3, P*=3
−0.5 −0.5
−1.2 −0.8 −0.4 0 0.4 0.8 1 −1.2 −0.8 −0.4 0 0.4 0.8 1.2
σ /109 (N/m) σ /109 (N/m)
x x
Fig. 7. Effect of temperature rise on thickness distribution of axial stress at clamped section
of FGSW cantilever beam corresponding to a transverse tip load P∗ = 3
Large displacements of FGSW beams in thermal environment using a finite element formulation 55
0.5 0.5
(1−0−1) (1−0−1)
(2−2−1) (2−2−1)
(1−8−1) (1−8−1)
0.25 0.25
0
z/h 0
z/h
−0.25 −0.25
*
(a) n=3, ∆T=0, P =3 (b) n=3, ∆T=50K, P*=3
−0.5 −0.5
−1.2 −0.8 −0.4 0 0.4 0.8 1.2 −1.2 −0.8 −0.4 0 0.4 0.8 1.2
9
σ /10 (N/m) σ /109 (N/m)
x x
Fig. 8. Effect of layer thickness ratio on thickness distribution of axial stress at clamped section
of FGSW cantilever beam corresponding to a transverse tip load P∗ = 3
5.3. Roll-up of cantilever beam due to a tip moment
The roll-up of a cantilever FGSW beam subjected to a tip moment M is studied in this
sub-section. In Figs.9 and 10, the equilibrium paths of the beam are respectively depicted
for different values of the temperature rise and the layer thickness ratio. The temperature
rise and the layer thickness ratio, as seen from the figures, play an important role on the
large displacement behaviour of the beam. The effect of the layer thickness ratio on the
response of the beam is more significant in the large displacement region than that of
6 6
* *
u* w* u w
5 5
4 4
3 3
Normalized moment
2 Normalized moment 2
(a) n=5, ∆T=50K (b) n=5, ∆T=90K
∆ T=0K ∆ T=0K
1 ∆ T=30K 1 ∆ T=30K
∆ T=60K ∆ T=60K
∆ T=90K ∆ T=90K
0 0
−1.5 −1 −0.5 0 0.5 1 −1.5 −1 −0.5 0 0.5 1
Tip displacements Tip displacements
Fig. 9. Equilibrium paths of cantilever FGSW beam under a tip moment
for different temperature rise
56 Bui Thi Thu Hoai, Nguyen Dinh Kien, Tran Thi Thu Huong, Le Thi Ngoc Anh
6 6
* *
u w u* w*
5 5
4 4
3 3
Normalized moment
2 Normalized moment 2
(a) n=5, ∆ T=50K (b) n=5 ∆ T=90K
(8−1−8) (8−1−8)
1 (2−2−1) 1 (2−2−1)
(1−3−1) (1−3−1)
(1−8−1) (1−8−1)
0 0
−1.5 −1 −0.5 0 0.5 1 −1.5 −1 −0.5 0 0.5 1
Tip displacements Tip displacements
Fig. 10. Equilibrium paths of cantilever FGSW beam under a tip moment
for different layer thickness ratio
0.4 0.4
0.3 0.3
0.2 ∆T=0K 0.2
w*
w* (1−0−1)
∆T=50K (2−1−1)
∆T=90K (1−8−1)
*
0.1 (a) (2−1−1), n=2, M*=7 0.1 (b) n=5, ∆T=50K, M =7
0 0
−0.2 −0.1 0 0.1 0.2 −0.2 −0.1 0 0.1 0.2
x/L x/L
Fig. 11. Deformed configurations of FGSW beam subjected to a tip moment
the temperature rise. The significant influence of the layer thickness ratio on the large
displacement behaviour of the FGSW beam can be seen more clearly from Fig. 11, where
the deformed configurations of the beam are displayed for M∗ = 7 and different values
of the temperature rise and layer thickness ratio. At the applied moment M∗ = 7, the
(1-8-1) beam has already rolled up to a circle while the (1-0-1) beam has not yet. Noting
that due to the snap-back of the equilibrium paths, the arc-length control method must
be employed to trace the paths in Figs.9 and 10.
Large displacements of FGSW beams in thermal environment using a finite element formulation 57
6. CONCLUSIONS
The large displacement behaviour of FGSW beams in thermal environment has been
investigated by a finite element formulation. The beams are considered to be composed
of three layers, a homogeneous core and two functionally graded skin layers with the
temperature-dependent material properties. Based on the Antman beam model, a first-
order shear deformable nonlinear beam element taking the effect of temperature rise into
account was formulated in the context of the total Lagrange formulation. The element
with explicit expressions for the internal force vector and tangent stiffness matrix has
been derived using the reduced integration technique to avoid the shear locking. Using
the derived beam element, the large displacement response of a cantilever FGSW beam
under the end forces has been computed, and the effects of the material inhomogeneity,
temperature rise and layer thickness ratio have been examined. The obtained numerical
results reveal that, in addition to the material inhomogeneity, the temperature rise and
the layer thickness ratio also play an important role on the large displacement behaviour
of the beam. It has been shown that the effect of the layer thickness ratio on the behaviour
of the FGSW beams in the large displacement region is more significant than that of the
temperature rise. It is necessary to note that though the numerical investigation in the
present paper has been carried out for the cantilever beam only, the element formulation
formulated herein can be used to analyze the FGSW beams with other boundary con-
ditions as well. Additionally, the present beam formulation is simple, and its extension
to the large displacement analysis of beams made of other materials, e.g., functionally
graded carbon nanotube reinforced composite beams, is straightforward.
ACKNOWLEDGEMENTS
The work presented in this article was supported by National Foundation for Science
and Technology Development (NAFOSTED), grant number 107.02-2018.23 and Vietnam
Academy of Science and Technology, grant number QTRU01.07/20-21.
REFERENCES
[1] D. K. Nguyen. A non-linear element for analysing elastic frame structures at large deflec-
tions. Vietnam Journal of Mechanics, 22, (1), (2000), pp. 19–28. https://doi.org/10.15625/0866-
7136/9959.
[2] D. K. Nguyen and Q. Q. Do. Large deflection analysis of frames by elements con-
taining higher-order terms. Vietnam Journal of Mechanics, 25, (4), (2003), pp. 243–254.
https://doi.org/10.15625/0866-7136/25/4/6595.
[3] R. D. Wood and O. C. Zienkiewicz. Geometrically nonlinear finite element analysis of beams,
frames, arches and axisymmetric shells. Computers & Structures, 7, (6), (1977), pp. 725–735.
https://doi.org/10.1016/0045-7949(77)90027-x.
[4] D. K. Nguyen. Postbuckling behavior of beams on two-parameter elastic foundation.
International Journal of Structural Stability and Dynamics, 4, (01), (2004), pp. 21–43.
https://doi.org/10.1142/s0219455404001082.
[5] M. Koizumi. FGM activities in Japan. Composites Part B: Engineering, 28, (1-2), (1997), pp. 1–4.
https://doi.org/10.1016/s1359-8368(96)00016-9.
58 Bui Thi Thu Hoai, Nguyen Dinh Kien, Tran Thi Thu Huong, Le Thi Ngoc Anh
[6] Y. A. Kang and X. F. Li. Bending of functionally graded cantilever beam with power-law
non-linearity subjected to an end force. International Journal of Non-Linear Mechanics, 44, (6),
(2009), pp. 696–703. https://doi.org/10.1016/j.ijnonlinmec.2009.02.016.
[7] Y. A. Kang and X. F. Li. Large deflections of a non-linear cantilever functionally
graded beam. Journal of Reinforced Plastics and Composites, 29, (12), (2010), pp. 1761–1774.
https://doi.org/10.1177/0731684409103340.
[8] T. Kocaturk,¨ M. S¸ims¸ek, and S¸. D. Akbas¸. Large displacement static analysis of a cantilever
Timoshenko beam composed of functionally graded material. Science and Engineering of Com-
posite Materials, 18, (1-2), (2011), pp. 21–34. https://doi.org/10.1515/secm.2011.005.
[9] C. A. Almeida, J. C. R. Albino, I. F. M. Menezes, and G. H. Paulino. Geomet-
ric nonlinear analyses of functionally graded beams using a tailored Lagrangian
formulation. Mechanics Research Communications, 38, (8), (2011), pp. 553–559.
https://doi.org/10.1016/j.mechrescom.2011.07.006.
[10] S. V. Levyakov. Elastica solution for thermal bending of a functionally graded beam. Acta
Mechanica, 224, (8), (2013), pp. 1731–1740. https://doi.org/10.1007/s00707-013-0834-1.
[11] S. V. Levyakov. Thermal elastica of shear-deformable beam fabricated of functionally graded
material. Acta Mechanica, 226, (3), (2015), pp. 723–733. https://doi.org/10.1007/s00707-014-
1218-x.
[12] D. G. Zhang. Nonlinear bending analysis of FGM beams based on physical neutral sur-
face and high order shear deformation theory. Composite Structures, 100, (2013), pp. 121–126.
https://doi.org/10.1016/j.compstruct.2012.12.024.
[13] D. K. Nguyen. Large displacement response of tapered cantilever beams made of axi-
ally functionally graded material. Composites Part B: Engineering, 55, (2013), pp. 298–305.
https://doi.org/10.1016/j.compositesb.2013.06.024.
[14] D. K. Nguyen. Large displacement behaviour of tapered cantilever Euler–Bernoulli beams
made of functionally graded material. Applied Mathematics and Computation, 237, (2014),
pp. 340–355. https://doi.org/10.1016/j.amc.2014.03.104.
[15] D. K. Nguyen, T. H. Trinh, and T. H. Le. A co-rotational beam element for geometrically
nonlinear analysis of plane frames. Vietnam Journal of Mechanics, 35, (1), (2013), pp. 51–65.
https://doi.org/10.15625/0866-7136/35/1/2892.
[16] D. K. Nguyen and B. S. Gan. Large deflections of tapered functionally graded beams sub-
jected to end forces. Applied Mathematical Modelling, 38, (11-12), (2014), pp. 3054–3066.
[17] D. K. Nguyen, B. S. Gan, and T. H. Trinh. Geometrically nonlinear analysis of planar beam
and frame structures made of functionally graded material. Structural Engineering and Me-
chanics, 49, (6), (2014), pp. 727–743. https://doi.org/10.12989/sem.2014.49.6.727.
[18] T. H. Trinh, D. K. Nguyen, B. S. Gan, and S. Alexandrov. Post-buckling responses of elasto-
plastic FGM beams on nonlinear elastic foundation. Structural Engineering and Mechanics, 58,
(3), (2016), pp. 515–532. https://doi.org/10.12989/sem.2016.58.3.515.
[19] D. K. Nguyen, K. V. Nguyen, B. S. Gan, and S. Alexandrov. Nonlinear bend-
ing of elastoplastic functionally graded ceramic-metal beams subjected to nonuni-
form distributed loads. Applied Mathematics and Computation, 333, (2018), pp. 443–459.
https://doi.org/10.1016/j.amc.2018.03.100.
[20] P. K. Masjedi, A. Maheri, and P. M. Weaver. Large deflection of functionally graded porous
beams based on a geometrically exact theory with a fully intrinsic formulation. Applied Math-
ematical Modelling, 76, (2019), pp. 938–957. https://doi.org/10.1016/j.apm.2019.07.018.
Large displacements of FGSW beams in thermal environment using a finite element formulation 59
[21] Y. Watanabe, Y. Inaguma, H. Sato, and E. Miura-Fujiwara. A novel fabrication method
for functionally graded materials under centrifugal force: The centrifugal mixed-powder
method. Materials, 2, (4), (2009), pp. 2510–2525. https://doi.org/10.3390/ma2042510.
[22] T. P. Vo, H. T. Thai, T. K. Nguyen, A. Maheri, and J. Lee. Finite element
model for vibration and buckling of functionally graded sandwich beams based on
a refined shear deformation theory. Engineering Structures, 64, (2014), pp. 12–22.
https://doi.org/10.1016/j.engstruct.2014.01.029.
[23] T. P. Vo, H. T. Thai, T. K. Nguyen, F. Inam, and J. Lee. A quasi-3D theory for vibration and
buckling of functionally graded sandwich beams. Composite Structures, 119, (2015), pp. 1–12.
https://doi.org/10.1016/j.compstruct.2014.08.006.
[24] D. K. Nguyen and T. T. Tran. A corotational formulation for large displacement analysis of
functionally graded sandwich beam and frame structures. Mathematical Problems in Engineer-
ing, 2016, (2016). https://doi.org/10.1155/2016/5698351.
[25] Y. S. Touloukian. Thermophysical properties of high temperature solid materials. Macmillan, New
York, USA, (1967).
[26] S. S. Antman. Nonlinear problems of elasticity. Springer-Verlag, New York, (1995).
[27] C. Pacoste and A. Eriksson. Beam elements in instability problems. Computer Methods in Ap-
plied Mechanics and Engineering, 144, (1-2), (1997), pp. 163–197. https://doi.org/10.1016/s0045-
7825(96)01165-6.
[28] E. N. Lages, G. H. Paulino, I. F. M. Menezes, and R. R. Silva. Nonlinear finite el-
ement analysis using an object-oriented philosophy–application to beam elements and
to the cosserat continuum. Engineering with Computers, 15, (1), (1999), pp. 73–89.
https://doi.org/10.1007/s003660050006.
[29] A. Mahi, E. A. A. Bedia, A. Tounsi, and I. Mechab. An analytical method for
temperature-dependent free vibration analysis of functionally graded beams with
general boundary conditions. Composite Structures, 92, (8), (2010), pp. 1877–1887.
https://doi.org/10.1016/j.compstruct.2010.01.010.
[30] R. D. Cook, D. S. Malkus, and M. E. Plesha. Concepts and applications of finite element analysis.
John Wiley & Sons, New York, USA, 3rd edition, (1989).
[31] M. A. Crisfield. Non-linear finite element analysis of solids and structures, Vol. 1: Essentials. John
Wiley & Sons, Chichester, (1991).
[32] H. S. Shen and Z. X. Wang. Nonlinear analysis of shear deformable FGM beams resting on
elastic foundations in thermal environments. International Journal of Mechanical Sciences, 81,
(2014), pp. 195–206. https://doi.org/10.1016/j.ijmecsci.2014.02.020.
60 Bui Thi Thu Hoai, Nguyen Dinh Kien, Tran Thi Thu Huong, Le Thi Ngoc Anh
APPENDIX
This Appendix presents detail expressions for the nodal forces and the tangent stiff-
ness matrices in Eq. (19). The following notations are used
s = sin θ¯ , c = cos θ¯,
2
a1 = (sε¯ − cγ¯) , a2 = (cε¯ + sγ¯) , a3 = γ¯ − ε¯ (1 + ε¯) , (23)
2 2
a4 = cγ¯ − s (1 + ε¯) , a5 = sγ¯ + c (1 + ε¯) , a6 = (1 + ε¯) − γ¯ .
The internal force vector
l l T
f = A ε¯ −c − s γ¯ c s γ¯ , f = A κ¯{0 0 1 0 0 − 1}T,
a 11 2 2 b 22
l l T
f = A ε¯{0 0 1 0 0 − 1}T + A κ¯ −c − s γ¯ c s γ¯ ,
c 12 12 2 2
(24)
l l T
f = ψA γ¯ s − c − (1 + ε¯) − s c − (1 + ε¯) ,
s 33 2 2
(w − w ) (w − w ) T
f = 0 − 2 1 N 0 0 2 1 N 0 ,
T l T l T
c2
sc s2 sym.
2
l l l
a1 − a2 a3
2 2 4
1 l
ka = A 2 2 , (25)
l 11 −c −sc − a1 c
2
l
− − 2 2
sc s a5 sc s
2
l l l2 l l l2
a − a a − a a a
2 1 2 2 4 3 2 1 2 2 4 3
0
0 0 sym.
1 0 0 1
k = A , (26)
b l 22 0 0 0 0
0 0 0 0 0
0 0 −1 0 0 1
Large displacements of FGSW beams in thermal environment using a finite element formulation 61
0 0 s 0 0 s 0 0 −c 0 0 c
0 0 −c 0 0 −c 0 0 −s 0 0 s
s c l s c l l l
− − (1 + ε¯) − (1 + ε¯) 0 0 γ¯ 0 0 − γ¯
2 2 2 2 2 2 2 2 2
kc = A12κ¯ + A12 ,
0 0 −s 0 0 −s l 0 0 c 0 0 −c
0 0 c 0 0 c 0 0 s 0 0 −s
1 1 l 1 1 l l l
s − c − (1 + ε¯) − s c (1 + ε¯) 0 0 γ¯ 0 0 − γ¯
2 2 2 2 2 2 2 2
(27)
s2
−sc c2 sym.
2
l l l
a4 a5 a6
2 2 4
ψ l
ks = A33 2 2 , (28)
l −s sc − a4 s
2
l
− 2 − − 2
sc c a5 sc c
2
l l l2 l l l2
a a a − a − a a
2 4 2 5 4 6 2 4 2 5 4 6
0
0 1 sym.
0 0 0
NT
k = . (29)
T l 0 0 0 0
0 −1 0 0 1
0 0 0 0 0 0
File đính kèm:
 large_displacements_of_fgsw_beams_in_thermal_environment_usi.pdf
large_displacements_of_fgsw_beams_in_thermal_environment_usi.pdf

