Hydrodynamic and dynamic analysis to determine the longitudinal hydrodynamic coefficients of an autonomous underwater vehicle

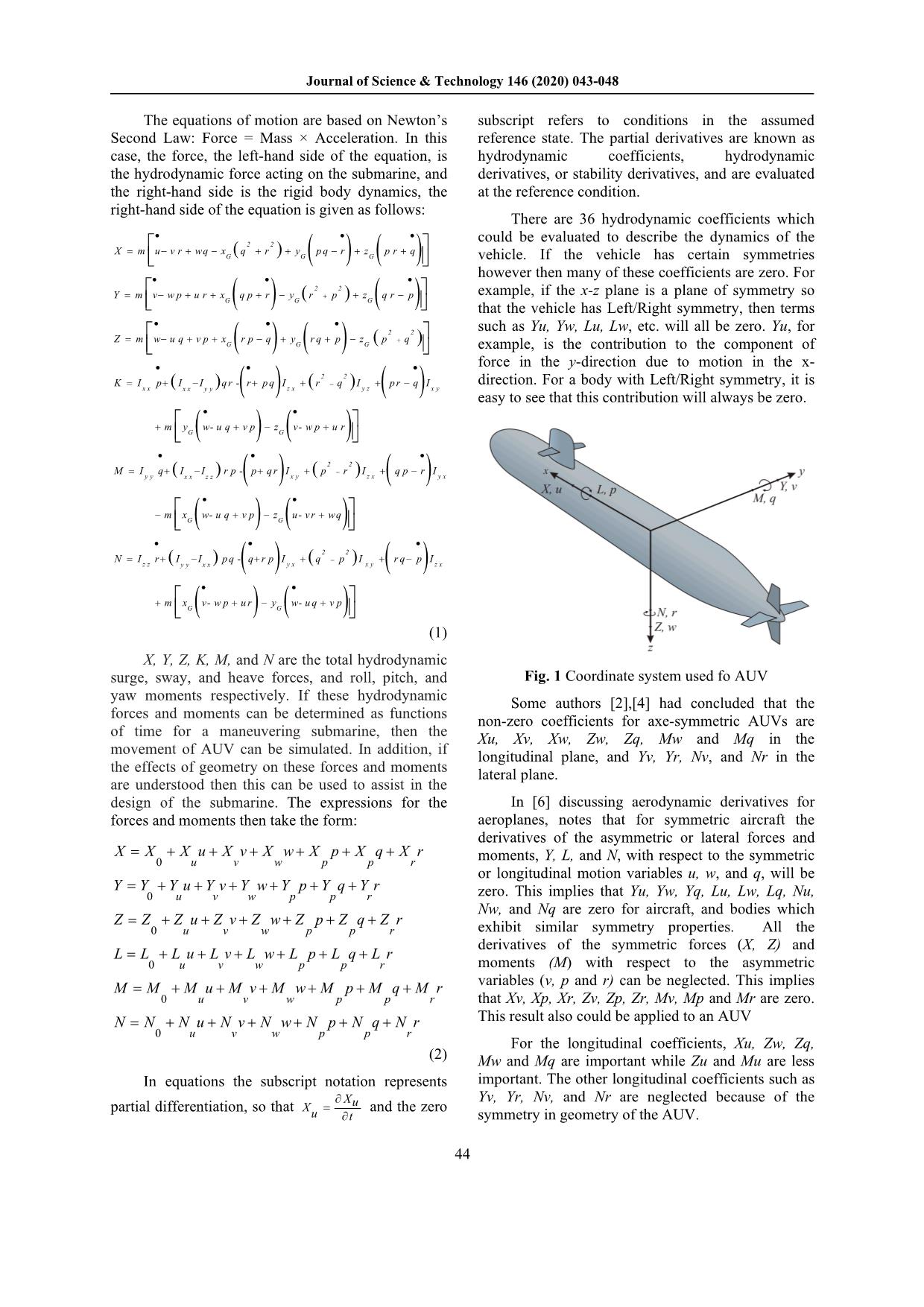
 Journal of Science & Technology 146 (2020) 043-048 
 Hydrodynamic and Dynamic Analysis to Determine the Longitudinal 
 Hydrodynamic Coefficients of an Autonomous Underwater Vehicle 
 Le Quang*, Phan Anh Tuan, Pham Thi Thanh Huong 
 Hanoi University of Science and Technology, No. 1, Dai Co Viet, Hai Ba Trung, Hanoi, Viet Nam 
 Received: June 07, 2020; Accepted: November 12, 2020 
 Abstract 
 A useful tool for understanding the performance of an Autonomous Underwater Vehicle (AUV) is a dynamic 
 simulation of the motions of the vehicle. To perform the simulation, the hydrodynamic coefficients of the 
 vehicle must be first provided. These coefficients are specific to the vehicle and provide the description of 
 hydrodynamic forces and moments acting on the vehicle in an underwater environment. This paper provides 
 a method for the calculation and evaluation of the hydrodynamic coefficients of an AUV. The presence 
 methodology is therefore one useful tool for determining an underwater vehicle’s dynamic stability. The 
 calculated values have been compared with experimental results of a torpedo shape. It was concluded that 
 the methods could calculate accurate values of the hydrodynamic coefficients for a specific AUV shape with 
 its elliptical nose 
 Keywords: Stability, Autonomous Underwater Vehicles (AUV), simulation, hydrodynamic coefficients 
1. Introduction* 
 This paper shows the results by using the semi-
 During the underwater vehicle scheme design experimental method (used U.S Air Force DATCOM 
period, the simulation and evaluation of the stability method). This method is based on the techniques 
of submarine is an important task. Simulation of the developed in the aeronautical industry. The calculated 
motion of an underwater vehicle requires the values were then compared with CFD results and 
numerical solution of six-coupled non-linear other data available [2]. 
differential equations. Three of these equations 
 2. Equation of AUV Motion 
describe the translational motions of the vehicle, the 
remaining three equations describe rotational The equations of motion for a submarine are 
motions of the vehicle about some fixed point on the similar to those for an aircraft, they include all six 
body [1]. This fixed point is usually taken degrees of freedom [1],[5],[7]. For a submarine, it is 
to be either the centre of mass (CM) or the centre of normal to take the origin as the longitudinal centre of 
buoyancy (CB) of the vehicle. Detailed derivations gravity (LCG), rather than midships, as this simplifies 
and discussions of these equations of motion can be the equations, and for a submarine, this position is 
found in many references [2], [3]. Traditionally, the fixed (unlike for a surface ship). The axis system used 
methods to predict the hydrodynamic derivatives of is shown in the notation in Table 1. 
underwater vehicles could be classified into three 
types: the semi-empirical method, the potential flow Table 1. Notation 
method, and the captive-model experiments including Position Velocity Force/Moment 
the oblique towing tests, the rotating arm experiments 
and the Planar Motion Mechanism (PMM) [1]. Surge x u X 
 With the semi-empirical method, the Sway y v Y 
complicated underwater vehicle shape usually could 
 Heave z w Z 
not be taken into full account. The potential theory 
could predict the inertial hydrodynamic coefficients Roll φ p K 
satisfactorily, but with the viscous terms neglected 
[3]. The PMM experiment may be the most effective Pitch θ q M 
way, but it requires special facilities and equipment 
 Yaw ψ r N 
and it is both time-consuming and costly [3], as not 
economical at the preliminary design stage. Appendage δ 
 Propulsion n 
*Corresponding author: Tel.: (+84) 913.223.160 
Email: quang.le@hust.edu.vn 
 43 
 Journal of Science & Technology 146 (2020) 043-048 
 The equations of motion are based on Newton’s subscript refers to conditions in the assumed 
Second Law: Force = Mass × Acceleration. In this reference state. The partial derivatives are known as 
case, the force, the left-hand side of the equation, is hydrodynamic coefficients, hydrodynamic 
the hydrodynamic force acting on the submarine, and derivatives, or stability derivatives, and are evaluated 
the right-hand side is the rigid body dynamics, the at the reference condition. 
right-hand side of the equation is given as follows: 
 There are 36 hydrodynamic coefficients which 
 • ••
 22 could be evaluated to describe the dynamics of the 
 X=−+−++−++ m u v r wq x( q r) y pq r z p r q
 G GG( ) ( ) vehicle. If the vehicle has certain symmetries 
 •• •however then many of these coefficients are zero. For 
 22
 Y= m v − wp + ur + x qp +− r y( r+ p) + z qr − p example, if the x-z plane is a plane of symmetry so 
 GG G
 ( ) ( ) that the vehicle has Left/Right symmetry, then terms 
 • ••
 22 such as Yu, Yw, Lu, Lw, etc. will all be zero. Yu, for 
 Z= mwuqvpx − ++ rpqy −+ rqp + − z( p+ q)
 G( ) GG( ) example, is the contribution to the component of 
 •• •force in the y-direction due to motion in the x-
 22
 K= I p +−( I I) qr - r + pq I +( r− q) I +− pr q I direction. For a body with Left/Right symmetry, it is 
 xx xx yy ( ) zx yz ( ) xy
 easy to see that this contribution will always be zero. 
 ••
 +m y w-uq +− vp z v-wp + ur
 GG( ) ( )
 •• •
 22
 MI= q+−( I I) rp-p + qrI +( p− r) I +− qprI
 y y xx zz ( ) xy zx ( ) yx
 ••
 −m x w- u q +− v p z u- vr + wq
 GG( ) ( )
 •• •
 22
 N= I r +( I − I) pq-qrpI + +( q− p) I+− rqpI
 zz yy xx ( ) yx xy ( ) zx
 ••
 +m x v- wp +− ur y w-uq + vp
 GG( ) ( )
 (1) 
 X, Y, Z, K, M, and N are the total hydrodynamic 
surge, sway, and heave forces, and roll, pitch, and Fig. 1 Coordinate system used fo AUV 
yaw moments respectively. If these hydrodynamic 
 Some authors [2],[4] had concluded that the 
forces and moments can be determined as functions 
 non-zero coefficients for axe-symmetric AUVs are 
of time for a maneuvering submarine, then the Xu, Xv, Xw, Zw, Zq, Mw and Mq in the 
movement of AUV can be simulated. In addition, if longitudinal plane, and Yv, Yr, Nv, and Nr in the 
the effects of geometry on these forces and moments lateral plane. 
are understood then this can be used to assist in the 
design of the submarine. The expressions for the In [6] discussing aerodynamic derivatives for 
forces and moments then take the form: aeroplanes, notes that for symmetric aircraft the 
 derivatives of the asymmetric or lateral forces and 
 X=+++ X XuXvXwXpXqXr + + +
 0 uvw p pr moments, Y, L, and N, with respect to the symmetric 
 or longitudinal motion variables u, w, and q, will be 
 Y=+++ Y YuYvYwYpYqYr + + +
 0 uvw p pr zero. This implies that Yu, Yw, Yq, Lu, Lw, Lq, Nu, 
 Nw, and Nq are zero for aircraft, and bodies which 
 Z=+++ Z ZuZvZwZpZqZr + + +
 0 uvw p pr exhibit similar symmetry properties. All the 
 derivatives of the symmetric forces (X, Z) and 
 L=+++ L LuLvLwLpLqLr + + +
 0 uvw p pr moments (M) with respect to the asymmetric 
 variables (v, p and r) can be neglected. This implies 
 M=+++ M MuMvMwMpMqMr + + +
 0 uvw p pr that Xv, Xp, Xr, Zv, Zp, Zr, Mv, Mp and Mr are zero. 
 N=+++ N NuNvNwNpNqNr + + + This result also could be applied to an AUV 
 0 uvw p pr
 For the longitudinal coefficients, Xu, Zw, Zq, 
 (2) Mw and Mq are important while Zu and Mu are less 
 In equations the subscript notation represents important. The other longitudinal coefficients such as 
 ∂ X Yv, Yr, Nv, and Nr are neglected because of the 
partial differentiation, so that X = u and the zero 
 u ∂t symmetry in geometry of the AUV. 
 44 
 Journal of Science & Technology 146 (2020) 043-048 
3. Determination of hydrodynamic coefficients S
 ' = − b
 ZCq,B L (7) 
 In the present work, the hydrodynamic stability l2 q,β
derivatives are determined through DATCOM 
method [3], combined with CFD simulation. Peterson 3.4 Calculation of M' : The pitching 
uses the DATCOM method for the calculation of the q,B
 '' ' moment/pitch rate curve slope [2]: 
hydrodynamic coefficients ZMwB,,;; wB ZqB, and 
 ' ' ' 2
 M qB, for the bare hull, and ZwB, and M wB, for the x  lx 
 mV cm
bare hull plus horizontal tail configuration. This is 1−−  − 
 l Sl  l l 
presented below. The prime notation above indicates CC= tb (8) 
 mm
 α x V
a dimensionless coefficient, and Peterson accepted q,B ,B 1−−m
 l Sl
the convention that all derivatives are non- tb
dimensional with respect to the body cross-sectional 
area Sb and the body length l S
 MC' = − b (9) 
 ' q,B 2 m
 Calculation of ZwB, : Peterson’s expression [2] l q,β
for Zw for the body alone is: 
 where lc is the distance from the nose to the entre of 
 S  buoyancy and Stb is the cross sectional area of the 
 ' =−+b
 Z CC (3) truncated base. The tail-alone lift-curve slope is 
 w,B 2 LD
 l α,B 0 calculated using the following [2]: 
where C is the body alone lift-curve slope and 
 Lα,B 2π AR S
 C = t (10) 
 C is the drag coefficient at zero lift. Given by CFD L 2 2 S
 D0 α ,T 2++ 4( AR) 1 + tan λ b
 ( c /2)
simulation. 
 ' where AR is the aspect ratio of the tail, λc/2 is the 
 Calculation of M w,B : The pitching moment/ sweep angle at the half-chord line, and St is the total 
angle of attack is calculated in DATCOM by tail planform area. The expression for the combined 
applying a viscous correction to the Munk moment body/tail lift-curve slope is then 
[2] 
 2π AR
 =
 CL 
 2 kk− l α ,wing 22 22
 ( ) v dS 2++ 4 4πλ( AR) ( 1 + tanc/2) /C α
 C = 21∫ (x− x) dx (4) L
 m S l dx m
 αβ, 0
 b (11) 
where xm is defined as being the distance from the For C is actually an approximate expression 
 Lα ,T
nose to the moment reference center and lv is the axial 
location of separation. The final expression for the which has been derived using thin wing theory, 
pitching moment is then: CLα= 2πα. The interference of the fuselage with the 
 wing [8], as well as the contribution of the fuselage 
 S itself to the lift, is taken into account using the 
 MC' =b (5) 
 w,B 2 m following expression: 
 l α,β
 C= KC (12) 
 L wf L
 ' αα,w f , wing
 Calculation of Zq,B : Peterson considers only 
the contribution of the bare hull to Zq and Mq [2]. where Kwf is a correction factor which has the form: 
 x 2
 m dd
 CC=1 − (6) ff
 LLl K =+−1 0.025 0.25 (13) 
 q,Bα ,B  wf bb
 
where xm is the distance from the nose to the moment 
 where d is the maximum fuselage diameter and b is 
reference center. Zq is then given by f
 the wing span [6], [7]. 
 45 
 Journal of Science & Technology 146 (2020) 043-048 
 C
 Lα AR = ∞
 = (14) 
 C α
 L C
 Lα AR = ∞
 1+
 π AR
 C2
 CC= + L (15) 
 DD
 0 π AR
where AR is the aspect ratio, C is the wing lift 
 L Fig. 3. Velocity contour around AUV 
coefficient 
 5. Results and Discussions 
4. The AUV Model 
 First, the drag and lift coefficients of AUV 
 To identify hydrodynamic coefficients of the motion have been calculated by using CFD method. 
AUV, a model of AUV is used in this study. The The steady state CFD was successfully applied to 
principal parameters of AUV are shown in Table 2. simulate the straight line. Reynolds-averaged Navier-
Table 2. Principal technical parameters of AUV Stokes (RANS) equations are time-averaged 
 equations of motion for fluid flow and as an approach 
 Symbol 
 Content Value to solve Navier-Stokes equations [5]. Fig. 3 shows the 
 (Unit) velocity contour around AUV and for calculation of 
 Length L(mm) 3013 the necessary values as CL, CD, CM when using the 
 Height H(mm) 462 tools above. 
 Diameter D(mm), df 300 The AUV has been carried simulation with its 
 Draught without water T(mm) velocity from 0.5 m/s to 5.0 m/s and the vehicle 
 296 
 in the 4 floats moves in infinite fluid with three different turbulent 
 models of k − ε . Fig.3 shows the velocity contour 
 Weight M(Kg) 200 
 around AUV for 3m/s. Table 3 and Fig.5 show the 
 Wingspan b(mm) 462 drag and drag coefficient of the AUV whit diferent 
 Sea water density ρ(kg/m3) 1035 velocities. The drag coefficient of AUV is identified 
 Velocity V(m/s) 2.0 by using equation (16) below. 
 2
 Moments of inertia Ixx(kgm ) 2.2184 2 F
 C = D (16) 
 Centre of gravity G(x,y,z) 0, 0, 0 D ρ SV2
 Centre of buoyancy B(xb,yb,zb) 0, 0, 50 
 3
 FD(N) - Force resistance (drag); ρ = 1035kg/m - 
 density of sea water, S = 0.07065m2 - reference area 
 (the cross perpendicular section with motion). 
 Fig. 2. Geometry of underwater vehicle Fig. 4. Velocity contour around the aft of AUV 
 46 
 Journal of Science & Technology 146 (2020) 043-048 
Table 3. Drag/Drag coefficient in the function of The hydrodynamic stability derivatives are 
velocity determined through DATCOM method, combined 
 with CFD simulation. For the longitudinal 
 Velocity (m/s) Drag FD (N) Drag coefficient 
 coefficients note that Xu, Zw, Zq, Mw, and Mq were 
 CD 
 important coefficients, while Zu and Mu were less 
 0.5 2.22 0.24 significant. These other longitudinal coefficients are 
 1.0 8.77 0.24 zero [8]. Table 5 shows the calculated values for the 
 1.5 18.92 0.23 four longitudinal hydrodynamic coefficients for this 
 2.0 36.41 0.24 AUV. 
 2.5 53.92 0.23 
 3.0 82.14 0.25 Table 5. Longitudinal hydrodynamic coefficients 
 3.5 115.99 0.26 Coefficients Value Math 
 4.0 151.50 0.25 calculated (x10-3) formula 
 4.5 191.75 0.24 
 Z’W -1.79 (3) 
 5.0 236.73 0.25 
 M’W 0.882 (5) 
 Z’q -14.4 (7) 
 M’q -0.455 (9) 
 The data experimental for this AUV is not 
 available so in order to check the correctness of this 
 method, we use the test values obtained from 
 documentation [2]. 
 Table 6 shows the comparison of calculated and 
 experimental values for Torpedo 13 done by Hyguess 
 [2]. 
 Table 6. Comparison of calculated and experimental 
 values. 
 Fig. 5. Resistance of AUV 
 Coefficient Value Experiment Percentage 
 Fig. 4 shows the velocity around the aft body of calculated difference 
AUV when the AUV moves near the seabed and for 
 Z’W -0.593 -0.60 1.2 
calculation of tail lift curve slope. 
 M’W 0.993 0.99 0.0 
 Using the math formulas from equations (10) to Z’q -0.209 -0.20 5.0 
(15), the parameters of aft Hydroplanes are calculated 
in Table 4. M’q -0.074 -0.08 7.5 
 Method CFD for the calculation of the lift and Table 6 shows that the percentage difference 
drag coefficient of alone wing are clearly presented in between values calculated and experimental is 
(6) and do not need to be repeated here. acceptable. From there the results calculated in table 
 5 can be accepted. 
Table 4. Designed and calculated parameters of Aft 
Hydroplanes NACA 0012 6. Conclusion 
 Parameter Values Remark A detailed description of the calculation of each 
 of four longitudinal hydrodynamic coefficients of 
 Aspect ratio of the tail 3.7 AR AUV is identified by DATCOM method, based on 
 Sweep angle at the half- 20o λc/2 techniques developed in the aeronautical industry. In 
 chord line this paper, DATCOM method is used to calculate the 
 Total 0.0579m2 St hydrodynamic coefficients for an AUV with a 
 tail planform area torpedo shape. 
 -1
 Tail-alone lift-curve slope 5.63 rad CLα The calculated values have been compared with 
 -1
 Tail-alone lift-curve slope 3.49 rad CLα,t experimental results of a torpedo shape. It was 
 -1
 Tail-fuselage lift-curve 3.79 rad CLα,tf concluded that the methods described above could 
 slope calculate accurate values of the hydrodynamic 
 coefficients for a specific AUV shape with its 
 Drag coefficient of tail 0.0213 CDt 
 47 
 Journal of Science & Technology 146 (2020) 043-048 
elliptical nose, the main body is cylindrical and the Dynamics Laboratory, Wright Patterson Air Force 
aft is conical. Base, April, 1976 
Acknowledgments [4] Fossen T. I., Handbook of Marine Craft 
 Hydrodynamics and Motion Control, Wiley, 2011. 
 This work is supported by the Ministry of 
 [5] Lê Quang, Pham T.T. Hương, Tính toán các đặc tính 
Science and Technology with project code: 
 động lực học và khảo sát ổn định chế độ hạ cánh của 
NĐT.68.RU/19. máy bay phản lực luyện tập loại nhỏ, Báo Tạp chí Cơ 
References khí, Số 6(2019). 68-72 
[1] Martin Renilson, Submarine Hydrodynamics, [6] Robert C. Nelson. Flight Stability and Automatic 
 Springer, ISBN 978-3-319-16184-6, 2015 Control. 2 rd Edition, McGraw-Hill, 1984. 
[2] D.A. Jone, D.B. Clarke, I.B. Brayshaw, J.L. Barillon, [7] M. Nita, D. Scholz. Estimating the Oswald Factor 
 B. Anderson, The Calculation of Hydrodynamic from Basic Aircraft Geometrical Parameters, 
 Coefficients for Underwater Vehicles, Victoria, Deutscher Luft-und Raumfahrtkongress (2012). 14-19 
 DSTO COA, Australia, 2002 [8] Vepa Ranjan. Flight Dynamics, Simulation and 
[3] Finck, R.D. “USAF Stability and Control Data Control for Rigid and Flexible Aircraft. CRC Press, 
 Compendium” (DATCOM), Air Force Flight Taylor & Francis Group, LLC, 2015 
 48