Giáo trình Vật lý đại cương - Chương 3: Động lực học hệ chất điểm. Vật rắn
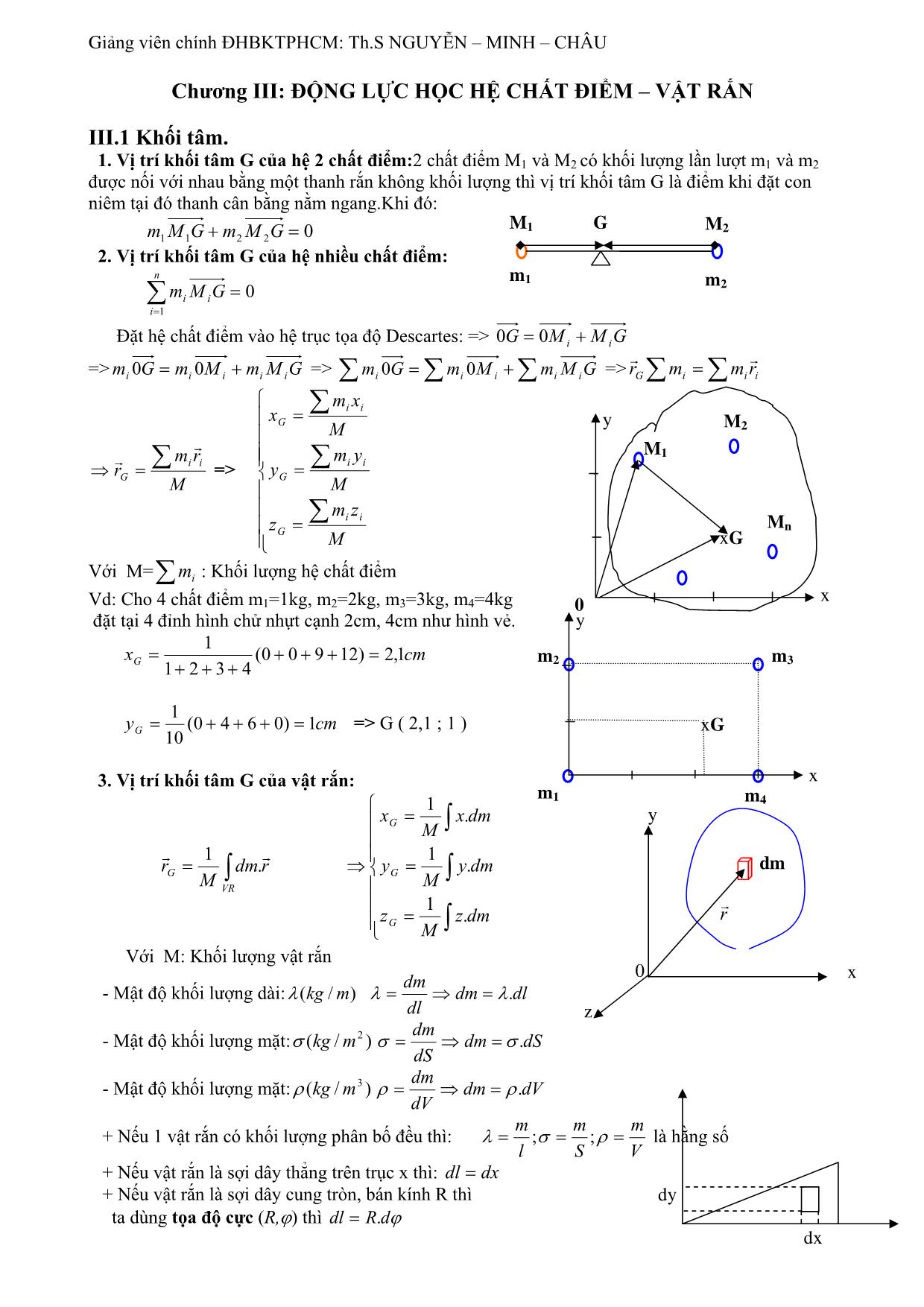
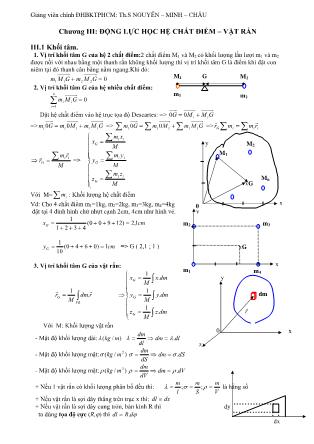
Vị trí khối tâm G của hệ 2 chất điểm:2 chất điểm M1 và M2 có khối lượng lần lượt m1 và m2
được nối với nhau bằng một thanh rắn không khối lượng thì vị trí khối tâm G là điểm khi đặt con
niêm tại đó thanh cân bằng nằm ngang.
Vd: Cho 4 chất điểm m1=1kg, m2=2kg, m3=3kg, m4=4kg
đặt tại 4 đỉnh hình chử nhựt cạnh 2cm, 4cm như hình vẻ.
+ Nếu vật rắn là mặt phẳng giới hạn bởi 2 đường thẳng: = .dydxdS
+ Nếu vật rắn là mặt phẳng giới hạn bởi cung tròn: = . ddrrdS ϕ .
+ Nếu vật rắn là mặt cầu bán kính R thì: = 2 .sin ddRdS ϕ
Trang 1

Trang 2

Trang 3

Trang 4
Trang 5
Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Bạn đang xem tài liệu "Giáo trình Vật lý đại cương - Chương 3: Động lực học hệ chất điểm. Vật rắn", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Giáo trình Vật lý đại cương - Chương 3: Động lực học hệ chất điểm. Vật rắn
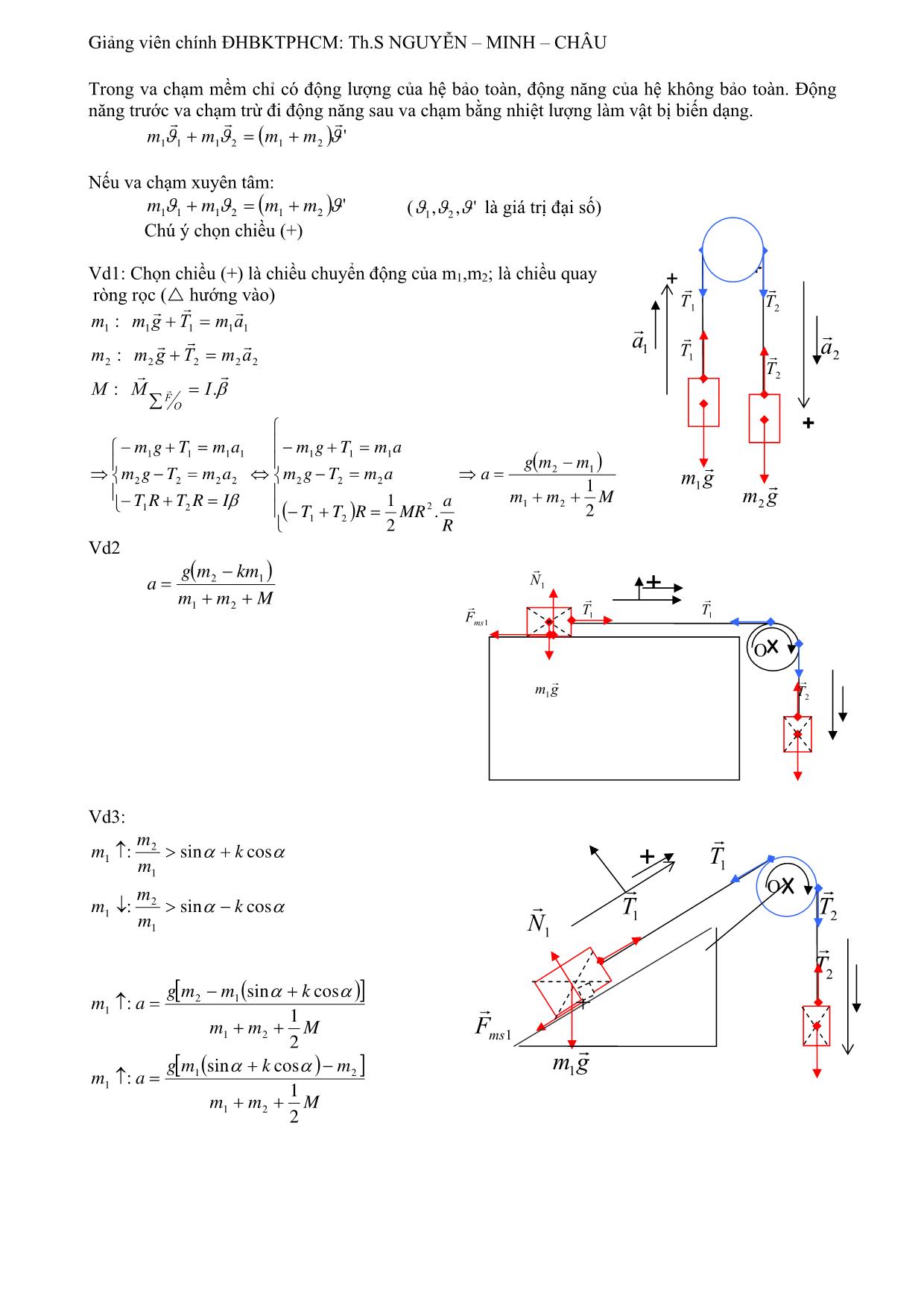
Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU Chương III: ĐỘNG LỰC HỌC HỆ CHẤT ĐIỂM – VẬT RẮN III.1 Khối tâm. 1. Vị trí khối tâm G của hệ 2 chất điểm:2 chất điểm M1 và M2 có khối lượng lần lượt m1 và m2 được nối với nhau bằng một thanh rắn không khối lượng thì vị trí khối tâm G là điểm khi đặt con niêm tại đó thanh cân bằng nằm ngang.Khi đó: M1 G M2 m1 M 1 G+ m2 M 2 G = 0 2. Vị trí khối tâm G của hệ nhiều chất điểm: n m1 m2 ∑ mi Mi G = 0 i=1 Đặt hệ chất điểm vào hệ trục tọa độ Descartes: => 0GMMG=0 i + i r r => mi 0 G= mi0 M i + m i M i G => ∑ mi 0 G= ∑ mi0 M i + ∑ mi M i G => rG∑ m i = ∑ mi r i ⎧ m x x = ∑ i i ⎪ G y M2 ⎪ M m r ⎪ m y M1 r ∑ i i ⎪ ∑ i i ⇒rG = => ⎨yG = M ⎪ M ⎪ ∑ mi z i ⎪zG = Mn ⎩⎪ M xG Với M= ∑mi : Khối lượng hệ chất điểm Vd: Cho 4 chất điểm m =1kg, m =2kg, m =3kg, m =4kg x 1 2 3 4 0 đặt tại 4 đỉnh hình chử nhựt cạnh 2cm, 4cm như hình vẻ. y 1 x = (0+ 0 + 9 + 12) = 2,1cm m m G 1+ 2 + 3 + 4 2 3 1 y =(0 + 4 + 6 + 0) = 1cm => G ( 2,1 ; 1 ) xG G 10 3. Vị trí khối tâm G của vật rắn: x m1 m ⎧ 1 4 x = x. dm y ⎪ G M ∫ ⎪ 1 ⎪ 1 r = dm. r ⇒ y = y. dm dm G ∫ ⎨ G ∫ M VR ⎪ M ⎪ 1 z = z. dm r ⎪ G ∫ ⎩ M Với M: Khối lượng vật rắn 0 dm x - Mật độ khối lượng dài: λ(/)kg m λ = ⇒dm = λ. dl dl z dm - Mật độ khối lượng mặt:σ (/kg m 2 ) σ = ⇒dm = σ. dS dS dm - Mật độ khối lượng mặt: ρ(/kg m3 ) ρ = ⇒dm = ρ. dV dV m m m + Nếu 1 vật rắn có khối lượng phân bố đều thì: λ=;; σ = ρ = là hằng số l S V + Nếu vật rắn là sợi dây thẳng trên trục x thì: dl= dx + Nếu vật rắn là sợi dây cung tròn, bán kính R thì dy ta dùng tọa độ cực (R,ϕ) thì dl= R. dϕ dx Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU r= x2 + y 2 x= r cosϕ Tọa độ cực: y ⎧ ϕ = arctg Với ⎨ x ⎩y= r sinϕ r dϕ d + Nếu vật rắn là mặt phẳng giới hạn bởi 2 đường thẳng: dS= dx. dy ϕ + Nếu vật rắn là mặt phẳng giới hạn bởi cung tròn: dS= r.. dr dϕ . z + Nếu vật rắn là mặt cầu bán kính R thì: dS= R2 sinθ . d θ . d ϕ ⎧x= r sinθ cos ϕ ⎪ Tọa độ cầu: M (,,)r θ ϕ với ⎨y= r sinθ sin ϕ M ⎪z= r cosθ ⎩ θ π 2π r 2 Khi tính biết mặt cầu: S= R∫sinθ . d θ ∫ d ϕ y 0 0 + Nếu vật rắn dạng khối lăng trụ hay lập phương: dV= dx.. dy dz ϕ + Nếu vật rắn là khối cầu: dV= r2 dr.sinθ . d θ . d ϕ x R R ππ2 R 3 4 V= ∫ r2 dr ∫sin V= ∫ r2 . dr∫∫ sinθ . d θ d ϕ = .2.2π= πR 3 0 0 0 0 0 3 3 Vd1: Cho vật tam giác vuông OBC ( OB=a và BC=b) khối lượng m phân bố đều. Tìm G? m y b y= x 1 a a 1 ab a 2 C x = σ..dx dy = 2 xdx.. dy = x.. dx y G ∫ ∫∫ ∫ m VR m 00ab 0 1 d y • Tương tự y= b : G 3 0 B x dx Vd2: Cho vật rắn khối lượng m là ¼ vòng tròn (O,R). Xác định G? 1 y xG = σ.r . dr . d ϕ . r cos ϕ M ∫ 123 123 VR dS x M 2 π π R R 2 = 4 r2 drcosϕ . d ϕ M ∫∫ y G 0 0 3 π 4 R 2 4 = 2 . sinϕ 0 =RR ≡ 0,424 x πR 3 3π x H hđối nxứng => xG = ì yG = 0,424R. r F ∑ i III.2. Chuyển động khối tâm G r 1 r rG = ∑ mi r i r M aG r G r drG 1 r 1 r ϑG = = ∑miϑ i = ∑ pi r dt M M ϑ r G dϑ 1 1 r ar =G = m ar = F G ∑i i ∑ i r dt M M P ∑ i Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU III.3. Động lựơng của hệ chất điểm và vật rắn. r r rr a/ Định nghĩa: Pp==∑∑iiimMϑ =ϑG r r dP d(.) M ϑ r b/ Định lý: = G =Mar = F dt dt G ∑ c/ Định luật bảo toàn động lượng: r r - Bảo toàn toàn phương: ∑ F=0 ⇔ P = hs r - Bảo toàn 1 phương: ∑ F ≠ 0,∑ Fx = 0 ⇒ Px = hs r r r r Vd1: N r F= m gr + N + m gr + N = 0 1 r r N2 ∑ 1 1 2 2 m1 ϑ m2 r ϑ1 2 r r N1 PPTVC = SVC r r r r m...'.'ϑ+ m ϑ = m ϑ + m ϑ m gr m gr 1 1 2 2 1 1 2 2 1 2 Vd2: m r r PPTB = SB M r r r r V ()'m+ M V = mϑ + MV ' Vd3: r ϑ r r PP1= 2 r r r V 0 = mϑ + MV Vd4: Bảo toàn 1 phương: r ϑ' r F= mgr ⇒ F = 0 r ∑ ∑ X ϑ r r r ()'m+ M V ≠ mϑ + MV ' r V' P = P X TVC X SVC M => mϑ = MV' V=0 III.4. Vật rắn chuyển động tịnh tiến. 1/ Định nghĩa: Khi vật rắn chuyển động tịnh tiến thì mọi chất điểm của vật rắn chuyển động cùng quãng đường, cùng vận tốc và cùng gia tốc với khối tâm. A1 A2 B 1 B 2 AABBGG1 2= 1 2 =... = 1 2 G G ϑAB= ϑ =... = ϑG C1 C2 aAB= a =... = aG 2/ Động năng của vật rắn chuyển động tịnh tiến: 1 2 1 2 Wđ =Wđ = ..m ϑ= M . ϑ tt ∑i ∑ 2 i i 2 G 3/ Phương trình động lực học của vật rắn chuyển động tịnh tiến: r r ∑ Fi = M. aG III.5. Vật rắn chuyển động quay quanh 1 trục U. Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU Δ 1/ Định nghĩa: θ AB=θ =... = θ v ω AB=ω =... = ω A1 β AB=β =... = β Khi vật rắn quay quanh 1 trục thì mọi chất điểm có cùng 1 θA góc quay, cùng vận tốc góc và cùng gia tốc góc. A2 2/ Động năng của vật rắn quay quanh 1 trục U: 1 2 1 2 2 1 2 2 Wđ q / Δ =∑Wđ i = ∑mi.ϑ i = ∑ mi..ω i r i = ω .∑ mi r i 2 2 2 B2 Với ri : khoảng cách từ chất điểm thứ i đến trục U. θB 2 Đặt IΔ = ∑ mi r i : moment quán tính của hệ chất điểm đối với trục U B1 1 => WIđ = .ω 2 q / Δ 2 Δ 3/ Moment quán tính của hệ chất điểm đối với trục quayU: 2 IΔ = ∑ mi r i 4/ Moment quán tính của vật rắn đối với trục quayU: I= dm. r 2 Δ ∫ VR Vd1: Cho 1 thanh thẳng khối lượng M, dài L, khối lượng phân bố đều. Tính moment đối với trục quayU vuông góc với thanh và đi qua điểm giữa. L L Δ Δ 2 M x 3 2 I = λ dx x 2 = Δ Δ ∫ ... L L 3 L − − 2 2 r 3 3 2 M ⎛ L⎛ L⎞⎞ ML =⎜ −⎜ − ⎟⎟ = α dx ⎜ ⎜ ⎟⎟ x L ⎝ 24⎝ 24⎠⎠ 12 O O x d Δ + Nếu chọn gốc O đối với trục U’: L M x 3 1 I =. = ML2 Δ' L 3 0 3 + Nếu chọn trục U2 lệch góc α với thanh: M L M L3 ML2 I = dx. x 2 sin 2 α = sin2 α . = sin2 α Δ 2 ∫ L 0 L 3 3 + Nếu chọn trục U3 song song với thanh: I =dm. d2 = d 2 dm = M. d 2 Δ 3 ∫ ∫ VR Δ Vd2: Cho 1 vành khối lượng M, bán kính R, U vuông góc vành qua O d I =dm. R2 = R 2 dm = M. R 2 Δ ∫ ∫ O R VR Vd3: Đĩa đặc phân bố đều Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU Δ I = σ....r dr d ϕ r 2 Δ ∫ M R 2π = r3 . dr dϕ dr 2 ∫ ∫ r πR 0 0 4 R 2 M r 2π MR. = . .ϕ = 2 0 πR 4 0 2 R2 2π Δ M 3 Vd4: Đĩa rổng bán kính R1,R2 I = r. dr dϕ Δ π ()RR2 − 2 ∫ ∫ 2 1 R1 0 4 4 M ⎡ RR2 1 ⎤ = 2 2 ⎢ − ⎥.2π R2 π ()RR2 − 1 ⎣ 4 4 ⎦ O R1 M =(RR2 + 2 ) 2 2 1 1 2 2 2 - Thanh dài: I= ML - Cầu đặc: I= MR Δ 12 Δ 5 2 - Vành, trụ rỗng: IΔ = MR 1 2 - Đĩa đặc, trụ đặc: I= MR Δ 2 2 2 - Cầu rỗng: I= MR Δ 3 3.5 Định lý Steiner-Huyghen: Trục U đi qua G Trục U’//U và cách U 1 đoạn d 2 IΔΔ' = I + Md Vd: Thanh rắn: Δ’ Δ 1 L 2 1 Δ 2 ⎛ ⎞ 2 IΔ' = ML + M ⎜ ⎟ = ML 12 ⎝ 2 ⎠ 3 R 2 2 2 I= MR + MR = 2 MR L/2 Δ' Lưu y: Moment quán tính có mang tính chất cộng I I I ()m+ M = m + M Δ' Δ Δ Vd: Hệ 1 niềng M, 6 căm M: III= + 6 Δ M / Δ m / Δ ⎛ 1 ⎞ =MR 2 + 6⎜ mR2 ⎟ =() M + 2 m R 2 ⎝3 ⎠ Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU + Nếu khoét đi 1 lỗ sẽ trừ đi:( M:k/l đĩa chưa khoét; M’:k/l đĩa đã khoét; m: k/l lổ khoét) III=− dk/ΔΔΔ 012 / 0 / M σ. πR 2 1322 = ⇒M = 4 m • O2 I =−MR mr 2 O1 dk/Δ m σ.. π r 22 1 ⎡ ⎛ R ⎞⎤ 1 13 2 xG =⎢0 +⎜ − m ⎟⎥ = − IMRdk/Δ = '. 3m ⎣ ⎝ 2 ⎠⎦ 6 24 Moment quán tính là giá trị vô hướng dương, (là giá trị số học) r III.6 Moment lực. M Δ r 1. Moment lực F đối với điểm O r r r r F r r r M F / 0 =r × F ⎧ -Điểm đặt: tại 0. uur ⎪ r r O r ⎪ -Phương: đt ⊥với mp tạo bởi ( r,) F . M F /0 ⎨ r r -Chiều: r, F, M tạo thành tam diện thuận. ⎪ uur r M F / Δ ⎩⎪ -Độ lớn: M= r. F sinα r r Δ Fz 2. Moment lực F đối với trục U r F r r r r MF / Δ = hcM F 0/ Δ r r 3. Moment lực F của vật rắn đối với trục U r r i r Tác dụng lên vật rắn 1 lực F để vật rắn quay quanh U. F r t Lực F được phân thành 3 thành phần: r r r r r M r F' FFFF=t + n + z Fn r r r Fz : làm vật trượt trên U, không làm vật rắn quay => M Fz / Δ = 0 r r M r 0 Fn : kéo vật trượt trên U, không làm vật rắn quay => Fn / Δ = r r r r Mr r Ft Ft : làm vật rắn quay quanh U => tF / Δ = × ( r: khoảng cách từ M đến U ) r ⎧F = 0 r ⎪ r M r =0 ⇔ F Δ ≠ φ F / Δ ⎨ I ⎪ r ⎩⎪F // Δ 3.6.4 Moment tổng ngọai lực của vật rắn đối với U: uur r rrr r MrΣΔF / =×=×Frma. ∑∑iiti iit uur r rrrr rrrrr M ΣΔF / =××=mr⎡⎤⎡(ββ r ) m (.). rr − (. rβ ). r ⎤ ∑∑ii⎣⎦⎣ i i i iii iii ⎦ uur r 2 rr MmrIΣΔF / ==∑ ii..ββΔ . Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU 3.6.5 Phương trình động lực học cơ bản của vật rắn quay quanh U: uur r r M ΣΔF / = I Δ .β r III.7. Moment động lượng. L r 3.7.1 Moment động lượng L đối với O r r L= r × P ( r : vectơ vị trí) i /O i i i Điểm đặt: tại O ⎧ r ⎪ Phương: vuông góc mặt phẳng tạo bởi (r, P ) ⎪ i i ⎨ r r r Chiều: ri,, P i L/ O tạo thành U diện thuận ⎪ r ⎪ ⎩ Độ lớn: LrpiO/ = i..ni i α s 3.7.2 Moment động lượng đối với U: r r L/ Δ = hình chiếu L/ O Δ 3.7.3 Moment động lượng của vật rắn đối với U: r r r r r r L Δ = L i =ri × p i = ri × m iϑ i ∑ Δ ∑ ∑ r r r r r r r r r = ∑ mi[ r i × (ω i ×r i )] = ∑ mi[( r i . r i )ω i− ( r i . ω i ). r i ] 2 r r = ∑ mi.. r iω i = I Δ ω uur r r Ghi chú: M ΣΔF / của vật rắn đối với trục U thì cùng phương, chiều với β r r L/ Δ của vật rắn đối với trục U thì cùng phương, chiều với ω 3.7.4 Định lý moment động lượng: r dL dωr r / Δ =I .. =I β = dt / Δ dt / Δ 3.7.5 Định luật bảo tòan moment động lượng: r 2 1 t ìL/ Δ = const h Vd: Ghế Giucopxki (người đi từ mép đĩa đến R/2) r r LLIIII= ⇒()() +ω = + ' ω ΔΔ1 2 1 2 1 1 2 2 M 2 ⎛ 1 2 2 ⎞ ⎛ 1 2 R ⎞ ⇒ ⎜ MR+ mR ⎟ω1 =⎜ MR + m ⎟ω2 G 2 ⎜ 2 4 ⎟ ⎝ ⎠ ⎝ ⎠ Vd: Viên đạn chạm thanh M, L: r r M ∑ F Δ =0 ⇔LΔ = hs r r r m ϑ LLTVC = SVC 1 ϑ 1 ML2 .0+ mL2 . =ML2 .'.' Ω + mL2 ω 3 L 3 III.8. Vật rắn chuyển động lăn không trượt. Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU 3.8.1 Định nghĩa1: khi vật rắn lot là vừa chuyển động tịnh tiến theo khối tâm G và vùa chuyển động quay quanh G r r ⎧ϑ ⎧ω Tịnh tiến G Quay quanh G ⎨r ⎨ r ⎩aG ⎩β A AB= G1G 2 = cungAB= Rθ θ dθ G G ϑG =R = ωR dt ⇒ a= β R A B G r • Vectơ vận tốc của chuyển động lot tại G, A, B, C ϑ r r r r A Att - Xét chuyển động tịnh tiến: ϑGABC= ϑ = ϑ = ϑ r r ϑ ϑ Alot - Xét chuyển động quay quanh G: Aq r ϑGtt=ϑAq=ϑBq=ϑCq . ϑGq=0 ϑ r Gtt ϑ G B Btt - Xét chuyển động lot: r r ϑGq ϑGlot r r r ϑ= ϑ + ϑ r lot ttG qG r ϑ Blot C ϑ Bq rrrrrrr r r r Vậy: ϑϑϑϑϑAlot===2; Gtt Glot Gtt ; Blot . ϑϑ ;2Gtt Clot ;= 0=ϑICq β ϑClot ϑCtt ϑ Định nghĩa 2: Lot là quay quanh tâm quay tức thời ()ϑ=0 : ω = G lot R 3.8.2 Động năng của vật rắn Lot: 1 1 WWWMI= + =ϑ2 + ω 2 ñ/ lot ñttG ñqG 2 G 2 G 3.8.3 Phương trình cơ bản ĐLH của Lot: r r ∑ Fi = M. aG uur r r M ΣΔF / = I .β • Chú ý; Δ ur *Trong cđ Lot có lực ma sát lăn: là dạng lực ma sát tỉnh: F msl - Điểm đặt: điểm tiếp xúc. - Phương: phương chuyển động tịnh tiến. ur ur - Chiều: * F đi qua G: F msl ngược chiều tịnh tiến ur ur * F 0 đi qua G: F msl cùng chiều tịnh tiến - Độ lớn:Phải tìm và 0 ≤ Fmsl ≤ kN. * Công của lực ma sát lăn bằng không (dl=0). r aG ar G + r r r + ⎧Mgr + N + F + F = Mar r r ⎪ msl G r F N ⎨ r r N MIr = β ⎪ F G r ⎩ ∑ G F G G r r F F msl msl Hình 1 r Mgr Hình 2 Mg Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU ⎧+F + F = Ma ⎧−F + F = Ma msl G msl G ⎪ ⎪ ⎨ ⎛ 1 2 ⎞⎛ aG ⎞ ⎨ ⎛ 1 ⎞⎛ a ⎞ ⎪−Fmsl .. R + F R = ⎜ MR ⎟⎜ ⎟ 2 G ⎝ 2 ⎠ R ⎪+FRImsl .. =G β = ⎜ MR ⎟⎜ ⎟ ⎩ ⎝ ⎠ ⎩ ⎝ 2 ⎠⎝ R ⎠ 2 F F 4 F F aG = Fmsl = aG = Fmsl = 3 M 3 3 M 3 r r ⎧−F + Mg sinα = Ma (1) ⎧Mgr + N + F = Mar msl G ⎪ msl G ⎪ ar ⎨ r r ⎨ 2 ⎛ aG ⎞ G MIr = G β +F.. R = Iβ = MR ⎜ ⎟ (2) r ⎪ F ⎪ msl G () N ⎩ ∑ G ⎝ R ⎠ r ⎩ + F G msl Vành: a =1/2 gsinα F = Ma G ms G Đĩa: aG=2/3 gsinα Fms= 1/2MaG Cầu rổng: aG=3/5 gsinα Fms= 2/3MaG α Mgr Cầu đặc: aG=5/7 gsinα Fms= 2/5MaG Tròn trượt o ms: aG= gsinα III.9.Va chạm. 3.9.1 Va chạm đàn hồi: r r TVC m1ϑ 1, m 2 ϑ 2 r ' r ' SVC m1ϑ 1 , m2 ϑ 2 Trong va chạm hòan tòan đàn hồi thì động lượng của hệ và động năng hệ bảo tòan; r r r r r r ⎧P= P → mϑ + m ϑ = m ϑ' + m ϑ ' ⎪ TVC SVC 1 1 2 2 1 1 2 2 ⎨ r r 1 2 1 2 1 '2 1 '2 ⎪WñTVC = WñSVC = m1ϑ 1 + m2 ϑ 2 = m1 ϑ 1 + m2 ϑ 2 (1) ⎩ 2 2 2 2 • Nếu va chạm xuyên tâm: ' ' ' ' m1ϑ 1+ m 2 ϑ 2 = m 1 ϑ 1 + m2 ϑ 2 (2) (ϑ1,,, ϑ 2 ϑ 1 ϑ2 là giá trị đại số) r r ' m− m 2m m2 1 2 2 m1 ϑ1 ϑ 2 (1), (2) ⇒ϑ1 = ϑ1 + ϑ2 m1+ m 2 m1+ m 2 G G2 1 + ' 2m1 m2− m 1 ⇒ϑ2 = ϑ1 + ϑ2 m1+ m 2 m1+ m 2 : d V r r •LLTVC = SVC 1 ϑ 1 ϑ ' ⇔ ML2ω + ml2 . = ML2ω '+ ml 2 . L 3 l 3 l •WWñTVC = ñSVC l G 1 ⎛ 1 ⎞ 1 ϑ 1 ⎛ 1 ⎞ 1 ϑ 2 ⇔ ⎜ ML2⎟ω 2 +ml2 . = ⎜ ML2⎟ω '2 + ml2 . 2 ⎝ 3 ⎠ 2 l 2 ⎝ 3 ⎠ 2 l 2 1 ⎛ 1 ⎞ 1 ϑ 2 1 ⎛ 1 ⎞ 1 ϑ'2 ⎜ ML2 ⎟×0 +()ml 2 × = ⎜ ML2 ⎟× Ω'2 +()ml 2 × (2) 2 ⎝ 3 ⎠ 2 l 2 2 ⎝ 3 ⎠ 2 l 2 3.9.2 Va chạm mềm: r r ⎧TVC m1ϑ 1, m 2 ϑ 2 ⎨ r ⎩SVC ()m1+ m 2 ϑ' Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH – CHÂU Trong va chạm mềm chỉ có động lượng của hệ bảo toàn, động năng của hệ không bảo toàn. Động năng trước va chạm trừ đi động năng sau va chạm bằng nhiệt lượng làm vật bị biến dạng. r r r m1ϑ 1+ m 1 ϑ 2 =() m 1 + m 2 ϑ' Nếu va chạm xuyên tâm: m1ϑ 1+ m 1ϑ 2 =() m 1 + m 2 ϑ' (ϑ1,,'ϑ 2 ϑ là giá trị đại số) Chú ý chọn chiều (+) O + Vd1: Chọn chiều (+) là chiều chuyển động của m1,m2; là chiều quay + r r ròng rọc (U hướng vào) T T r r r 1 2 m1: m 1 g+ T 1 = m 1 a 1 r r r r r r a1 T a m2: m 2 g+ T 2 = m 2 a 2 1 r 2 T r r 2 r MMI: F = .β ∑ O ⎧ + ⎧−m g + T = m a ⎪−m g + T = m a 1 1 1 1 ⎪ 1 1 1 g m− m ⎪ ()2 1 r ⇒ ⎨m2 g− T 2 = m 2 a 2 ⇔ ⎨m2 g− T 2 = m 2 a ⇒a = m g ⎪ ⎪ 1 1 r −TRTRI + = β 1 a m1+ m 2 + M m g ⎩ 1 2 ⎪()−T + T R = MR 2 . 2 2 ⎩ 1 2 2 R Vd2 r g() m2− km 1 N a = 1 + m+ m + M r r 1 2 r T T F 1 1 ms1 O m gr r 1 T2 Vd3: m m ↑:2 > sinα + k cos α r 1 m + T1 1 m r O r m ↓:2 > sinα − k cos α T T 1 m r 1 2 1 N1 r T2 g[] m− m()sinα + k cos α m↑: a = 2 1 1 1 r m1+ m 2 + M Fms1 2 r g[] m()sinα+ k cos α − m m g m↑: a = 1 2 1 1 1 m+ m + M 1 2 2
File đính kèm:
 giao_trinh_vat_ly_dai_cuong_chuong_3_dong_luc_hoc_he_chat_di.pdf
giao_trinh_vat_ly_dai_cuong_chuong_3_dong_luc_hoc_he_chat_di.pdf

