Giáo trình Vật lý đại cương - Chương 1: Động học chất điểm
.1 Các khái niệm cơ bản:
- Chất điểm là 1 vật có khối lượng, có kích thước rất nhỏ so với khoảng cách và kích
thước của vật khác.
- Hệ chất điểm: là tập hợp nhiều chất điểm rời rạc.
- Vật rắn: là tập hợp nhiều chất điểm phân bố liên tục và có mối liên kết rắn
(khoảng cách giữa các chất điểm là không thay đổi).
Vd: Đống cát không phải là vật rắn do khoảng cách thay đổi.
Cục gạch: vật rắn.
- Chuyển động: là sự thay đổi vị trí của chất điểm trong suốt quá trình chuyển động.
- Hệ quy chiếu: là hệ vật quy ước đứng yên để khảo sát các vật khác chuyển động
đối với nó. Thường người ta gắn hệ trục tọa độ vào hệ quy chiếu.
1.2 Phương trình chuyển động của chất điểm:
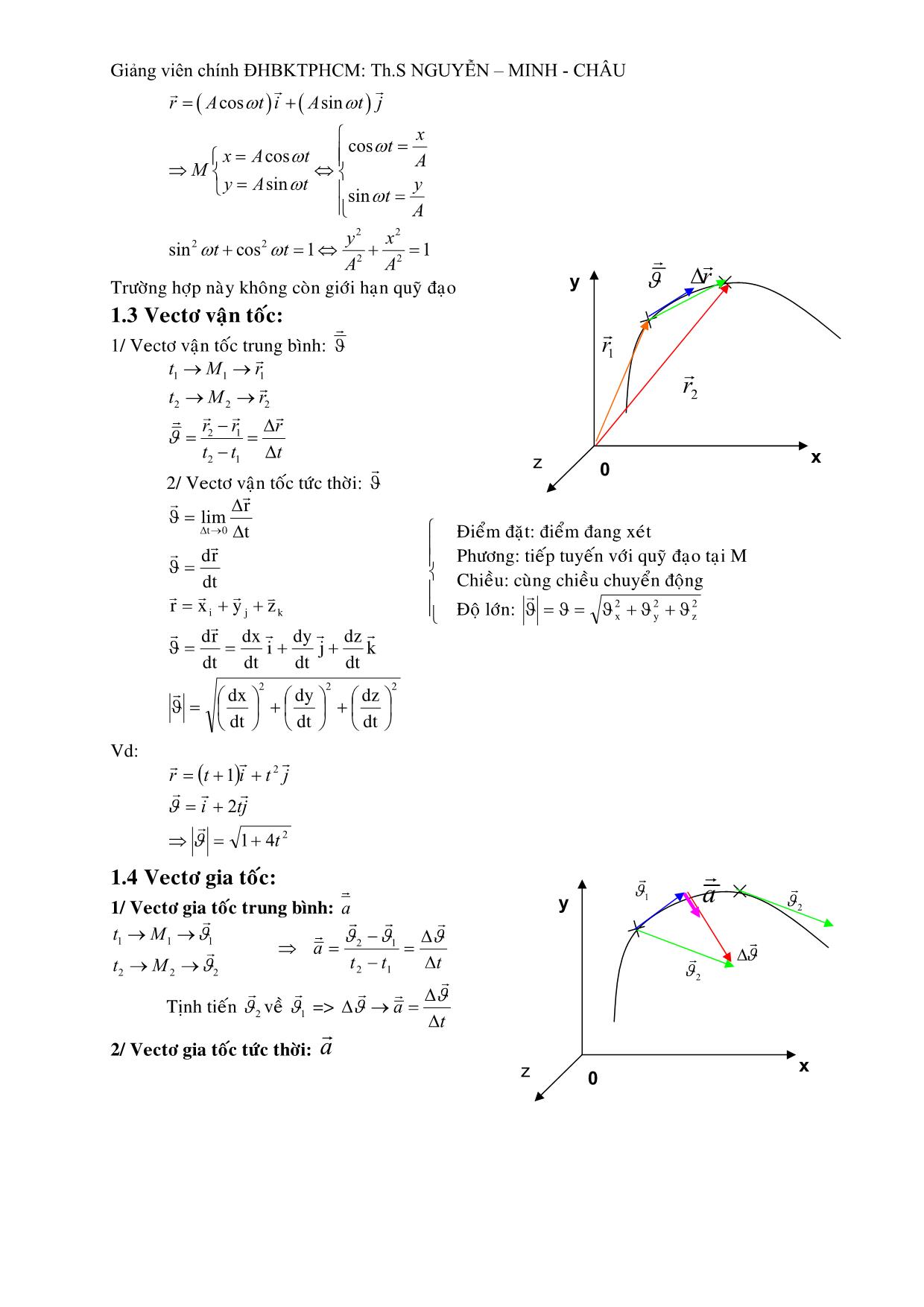
- Vectơ vị trí của chất điểm:
- Phương trình chuyển động của chất điểm M: .
*vectơ vị trí
* tọa độ điểm M
- Quỹ đạo của chất điểm M: f (x,y,z) = 0: là tập hợp
các vị trí của chất điểm trong suốt quá trình
chuyển động.
- Muốn tìm phương trình quỹ đạo của chất điểm, ta khử t ở phương trình chuyển
động chất điểm: 2 dạng
+ Dạng 1: phương pháp thế
+ Dạng 2: sin & cos theo t: áp dụng sin2 + cos2 = 1

Trang 1
Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
Tóm tắt nội dung tài liệu: Giáo trình Vật lý đại cương - Chương 1: Động học chất điểm

Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH - CHÂU Chương 1: ĐỘNG HỌC CHẤT ĐIỂM 1.1 Các khái niệm cơ bản: - Chất điểm là 1 vật có khối lượng, có kích thước rất nhỏ so với khoảng cách và kích thước của vật khác. - Hệ chất điểm: là tập hợp nhiều chất điểm rời rạc. - Vật rắn: là tập hợp nhiều chất điểm phân bố liên tục và có mối liên kết rắn (khoảng cách giữa các chất điểm là không thay đổi). Vd: Đống cát không phải là vật rắn do khoảng cách thay đổi. Cục gạch: vật rắn. - Chuyển động: là sự thay đổi vị trí của chất điểm trong suốt quá trình chuyển động. - Hệ quy chiếu: là hệ vật quy ước đứng yên để khảo sát các vật khác chuyển động đối với nó. Thường người ta gắn hệ trục tọa độ vào hệ quy chiếu. 1.2 Phương trình chuyển động của chất điểm: - Vectơ vị trí của chất điểm: rrr rxkjizyr =++... y x, y, z là hàm theo thời gian t. M ⎧x ⎪ Tọa độ điểm M: ⎨y ⎪ ⎩z r - Phương trình chuyển động của chất điểm M: . r j r *vectơ vị trí i * tọa độ điểm M r Z k 0 x - Quỹ đạo của chất điểm M: f (x,y,z) = 0: là tập hợp các vị trí của chất điểm trong suốt quá trình chuyển động. - Muốn tìm phương trình quỹ đạo của chất điểm, ta khử t ở phương trình chuyển động chất điểm: 2 dạng + Dạng 1: phương pháp thế + Dạng 2: sin & cos theo t: áp dụng sin2 + cos2 = 1 t r r Vd: r =i +() t2 − 2 j 2 ⎧ t ⎪x = ⎧t= 2x ≥ 0 M⎨ 2 ⇒ ⎨ 2 ⎪ 2 ⎩y=() 2x − 2 ⎩y= t − 2 ⇒y = 4x2 − 2 = 0 Giới hạn quỹ đạo: t > 0 → 2x > 0 → x > 0 Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH - CHÂU r r rAiAtjtr =+()()cosωω sin ⎧ x cosωt = ⎧xA= cosω t ⎪ A ⇒⇔M ⎨⎨ y = Atsinω y ⎩ ⎪sinωt = ⎩⎪ A yx22 sin22ωωtt+=+⇔ cos 1 =1 AA22 r r Trường hợp này không còn giới hạn quỹ đạo y ϑ Δr 1.3 Vectơ vận tốc: r r 1/ Vectơ vận tốc trung bình: ϑ r1 tMr→→r 111 r r r2 tMr222→→ r rr−Δ r ϑ ==21 tt21−Δ t x r z 0 2/ Vectơ vận tốc tức thời: ϑ r Δr ϑ = lim Δt → 0 Δt ⎧ Điểm đặt: điểm đang xét r ⎪ r dr ⎪ Phương: tiếp tuyến với quỹ đạo tại M ϑ = ⎨ Chiều: cùng chiều chuyển động dt ⎪ r r r v r 2 2 2 r= xi + y j + z k ⎪ ⎩ Độ lớn: ϑ = ϑ = ϑx + ϑy + ϑz r drr dx rdy rdz r ϑ = =i +j + k dt dt dt dt 2 2 2 r ⎛ dx ⎞ ⎛ dy ⎞ ⎛ dz ⎞ ϑ = ⎜ ⎟ + ⎜ ⎟ + ⎜ ⎟ ⎝ dt ⎠ ⎝ dt ⎠ ⎝ dt ⎠ Vd: r 2 r r=() t +1 i + t j r r r ϑ =i + 2 tj r ⇒ϑ =1 + 4t 2 1.4 Vectơ gia tốc: r ϑ r r r 1 a ϑ 1/ Vectơ gia tốc trung bình: a y 2 r r r r tM11→→ϑ1 r ϑ− ϑ Δϑ ⇒ a = 2 1 = r r t− tΔ t r Δϑ tM22→→ϑ2 2 1 ϑ r 2 r r r r Δϑ Tịnh tiến ϑ về ϑ => Δ→=ϑ a 2 1 Δt 2/ Vectơ gia tốc tức thời: ar x z 0 Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH - CHÂU r Δϑ ar = lim ⎧ Điểm đặt: điểm đang xét M Δ→t 0 Δt ⎪ Phương: đường thẳng đi qua M r dϑ ⎪ ar = ⎪ Chiều: hướng về bề lõm của quỹ đạo dt ⎪ Độ lớn: rrr aaiajakr =++... ⎨ r 2 2 2 xy z ⎪ a= a = ax + a y + a z r ⎪ dϑ dϑ dϑy dϑ r 2 2 2 r x rrz d aij== + +k ⎪ ⎛ dϑx ⎞ ⎛ ϑ y ⎞ ⎛ dϑz ⎞ dt dt dt dt ⎪ = ⎜ ⎟ + ⎜ ⎟ + ⎜ ⎟ ⎩ ⎝ dt ⎠ ⎝ dt ⎠ ⎝ dt ⎠ 222222 r ⎛⎞⎛⎞⎛⎞dx dy dz a =++⎜⎟⎜⎟⎜⎟222 ⎝⎠⎝⎠⎝⎠dt dt dt Vd: r r rrrrdϑ rr 22 ϑ =+itja2020 ⇒ = = i + ja ⇒ = +22 = dt Vectơ gia tốc tức thời được chiếu lên phương tiếp tuyến và pháp tuyến, ta có vectơ gia r r tốc tiếp tuyến at và vectơ gia tốc pháp tuyến an . r Vectơ gia tốc tiếp tuyến at Điểm đặt: điểm đang xét ⎧ r ⎪ Phương: tiếp tuyến với quỹ đạo tại M (cùng phương ϑ ) ⎪ r Chiều: dϑ > 0 , ϑ > ϑ : chuyển động nhanh dần => ar ↑↑ϑ ⎪ 2 1 t ⎨ r r ⎪ dϑ at ↑↓ ϑ ⎪ ⎪ ⎪ dϑ ⎩ Độ lớn: ar = a = t t dt M r Vectơ gia tốc tiếp tuyến at đặc trưng cho sự biến đổi về độ lớn của vectơ vận tốc. Chiều đặc trưng: chậm dần, nhanh dần. ⎧ Điểm đặt: điểm đang xét ⎪ ⎪ Phương: đt ⊥ tiếp tuyến với quỹ đạo tại M r ⎨ Chiều: hướng vào tâm của vòng tròn quỹ đạo tại M a ⎪ n 2 ⎩⎪ ϑ Độ lớn: an = (R: bán kính quỹ đạo tại M) R r r Do đó để tìm bán kính cong: phải có độ lớn ϑ và an . r Vectơ gia tốc pháp tuyến an đặc trưng cho sự thay đổi về phương của vectơ vận tốc. r an nhỏ => R lớn Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH - CHÂU r ϑ r ϑ r 1 an1 r ϑ2 r an2 r an lớn => R nhỏ Vectơ vận tốc tức thời: r r r a= at + a n r 2 2 a= at + a n ar đặc trưng cho sự thay đổi về độ lớn và phương của vectơ vận tốc. 1.5 Chuyển động thẳng: ϑ 2 Quỹ đạo là đường thẳng: →R = ∞ → a = 0 (vì a =; R = ∞ → a = 0 ) n n R n Nên đưa chuyển động thẳng về 1 trục -> chỉ cần 1 thành phần để biểu diễn. r rxixr =→. r r dx ϑϑ=→i ϑϑ~ = xxdt r dϑ dx2 aaiaar =→~ =x = xxdt dt 2 r uuuuur 1/ Chuyển động thẳng đều: ()ϑ = const dx x t ϑ = =const ⇒ dx =ϑ dt ⇔ dx =ϑ dt ⇔ x =ϑ t + x dt ∫ ∫ 0 x0 0 2/ Chuyển động thẳng thay đổi đều: (ar = const) rrr uuuuur aan =⇒0 = at = const dϑ ϑ t dx a = →dϑ = a dt ⇒ϑ = at + ϑ = ∫ ∫ 0 dt ϑ 0 dt 0 x t 1 ⇒dx =() at +ϑ dt ⇔ x − x = at2 +ϑ t ∫ ∫ 0 0 2 0 x0 0 Hay: 1 x= at2 +ϑ t + x 2 0 0 2 ϑ− ϑ0 =2a() x − x0 r ar cùng chiều ϑ → chuyển động nhanh dần đều r ar ngược chiều ϑ → chuyển động chậm dần đều Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH - CHÂU 1.6 Chuyển động tròn: quỹ đạo là đường tròn ⇒ R = const 1/ Vectơ vận tốc góc ωr : ⎧ Điểm đặt: ∀ điểm∈trục vòng tròn quỹ đạo (vectơ trục) ⎪ Phương: trục của vòng tròn quỹ đạo ⎪ r ⎨ Chiều: theo quy tắc vặn nút chai ωr ω ⎪ ⎛ S ⎞ ⎪ d r ⎜ ⎟ ϑ r ⎩⎪ r d ⎝ R ⎠ 1 dS ϑ at Độ lớn: ω= ω = = =. = r dt dt R dt R R r an r r r r r Liên hệ giữa ϑ,, ωr R : ϑω= r × R β r 2/ Vectơ gia tốc góc: β ⎧ Điểm đặt: ∀ điểm∈trục vòng tròn quỹ đạo (vectơ trục). ⎪ Phương: trục của vòng tròn quỹ đạo . r ⎪ Chiều: dω >→0 β cùng chiều ωr (chuyển động nhanh dần) ⎪ ⎪ r r r ⎨ dω <→0 β ngược chiều ω (chuyển động chậm dần) β ⎪ ⎪ ⎛ ϑ ⎞ d⎜ ⎟ ⎪ r dω ⎝ R ⎠ 1 dϑ at ⎪ Độ lớn: β= β = = =. = ⎩ dt dt R dt R r r r r r r r r Liên hệ giữa at ,,β R : at =×β R ( at cùng chiều ϑ : nhanh dần) aRt = β. ϑω222.R aR== =ω 2. n RR 22 4 2 aaaR=+=tn ω +β 3/ Chuyển động tròn đều: r ϑ = const⎪⎫ ⎬ ⇒an = const R= const ⎭⎪ ar=0 → a r = a r t n ωr = const dθ θ t ω = ⇒dθ = ω dt ⇒ θ = ω t + θ dt ∫ ∫ 0 θ0 0 4/ Chuyển động tròn thay đổi đều: Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH - CHÂU r β = const⎫ ⎬,.at =β R ⇒ at = const R= const⎭ dω ω t β = ⇒dω = β dt ⇒ ω = β t + ω dt ∫ ∫ 0 ω0 0 dθ θ t 1 Mà: ω = ⇒dθ =() β t + ω dt ⇒ θ = βt2 + ω t + θ dt ∫ ∫ 0 2 0 0 θ0 0 2 2 ω− ω0 =2 β( θ − θ 0 ) r 1.7 Chuyển động trong gia tốc g :(chuyển động parabol) r agrr==− gj(1) r dϑ r r ar =⇒=− dϑ gj. dt dt r ϑ t r r ⇔=−dgjdtϑ . ∫∫r ϑ0 0 r rrϑ r t rr ⇔=−⇒−=−ϑϑr gt.. j 00ϑgt j ϑ0 r r r Mà: ϑ0= () ϑ 0 cos αi + ( ϑ0 sin α ) j r rrdrr ⇒=ϑϑ()()00cos αigtj +−⎣⎦⎡⎤ + ϑsin α = (2) 142 43 14442 4 4 43 dt ϑx ϑy rtr r ⎡⎤rr ⇒=dr ⎣⎦()(ϑα00cos i +−+ gt ϑαsin ) j dt ∫∫ r 2 2 r 0 0 mà: ϑ= ϑx + ϑ y rr rr⎧⎫1 2 r rr−=00()ϑαcos ti +−⎨⎬ gtj +()ϑα0sin t j ⎩⎭2 rr rr⎡⎤1 2 ⇔−rr00 =ϑα()cos ti +− gt + ϑα0()sin tj ⎣⎦⎢⎥2 mà: r r rhj0 = rr⎡⎤1 2 rtigr cos . ttsinhj . ⇒=⎣⎦⎡⎤ϑα00()+−⎢⎥ + ϑα() + 1442 4 43 ⎣⎦2 x 14444244443 y => phương trình quỹ đạo: ⎧ x xtt=⇒=()ϑαcos ⎪ 0 ϑ cosα M ⎨ 0 (3) 1 ⎪ygtth=−2 +ϑαsin + ⎩⎪ 2 0 g 2 => y =− 22xtgx+()α . +h (4) 2.cosϑα 0 Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH - CHÂU Các vấn đề thường gặp: • Ở độ cao cực đại: (B): tiếp tuyến nằm ngang → ϑ y = 0 ; agnB = ϑ0 sin α ϑBy =0 ⇒ϑBx =ϑ0 cosα = ϑB => t = B g ϑ 2 Ta có: an = => r R ϑ 2 ϑ2cos 2 α B ϑ R =B = 0 B B a g (Vì agrr↓↓ ⇒a =0, ag =n ) tnBB r ϑ 0 gr • Độ cao max: thế tB vào (1) α A M 1 2 r ⇒=−ygt +()ϑα0 sin th + r 2 r r r0 ϑ 1 ϑα22sin ϑαsin ⇒=−y gh.s00 +ϑαin+ gr B 2 gg2 0 C x 1 ϑα22sin 0 ⇒=yh0 + B 2 g • Tại điểm chạm đất (C): 1 * Thời gian chạm đất; ygttht=−2 +ϑαsin + = 0 ⇒ > 0 cc2 0 c c g 2 * Điểm chạm đất cách chân điểm ném: yxtccc= −++22 ()gα .0xh=⇒xc>0 2.cosϑα0 2ϑ0 sinα • Khi ném tại mặt đất (h=0) tC = g 22 2sin.cosϑ00ααϑ sin2α o *Tầm xa : x == ⇒ Để xC max α = 45 C gg 1 ϑ 22sin α *Độ cao cực đại: y = 0 B 2 g * Bán kính cong của quỹ đạo tại C: ( at=gsinα ; an=gcosα ; ϑc=ϑ0 ) 2 2 ϑC ϑo RC = = an g.cosα @Hỏi góc α?: ϑ0 , xC cho trước ⎧α = β xg. ⎧2αβ= ⎪ 1 2 sinβα==C sin 2 ⇒⎨⎨ ⇒ ϑ 2 2α =−πβ β o ⎩ ⎪α =−π ⎩ 2 22 Giảng viên chính ĐHBKTPHCM: Th.S NGUYỄN – MINH - CHÂU 1.8 Phép biến đổi vận tốc – gia tốc: r r r ⎧r= r' + ro ⎪ r r r r r r ⎨ϑ= ϑ' + ϑo ϑt = ϑ' t + ϑn b n b ⎪ar= a r' + a r ⎩ o • Quan niệm cơ học cổ điển: Thời gian có tính tuyệt đối, không phụ thuộc vào hệ quy chiếu. Trong khi vị trí, không gian có tính tương đối, phụ thuộc vào hệ quy chiếu. Xét 2 hệ quy chiếu O, O’ ; và O’ chuyển động tịnh tiến so với O. khi đó chuyển động điểm M đ/v O và O’: r r Or: r =++ ixjykz r r Or':r '=+ ixyjkz ' ' + ' uuuur uuuur uuuuur y’ M ⇒=+OM OO'' O M y hay: r r r r= r' + ro r r r rr ϑ= ϑ' + ϑ o r r r r r ' a= a' + ao r ⎧ϑ : Vận tốc điểm M so với O r r0 x’ ⎪ r 0 ⎨ϑ': Vận tốc điểm M so với O’ x ⎪ r 0 ⎪ϑo : Vận tốc của O’ so với O z’ ⎩ z ⎧ar : Gia tốc điểm M so với O ⎪r ⎨a': Gia tốc điểm M so với O’ ⎪r ⎩ao : Gia tốc của O’ so với O
File đính kèm:
 giao_trinh_vat_ly_dai_cuong_chuong_1_dong_hoc_chat_diem.pdf
giao_trinh_vat_ly_dai_cuong_chuong_1_dong_hoc_chat_diem.pdf

