Giáo trình Toán cao cấp A1

 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
id11701062 pdfMachine by Broadgun Software - a great PDF writer! - a great PDF creator! -   
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Bài 1 Giới hạn và liên tục 
I. SỐ THỰC VÀ HÀM SỐ 
1.Các số thực và ðýờng thẳng thực 
Các số thực là những số có thể biểu diễn dýới dạng thập phân nhý : 
trong ðó dấu ba chấm (… ) chỉ dãy các ký số sau dấu chấm thập phân kéo dài ðến vô 
hạn . 
Các số thực có thể ðýợc biểu diễn về mặt hình học bởi các ðiểm trên 1 ðýờng thẳng, 
ðýợc gọi là ðýờng thẳng thực nhý minh họa dýới ðây: 
Tập hợp tất cả các số thực (hay ðừng thẳng thực ) sẽ ðýợc ký hiệu là R. 
Trên tập hợp các số thực ta có hai phép toán cõ bản + và * với một số tính chất ðại số 
quen thuộc ðã biết . Từ ðó ta cũng có phép toán trừ (-) và phép chia (/) cho số khác 0. 
Ngoài ra trên R ta cũng có một thứ tự thông thýờng và với thứ tự này ta có một số 
tính chất ðýợc viết dýới dạng các bất ðẳng thức nhý sau: 
Nếu a,b, và c là các số thực thì ta có 
a < b a+c <b+c 
a < b a-c <b-c 
a 0 ac <bc 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
a < b và c< 0 bc <ac 
ðặc biệt : a < b -b <-a 
a > 0 > 0 
Nếu (a và b cùng là số dýõng ) 
 hay (a và b cùng là số âm ) 
Thì ta có : 
R có một số tập hợp con quen thuộc là tập hợp các số tự nhiên N ,tập hợp các số 
nguyên Z, và tập hợp các số hữu tỉ Q . Theo thứ tự "bao hàm trong " thì 
N  Z  Q  R 
Các số thực không thuộc Q ðýợc gọi là các số vô tỉ . 
Ký hiệu các khoảng ðoạn và nửa khoảng : 
Với a và b là các số thực , ta ký hiệu : 
(a ,b ) là { x R / a< x <b} 
[ a,b ] là {x R / a <=x <= b} 
[a,b) là {x R / a <= x < b } 
(a ,b ] là { x R / a < x <=b} 
(a, ) là {x R / x > a} 
[a, ) là { x R /x >= a} 
( - ,b) là {x R /x < b } 
( - b] là {x R /x <= b} 
( - , ) là R 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Ghi chú : Ngýời ta còn chứng minh ðýợc rằng R có tính chất ðầy ðủ . Theo tính 
chất này thì mọi tập số thực khác rỗng bị chặn trên ðều có cặn trên ðúng (tức là chặn 
trên nhỏ nhất). Týõng tự , mọi tập số thực khác rỗng bị có chặn dýới ðúng. 
Ký hiệu "giá trị tuyệt ðối”: 
Giá trị tuyệt ðối của một số thực x ,ký hiệu bởi |x|, ðýợc ðịnh nghĩa nhý sau : 
Từ ðó ta có một số tính chất dýới ðây: 
(1) Với mọi 
(2) 
(3) 
(4) 
(5) 
(6) 
(7) 
(8) 
(9) 
(10) 
Lýu ý rằng về mặt hình học ,  x biểu diễn khoảng cách từ ðiểm x ðến ðiểm 0 trên 
ðýờng thẳng thực . Tổng quát hõn là : 
 x-y = khoảng cách giữa x và y 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
2. Hàm số 
 Ðịnh nghĩa: 
Một hàm số f từ một tập D vào IR là một quy tắc cho ứng với mỗi x D là một phần 
tử duy nhất f (x) R. 
Một hàm số thýờng ðýợc cho dýới dạng công thức nhý các ví dụ sau: 
Khi hàm số ðýợc cho bởi một công thức nhý hàm số g(x) ở trên thì tập hợp tất cả các 
x mà g(x) xác ðịnh ðýợc gọi là miền xác ðịnh của hàm số. 
Ví dụ: Miền xác ðịnh của hàm số là tập hợp các số thực x sao cho : 
 x
2
 – 4 0 
 x -2 hay x 2 
Vậy miền xác ðịnh là : ( - , -2 ]  [ 2 , ) 
 Ðồ thị của hàm số: 
Ðồ thị của hàm số f là ðýờng biểu diễn trong mặt phẳng Oxy có phýng trình y=f(x). 
Nó bao gồm tất cả các ðiểm (x , f(x)) với x chạy trong miền xác ðịnh của hàm số. 
Ví dụ : 
1) Ðồ thị hàm số y = x2 
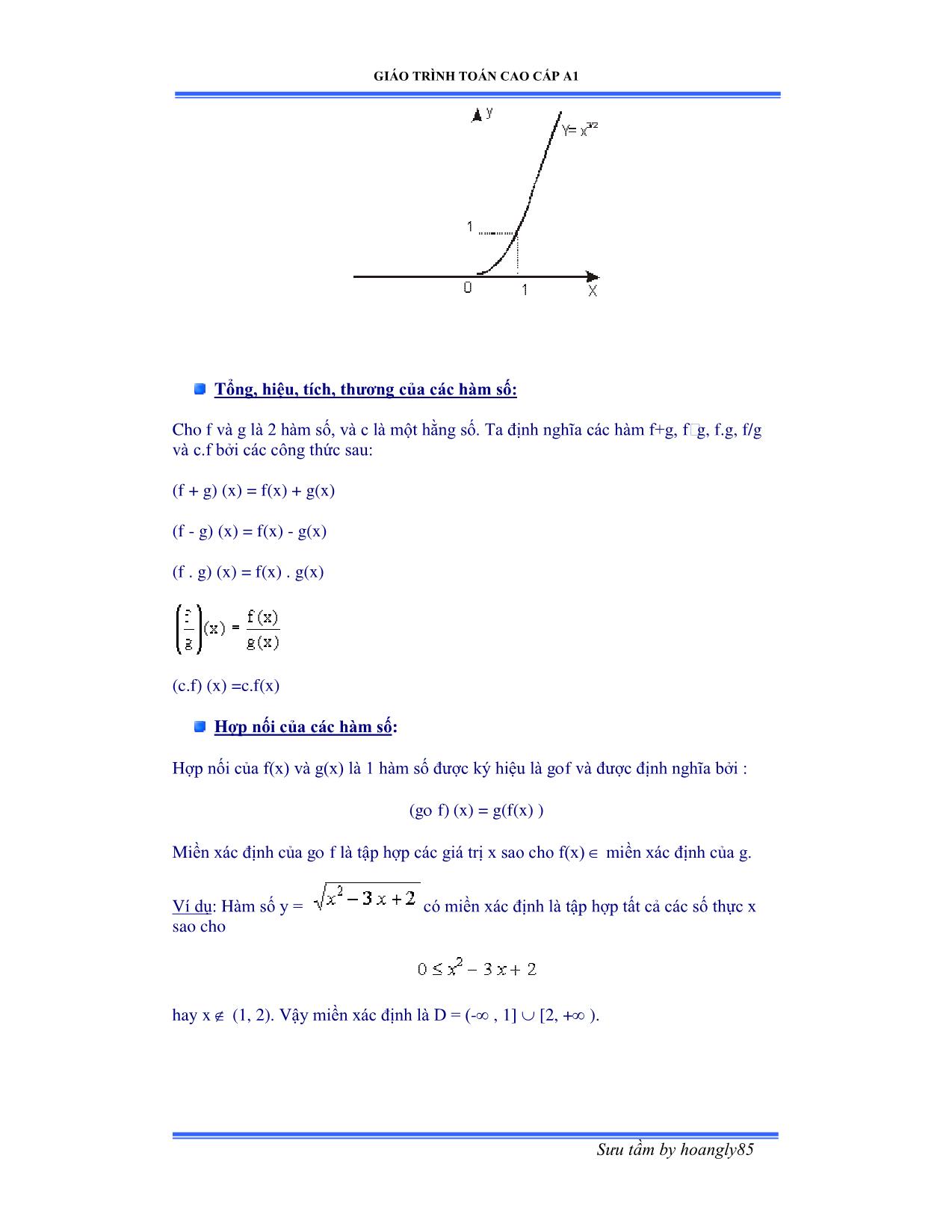
2) Ðồ thị hàm số y = x3/2 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
 Tổng, hiệu, tích, thýõng của các hàm số: 
Cho f và g là 2 hàm số, và c là một hằng số. Ta ðịnh nghĩa các hàm f+g, f–g, f.g, f/g 
và c.f bởi các công thức sau: 
(f + g) (x) = f(x) + g(x) 
(f - g) (x) = f(x) - g(x) 
(f . g) (x) = f(x) . g(x) 
(c.f) (x) =c.f(x) 
 Hợp nối của các hàm số: 
Hợp nối của f(x) và g(x) là 1 hàm số ðýợc ký hiệu là g f và ðýợc ðịnh nghĩa bởi : 
(g f) (x) = g(f(x) ) 
Miền xác ðịnh của g f là tập hợp các giá trị x sao cho f(x) miền xác ðịnh của g. 
Ví dụ: Hàm số y = có miền xác ðịnh là tập hợp tất cả các số thực x 
sao cho 
hay x (1, 2). Vậy miền xác ðịnh là D = (- , 1]  [2, + ). 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
III. CÁC DẠNG VÔ ÐỊNH 
1 . Hàm týõng ðýõng ,VCB ,VCL 
 Ðịnh nghĩa 1: 
Cho hai hàm số f(x)và g(x) không triệt tiêu trong một khoảng quanh xo ( có thể loại 
trừ xo). Ta nói f(x) týõng ðýõng với g(x) khi x -> xo nếu: 
Khi ấy , ta viết : 
f(x)  g(x) khi x -> xo 
Hoặc là : khi x -> xo , f(x)  g(x) 
 Tính chất : Khi x -> xo 
(i) f(x)  g(x) 
(ii) f(x)  g(x) g(x)  f(x) 
(iii) f(x)  g(x) và g(x)  h(x) f(x)  h(x) 
Ví dụ : Khi x -> 0, ta có : 
sin x ~ x ln(1+x) ~ x 
tg x ~ x ex -1 ~ x 
arcsin x ~ x arctg x ~ x 
 Ðịnh nghĩa 2: 
Cho f (x) xác ðịnh quanh xo (có thể loại trừ xo). Ta nói f (x) là một ðại lýợng vô cùng 
bé khi x -> xo viết tắt là VCB , khi 
Trong trýờng hợp ta có (hoặc + , hoặc - ) ta nói f (x) là vô cùng lớn 
(viết tắt là VCL) khi x -> xo 
Ví dụ: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Khi x -> 0 , ta có x, ln(1+x), 1 – ... 
9) 
10) 
11) 
12) (h là hằng số tùy ý) 
 Ví dụ 1: Tính: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
 Ví dụ 2: Tính: 
II. PHÝÕNG PHÁP TÍNH TÍCH PHÂN 
1.Phýõng pháp phân tích 
Tích phân f (x) dx có thể ðýợc tính bằng cách phân tích hàm số f(x) thành tổng của 
các hàm ðõn giản hõn hay dễ tính tích phân hõn : 
f(x) = f1(x) + f2(x) +… +fn (x) 
Và áp dụng công thức : 
 Ví dụ: 
1) 
2) 
3) Tính 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Với n 2: 
Nhờ hệ thức này ta có thể tính In với n tùy ý. 
2. Phýõng pháp ðổi biến 
 Phýõng pháp ðổi biến trong tích phân bất ðịnh có 2 dạng sau ðây : 
 Dạng 1: Giả sử biểu thức dýới dấu tích phân có dạng: 
F(u(x)) . u’(x)dx 
Trong ðó u(x) là một hàm số khả vi. Khi ấy ta có thể ðổi biến bằng cách ðặt u=u(x),và 
có: 
 Dạng 2: Ðặt x = (+) , trong ðó (t) là một hàm khả vi, ðõn ðiệu ðối với biến t, 
ta có : 
 Ví dụ: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
1) Tính: 
Ðặt: u = x2 + 1, du = 2xdx 
2) , với u = sinx 
3) Tính: 
Ðặt u = x2, du = 2xdx hay xdx = 
4) Tính 
Ðặt u = ex. Ta có : du = exdx, và: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
5) Tính 
Ðặt u = cos2x Ta có: 
du = -2cos x sinx dx = -sin 2xdx 
Suy ra: 
6) Tính 
Ðặt: x = sint ; 
 t = arcsin x, ( -1 x 1) 
Ta có: dx = cost dt 
Suy ra 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Mà 
và t = arcsin x 
Nên: 
3.Phýõng pháp tích phân từng phần 
Giả sử u = u(x) và v = v(x) là các hàm số có ðạo hàm liên tục u’= u’(x) và v’= v’(x) : 
Ta biết: 
(u.v)’= u’v+u.v’ 
hay u.v’= (uv)’-v.u’ 
Từ ðó suy ra công thức: 
Công thức này ðýợc gọi là công thức tích phân từng phần , và còn ðýợc viết dýới 
dạng : 
Công thức tích phân từng phần thýờng ðýợc áp dụng trong trýờng hợp hàm dýới dấu 
tích phân có dạng f(x) = u.v’ mà hàm g = v.u’ có tích phân dễ tính hõn. 
Trong một số bài toán, sau khi áp dụng công thức tích phân từng phần ở vế phải lại 
xuất hiện tích phân ðã cho ban ðầu với hệ số khác, tức là : 
Khi ðó ta tính ðýợc : 
 Ví dụ: 
1)Tính 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Ðặt u = ln x 
v’= x 
Áp dụng công thức tích phân từng phần, ta có : 
2) Tính 
Ðặt u = arctg x 
v’= x , 
Ta có : 
Suy ra : 
3) Tính 
Ðặt u = sinx u’ = cos x 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
v’= ex ; v = ex 
Ðể tính: ta ðặt: 
u1 = cos x u’1= -sinx 
v’1= ex v1 = ex 
Suy ra: 
Vậy: 
Suy ra: 
4) Tính (a > 0) 
Ðặt 
v’ = 1 v = x 
Suy ra: 
Ta có: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Do ðó: 
Suy ra 
Vậy: 
5) Tính 
Ðặt ; 
v’=1 v = x 
Suy ra : 
Ta có: 
Suy ra: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
6) Tìm công thức truy hồi ðể tính tích phân 
(a>0) 
Ta có: 
Với n 1, ðặt: 
v’ = 1 v = x 
Suy ra: 
Ta có: 
Suy ra: 
Vậy: 
BÀI TẬP CHÝÕNG 3 
1. Tính các tích phân: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
2.Tính các tích phân: 
3.Tính tích phân bằng phýõng pháp tích phân toàn phần: 
4.Tính tích phân hàm hữu tỉ. 
5. Tính tích phân hàm lýợng giác. 
6. Tính tích phân hàm vô tỉ. 
7. Tính các tích phân sau: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
8. Tính tích phân: 
9. Lập công thức truy hồi và tính tích phân: 
và tính I4 
và tính I6, I7 
10. Tính tích phân: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Bài 5 Tích phân hàm hữu tỉ và hàm lýợng giác 
III. TÍCH PHÂN HÀM HỮU TỈ 
Cho tích phân trong ðó là một phân thức hữu tỉ tối giản theo x. 
Nếu bậc của P(x) bậc của Q(x) thì bằng cách chia ða thức P(x) cho Q(x) ta viết 
ðýợc: 
P(x) = Q(x) . S(x) + R(x), với bậc R(x) < bậc Q(x) 
Do ðó: 
Vì S(x) là một ða thức theo x nên có thể tính ðýợc một cách dễ dàng. Nhý 
vậy ta chỉ cần tìm cách tính với bậc của R(x) < bậc của Q(x). 
Tích phân có thể ðýợc tính bằng cách phân tích phân thức hữu tỉ 
thành tổng của các phân thức hữu tỉ ðõn giản hõn dựa vào 2 mệnh ðề sau ðây. 
 Mệnh ðề 1: Mọi ða thức Q(x) với hệ số thực ðều có thể phân tích thành tích của 
các nhị thức bậc nhất và các tam thức bậc 2 không có nghiệm thực : 
Trong ðó các tam thức x2+ px + q ,… ., x2 + p’x + q’ không có nghiệm thực 
 Mệnh ðề 2: Giả sử phân thức hữu tỉ có bậc của P(x)<bậc của Q(x) và Q(x) 
có dạng 
Trong ðó các tam thức (x2 + px + q),… .,(x2 + p’x + q’) không có nghiệm thực. Khi ấy 
phân thức hữu tỉ có thể phân tích thành tổng của các phân thức ðõn giản hõn nhý sau: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Trong ðó các hệ số A1, … , Am, B1,… ., Bk, M1, N1,… ., Ml, Nl,…… , R1, 
S1,… ..,Rl’,Sl’ là các hằng số, và ta có thể tính ðýợc các hằng số này bằng phýõng pháp 
hệ số bất ðịnh, phýõng pháp trị riêng hay phýõng pháp phân tích từng býớc. (Các 
phýõng pháp này sẽ ðýợc minh họa qua các ví dụ bên dýới). 
Nhý vậy việc tính tích phân ðýợc ðýa về việc tính 2 loại tích phân sau : 
Và: 
với p2 - 4q < 0 ( Tức là x2 + px + q không có nghiệm thực). 
Ðể tính I1 ta chỉ cần ðặt u = x – a 
Ðể tính I2 ta có thể phân tích I2 dýới dạng: 
Tích phân ðýợc tính dễ dàng bằng cách ðặt: u = x2 + px + q. 
Ðối với . Ta biến ðổi x2 + px + q = (x-b)2 + c2 và ðặt u = x – b ðể 
ðýa về dạng: mà ta ðã biết cách tính trong ví dụ 6 ), Mục II.3. 
 Ví dụ : 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
 1) Tính 
x
5 
- x
2 
= x
2(x3 – 1) = x2 (x – 1) (x2 + x + 1) 
Do ðó: 
Nhân 2 vế cho x5 – x2 ta ðýợc: 
Thay x = 0, rồi x = 1 vào ta ðýợc :1 = -B và 1 = 3c 
 B=-1; C = 
Ðồng nhất các hệ số của x4, x3, x2 ở 2 vế của ðẳng thức trên (ðúng với mọi x) ta ðýợc: 
Thay B= -1 và C= vào, rồi giải hệ này sẽ ðýợc: 
Vậy: 
Ta có: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Suy ra: 
 2) Tính 
Phân tích phân thức ta ðýợc: 
Ta có : 
Theo công thức truy hồi trong ví dụ 6) mục II,3, ta có 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Vậy 
 3) Tính 
 Trýớc hết ta ðổi biến ðể ðõn giản hóa tính phân trên bằng cách ðặt u = x2 ,du = 
2xdx 
IV. TÍCH PHÂN HÀM LÝỢNG GIÁC 
 Xét tích phân I = R(sinx, cosx)dx, trong ðó R(u, v) là hàm hữu tỉ ðối với u và v. 
Ðể tính tích phân này ta có thể dùng các phýõng pháp ðổi biến sau : 
1. Phýõng pháp chung 
Ðặt 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
hay 
Ta có: 
Suy ra: 
Tích phân này có dạng tích phân của phân thức hữu tỉ ðã xét trong mục III. 
 Ví dụ: 
 1) Tính: 
Ðặt: #9; 
Suy ra: 
 2) Tính: 
Ðặt: 9; 
Suy ra: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Phân tích phân thức hữu tỉ ta ðýợc: 
2. Một số trýờng hợp ðặc biệt 
(1) Nếu R(-sinx, -cosx) = R(sinx,cosx) 
thì ðặt u=tgxhoặc u=cotgx 
(2) Nếu R(sinx, -cosx) = -R(sinx,cosx) 
thì ðặt u = sinx. 
(3) Nếu R(-sinx, cosx) = -R(sinx,cosx) 
thì ðặt u = cosx 
(4) Tích phân dạng sinmx cosnx dx với m và n là các số chẵn dýõng.Ta có thể ðổi 
biến bằng cách dùng công thức : 
 Ví dụ : 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
 1) Tính: 
Ðặt 
Suy ra: 
 2) Tính: 
Ðặt u = sinx du = cosx dx 
Suy ra: 
 3) Tính: 
Ðặt u = cosx du = -sinx dx. 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
 4) Tính: 
Ta có: 
Suy ra: 
 Chú ý: 
Ðối với các tích phân dạng 
ta dùng các công thức biến ðổi tích thành tổng: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
V. TÍCH PHÂNHÀM HỮU TỈ ÐỐI VỚI X VÀ 
 Xét tích phân , trong ðó R(u,v) là hàm hữu tỉ ðối với u 
và v và a2x + bx + c là một tam thức bậc 2 không có nghiệm kép. 
1. Phýõng pháp tổng quát 
Tùy theo dấu của hệ số a ta ðýa tam thức a2x + bx + c về dạng tổng hay hiệu hai bình 
phýõng . Khi ðó tích phân I có một trong ba dạng sau: 
(a) 
Ðặt: với 
(b) 
Ðặt: , 
(c) 
Ðặt: 
 Ví dụ : 
 1) 
Biến ðổi : x2 + 2x = (x+1)2 - 1 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Xét trýờng hợp x+1 1 
Ðặt 
Ta có: 
Do ðó: 
Mà: 
Trýờng hợp x + 1 < -1 ; công thức (*) ở trên vẫn ðúng vì ðạo hàm của hàm số ở vế 
phải (*) luôn bằng: 
 2) 
Ðặt 
Ta có dx = ( 1 + tg2 t) dt 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Ðặt u = sin x du = cost dt. Khi ðó: 
Mà 
sint và tgt cùng dấu với 
2.Tích phân dạng 
Ðể tính tích phân dạng này ta có thể ðặt : 
3. Tích phân dạng 
Ðể tính các tích phân dạng ta biến ðổi tam thức ax2 + bx + c thành tổng hoặc hiệu của 
hai bình phýõng rồi ðổi biến ðể ðýa về các dạng tích phân ðã biết sau ðây: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
 Ví dụ : Tính các tích phân: 
 1) 
Biến ðổi: x2 - 4x + 5 = (x-2)2 + 1 
Ðặt u = x – 2 du = dx 
Ta có : 
 2) 
Biến ðổi: 3 – 4x – 4x2 = 4 – (2x+1)2 
Ðặt u = 2x + 1 du = 2dx 
Ta có: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
BÀI TẬP CHÝÕNG 3 
1. Tính các tích phân: 
2.Tính các tích phân: 
3.Tính tích phân bằng phýõng pháp tích phân toàn phần: 
4.Tính tích phân hàm hữu tỉ. 
5. Tính tích phân hàm lýợng giác. 
6. Tính tích phân hàm vô tỉ. 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
7. Tính các tích phân sau: 
8. Tính tích phân: 
9. Lập công thức truy hồi và tính tích phân: 
và tính I4 
và tính I6, I7 
10. Tính tích phân: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Bài 6 Một số dạng tích phân khác 
VI. MỘT SỐ DẠNG TÍCH PHÂN KHÁC 
1. Tích phân dạng 
Trong ðó R là một hàm hữu tỉ và m,… ,k là các số nguyên dýõng; a, b, c, d là các hằng 
số 
Ðể tính tích phân này ta gọi x là một bội số chung nhỏ nhất của m,… ,k và ðặt: 
Từ ðó, tích phân sẽ ðýợc chuyển về dạng: 
Trong ðó R1 là một hàm hữu tỉ ðối với u 
 Ví dụ: Tính 
Ðặt 
Ta có: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
2. Tích phân hàm hữu tỉ ðối với eax 
Trong ðó R là một hàm hữu tỉ ðối và a 0 
Ðể tính phân tích này ta ðặt : u = eax 
Khi ðó dx = và: 
Có dạng tích phân hàm hữu tỉ. 
 Ví dụ: 
Ðặt: u = ex du = exdx 
3.Các tích phân có dạng: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Trong ðó p(x) là một ða thức theo biến x. 
Ðể tính các tích phân này ta dùng phýõng pháp tích phân toàn phần bằng cách ðặt : 
u = p(x) 
 Ví dụ: 
Ðặt: 
Suy ra 
4.Các tích phân có dạng : 
Ðể tính các tích phân này ta dùng phýõng pháp tích phân toàn phần bằng cách ðặt: 
dv= p (x) dx 
 Ví dụ: Tính xarctgxdx 
Ðặt u = arctgx 
du= xdx , 
Suy ra 
Ta có 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Vậy: 
VII. MỘT SỐ TÍCH PHÂN KHÔNG BIỂU DIỄN ÐÝỢC 
 DÝỚI DẠNG HÀM SÕ CẤP 
Nếu hàm số f(x) liên tục trên (a,b) thì f (x) luôn luôn có nguyên hàm trên khoảng ðó , 
tức là tích phân f(x) dv tồn tại . Tuy nhiên có một số tích phân không thể biểu diễn 
dýới dạng hàm sõ cấp , chẳng hạn các tích phân nhý sau ðây: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Bài 7 Tích phân xác ðịnh 
I. ÐỊNH NGHĨA VÀ CÁC TÍNH CHẤT 
1.Ðịnh nghĩa 
Cho hàm f(x) trên ðoạn [a.b]. Chia ðoạn [a.b] một cách tùy ý thành n ðoạn nhỏ bởi 
các ðiểm a = xo < x1 < …… < xn = b. Ðặt xi = xi – xi-1 và trên 
[ xi
-1, xi ] lấy một ðiểm ti tùy ý, i = 1, 2 , … , n. Lập tổng 
Và gọi Sn
là tổng tích phân của hàm f(x) trên ðoạn [a,b] . Nếu Sn có giới hạn hữu hạn 
I khi n sao cho max{ xi
} 0 và I không phụ thuộc vào cách chia ðoạn [a,b] 
và cách chọn các ti, thì I ðýợc gọi là tích phân xác ðịnh của f(x) trên ðoạn [a,b] và 
ðýợc ký hiệu là: 
Vậy: 
Khi ðó ta nói f(x) là khả tích trên [a,b]; [a,b] là khoảng lấy tích phân, a là cận dýới, b 
là cận trên , f là hàm dýới dấu tích phân và x là biến tích phân. 
 Chú ý : 
(i) chỉ phụ thuộc f và các cận a, b mà không phụ thuộc vào biến tích phân, tức 
là: 
(ii) Trýờng hợp a > b , ta ðịnh nghĩa : 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
(iii) Trýờng hợp a = b, ðịnh nghĩa 
(iv) Từ ðịnh nghĩa, ta thấy ngay hàm f(x) bị chặn trên [a,b] nếu f(x) khả tích trên [a,b]. 
 Ý nghĩa hình học: 
Nếu f(x) 0 trên [a,b] và f(x) khả tích trên [a,b] thì chính là diện tích S của 
hình thang cong giới hạn bởi các ðýờng : 
x = a; x = b; y = f(x) và trục hoành y=0. 
2.Các tính chất 
(1) 
(2) 
(3) Nếu 
Hệ quả: 
(4) Với c [a,b] ta có: 
(5) Giả sử f(x) khả tích trên [-a, a]. Khi ðó: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
nếu f(x) là hàm số chẵn 
 nếu f (x) là hàm số lẻ 
3.Tổng Darboux & ðiều kiện khả tích 
Do hàm khả tích thì bị chặn nên ta chỉ xét các hàm bị chặn trên [a, b]. Mỗi phép chia 
nhỏ ðoạn [a,b] bởi các ðiểm a = xo < x1 < …… < xn ðýợc gọi là một phân hoạch 
của[a,b] , ký hiệu P = { xo, x1…… . xn }. Ðặt: 
(cận trên ðúng cuả f(x) trên [ xi
-1, xi ] ) 
(cận dýới ðúng cuả f(x) trên [ xi
-1, xi ] ) 
Ta gọi U(f,P) và L(f,P) là các tổng (Darboux) trên và dýới của f ứng với phân hoạch 
P. Ngýời ta ðã chứng minh ðýợc một ðiều kiện khả tích ðýợc phát biểu trong ðịnh lý 
sau ðây : 
 Ðịnh lý 1: Ðiều kiện cần và ðủ ðể f khả tích là: 
Từ ðịnh lý này ta có thể chứng minh một số lớp hàm khả tích ðýợc phát biểu trong 
các ðịnh lý dýới ðây. 
 Ðịnh lý 2: Hàm f(x) liên tục trên [a,b] thì khả tích trên [a,b]. 
 Ðịnh nghĩa: 
Nếu hàm số f(x) xác ðịnh tại xo và không liên tục tại xo nhýng có giới hạn 2 phía tại xo 
thì ta nói xo là ðiểm gián ðoạn loại 1 tại xo. 
 Ðịnh lý 3: 
Nếu f chỉ có hữu hạn ðiểm gián ðoạn loại 1 trên [a,b] thì f khả tích trên [a,b]. 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
 Ðịnh lý 4: Hàm bị chặn và ðõn ðiệu trên [a,b] thì khả tích trên [a,b]. 
II- LIÊN HỆ GIỮA TÍCH PHÂN XÁC ÐỊNH VÀ NGUYÊN HÀM 
1.Tích phân xác ðịnh nhý hàm của cận trên 
Cho f là một hàm khả tích trên [a ,b ]với x [ a , b ], 
Xác ðịnh và là một hàm số theo biến x. Hàm số này ðã ðýợc chứng minh là có những 
tính chất phát biểu trong mệnh ðề sau ðây: 
 Mệnh ðề: 
(i) Nếu f khả tích trên [a,b] thì F(x)= là hàm liên tục trên [a,b]. 
(ii) Nếu f(t) liên tục tại t = xo (a,b), thì F(x) có ðạo hàm tại xo và F’(xo)=f(xo). 
 Nhận xét : 
Nếu f liên tục trên [a,b] thì hàm số là nguyên hàm của f trên [a,b]. 
2.Ðịnh lý cõ bản 
 Ðịnh lý : Giả sử f liên tục trên [ a,b]. Khi ðó : 
(i) là một nguyên hàm của f(x) trên [a,b]. 
(ii) Nếu G(x) là một nguyên hàm bất kỳ của f(x) trên [a,b] thì: 
(Công thức này ðýợc gọi là công thức Newton-Leibnitz) 
Chứng minh: Ta chỉ cần chứng minh phần (ii). 
Do F(x) và G(x) là các nguyên hàm của f(x) trên [a,b] nên ta có hằng số C sao cho 
F(x) = G(x) + C,  x [a,b]. Cho x = a ta ðýợc 0 = G(a) + C, suy ra: 
G(a) = - C 
Vậy F(b) = G(b) - G(a), tức là: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
Hiệu số G(b) - G(a) trong công thức Newton-Leibnitz của ðịnh lý trên thýờng ðýợc 
viết dýới các ký hiệu sau: 
, hay vắn tắt là 
hay vắn tắt là 
 Ví dụ:Tính tích phân xác ðịnh : 
1) 
2) 
  
3) 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
BÀI TẬP CHÝÕNG 4 
1.Tính các tích phân : 
2/ Tính các tích phân : 
3. Tính tích phân suy rộng: 
4. Tính diện tích hình phẳng giới hạn bởi các ðýờng 
5. Tính thể tích khối tròn xoay do hình phẳng giới hạn bởi: 
 GIÁO TRÌNH TOÁN CAO CẤP A1 
Sýu tầm by hoangly85 
6. Một hình cầu bán kính R và một nón tròn xoay có bán kính ðáy r và ðýờng cao h > 
R sao cho ðỉnh nón trùng với tâm cầu. Tìm thể tích phần giao của hai hình. 
7. Tính ðộ dài ðýờng cong: 
8. tính diện tích mặt tròn xoay: