Giáo trình Dao động kỹ thuật
Biểu diễn các hàm tuần hoàn trong miền tần số
Ta chọn hệ toạ độ vuông góc, trục hoành biểu diễn tần số ω (hoặc tần số f), trục
tung biểu diễn độ lớn các biên độ A của các điều hoà. Việc biểu diễn các biên độ Ak
ứng với tần số ωk = kω của điều hoà thứ k trong chuỗi Fourier của hàm tuần hoàn y(t)
trong mặt phẳng 𝜔, 𝐴 gọi là biểu diễn hàm tuần hoàn y(t) trong miền tần số. Tập hợp
các biên độ Ak trong khai triển Fourier (2.20) của hàm tuần hoàn y(t) đƣợc gọi là phổ
của hàm tuần hoàn y(t). Trên hình 1.10 biểu diễn phổ của hàm răng cƣa trong thí dụ 1.1.
Việc cho biết các biên độ Ak của các điều hoà chƣa đủ các thong tin về hàm
y(t), bởi vì ta chƣa biết đƣợc các pha ban đầu của các điều hoà đó. Tuy nhiên từ biểu
đồ biên độ - tần số ta cũng có thể giải quyết đƣợc khá nhiều vấn đề của bài toán dao
động cần nghiên cứu. Từ kết quả đo dao động, các máy phân tích tần số đơn giản cũng
có thể xác định đƣợc biên độ của dao động cơ bản và các dao động bậc cao. Việc xác
định các pha ban đầu đòi hỏi các thiết bị đo tƣơng đối phức tạp.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
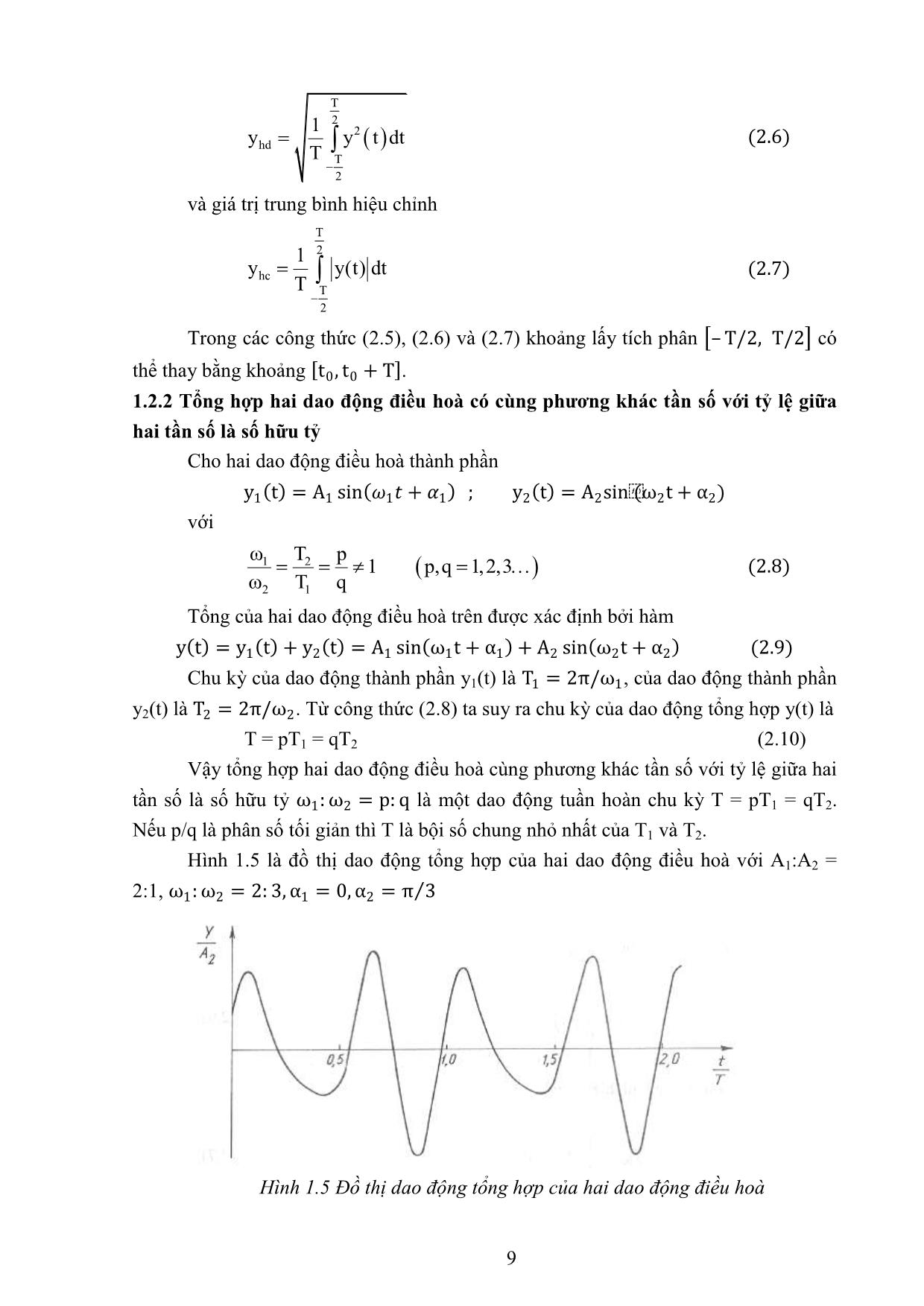
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Giáo trình Dao động kỹ thuật

LỜI NÓI ĐẦU Dao động là một hiện tƣợng phổ biến trong tự nhiên và trong kỹ thuật. Các máy móc, các phƣơng tiện giao thông vận tải, các toà nhà cao tầng, những chiếc cầu bắc qua các dòng sông, chiếc đồng hồ đeo tay mà chúng ta thƣờng hay sử dụng đó là các hệ dao động trong kỹ thuật. Bản thân mỗi ngƣời chúng ta cũng là một hệ dao động mà có lẽ ít ngƣời đã biết. Vậy dao động là gì? Một cách sơ lƣợc, dao động là một quá trình trong đó một đại lƣợng vật lý (hoá học, sinh học,) thay đổi theo thời gian mà có một đặc điểm nào đó lặp lại ít nhất một lần. Dao động kỹ thuật là dao động của các hệ kỹ thuật (các máy móc, các phƣơng tiện giao thông vận tải,). Các kiến thức về lý thuyết dao động ngày nay trở thành một bộ phận không thể thiếu đƣợc trong tổng thể các kiến thức cần phải trang bị cho ngƣời kỹ sƣ cơ khí, xây dựng, tự động hoá, Nhằm đáp ứng yêu cầu cần thiết đó môn học Dao động kỹ thuật đã đƣợc đƣa vào chƣơng trình giảng dạy cho sinh viên trƣờng Đại học Sƣ phạm Kỹ thuật Nam Định, nội dung môn học gồm hai phần: Dao động tuyến tính của hệ hữu hạn bậc tự do và Dao động tuyến tính của hệ vô hạn bậc tự do trong tổng số 4 chƣơng của chƣơng trình môn học. Tập bài giảng đƣợc viết trên cơ sở chƣơng trình môn học Dao động kỹ thuật. Ngƣời biên soạn đã cố gắng trình bày những vấn đề cơ bản của Dao động kỹ thuật theo quan điểm hiện đại, đảm bảo tính sƣ phạm và yêu cầu chất lƣợng của một bài giảng giảng dạy đại học. Những kiến thức trình bày trong bài giảng này là những kiến thức tối thiểu, cần thiết để sinh viên có thể học các môn học tiếp theo của các ngành Công nghệ hàn, Công nghệ Ô tô, Công nghệ chế tạo máy Các Ví dụ trong bài giảng gồm hai loại: Các Ví dụ củng cố kiến thức và các Ví dụ áp dụng giải một số mô hình dao động trong kỹ thuật. Tập bài giảng đƣợc biên soạn lần đầu nên chắc chắn còn nhiều thiếu sót. Chúng tôi rất mong nhận đƣợc sự góp ý của các đồng nghiệp và các em sinh viên để có điều kiện sửa chữa, hoàn thiện hơn tập bài giảng nhằm phục vụ tốt hơn cho công tác giảng dạy và học tập. Các ý kiến đóng góp xin gửi về địa chỉ: Bộ môn Kỹ thuật cơ sở, Khoa cơ khí, Trƣờng Đại học Sƣ phạm kỹ thuật Nam Định. Nhóm tác giả biên soạn 1 MỤC LỤC LỜI NÓI ĐẦU ................................................................................................................. 1 MỤC LỤC ....................................................................................................................... 2 Chƣơng 1 ......................................................................................................................... 4 MÔ TẢ ĐỘNG HỌC CÁC QUÁ TRÌNH DAO ĐỘNG ................................................ 4 1.1 DAO ĐỘNG ĐIỀU HOÀ ...................................................................................... 4 1.1.1 Biểu diễn thực dao động điều hoà .................................................................. 4 1.1.2 Biểu diễn phức dao động điều hoà ................................................................. 5 1.1.3 Tổng hợp hai dao động điều hoà cùng phƣơng và cùng tần số ...................... 6 1.2 DAO ĐỘNG TUẦN HOÀN ................................................................................. 7 1.2.1 Các tham số động học của dao động tuần hoàn ............................................. 7 1.2.2 Tổng hợp hai dao động điều hoà có cùng phƣơng khác tần số với tỷ lệ giữa hai tần số là số hữu tỷ .............................................................................................. 9 1.2.3 Phân tích Fourier các hàm tuần hoàn ........................................................... 11 1.2.4 Biểu diễn các hàm tuần hoàn trong miền tần số ........................................... 14 1.2.5 Biểu diễn đồng thời hai đại lƣợng dao động điều hoà theo hai phƣơng vuông góc với nhau .......................................................................................................... 14 1.2.6 Biểu diễn dao động tuần hoàn trên mặt phẳng pha ...................................... 18 1.3 DAO ĐỘNG KHÔNG TUẦN HOÀN ................................................................ 20 1.3.1 Tổng hợp hai dao động điều hoà cùng phƣơng khác tần số với tỷ lệ giữa hai tần số là số vô tỷ .................................................................................................... 20 1.3.2 Biểu diễn tích phân Fourier các hàm không tuần hoàn ................................ 22 1.3.3 Dao động họ hình sin .................................................................................... 25 CÂU HỎI ÔN TẬP ....................................................................................................... 29 Chƣơng 2 ....................................................................................................................... 30 DAO ĐỘNG TUYẾN TÍNH CỦA HỆ MỘT BẬC TỰ DO ........................................ 30 2.1 DAO ĐỘNG TỰ DO KHÔNG CẢN ......... ... sau: 4 3 2 x x x x f x a3 a 2 a 1 a 0 l l l l Trong đó: các hằng số ai đƣợc chọn sao cho f(x) thoả mãn các điều kiện biên. Các điều kiện biên có dạng: x = 0; f(0) = 0; f’(0) = 0; x = 1; f”(1) = 0; f”’(1) = 0 Từ các điều kiện biên trên ta dễ dàng xác định các hằng số ai. a0 = 0; a1 = 0; a2 = 6; a3 = -4 Vậy hàm f(x) có dạng 162 4 3 2 x x x f(x) 4 6 l l l Thế f(x) vào tử số và mẫu số của công thức (3.81) ta có 242 1 1 12 x 144 EI 1 x 144 EI EIf"2 ( x ) dx EI 1 dx 1 dx 2 ll 4 5 3 0 0 l l 0 l 4322 11 x x x lf22( x ) dx mf ( l ) 4 6 dx 9 m l l l 00 104 1 l 9 m 104 l 405 m 45 45 Từ đó suy ra: (144 45)EI 1296 EI 2 R 5l33 (104 l 405 m ) l (104 l 405 m ) Để kiểm tra độ chính xác của công thức Rayleigh, ta xét trƣờng hợp m = 0,75l. Khi đó 1296EI 1296 EI EI 2 3,1784 R l3(104 l 405.0,75 l ) 407,75 l 4 l 4 Do đó: EI 1,7828 R l4 EI Trong thí dụ 4.7 ta tính đƣợc: 1,742 . Vậy sai số là 2,3% R l4 Trƣờng hợp m = 0, ta có 1296 EI EI EI 2 12,46 3,53 RR104 l4 l 4 l 4 Giá trị chính xác của tần số riêng cơ bản theo công thức (3.37) là EI EI 2 12,36 3,516 11ll44 vậy sai số là: 0,4%. Nhƣ vậy, tần số riêng cơ bản theo công thức Rayleigh khá gần với tần số riêng tính chính xác. b. Phương pháp Ritz Tƣơng tự nhƣ tính toán ở phần trên, ta có biểu thức động năng cực đại và thế năng cực đại của dầm dao động uốn nhƣ sau: 163 2 1 1 2 1 2 Tmax ()() x X x dx , max EI x X'' ( x ) dx 2 0 2 0 Trong đó X(x) là hàm riêng. Nếu ta thay gần đúng hàm riêng bằng hàm f(x) X(x) = f(x) = a1f1(x) + a2f2(x) + + anfn(x) (3.82) Thì từ đẳng thức: Tmax - max = 0 ta suy ra 1 2 22 I()"()()() x f x x f x dx 0 E Trong đó: là một hằng số Theo phƣơng pháp Ritz ta chọn các hàm f1(x), f2(x), thoả mãn các điều kiện biên, còn các hằng số a1, a2, đƣợc chọn sao cho hằng số là bé nhất. Nhƣ thế bài toán dẫn đến tìm các hằng số a1, a2,, an sao cho phiếm hàm. 1 2 22 I()"()()() x f x x f x dx 0 E đạt cực trị. Thế biểu thức (3.82) vào (3.83) ta đƣợc 1 nn2 2 " (,,...,)aa a Ix () afx () () x afxdx () 12 n k k E k k 0 kk 11 Điều kiện cần để hàm (a1,a2 ,...,an ) đạt cực trị là 0 j 1,2,..,n (3.84) a j Chú ý đến biểu thức (3.83) hệ phƣơng trình (3.84) có thể viết dƣới dạng 1 2 22 Ixfx( ) " ( ) ( xfxdx ) ( ) 0, j 1,2,..., n (3.85) aEj 0 Do hàm f(x) có dạng nhƣ biểu thức (3.82) nên hệ phƣơng trình (3.85) là một hệ phƣơng trình đại số tuyến tính thuần nhất đối với các ẩn a1, a2, , an. Từ điều kiện cần để cho a1, a2, , an không đồng nhất bằng không, ta suy ra phƣơng trình đặc trƣng để xác định các tần số riêng của hệ. Thí dụ 4.9: Cho dầm công xôn có bề dày b = b0 không đổi, một đầu ngàm chặt, một đầu tự do (Hình 4.23). Hãy xác định tần số riêng cơ bản bằng phƣơng pháp Rayleigh và phƣơng pháp Ritz, tần số riêng bậc một bằng phƣơng pháp Ritz. Lời giải: Từ hình vẽ 4.23 ta dễ dàng tính đƣợc diện tích thiết diện A(x) và mômen quán tính mặt I(x). 3 x 1 3 x A(x) bh0 , I(x) bh0 l 12 l 164 O h0 x b0 l Hình 4.23 Hình thí dụ 4.9 Các điều kiện biên có dạng: d 2 X d d 2 X x = 0; EI 0, EI 0 (3.86) 2 2 dx dx dx dX x = l X 0, 0 (3.87) dx Để thoả mãn các điều kiện biên ta chọn dạng đƣờng cong uốn nhƣ sau: 2 2 x x X (x) f (x) a1 1 a2 1 ... (3.88) l l Dễ dàng nhận thấy rằng các số hạng của chuỗi (3.88) và đạo hàm của nó đối với x bằng không khi x = l Do đó các điều kiện biên (387) đƣợc thoả mãn. Các điều kiện biên (3.86) cũng đƣợc thoả mãn vì I(x) và dI(x)/dx bằng không khi x = 0. Trƣớc hết ta tính tần số riêng cơ bản dao động uốn của dầm công xôn bằng phƣơng pháp Rayleigh. Ta lấy xấp xỉ: 2 x X (x) f (x) a1 1 (3.89) l 2a Từ đó suy ra: f "(x) 1 l 2 Bây giờ ta tính các tích phân ở tử số và mẫu số của công thức Rayleigh (3.81) 11Ebh3 a 2 Ebh 3 a 2 230 1 0 1 EI()"() x f x dx 7 x dx 3 003l 12l 1 14 22 1 2 2xx bh0 a 1 4 bh 0 a 1 l (xfxdx ) ( ) bha01 1 dx 5 xxldx ( ) 0 0ll l 0 30 5Eh2 1,581 h E Từ đó suy ra: 2 00 RR2 ll42 Ngƣời ta tính đƣợc giá trị chính xác của 1 là 165 1,584h E 0 1 l2 Sai số của k là 3%. Để áp dụng phƣơng pháp Ritz ta chọn 2 2 x x X (x) f (x) a1 1 a2 1 (3.90) l l 2a x Từ đó suy ra: f "(x) 1 a a (3 2) 2 1 2 l l Thế vào biểu thức (3.83) ta đƣợc 1 3 2 2 2 1 3 x 4 x 3 x x x x bh0 a1 a2 3 2 bh0 a1 1 a2 1 dx 12 l l 4 l E l l l l 0 bh3 1 1 l 4 1 1 l 4 1 2 l 4 0 a2 a2 a a 3 1 2 1 2 l 12 30 h 30 280 h 15 105 h Từ điều kiện 0, 0 a1 a2 Ta nhận đƣợc hệ hai phƣơng trình đại số tuyến tính thuần nhất 1 1 1 2 a a 0 6 15 1 15 105 2 (3.91) 1 2 1 1 a1 a2 0 15 105 15 140 4 l với 2 Eh0 Từ điều kiện định thức của hệ phƣơng trình (3.91) bằng không, ta nhận đƣợc phƣơng trình đặc trƣng. 2 – 27,3 + 58,8 = 0 Từ đó suy ra: 1,536h E 5,00h E 0 , 0 l 2 2 l 2 So với nghiệm chính xác, sai số của 1 là 0,13%, sai số của 2 là 14%. Muốn nhận đƣợc giá trị 2 chính xác hơn ta cần chọn xấp xỉ (3.90) với nhiều số hạng hơn. MỘT SỐ BÀI TOÁN MỞ RỘNG VỀ DAO ĐỘNG UỐN CỦA DẦM EULER-BERNOULLI a. Dao động uốn của dầm chịu tác dụng của lực dọc 166 Trƣớc hết xét bài toán dao động uốn của dầm chịu tác dụng của lực dọc F . Giả thiết dầm bị lực dọc nén nhƣ hình vẽ. Cho biết độ cứng chống uốn là EI(x), khối lƣợng trên một đơn vị dài của dầm là (x) = A(x), A(x) là diện tích mặt cắt ngang của dầm. Hình 4.24 Dầm chịu tác dụng lực dọc Xét một phân tố thanh dài dx chịu tác dụng của các lực nhƣ hình 4.24b. Để thiết lập phƣơng trình dao động uốn của dầm ta áp dụng nguyên lý d’Alembert. Từ điều kiện cân bằng các lực theo phƣơng z ta có: Q Qcos ( Q dx )cos( dx ) N sin xx (3.92) Nw 2 (N dx )sin( dx ) ( x ) dx 0 xx t2 Do nhỏ thay cos 1, cos( dx) 1, sin , sin( dx) dx x x x vào (3.92) ta đƣợc 2w Q (x) (N ) (3.93) t 2 x x Trong các tài liệu về sức bền vật liệu, ta có các hệ thức M w Q EI (x) , (3.94) x x x x Thế (3.94) vào (3.93) ta đƣợc phƣơng trình vi phân dao động uốn của dầm chịu tác dụng của lực dọc nén ở đầu dầm 2w 2 2w w (x) EI (x) N(x,t) 0 (3.95) 2 2 2 t x x x x Do độ võng của dầm nhỏ, ta có thể sử dụng giả thiết gần đúng lực dọc trục không thay đổi dọc theo chiều dài dầm. Với giả thiết đó ta có N(x,t) = -F. Nếu dầm là đồng chất, thiết diện không đổi và bỏ qua ngoại lực p(x,t) ta có phƣơng trình dao động uốn tự do của dầm chịu tác dụng của lực nén ở đầu dầm. 2w 2w 2w EI F 0 (3.96) t 2 x4 xx 167 Áp dụng phƣơng pháp khai triển theo các dạng riêng ta tìm nghiệm phƣơng trình (3.96) dƣới dạng x w(x,t) sin(k )Tk (t) (3.97) k 1 l Thế biểu thức (3.97) vào phƣơng trình (3.96) và chú ý đến tính trực giao của các hàm riêng ta đƣợc hệ các phƣơng trình vi phân thƣờng 4 2 EI F Tk l k Tk 0, k 1,2,... (3.98)) l l Từ đó suy ra biểu thức xác định các tần số riêng 4 2 EI F k k k (3.99) l l 2 EI F Nếu đƣa vào ký hiệu: Fk (k ) 4 1 (3.100) Al Fk EI Nhƣ đã biết F 2 là lực giới hạn tĩnh. Ta nêu ra một vài nhận xét từ 1 l 2 phƣơng trình (3.98) và (3.100). - Khi lực dọc tăng trong khoảng 0 < F < F1 thì các tần số riêng sẽ giảm. - Khi F = F1 thì 1 = 0. - Khi F > F1 nghiệm sẽ tăng theo luật số mũ và vị trí cân bằng của dầm sẽ không ổn định. Ta có thể sử dụng điều kiện 1 = 0 làm tiêu chuẩn ổn định động lực đối với dầm bị uốn chịu tác dụng của lực dọc. Khi lực nén đầu dầm không phải là hằng số mà là hàm của thời gian ˆ F(t) F0 F cos(t) , với tần số lực kích động nhỏ hơn nhiều so với tần số riêng đầu tiên dao động dọc của dầm (do đó có thể bỏ ảnh hƣởng dao động dọc), ta có thể thay N(x,t) = -F(t). Phƣơng trình (3.95) bây giờ có dạng 2w 4w 2w EI (F Fˆ cos(t)) 0 (3.101) t 2 x4 0 x2 Ta tìm nghiệm phƣơng trình (3.101) dƣới dạng k x w (x,t) sin .q (t) (3.102) k l k Thế (3.102) vào (3.101) ta nhận đƣợc phƣơng trình vi phân xác định qk(t) 2 k ˆ qk Fk F0 F cos(t)qk 0 (3.103) l EI Trong đó: F (k )2 , k 1,2,... k l 2 168 Nếu dầm đặt trên nền đàn hồi tuyến tính với hệ số cứng k và chịu tác dụng của lực dọc trục thì phƣơng trình dao động uốn của dầm có dạng 2w 2 2w w (x) EI (x) N(x,t) kw 0 (3.104) 2 2 2 t x x x x b. Dao động uốn tương đối của dầm gắn trên đĩa quay Bây giờ ta chuyển sang xét bài toán dao động uốn tƣơng đối của dầm quay đều. Đây là lớp bài toán hay gặp trong thực tế. Dao động uốn của cánh tua bin, dao động uốn của các cánh rôto của máy bay trực thăng. Ký hiệu chiều dài dầm là l, độ cứng chống uốn EI = const, khối lƣợng đơn vị dài của dầm = A = const. Xét dao động uốn tƣơng đối trong mặt phẳng vuông góc với trục quay. Trục rôto quay đều với vận tốc góc . Giả thiết biến dạng góc nhỏ w’(x,t) << 1. Do đó có thể bỏ qua ảnh hƣởng của lực quán tính Coriolis, chỉ quan tâm đến ảnh hƣởng của lực quán tính theo (lực ly tâm). Xét mô hình dao động nhƣ hình 4.25. Áp dụng nguyên lý d’Alembert, từ điều kiện cân bằng các lực theo trục z ta có: 2w Q dx 2 Fz Q cos (Q dx)cos( dx) t x x (3.105) N N sin (N dx)sin( dx) 0 x x Lực quán tính ly tâm của phần tử dầm dx là F(x) = dxr(x)2. Từ đó suy ra (hình 4.25a) 2 Fz(x) = F(x)sin = wdx (3.106) Hình 4.25 Dầm gắn trên đĩa quay Thế biểu thức (3.106) vào (3.105) và thay thế cos 1, cos( dx) 1, x sin , sin( dx) dx ta đƣợc x x 169 2w 4w w EI N(x,t) 2w 0 (3.107) 2 4 t x x x Lực pháp tuyến N(x,t) có thể tính theo đoạn dầm từ mặt cắt x đến mặt cắt l. 1 1 N(x,t) (R x)2dx 2 (1 x)(2R 1 x) (3.108) 0 2 Thế (3.108) vào (3.107) ta nhận đƣợc phƣơng trình vi phân dao động uốn tƣơng đối của dầm quay đều. 2w 4w 1 w EI 2 (1 x)(2R 1 x) w 0 (3.109) 2 4 t x 2 x x Việc giải các phƣơng trình vi phân dao động uốn của dầm chịu tác dụng của lực dọc trục và phƣơng trình vi phân dao động uốn tƣơng đối của dầm gắn trên đĩa quay đều đƣợc xét một cách chi tiết trong cuốn Bài tập dao động kỹ thuật [12]. Trong đó ta thấy các tần số riêng của dầm quay đều lớn hơn so với tần số riêng của dầm không quay. Hiệu ứng này đƣợc gọi là hiệu ứng gia cố độ cứng động lực. 170 CÂU HỎI ÔN TẬP 1. Thiết lập phƣơng trình tần số của thanh đồng chất có tiết diện không đổi có đầu trái ngàm, đầu phải chịu liên kết với lò xo cos độ cứng c0 nhƣ hình 4.26. Xác định hai tần số riêng đầu tiên nếu c0 = EA / l. x c0 Hình 4.26 Hình bài tập 1 2. Đầu trái của thanh đồng chất có tiết diện không đổi gắn với một lò xo có độ cứng k, đầu kia tự do (Hình 4.27). a. Viết phƣơng trình xác định tần số dao động b. Xác định hai tần số đầu của thanh biết k = EA /l. k u x Hình 4.27 Hình bài tập 2 3. Cả 2 đầu thanh đều gắn lò xo nhƣ hình 4.28. Lập phƣơng trình xác định tần số dao động của thanh. Tính hai tần số riêng đầu tiên khi k1 = 2k2 = EA/l. k1 E, A, l k2 x Hình 4.28 Hình bài tập 3 4. Một thanh đồng chất chuyển động dọc theo trục x với vận tộc v không đổi (hình 4.29). Thanh bị va chạm vào một vật chắn, rắn tuyệt đối sao cho từ đó trửo đi mút trái của thanh luôn luôn gắn cứng vào vật rắn. Tính giá trị dịch chuyển cực đại ở đầu phải của thanh và giá trị ứng lực dọc cực đại ở đầu trái của thanh. v E, A, l x Hình 4.29 Hình bài tập 4 5. Cho biết thanh bị kéo bởi một lực P không đổi và ở một thời điểm nhất định, lực đƣợc bỏ đi đột ngột (hình 4.30). Tìm quy luật dịch chuyển của đầu mút phải của thanh. 171 E, A, l P x u0 Hình 4.30 Hình bài tập 5 6. Hãy xác định hàm riêng của dao động dọc của thanh đồng chất có chiêu dài l mang khối lƣợng m ở một đầu còn đầu kia tự do. E, A, l m x Hình 4.31 Hình bài tập 6 7. Tính các tần số riêng và hàm riêng của dao động xoắn của trục đƣợc cho trên hình a, b, c. Trục có tiết diện tròn, mật độ và môđun cắt vật liệu G. l a) l/2 b) c) Hình 4.32 Hình bài tập 7 8. Xác định tần số dao động riêng của trục có tiết diện ngang tròn mang 2 đĩa ở đầu (hình 4.33). Cho biết mômen quán tính của đĩa bằng J1, J2 trục có mật độ khối và mômen quán tính cực của tiết diện Ip. J1 J2 l Hình 4.33 Hình bài tập 8 9. Xác định dao động dọc cƣỡng bức của thanh một đầu ngàm chặt, ở đầu kia chịu tác dụng của lực F(t) = F0sin(t) (hình 4.34). 172 10. Một thanh có một đầu tự do, một đầu chịu kích động động học theo luật u=u0sin(t) nhƣ hình 4.35. Xác định dao động dọc bình ổn của thanh. 11. Một thanh có đầu dƣới mang khối lƣợng m, đầu trên dịch chuyển theo phƣơng thẳng đứng với luật u0 = Usint. Hãy tìm dao động dọc bình ổn của thanh và biên độ dao động dọc của khối lƣợng m (hình 4.36). u0sint u0(t) x x A,E l F0sint Hình 4.34 Hình 4.35 m Hình 4.36 12. Thiết lập phƣơng trình vi phân uốn tự do của dầm và xác định các tần số riêng đối với các mô hình trên hình 4.37. Cho biết dầm đồng chất có tiết diện không đổi, độ cứng chống uốn EI, khối lƣợng đơn vị dài là μ . a c b d Hình 4.37 Hình bài tập 12 13. Thiết lập phƣơng trình dao động tự do của dầm đàn hồi năm trên nền đàn hồi (hình 4.38). Biết rằng phản lực của nền tác dụng lên mỗi đơn vị chiều dài của dầm tỷ lệ bậc nhất với độ võng của dầm là kw (k là hệ số độ cứng của nền). Hãy tìm tần số riêng cho hai trƣờng hợp sau: x x w a) b) Hình 4.38 Hình bài tập 13 173 TÀI LIỆU THAM KHẢO [1] Nguyễn Văn Khang, Dao động kỹ thuật, NXB Khoa học và Kỹ thuật, Hà Nội 2009 [2] Trần Doãn Tiến. Cơ sở dao động trong kỹ thuật, NXB Đại học và THCN, Hà Nội 1981. [3]Phan Nguyên Di, Nguyễn Văn Khang, Tính toán dao động máy, NXB Khoa học và Kỹ thuật, Hà Nội 1991. [4] Nguyễn Xuân Hùng, Tính toán chính xác kết cấu trên máy tính, NXB Khoa học và Kỹ thuật, Hà Nội 2002. [5] Nguyễn Văn Khang, Cơ sở Cơ học kỹ thuật, Tập I và tập II, NXB Đại học quốc gia, Hà Nội 2003 [6] Lê Quang Minh, Nguyễn Văn Vƣợng, Sức bền vật liệu, NXB Giáo dục, Hà Nội 2004. [7] Lê Ngọc Hồng, Sức bền vật liệu, NXB Khoa học kỹ thuật 2002. [8] Bùi Trọng Lựu, Sức bền vật liệu tập 1, NXB Đại học và Trung học chuyên nghiệp, 2004. [9] Bùi Trọng Lựu, Sức bền vật liệu tập 2, NXB Đại học và Trung học chuyên nghiệp, 2004. [10] Bùi Trọng Lựu, Nguyễn Văn Vƣợng, Bài tập Sức bền vật liệu, NXB Giáo dục 2004. [11] Đỗ Sanh, Nguyễn Văn Khang. Cơ học tập 2. NXB Giáo dục 2004. [12] Nguyễn Văn Khang, Thái Mạnh Cầu, Vũ Văn Khiêm, Nguyễn Nhật Lệ, Bài tập dao động kỹ thuật, NXB Khoa học và Kỹ thuật, Hà Nội 2009. 174
File đính kèm:
 giao_trinh_dao_dong_ky_thuat.pdf
giao_trinh_dao_dong_ky_thuat.pdf

