Estimation of heat transfer parameters by using trained pod - rbf and grey wolf optimizer

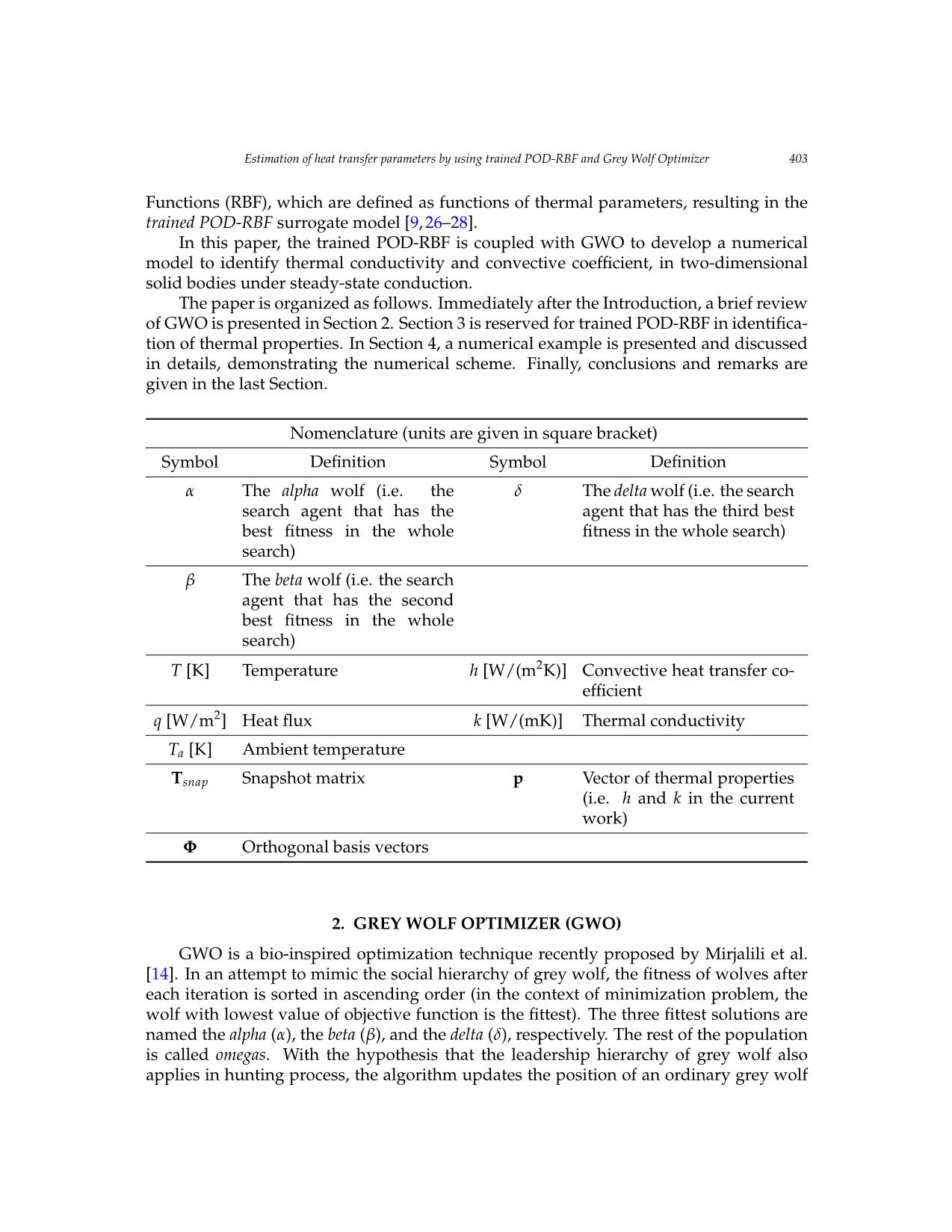
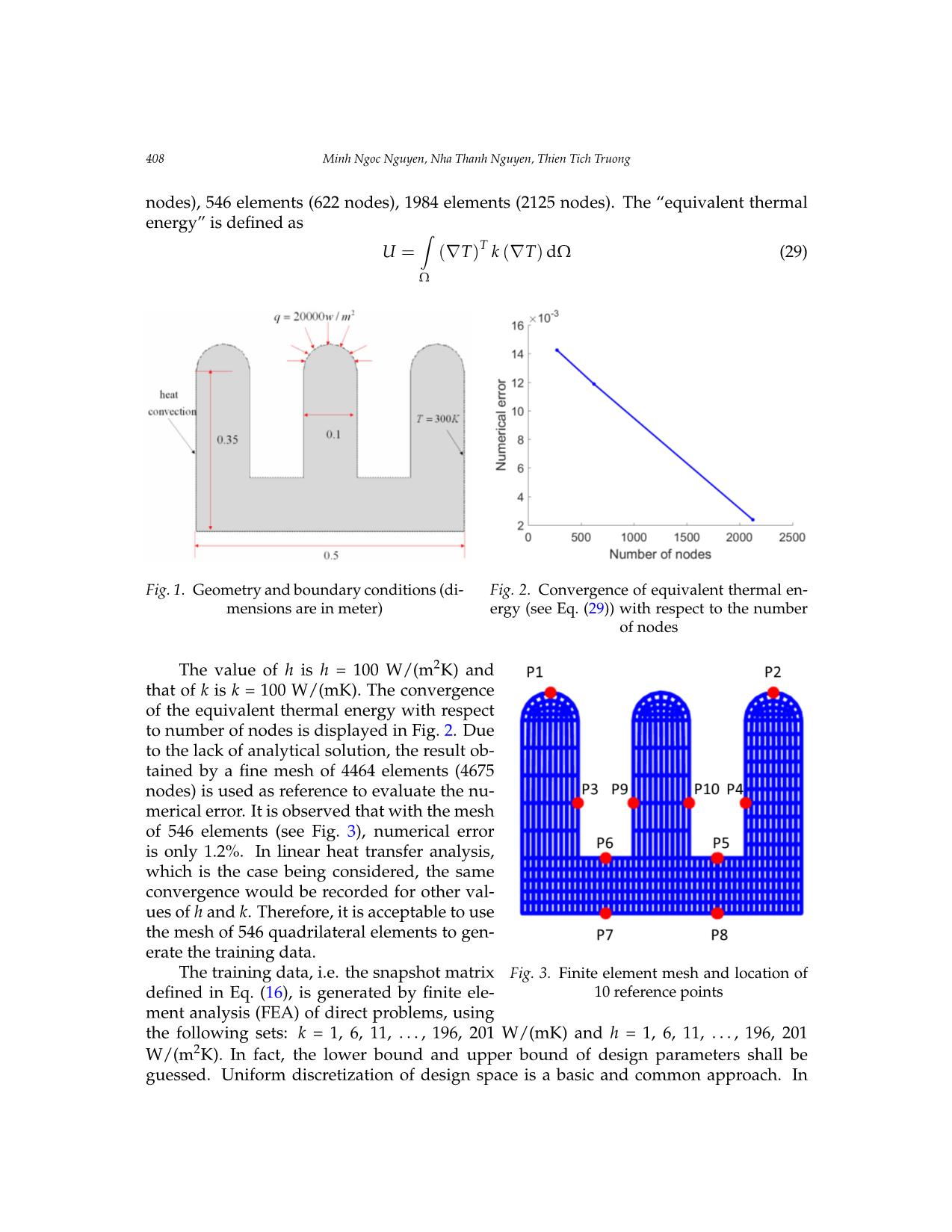
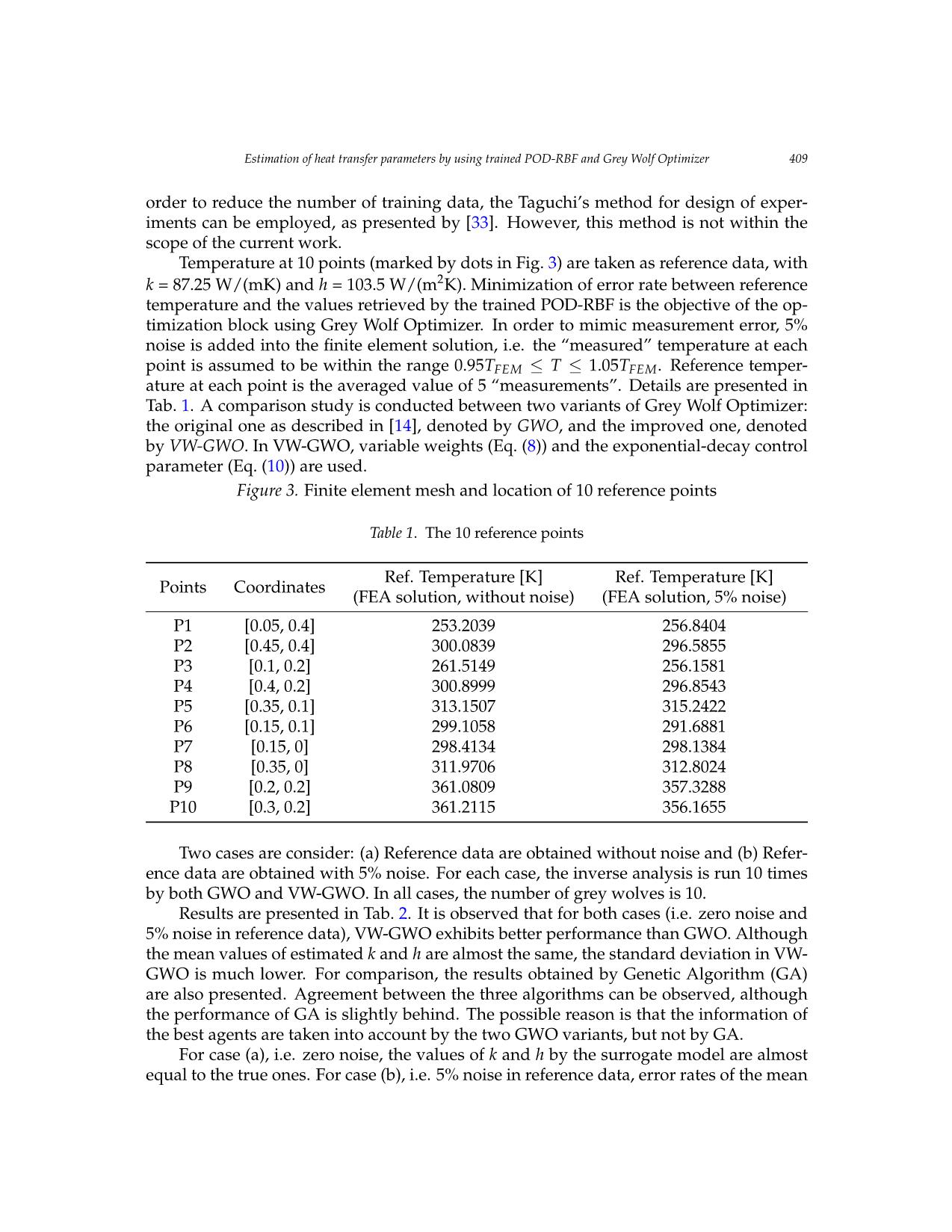
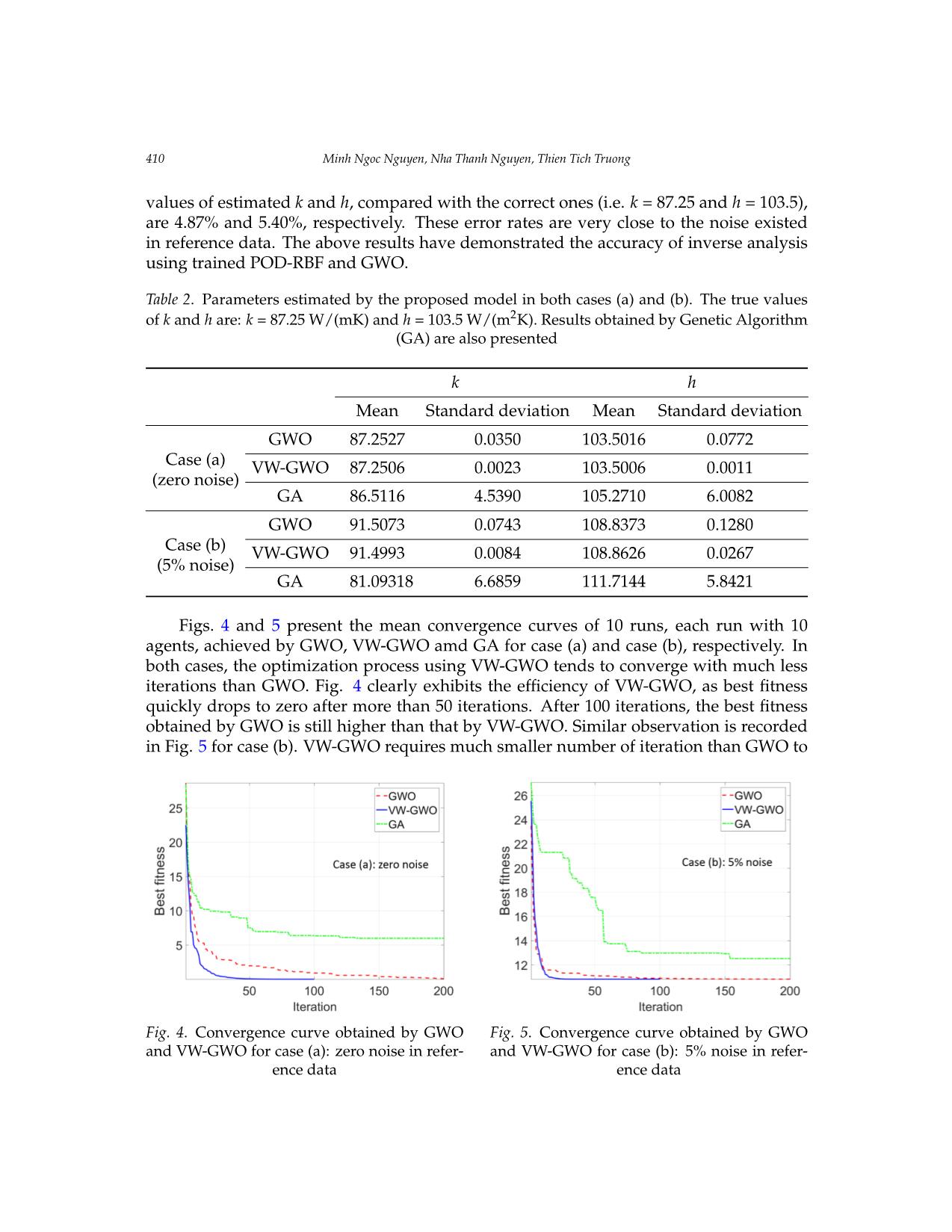
 Vietnam Journal of Mechanics, VAST, Vol.42, No. 4 (2020), pp. 401 – 414
 DOI: https://doi.org/10.15625/0866-7136/15015
 ESTIMATION OF HEAT TRANSFER PARAMETERS BY
 USING TRAINED POD-RBF AND GREY WOLF OPTIMIZER
 Minh Ngoc Nguyen1,2,∗, Nha Thanh Nguyen1,2, Thien Tich Truong1,2
 1Ho Chi Minh City University of Technology, Vietnam
 2Vietnam National University Ho Chi Minh City, Vietnam
 ∗E-mail: nguyenngocminh@hcmut.edu.vn
 Received: 27 April 2020 / Published online: 16 December 2020
 Abstract. The article presents a numerical model for estimation of heat transfer parame-
 ters, e.g. thermal conductivity and convective coefficient, in two-dimensional solid bodies
 under steady-state conduction. This inverse problem is stated as an optimization prob-
 lem, in which input is reference temperature data and the output is the design variables,
 i.e. the thermal properties to be identified. The search for optimum design variables is
 conducted by using a recent heuristic method, namely Grey Wolf Optimizer. During the
 heuristic search, direct heat conduction problem has to be solved several times. The set of
 heat transfer parameters that lead to smallest error rate between computed temperature
 field and reference one is the optimum output of the inverse problem. In order to acceler-
 ate the process, the model order reduction technique Proper-Orthogonal-Decomposition
 (POD) is used. The idea is to express the direct solution (temperature field) as a linear
 combination of orthogonal basis vectors. Practically, a majority of the basis vectors can be
 truncated, without losing much accuracy. The amplitude of this reduced-order approxi-
 mation is then further interpolated by Radial Basis Functions (RBF). The whole scheme,
 named as trained POD-RBF, is then used as a surrogate model to retrieve the heat transfer
 parameters.
 Keywords: inverse analysis, Grey Wolf Optimizer, heat transfer parameters identification,
 Proper Orthogonal Decomposition (POD), Radial Basis Function (RBF).
 1. INTRODUCTION
 In direct heat transfer analysis, distribution of temperature within a conducting do-
main is determined given known boundary conditions and thermal properties. In con-
trast, based on the knowledge of temperature history within a conducting body, inverse
heat transfer analysis is used to determine the thermal properties and/or boundary con-
ditions. The estimated quantities of inverse heat transfer analysis are very sensitive to
the inaccuracy of input data. Mathematically, the problem is ill-posed [1]. Unfortunately,
 © 2020 Vietnam Academy of Science and Technology
402 Minh Ngoc Nguyen, Nha Thanh Nguyen, Thien Tich Truong
noise in measurement of temperature is not avoidable. Therefore, development of com-
putational schemes which can overcome the issue of ill-posedness has attracted much
attention from researchers.
 Inverse analysis has been widely used in heat transfer to identify heat flux [2–4],
boundary conditions [5–7] and unknown thermal properties such as conductivity and
convective coefficient [8–11]. Basically, the problem is described as minimization of the
error rate between computed temperature and measured data. The design variables are
the unknown quantities to be determined. For solution of optimization problem, ei-
ther gradient-based or non-gradient-based methods can be used. The gradient-based
approaches [3,4,8] usually involve sensitivity analysis, i.e. the computation of derivative
of objective function with respect to the sought variables. However, derivation of objec-
tive function as an explicit function of design variables is usually not a trivial task. An-
other drawback is that the gradient-based approach may fall into local optimum. On the
other hand, the non-gradient-based methods do not require sensitivity analysis. Instead,
various heuristic algorithms are used such as Genetic Algorithm [11], Particle Swarm
Optimization [2], Differential Evolution [12], Firefly Algorithm [7], Cuckoo Search [13]
and so on. Although each algorithm has a different strategy, they commonly employ
a group of M agents which search N rounds in the admissible solution space to find
the optimum one, i.e. the unknown quantities to be estimated. Indeed, it is common
knowledge that there exists no algorithm which is superior to the others in all types of
problems. Nevertheless, the attractiveness of GWO algorithm comes from the fact that it
has small number of user-defined parameters to control the balance of exploitation (local
search) and exploration (global search). In this work, the recently proposed Grey Wolf
Optimizer (GWO) [14] is used to solve the optimization problem to identify the thermal
parameters, e.g. heat conductivity and convective coefficient. The algorithm has been
widely applied in many fields such as machine learning [15,16], electric engineering [17],
earthquake engineering [18], image processing [19], path planning [20]. However, to the
best knowl ... oise. 
 Comparison between two variants of Grey Wolf Optimizer, i.e. the original one (namely GWO) 
 and the improved one (namely VW-GWO) has been conducted. It is shown that by using VW-GWO, 
 Figure 5. Convergence curve obtained by GWO and VW-GWO for case (b): 5% noise in reference data 
 5. CONCLUSION AND OUTLOOKS 
 In this paper, a trained POD-RBF system is coupled with Grey Wolf Optimizer to develop a 
surrogate model for estimation of thermal parameters. It is demonstrated that the proposed numerical 
scheme yields reliable output. When there is no noise in reference data, the error rate between predicted 
thermal parameters and the true ones is almost zero. When noise is included in the reference data, the 
parameters are predicted with an error rate within the range of noise. 
 Comparison between two variants of Grey Wolf Optimizer, i.e. the original one (namely GWO) 
and the improved one (namely VW-GWO) has been conducted. It is shown that by using VW-GWO, 
 Estimation of heat transfer parameters by using trained POD-RBF and Grey Wolf Optimizer 411
reach convergence. Computational time for each iteration is not much difference between
GWO and VW-GWO. Therefore, with higher rate of convergence, there is potential to
save elapsed time by using VW-GWO. The number of necessary iterations is not known
beforehand. It is possible to define a lower limit for the number of iterations. After that
limit, if fitness value (i.e. the value of objective function) repeatedly does not change
within many iterations (e.g. 50 iterations), the optimization process can be considered as
being converged and thus can be terminated.
 5. CONCLUSION AND OUTLOOKS
 In this paper, a trained POD-RBF system is coupled with Grey Wolf Optimizer to de-
velop a surrogate model for estimation of thermal parameters. It is demonstrated that the
proposed numerical scheme yields reliable output. When there is no noise in reference
data, the error rate between predicted thermal parameters and the true ones is almost
zero. When noise is included in the reference data, the parameters are predicted with an
error rate within the range of noise.
 Comparison between two variants of Grey Wolf Optimizer, i.e. the original one
(namely GWO) and the improved one (namely VW-GWO) has been conducted. It is
shown that by using VW-GWO, the convergence rate of the optimizing process is in-
creased. Therefore, less number of iterations is required and as a result, computational
time can be potentially saved.
 There are still many issues left open. Improving computational efficiency of the opti-
mization process is a constant demand. For the POD-RBF block, the size of training data
would increase with respect to the number of the parameters to be identified. Loosely
speaking, if identification of 1 parameter needs N samples, then identification of d pa-
rameters would need Nd samples. Special technique is necessary to handle with a large
and multi-dimensional data. Experiments could be involved in both the preparation of
training data and the collection of reference data. However, a large number of data is
usually required for training. Therefore, a numerical data generator might be more prac-
tical. On the other hand, the numerical model has to be verified before it can be used for
generation of training data. The reference data in practice shall be obtained from mea-
surement. Obviously, the more number of sensors are placed, the more information could
be gained. Unfortunately, in most of the cases, the number of sensors cannot be large due
to the cost issues. Therefore, it is necessary to optimize the number of sensors and the
positions where the sensors are located [34, 35]. This is also an interesting research topic
which can be employed together with inverse analysis.
 ACKNOWLEDGMENT
 We acknowledge the support of time and facilities from Ho Chi Minh City University
of Technology (HCMUT), VNU-HCM for this study.
 REFERENCES
 [1] M. N. Ozisik¨ and H. R. B. Orlande. Inverse heat transfer: fundamentals and applications. Taylor
 & Francis, (2000).
412 Minh Ngoc Nguyen, Nha Thanh Nguyen, Thien Tich Truong
 [2] F. B. Liu. Inverse estimation of wall heat flux by using particle swarm optimization algo-
 rithm with Gaussian mutation. International Journal of Thermal Sciences, 54, (2012), pp. 62–69.
 https://doi.org/10.1016/j.ijthermalsci.2011.11.013.
 [3] H. L. Lee, W. J. Chang, W. L. Chen, and Y. C. Yang. Inverse heat transfer anal-
 ysis of a functionally graded fin to estimate time-dependent base heat flux and
 temperature distributions. Energy Conversion and Management, 57, (2012), pp. 1–7.
 https://doi.org/10.1016/j.enconman.2011.12.002.
 [4] F. Mohebbi, B. Evans, A. Shaw, and M. Sellier. An inverse analysis for determination of space-
 dependent heat flux in heat conduction problems in the presence of variable thermal conduc-
 tivity. International Journal for Computational Methods in Engineering Science and Mechanics, 20,
 (3), (2019), pp. 229–241. https://doi.org/10.1080/15502287.2019.1615579.
 [5] A. E. Segall, D. Engels, and C. Drapaca. Inverse determination of thermal
 boundary conditions from transient surface temperatures and strains in slabs
 and tubes. Materials and Manufacturing Processes, 27, (8), (2012), pp. 860–868.
 https://doi.org/10.1080/10426914.2012.663130.
 [6] M. Ebrahimian, R. Pourgholi, M. Emamjome, and P. Reihani. A numerical solution of an in-
 verse parabolic problem with unknown boundary conditions. Applied Mathematics and Com-
 putation, 189, (1), (2007), pp. 228–234. https://doi.org/10.1016/j.amc.2006.11.062.
 [7] H. L. Zhou, X. H. Zhao, B. Yu, H. L. Chen, and Z. Meng. Firefly algorithm com-
 bined with Newton method to identify boundary conditions for transient heat conduc-
 tion problems. Numerical Heat Transfer, Part B: Fundamentals, 71, (3), (2017), pp. 253–269.
 https://doi.org/10.1080/10407790.2016.1277915.
 [8] F. Mohebbi and M. Sellier. Estimation of thermal conductivity, heat transfer coefficient, and
 heat flux using a three dimensional inverse analysis. International Journal of Thermal Sciences,
 99, (2016), pp. 258–270. https://doi.org/10.1016/j.ijthermalsci.2015.09.002.
 [9] Z. Ostrowski, R. Białecki, and A. J. Kassab. Solving inverse heat conduction problems using
 trained POD-RBF network inverse method. Inverse Problems in Science and Engineering, 16,
 (1), (2008), pp. 39–54. https://doi.org/10.1080/17415970701198290.
[10] C. Y. Yang. Estimation of the temperature-dependent thermal conductivity in inverse
 heat conduction problems. Applied Mathematical Modelling, 23, (6), (1999), pp. 469–478.
 https://doi.org/10.1016/s0307-904x(98)10093-8.
[11] R. Pourgholi, H. Dana, and S. H. Tabasi. Solving an inverse heat conduction problem using
 genetic algorithm: sequential and multi-core parallelization approach. Applied Mathematical
 Modelling, 38, (7-8), (2014), pp. 1948–1958. https://doi.org/10.1016/j.apm.2013.10.019.
[12] R. Das and B. Kundu. Direct and inverse approaches for analysis and optimization of fins
 under sensible and latent heat load. International Journal of Heat and Mass Transfer, 124, (2018),
 pp. 331–343. https://doi.org/10.1016/j.ijheatmasstransfer.2018.03.059.
[13] H.-L. Chen, B. Yu, H. L. Zhou, and Z. Meng. Improved cuckoo search algorithm for solv-
 ing inverse geometry heat conduction problems. Heat Transfer Engineering, 40, (3-4), (2019),
 pp. 362–374. https://doi.org/10.1080/01457632.2018.1429060.
[14] S. Mirjalili, S. M. Mirjalili, and A. Lewis. Grey wolf optimizer. Advances in Engineering Soft-
 ware, 69, (2014), pp. 46–61. https://doi.org/10.1016/j.advengsoft.2013.12.007.
[15] E. Emary, H. M. Zawbaa, and A. E. Hassanien. Binary grey wolf optimiza-
 tion approaches for feature selection. Neurocomputing, 172, (2016), pp. 371–381.
 https://doi.org/10.1016/j.neucom.2015.06.083.
 Estimation of heat transfer parameters by using trained POD-RBF and Grey Wolf Optimizer 413
[16] S. Eswaramoorthy, N. Sivakumaran, and S. Sekaran. Grey wolf optimization based
 parameter selection for support vector machines. COMPEL-The International Jour-
 nal for Computation and Mathematics in Electrical and Electronic Engineering, (2016).
 https://doi.org/10.1108/compel-09-2015-0337.
[17] A. Lakum and V. Mahajan. Optimal placement and sizing of multiple active power
 filters in radial distribution system using grey wolf optimizer in presence of nonlin-
 ear distributed generation. Electric Power Systems Research, 173, (2019), pp. 281–290.
 https://doi.org/10.1016/j.epsr.2019.04.001.
[18] X. Song, L. Tang, S. Zhao, X. Zhang, L. Li, J. Huang, and W. Cai. Grey wolf optimizer for
 parameter estimation in surface waves. Soil Dynamics and Earthquake Engineering, 75, (2015),
 pp. 147–157. https://doi.org/10.1016/j.soildyn.2015.04.004.
[19] S. Zhang and Y. Zhou. Template matching using grey wolf optimizer with lateral inhibition.
 Optik, 130, (2017), pp. 1229–1243. https://doi.org/10.1016/j.ijleo.2016.11.173.
[20] S. Zhang, Y. Zhou, Z. Li, and W. Pan. Grey wolf optimizer for unmanned combat
 aerial vehicle path planning. Advances in Engineering Software, 99, (2016), pp. 121–136.
 https://doi.org/10.1016/j.advengsoft.2016.05.015.
[21] R. A. Białecki, A. J. Kassab, and A. Fic. Proper orthogonal decomposition and modal analysis
 for acceleration of transient FEM thermal analysis. International Journal for Numerical Methods
 in Engineering, 62, (6), (2005), pp. 774–797. https://doi.org/10.1002/nme.1205.
[22] A. Fic, R. A. Białecki, and A. J. Kassab. Solving transient nonlinear heat con-
 duction problems by proper orthogonal decomposition and the finite-element
 method. Numerical Heat Transfer, Part B: Fundamentals, 48, (2), (2005), pp. 103–124.
 https://doi.org/10.1080/10407790590935920.
[23] X. Zhang and H. Xiang. A fast meshless method based on proper orthogonal decomposition
 for the transient heat conduction problems. International Journal of Heat and Mass Transfer, 84,
 (2015), pp. 729–739. https://doi.org/10.1016/j.ijheatmasstransfer.2015.01.008.
[24] N. N. Minh, N. T. Nha, T. T. Thien, and B. Q. Tinh. Efficient numerical analy-
 sis of transient heat transfer by Consecutive-Interpolation and Proper Orthogonal De-
 composition. Science and Technology Development Journal, 20, (K9), (2017), pp. 5–14.
 https://doi.org/10.32508/stdj.v20ik9.1671.
[25] Z. Ostrowski, R. A. Białecki, and A. J. Kassab. Estimation of constant thermal conductivity by
 use of proper orthogonal decomposition. Computational Mechanics, 37, (1), (2005), pp. 52–59.
 https://doi.org/10.1007/s00466-005-0697-y.
[26] C. A. Rogers, A. J. Kassab, E. A. Divo, Z. Ostrowski, and R. A. Bialecki. An inverse POD-
 RBF network approach to parameter estimation in mechanics. Inverse Problems in Science and
 Engineering, 20, (5), (2012), pp. 749–767. https://doi.org/10.1080/17415977.2012.693080.
[27] M. Bocciarelli, V. Buljak, C. K. S. Moy, S. P. Ringer, and G. Ranzi. An inverse
 analysis approach based on a POD direct model for the mechanical characteriza-
 tion of metallic materials. Computational Materials Science, 95, (2014), pp. 302–308.
 https://doi.org/10.1016/j.commatsci.2014.07.025.
[28] S. Khatir and M. A. Wahab. Fast simulations for solving fracture mechanics inverse prob-
 lems using POD-RBF XIGA and Jaya algorithm. Engineering Fracture Mechanics, 205, (2019),
 pp. 285–300. https://doi.org/10.1016/j.engfracmech.2018.09.032.
[29] Z. M. Gao and J. Zhao. An improved grey wolf optimization algorithm
 with variable weights. Computational Intelligence and Neuroscience, 2019, (2019).
 https://doi.org/10.1155/2019/2981282.
414 Minh Ngoc Nguyen, Nha Thanh Nguyen, Thien Tich Truong
[30] A. Chatterjee. An introduction to the proper orthogonal decomposition. Current Science,
 (2000), pp. 808–817.
[31] G. R. Liu. Meshfree methods: moving beyond the finite element method. Taylor & Francis, second
 edition, (2010).
[32] C. H. Thai, V. N. V. Do, and H. Nguyen-Xuan. An improved Moving Kriging-based mesh-
 free method for static, dynamic and buckling analyses of functionally graded isotropic
 and sandwichESTIMATION plates. OF HEATEngineering TRANSFER Analysis PARAMETERS with BoundaryBY INVERSE Elements ANALYSIS, 64USING, (2016), 11 pp. 122–136.
 https://doi.org/10.1016/j.enganabound.2015.12.003TRAINED POD-RBF .
[33] S.the U. converge Hamimnce rate and of the R. optimizing P. Singh. process Taguchi-based is increased. Therefore, design less number of experiments of iterations is in train-
 ingrequired POD-RBF and as a result surrogate, computational model time can for be inversepotentially saved. material modelling using nanoinden-
 tation. ThereInverse are still Problems many issues in left Science open. Improving and Engineering computational, efficiency25, (3), of the (2017), optimization pp. 363–381.
 https://doi.org/10.1080/17415977.2016.1161036process is a constant demand. For the POD-RBF block, the. size of training data would increase with 
[34] C.respect Leyder, to the V. number Dertimanis, of the parameters A. Frangi, to be identified E. Chatzi,. Loosely andspeaking, G. if Lombaert. identification of Optimal 1 sen-
 sorparameter placement needs N methods samples, then and identification metrics–comparison of d parameters would and implementationneed Nd samples. Special on a timber
 technique is necessary to handle with a large and multi-dimensional data. Experiments could be involved 
 framein both structure. the preparationStructure of training anddata and Infrastructure the collection of Engineering reference data., However,14, (7), a large (2018), number pp. of 997–1010.
 https://doi.org/10.1080/15732479.2018.1438483data is usually required for training. Therefore, a numerical. data generator might be more practical. On 
[35] D.the Dinh-Cong, other hand, the H. numerical Dang-Trung, model has and to be T. verified Nguyen-Thoi. before it can An be efficientused for generation approach of training for optimal sen-
 sordata. placement The reference and data damage in practice identification shall be obtained in from laminated measurement. composite Obviously, structures. the more numberAdvances in En-
 gineeringof sensors Software are placed, the more information could be gained. Unfortunately, in most of the cases, the 
 number of sensors ,cannot119, (2018),be large pp.due to 48–59. the cost https://doi.org/10.1016/j.advengsoft.2018.02.005 issues. Therefore, it is necessary to optimize the .
 number of sensors and the positions where the sensors are located [34, 35]. This is also an interesting 
 research topic which can be employed togetherAPPENDIX with inverse analysis. A 
 The flow chart of the proposed procedure for inverse heat transfer analysis is given
in Fig. A.1. APPENDIX 
 The flow chart of the proposed procedure for inverse heat transfer analysis is given in Figure 6. 
 Figure 6. Flow chart 
 Fig. A.1. Flow chart