Effective medium approximation for conductivity of coated-Inclusion composites with anisotropic coating

 Vietnam Journal of Mechanics, VAST, Vol.41, No. 3 (2019), pp. 233 – 241
 DOI: https://doi.org/10.15625/0866-7136/13717
 EFFECTIVE MEDIUM APPROXIMATION FOR
 CONDUCTIVITY OF COATED-INCLUSION COMPOSITES
 WITH ANISOTROPIC COATING
 Tran Bao Viet1,∗, Nguyen Thi Huong Giang1, Pham Duc Chinh 3
 1University of Transport and Communications, Hanoi, Vietnam
 2Institute of Mechanics, VAST, Hanoi, Viet Nam
 ∗E-mail: viettb@utc.edu.vn
 Received: 30 March 2019 / Published online: 24 June 2019
 Abstract. Effective medium approximations are constructed in this paper to estimate the
 macroscopic conductivity of coated-inclusion composites with thin anisotropic coating.
 The two-phase coated-inclusion are substituted by equivalent one-phase inclusion, using
 the multi-coated spheres assemblage and the differential substitution approaches. Then,
 the usual effective medium approximation schemes are applied to the equivalent medium
 to estimate the conductivity of original three-phase composites. The results obtained were
 compared with the numerical simulation by finite element method in 2D show the effec-
 tiveness of the methods.
 Keywords: coated-inclusion; effective conductivity; equivalent-inclusion approach;
 anisotropic coating.
 1. INTRODUCTION
 A widely recognized observation is that the effective behavior of a matrix-inclusion
composites depends on the coating shells (interface or chemical reaction layer). Over sev-
eral decades, determining the thermal gradient and flux fields in the layers has become a
interesting subject for numerous theoretical [1–9].
 Simple analytical approaches are developed recently by us to estimate macroscopic
properties of coated-inclusion composites [10–14]. However, these studies only men-
tioned the case of isotropic coating. This paper is concerned with the determination of
the effective conductivity of coated-inclusion composite with thin anisotropic coating by
simple analytical approach. The two-phase coated-inclusion is substituted by equiva-
lent one-phase inclusion, using the multi-coated spheres assemblage and the differential
substitution approaches. Then, the usual effective medium approximation schemes are
applied to the equivalent medium to estimate the conductivity of original three-phase
composites. The results obtained were compared with the numerical simulation by finite
element method in 2D to show the effectiveness of the methods.
 
c 2019 Vietnam Academy of Science and Technology
234 Tran Bao Viet, Nguyen Thi Huong Giang, Pham Duc Chinh
 2. THEORETICAL HOMOGENIZATION FRAMEWORK
2.1. The sphere assemblage model of two phase material
 We start with a particularly simple situation where the two component d-dimensional
composite is a suspension of random spherical/circular inclusions of conductivity c1 and
volume proportion v1 in a continuous matrix of conductivity cM and volume fraction
vM. The main idea of the sphere assemblage model of two phase matrix-based material
is that we consider a spherical/circular inclusion surrounded by a coated spherical/cir-
cular matrix shell embedded in an effective equivalent infinite medium (Fig.1). The
effective conductivity of the composite is calculated based on the Hashin-Strickman two-
phase coated spheres assemblage and Hill substitution scheme [15]
 −1
 e f f  v1 vM 
 c = P(v1, c1, cM) = + − (d − 1)cM. (1)
 c1 + (d − 1)cM dcM
 Effective
 medium
 Inclusion
 =
 Matrix
 Fig. 1. the sphere assemblage model of two phase material
 Two consequences of (1) corresponding respectively with the case of v1 → 0 and the
opposite case of vM → 0 are respectively
 e f f (c1 − cM)dcM 2
 c = cM + v1 + O(v1), (2)
 c1 + (d − 1)cM
and
 e f f (cM − c1)[c1 + (d − 1)cM] 2
 c = c1 + vM + O(vM). (3)
 dcM
 It is necessary to note that Eq. (2) are the theoretical dilute solution results for the
inhomogeneities suspended in an infinite matrix while Eq. (3) present the effective con-
ductivity of the suspension of thin coating inclusion that is used below for further calcula-
tions in this paper. The two effective conductivities from (2, 3) obey the Hashin-Shtrikman
 Effective medium approximation for conductivity of coated-inclusion composites with anisotropic coating 235
bounds which are the best mathematical bounds based on the component properties and
volume content of d-dimensional composites,
 e f f
 HSL = P(cmin) ≤ c ≤ P(cmax) = HSU, (4)
with
 cmin = min{cM, c1}, cmax = max{cM, c1}, (5)
and
  −1
 vM v1
 P(c) = + − c∗, c∗ = (d − 1)c1. (6)
 cM + c∗ c1 + c∗
2.2. Differential substitution construction
 Now we consider a more complex situation where the inclusion characterizing by
c1, v1 surrounded by a thing coating shell of conductivity cc and volume fraction vc. To
account for the thin coating effect, we base on the differential scheme construction pro-
cess proposed recently in Pham et al. [16]. In which, Pham consider that the thin coating
shell is divided into some infini ... ). By combining Eq. (3) and the differ-
ential substitution procedure (in a similar way as the classical differential scheme), the
equivalent conductivity of the thin coated inclusion can be obtained from the differential
equation
 dc 1 (cc − c)[c + (d − 1)cc] 1c
 = , c(v = 0) = c1, c = c(v = vc). (7)
 dv 1 − v dcc
 Then we replace the inclusion (c1, v1) by the coated inclusion having the effective
 1c
conductivity c and volume proportion v1c in Eqs. (1)–(3), we obtain the respective ef-
fective conductivity formulas of the matrix-based composite materials with coated inclu-
sions.
 3. THIN ANISOTROPIC COATINGS WITH RADIALLY VARIABLE
 CONDUCTIVITIES AND EQUIVALENT INCLUSION APPROACH
 In the section, we are interested in constructing a simple approximation to take into
account the effect of thin anisotropic coatings on the effective conductivity of the suspen-
sion of the coated inclusions in the matrix. To do this, the composite material is composed
of the spherical inclusions V1 of radius R1, volume proportion v1, and isotropic conduc-
tivity c1, is coated by the spherical shell Vc \ V1 of outer radius Rc volume proportion
vc, and anisotropic conductivity, with the normal (in the radial direction) conductivity
cN and transverse (in the coating surface directions) conductivity cT. The coated sphere
then is embedded in the matrix shell VM \ V1 of outer radius RM, volume proportion vM,
and isotropic conductivity cM. The anisotropic shell can be equivalently presented as be-
 h R − R
ing composed of 2m ultra-thin spherical shell coatings of thickness = c 1 , and
 2m 2m
236 Tran Bao Viet, Nguyen Thi Huong Giang, Pham Duc Chinh
isotropic conductivities c2 and c3, alternately, in the limit m → ∞, with
 1
 c = (c + c ) , c = 2(c−1 + c−1)−1 , (8)
 T 2 2 3 N 2 3
while
 v2 = v3 = vc/2 . (9)
 Following the mathematical developments presented above, we have a asymptotic
expression
 1c ∆v  (c2 − c1)[c1 + (d − 1)c2] (c3 − c1)[c3 + (d − 1)c1]  2
 c = c1 + m + m + O(cc )
 2m dc2 dc3
 ∆v 2
 = c1 + (cI − c1)(c1 + cII ) + O(cc ), (10)
 dcN
where
 1
 c = {[(d − 2)2c2 + 4(d − 1)c c ]1/2 − (d − 2)c } ,
 I 2 N T N N
 1
 c = {[(d − 2)2c2 + 4(d − 1)c c ]1/2 + (d − 2)c } . (11)
 II 2 N T N N
 Letting m → ∞, we obtain the ordinary differential equation determining the effec-
tive conductivity of the assemblage of coated inclusions, with inclusions having conduc-
tivity c1, volume proportion v1, and anisotropic coating of variable conductivities cN(v),
cT(v), volume proportion vc
 dc 1 (cI − c)(c + cII ) e f f
 = , c(0) = c1, c = c(vc). (12)
 dv 1 − v dcN
 In the case cN = const, cT = const, Eq. (12) can be integrated explicitly
 dcN
 cI +cII
 1c eq cII (c1 − cI ) + cI (c1 + cII )v˜1 v1 eq
 c = c = , v˜1 = , v = v1 + vc . (13)
 dcN v + v
 cI +cII 1 c
 cI − c1 + (c1 + cII )v˜1
 From the formula (13) for the effective conductivity of the assemblage of coated in-
clusions with inclusions having anisotropic coating of variable conductivities, we pro-
pose a hypothesis that the real coated inclusion is replaced by a fictive equivalent and
 eq eq
homogeneous inclusion with the volume factor noted by v = v1 + vc and c having the
value from the formula (15). One the coated inclusion is replaced by the homogeneous
inclusion, the effective conductivity of the original material can be obtained by the clas-
sical effective medium approximations. According to (1), the coated inclusion composite
has the effective conductivity
 eq −1
 e f f  v vM 
 c = eq + − (d − 1)cM . (14)
 c + (d − 1)cM dcM
 In the general situation where the material is composed of the matrix and the dif-
ferent type of inclusions with anisotropic coating layer, the equivalent strategy is taken
 Effective medium approximation for conductivity of coated-inclusion composites with anisotropic coating 237
into account for all different type of inclusions then we have a multicomponent compos-
ite material with different type of equivalent inclusions having conductivity ceq1, volume
fraction veq1; conductivity ceq2, volume fraction veq2;...; ceqβ, volume fraction veqβ in a
 eqβ
matrix of conductivity cM, volume fraction vM. It necessary to note that c can be also
calculated by (13). Then the effective conductivity of the multicomponent matrix-based
composite can be determined by applying the simple polarization approximation [14]
 !−1
 veqβ v
 e f f = + M − ( − )
 c ∑ eqβ d 1 cM. (15)
 β c + (d − 1)cM dcM
 4. NUMERICAL SIMULATIONS AND APPLICATIONS
 In order to verify the above result, we make finite element calculations for a number
of periodic suspensions of circles in two dimensions. Due to the periodicity condition of
the microscopic heat flux field q(z), the average of the microscopic heat flux fields q(z)
over the domain of periodic cell U and the Representative Volume Element V are equal.
This indicates that the macroscopic relationships can be determined numerically from
the solution over the finite domain U. Some details concerning the global temperature
field equations, the boundary conditions, the open source finite element code used . . . are
identical than the ones presented in works of Tran et al. [14], and no need to rewrite in this
text. The improvement of numerical simulation in this paper come from the anisotropic
properties of the coating shell. In which, two types of rectangular unit cell are accounted
for calculation (square and hexagonal arrays of coated circles where their lengths are de-
noted by a1 and a2 - see Fig.2). To model anisotropic coatings with radially variable
conductivities cN and cT, we divide the coated shell into some parts of same size, shape
and different direction characterizing by angular β and α (Fig.3). For each part (char-
acterizing by α and β), conductivities are fixed at c (c11, c22, c21) in the global coordinate
 0 0
(x1, x2) depend on cN, cT and position point that define by local coordinate (x1, x2) (Fig.3)
 a2 = a1/ 3
 a2 = a1
 1/2 a1
 1/2 a1
 (a) (b)
 Fig. 2. Periodic cell: (a) - square array; (b) - hexagonal array
238 Tran Bao Viet, Nguyen Thi Huong Giang, Pham Duc Chinh
by the relationships
 2 2
 c11 = cN cos α + cT sin α, (16)
 2 2
 c22 = cN sin α + cT cos α, (17)
 c21 = (cN − cT) cos α sin α. (18)
 3.50
 3.48
 x
 2 3.46
 3.44
 x’1
 eff 3.42
 C
 3.40
x’
 2 3.38
 b
 3.36
 a
 3.34
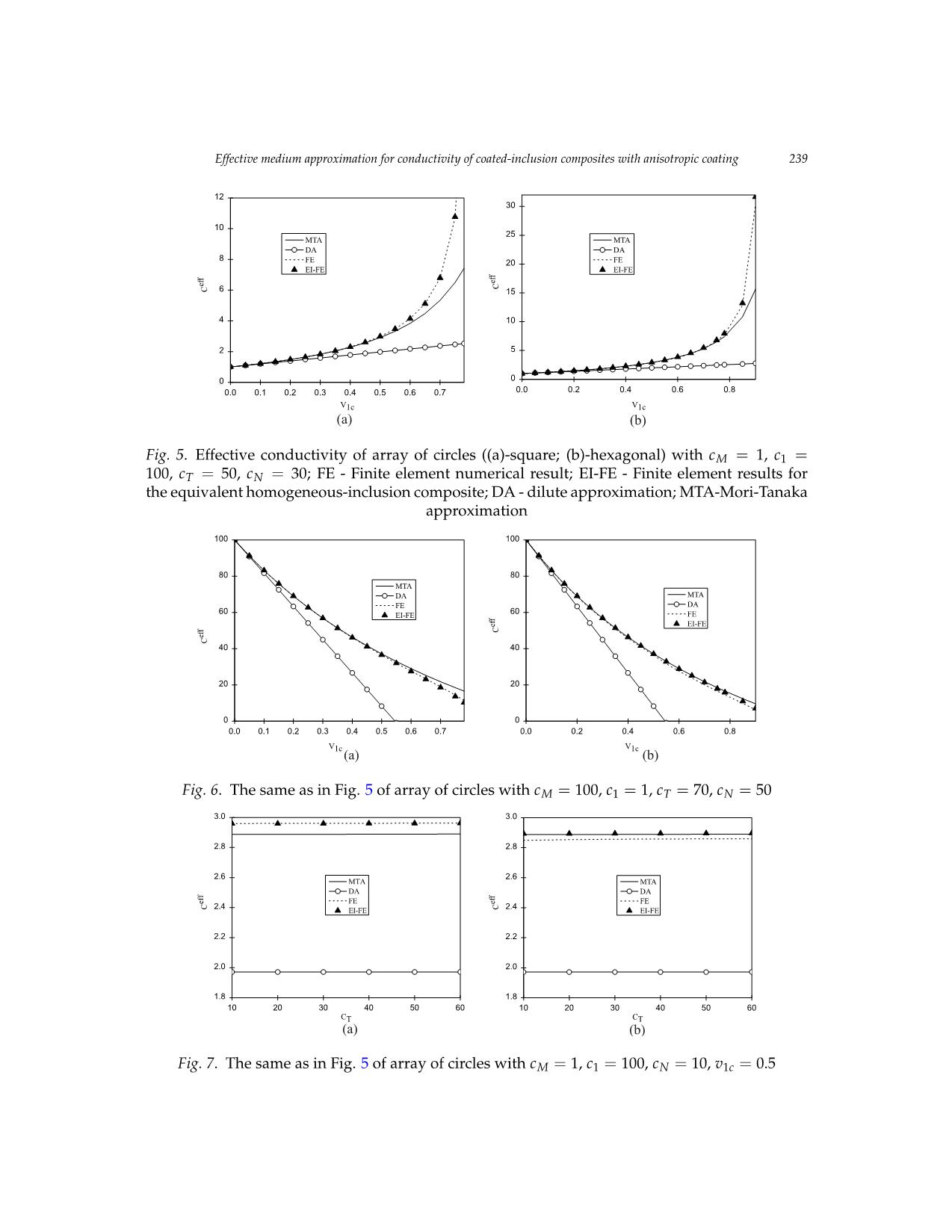
 1 10 100
 x1 b
Fig. 3. Rotational coordinate transforma- Fig. 4. Angular convergence test
 tion
 In fact, the angle β need enough small to guarantee the homogeneous properties of
materials. A Finite element method convergence test between angular value and effective
conductivity are presented in Fig.4 with cM = 1, c1 = 100, cT = 50, cN = 30, v1 = 10vc,
 eq o
v1c = v = 0.5. From this test, we adopt a value of β = 3 for the further numerical
calculations.
 For particular calculations, we take cM = 1, c1 = 100, cT = 50, cN = 30 (and
 eq
cM = 100, c1 = 1, cT = 70, cN = 50), v1 = 10vc, v1c = v = v1 + vc = 0 → 0.78 for
square array of coated circles and v1c = v1 + vc = 0 → 0.905 for the hexagonal array. The
curves in Figs.5 and6 show that the numerical calculations for both equivalent and orig-
inal medium are close for all the ranges of parameters up to the maximal packing of the
circles, even though the component properties differ largely. In Figs.5 and6, the Mori-
Tanaka approximation that coincide with Hashin-Shtrikman bounds and the polarization
approximation (14), the dilute approximation for the equivalent homogeneous-inclusion
composite (2) are also compared.
 In next examples, we account for the influence of the ratio cT/cN (1 → 6) to the
effective conductivity of the suspension. The composite is composed of a continuous
matrix with cM = 1, and by coated anisotropic circular inclusions with c1 = 100, cN = 10.
We fix also v1 = 10vc and v1c = 0.5. Numerical configurations considered are square and
hexagonal array of coated circles and equivalent homogeneous circles. Fig.7 presents
respectively some numerical results and analytical estimates for square and hexagonal
arrays. Fig.8 is the same as in Fig.7 with cM = 100, c1 = 1. In these situations, the
Mori-Tanaka approximation (14) appears good regarding its simplicity and generality.
 Effective medium approximation for conductivity of coated-inclusion composites with anisotropic coating 239
 12
 30
 10
 25
 MTA MTA
 DA DA
 8
 FE 20 FE
 EI-FE EI-FE
 eff
 eff
 C
 C 6 15
 4 10
 2 5
 0 0
 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.0 0.2 0.4 0.6 0.8
 V1c V1c
 (a) (b)
Fig. 5. Effective conductivity of array of circles ((a)-square; (b)-hexagonal) with cM = 1, c1 =
100, cT = 50, cN = 30; FE - Finite element numerical result; EI-FE - Finite element results for
the equivalent homogeneous-inclusion composite; DA - dilute approximation; MTA-Mori-Tanaka
 approximation
 100 100
 80 80
 MTA
 DA MTA
 FE DA
 60 EI-FE 60 FE
 eff EI-FE
 C
 eff
 C 40 40
 20 20
 0 0
 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.0 0.2 0.4 0.6 0.8
 V V
 1c (a) 1c (b)
 Fig. 6. The same as in Fig.5 of array of circles with cM = 100, c1 = 1, cT = 70, cN = 50
 3.0
 2.8
 2.6
 MTA
 DA
 eff FE
 C 2.4
 EI-FE
 2.2
 2.0
 1.8
 10 20 30 40 50 60
 CT
 (a) (b)
 Fig. 7. The same as in Fig.5 of array of circles with cM = 1, c1 = 100, cN = 10, v1c = 0.5
240 Tran Bao Viet, Nguyen Thi Huong Giang, Pham Duc Chinh
 36 36
 30 30
 MTA MTA
 24 24
 DA DA
 eff
 eff FE FE
 C
 C EI-FE EI-FE
 18 18
 12 12
 6 6
 10 20 30 40 50 60 10 20 30 40 50 60
 CT CT
 (a) (b)
 Fig. 8. The same as in Fig.5 of array of circles with cM = 100, c1 = 1, cN = 10, v1c = 0.5
 5. CONCLUSIONS
 Based on the multi-coated spheres assemblage and the differential substitution ap-
proaches at dilute configuration, the two-phase coated-inclusion with thin anisotropic
coating are substituted by equivalent one-phase inclusion. Then, the polarization approx-
imation that coincide with well-know Mori-Tanaka approximation in the case of coated
circle inclusions are applied to determine the the conductivity of original composites.
The results obtained were compared with the numerical simulation by finite element
method in 2D. The comparison has shown the effectiveness of the methods. This strat-
egy presented in the paper is a novel and simple method to account the influence of the
anisotrop coating to the global conductivity of multicomponent matrix-based composite
material.
 Developments of the approximations to the cases of anisotropic particle distribution,
more complex material structure and those involving the effect of aggregate size distri-
bution are interesting subjects for the further studies.
 ACKNOWLEDGMENT
 This research is funded by Vietnam National Foundation for Science and Technology
Development (NAFOSTED) under grant number 107.02-2018.306.
 REFERENCES
 [1] E. Herve´ and A. Zaoui. Elastic behaviour of multiply coated fibre-reinforced com-
 posites. International Journal of Engineering Science, 33, (10), (1995), pp. 1419–1433.
 https://doi.org/10.1016/0020-7225(95)00008-l.
 [2] Y. P. Qiu and G. J. Weng. Elastic moduli of thickly coated particle and fiber-
 reinforced composites. Journal of Applied Mechanics, 58, (2), (1991), pp. 388–398.
 https://doi.org/10.1115/1.2897198.
 [3] C.-W. Nan, R. Birringer, D. R. Clarke, and H. Gleiter. Effective thermal conductivity of partic-
 ulate composites with interfacial thermal resistance. Journal of Applied Physics, 81, (10), (1997),
 pp. 6692–6699. https://doi.org/10.1063/1.365209.
 Effective medium approximation for conductivity of coated-inclusion composites with anisotropic coating 241
 [4] H. Le Quang, D. C. Pham, G. Bonnet, and Q.-C. He. Estimations of the ef-
 fective conductivity of anisotropic multiphase composites with imperfect inter-
 faces. International Journal of Heat and Mass Transfer, 58, (1-2), (2013), pp. 175–187.
 https://doi.org/10.1016/j.ijheatmasstransfer.2012.11.028.
 [5] I. V. Andrianov, A. L. Kalamkarov, and G. A. Starushenko. Three-phase model for
 a fiber-reinforced composite material. Composite Structures, 95, (2013), pp. 95–104.
 https://doi.org/10.1016/j.compstruct.2012.07.003.
 [6] M. Hori and S. Nemat-Nasser. Double-inclusion model and overall moduli of
 multi-phase composites. Mechanics of Materials, 14, (3), (1993), pp. 189–206.
 https://doi.org/10.1115/1.2904292.
 [7] D. S. Liu and D. Y. Chiou. Modeling of inclusions with interphases in heterogeneous material
 using the infinite element method. Computational Materials Science, 31, (3-4), (2004), pp. 405–
 420. https://doi.org/10.1016/j.commatsci.2004.05.002.
 [8] Y. M. Shabana. A micromechanical model for composites containing
 multi-layered interphases. Composite Structures, 101, (2013), pp. 265–273.
 https://doi.org/10.1016/j.compstruct.2013.02.008.
 [9] P. D. Chinh and T. A. Binh. Equivalent-inclusion approach for the conductivity of isotropic
 matrix composites with anisotropic inclusions. Vietnam Journal of Mechanics, 38, (4), (2016),
 pp. 239–248. https://doi.org/10.15625/0866-7136/6753.
[10] T. K. Nguyen and D. C. Pham. Equivalent-inclusion approach and effective medium esti-
 mates for elastic moduli of two-dimensional suspensions of compound inclusions. Philosoph-
 ical Magazine, 94, (36), (2014), pp. 4138–4156. https://doi.org/10.1080/14786435.2014.978831.
[11] D. C. Pham and B. V. Tran. Equivalent-inclusion approach and effective medium approxima-
 tions for conductivity of coated-inclusion composites. European Journal of Mechanics-A/Solids,
 47, (2014), pp. 341–348. https://doi.org/10.1016/j.euromechsol.2014.05.010.
[12] B. V. Tran, D. C. Pham, and T. H. G. Nguyen. Equivalent-inclusion approach and effective
 medium approximations for elastic moduli of compound-inclusion composites. Archive of
 Applied Mechanics, 85, (12), (2015), pp. 1983–1995. https://doi.org/10.1007/s00419-015-1031-
 6.
[13] T. N. Quyet, P. D. Chinh, and T. A. Binh. Equivalent-inclusion approach for estimating the
 elastic moduli of matrix composites with non-circular inclusions. Vietnam Journal of Mechan-
 ics, 37, (2), (2015), pp. 123–132. https://doi.org/10.15625/0866-7136/37/2/5659.
[14] B.-V. Tran, D.-C. Pham, and T.-H.-G. Nguyen. Effective medium approxi-
 mation for conductivity of unidirectional coated-fiber composites. Computa-
 tional Thermal Sciences: An International Journal, 9, (1), (2017), pp. 63–76.
 https://doi.org/10.1615/computthermalscien.2017015911.
[15] Z. Hashin and S. Shtrikman. A variational approach to the theory of the effective magnetic
 permeability of multiphase materials. Journal of Applied Physics, 33, (10), (1962), pp. 3125–
 3131. https://doi.org/10.1063/1.1728579.
[16] D. C. Pham. Solutions for the conductivity of multi-coated spheres and spherically symmet-
 ric inclusion problems. Zeitschrift f¨urangewandte Mathematik und Physik, 69, (1), (2018), p. 13.
 https://doi.org/10.1007/s00033-017-0905-6.