Effect of viscosity on slip boundary conditions in rarefied gas flows

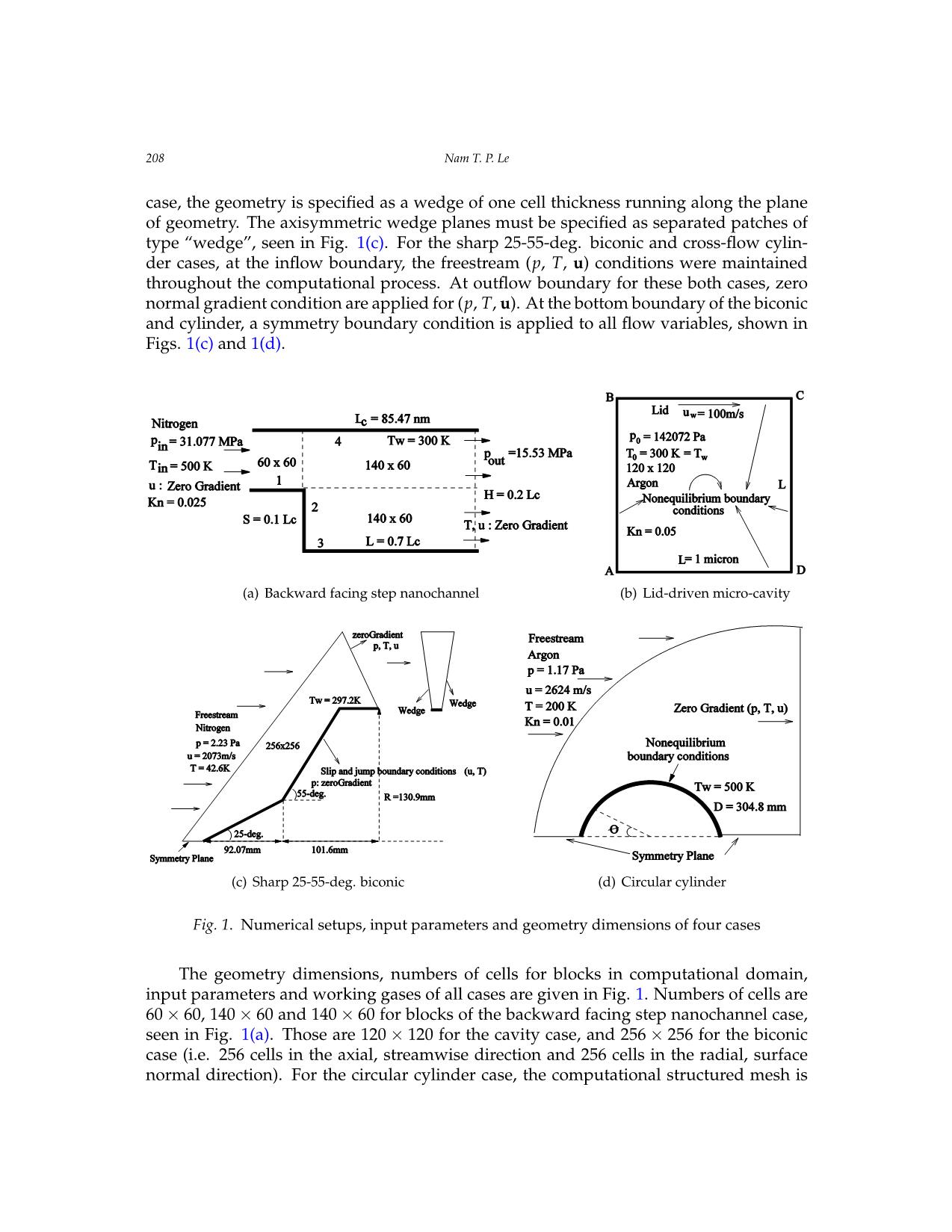
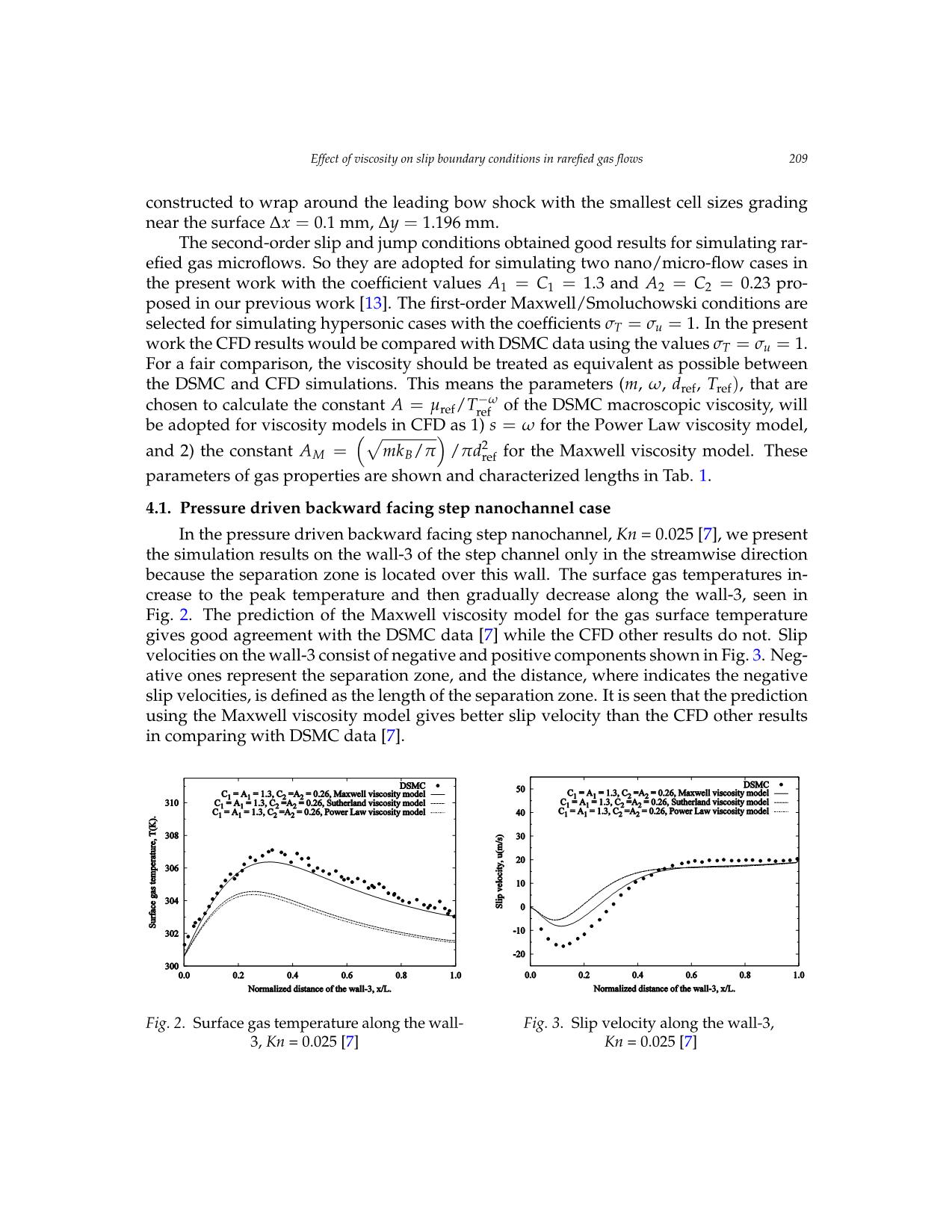
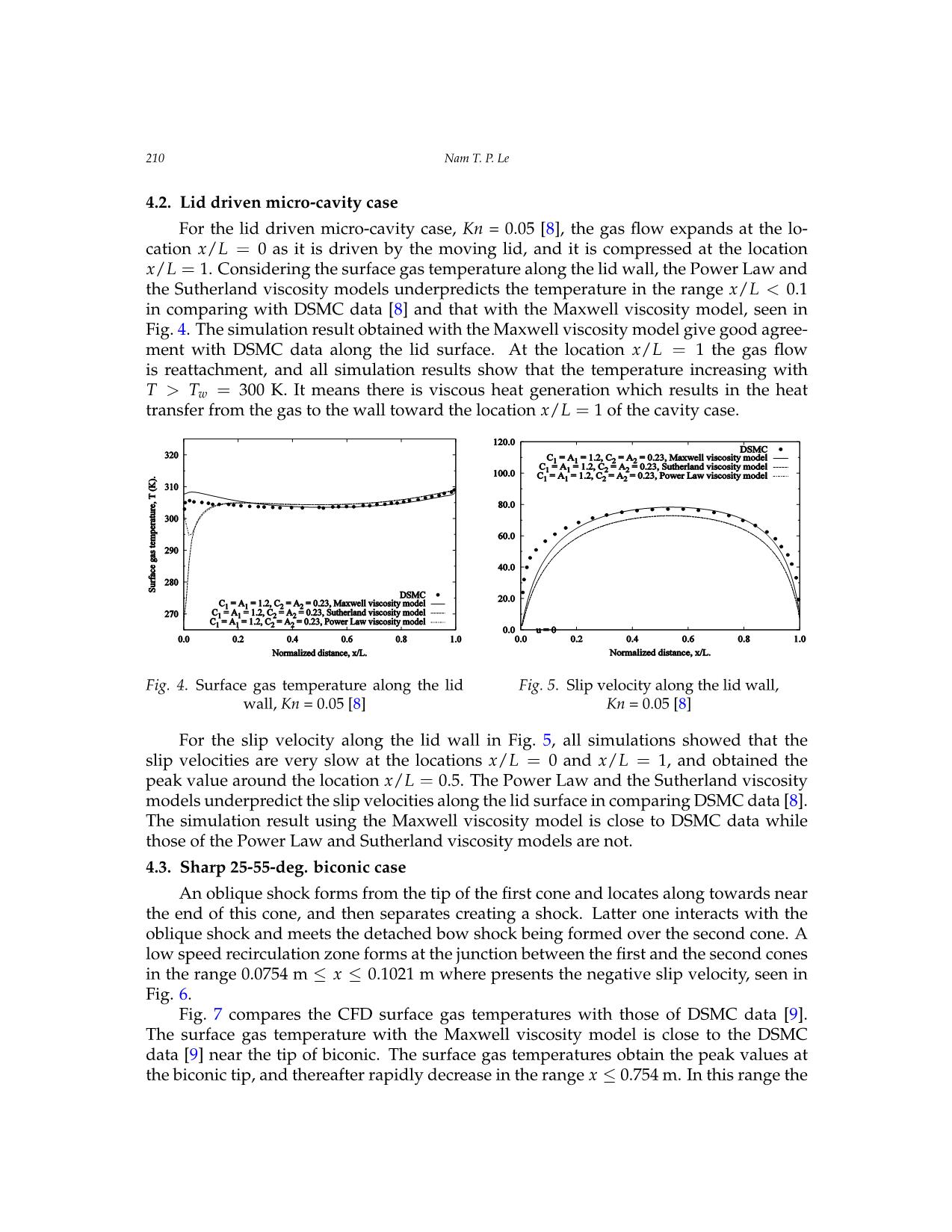
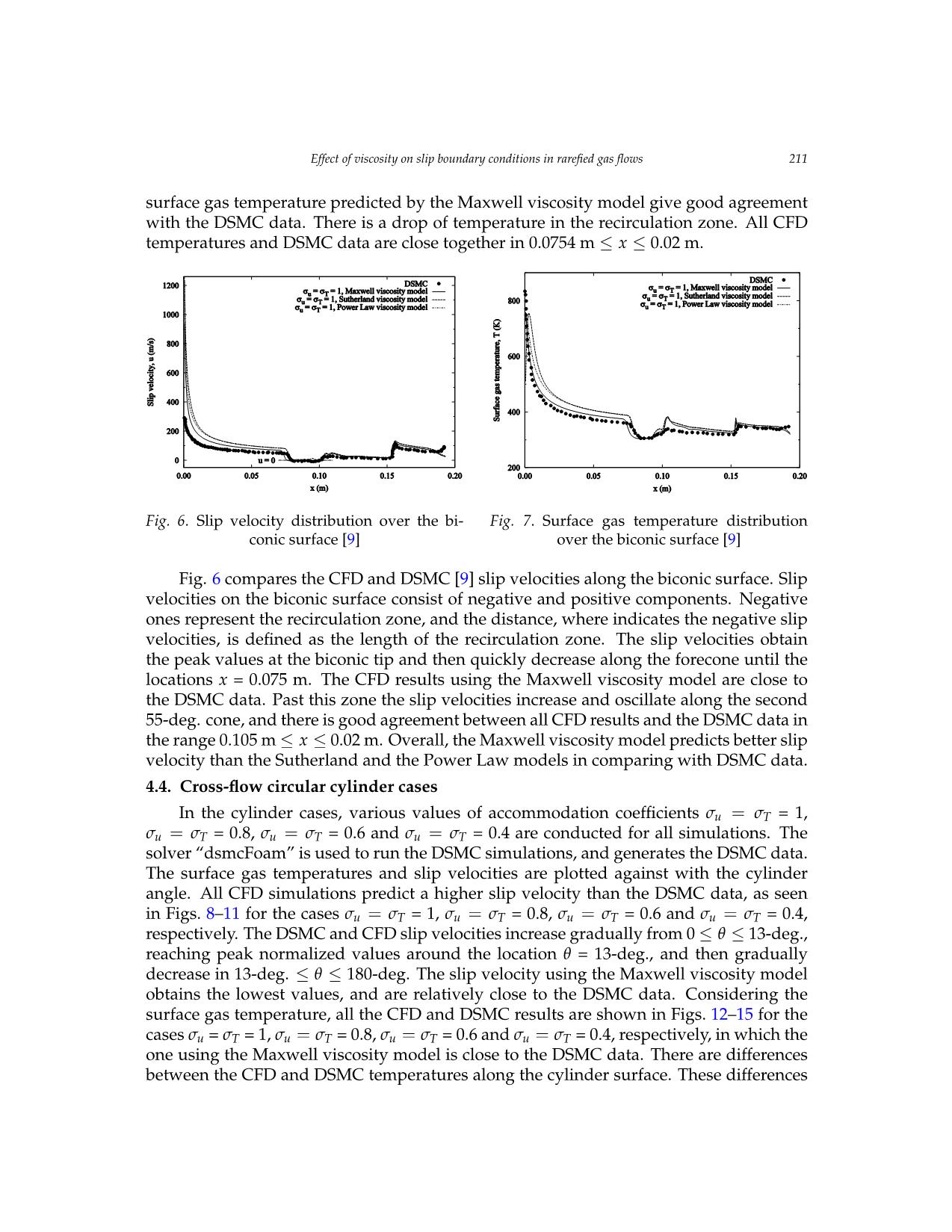
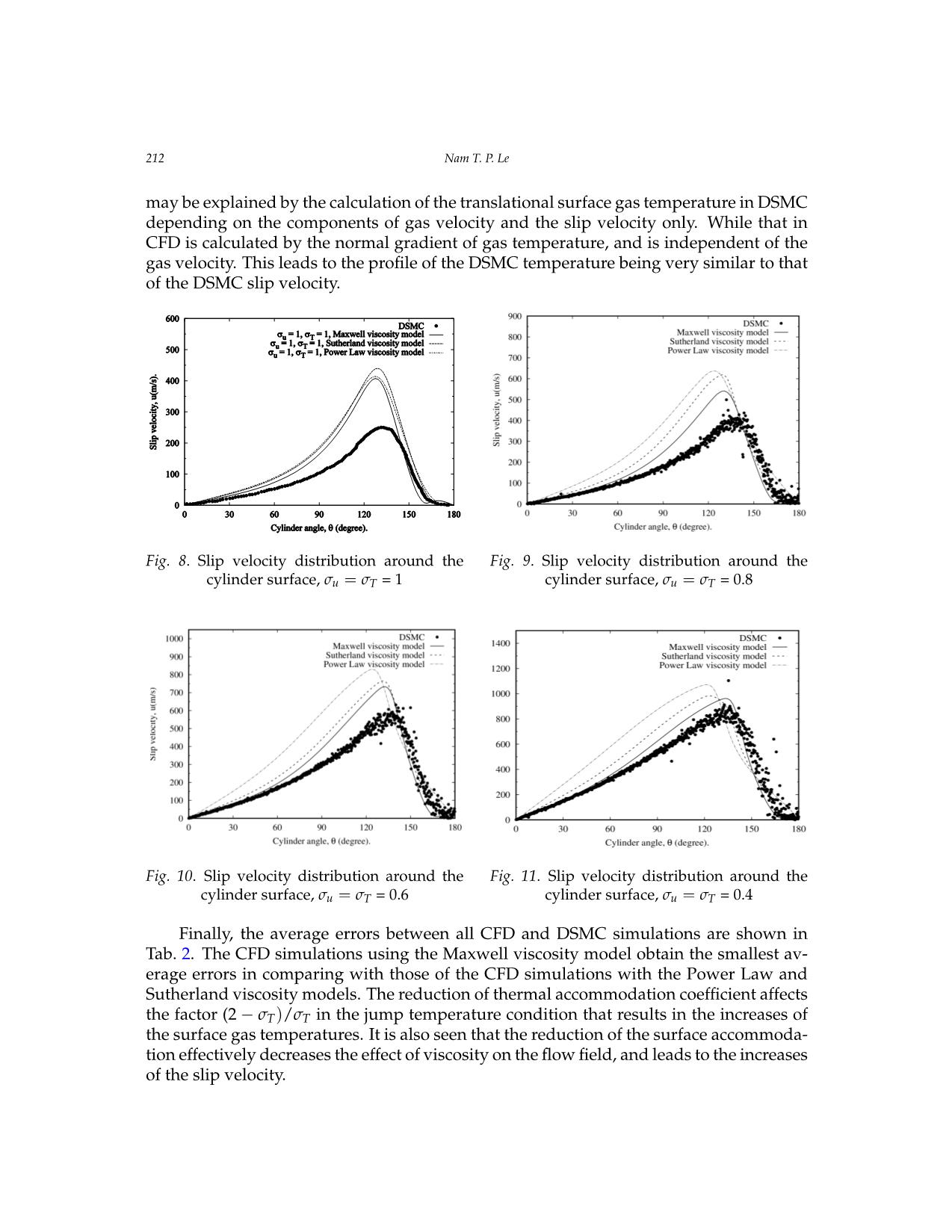
 Vietnam Journal of Mechanics, VAST, Vol.41, No. 3 (2019), pp. 203 – 215
 DOI: https://doi.org/10.15625/0866-7136/13564
 EFFECT OF VISCOSITY ON SLIP BOUNDARY CONDITIONS
 IN RAREFIED GAS FLOWS
 Nam T. P. Le1,2,∗
 1Industrial University of Ho Chi Minh City, Vietnam
 2Ton Duc Thang University, Ho Chi Minh City, Vietnam
 ∗E-mail: letuanphuongnam@tdtu.edu.vn
 Received: 17 January 2019 / Published online: 25 July 2019
 Abstract. The viscosity of gases plays an important role in the kinetic theory of gases
 and in the continuum-fluid modeling of the rarefied gas flows. In this paper we inves-
 tigate the effect of the gas viscosity on the surface properties as surface gas temperature
 and slip velocity in rarefied gas simulations. Three various viscosity models in the liter-
 ature such as the Maxwell, Power Law and Sutherland models are evaluated. They are
 implemented into OpenFOAM to work with the solver “rhoCentralFoam” that solves the
 Navier-Stokes-Fourier equations. Four test cases such as the pressure driven backward
 facing step nanochannel, lid-driven micro-cavity, hypersonic gas flows past the sharp 25-
 55-deg. biconic and the circular cylinder in cross-flow cases are considered for evaluating
 three viscosity models. The simulation results show that, whichever the first-order or
 second-order slip and jump conditions are adopted, the simulation results of the surface
 temperature and slip velocity using the Maxwell viscosity model give good agreement
 with DSMC data for all cases studied.
 Keywords: Sutherland; Power Law; Maxwell viscosity models; rarefied gas flows; slip ve-
 locity; surface gas temperature.
 1. INTRODUCTION
 The accuracy of the Navier–Stokes–Fourier (N–S–F) simulations for rarefied and mi-
croscale gas flows depends on the slip velocity and temperature jump conditions, and
also the constitutive relations supplied, such as the viscosity-temperature relation, ther-
mal conductivity and heat capacity. We did an investigation for the slip and jump con-
ditions in [1] to find the most suitable choice of slip velocity and temperature jump con-
ditions for rarefied gas simulations. Flow regimes in rarefied gas dynamics are charac-
terized by the Knudsen number, Kn, defined as the ratio of gas mean free path (i.e. the
average distance a molecule moves between successive intermolecular collisions) to a
characteristic length of the vehicle body, as free molecular (Kn ≥ 10), transition regime
(0.1 ≤ Kn ≤ 10), slip regime (0.001 ≤ Kn ≤ 0.13), and continuum regime (Kn ≤ 0.001).
 
c 2019 Vietnam Academy of Science and Technology
204 Nam T. P. Le
The CFD method, which solves the Navier–Stokes–Fourier (N–S–F) equations with ap-
propriate slip and jump conditions, may simulate successfully rarefied gas flows in the
slip regime, up to a Knudsen number of 0.1. The Direct Simulation Monte Carlo (DSMC)
method is a commonly used to investigate the rarefied gas flows. But this method is also
very expensive both in computational time and memory requirements.
 The viscosity affects to the accuracy of the N–S–F simulation results through the
shear stress, heat transfer and the Maxwellian mean free path presented in the slip ve-
locity and temperature jump conditions. In gas microflows, the mean free path of the
gas molecules becomes significant relative to the characteristic dimension of the micro-
devices. The action of viscosity can be achieved from a consideration of the transfer of
molecular momentum between two contiguous layers of the mass flow. Momentum is
carried by the molecules from one layer to the other both by direct translation and by in-
termolecular collisions. If this transfer process is undergone then viscous flow occurs [2].
So the viscosity of gases played an important role in the kinetic theory of gases and rar-
efied gas simulations. Various viscosity models such as the constant viscosity, Power
Law and Maxwell viscosity models were investigated for one-dimensional (1D) shock
structure by the CFD and DSMC methods [3,4]. The Maxwell viscosity model gave good
simulation results of the shock structure in comparing with experimental data [5]. The
Sutherland and Power Law viscosity models have been commonly using in CFD simu-
lations. The viscosity of real gases can be matched by a power law over a small temper-
ature range only, because the long-range attractive forces (the van der Waals forces) are
ignored. More realistic is the Sutherland potential which combines a short-range hard
sphere repulsion with a long-range inverse 6th power attractive potential [6]. So far there
is not yet any comparison between these viscosity models in two-dimensional (2D) rar-
efied gas simulations. In this paper three various viscosity models found in the literature
such as Sutherland, Power Law and Maxwell viscosity models are numerically investi-
gated to evaluate their performance in rarefied gas flows in the slip regime (Kn ≤ 0.1).
 Four cases such as the pressure dri ... ous. values of accommodationcalculated by the normal coefficients gradient oσfu gas= temperature,σT = 1, and is independent of the gas velocity. This leads to 
 σ = σ = 0.8, σ = σ = 0.6 and σ = σ = 0.4 are conducted for all simulations. The
Finally, the average errors between all CFD uand DSMCT simulationsu areT shown in Tableu 2. The T the profile of the DSMC temperature being very similar to that of the DSMC slip velocity. 
 solver “dsmcFoam” is used to run the DSMC simulations, and generates the DSMC data.
CFD simulations using the Maxwell viscosity model obtain the smallest average errors in comparing with Finally, the average errors between all CFD and DSMC simulations are shown in Table 2. The 
those of the CFD simulations with the Power LawThe and surface Sutherland gas viscosity temperatures models. The and reduction slip of velocities CFD are simulations plotted using against the Maxwell with theviscosity cylinder model obtain the smallest average errors in comparing with 
thermal accommodation coefficient affects the factorangle. (2 - σT All)/σT CFDin the simulationsjump temperature predict condition a higherthat slipthose velocity of the CFD than simulations the DSMC with data, the Power as seen Law and Sutherland viscosity models. The reduction of 
results in the increases of the surface gas temperatures. It is also seen that the reduction of the surface 
 in Figs.8–11 for the cases σu = σT = 1, σu = σTthermal= 0.8, accommodationσu = σT = 0.6 coefficien and σtu affects= σT the= 0.4,factor (2 - σT)/σT in the jump temperature condition that 
accommodation effectively decreases the effect of viscosity on the flow field, and leads to the increases of results in the increases of the surface gas temperatures. It is also seen that the reduction of the surface 
the slip velocity. respectively. The DSMC and CFD slip velocities increase gradually from 0 ≤ θ ≤ 13-deg.,
 reaching peak normalized values around the locationaccommodationθ = 13-deg.,effectivelyand decreas thenes the gradually effect of viscosity on the flow field, and leads to the increases of 
 the slip velocity. 
 decrease in 13-deg. ≤ θ ≤ 180-deg. The slip velocity using the Maxwell viscosity model
 obtains the lowest values, and are relatively close to the DSMC data. Considering the
 surface gas temperature, all the CFD and DSMC results are shown in Figs. 12–15 for the
 cases σu = σT = 1, σu = σT = 0.8, σu = σT = 0.6 and σu = σT = 0.4, respectively, in which the
 one using the Maxwell viscosity model is close to the DSMC data. There are differences
 between9 the CFD and DSMC temperatures along the cylinder surface. These differences
 9 
 Effect of viscosity on slip boundary conditions in rarefied gas flows 
 212 Nam T. P. Le
 Effect of viscosity mayon slip beboundary explained conditions by in the rarefied calculation gas flows of the translational surface gas temperature in DSMC
 depending on the components of gasNam velocity T. P. Le and the slip velocity only. While that in
 CFD is calculated by the normal gradient of gas temperature, and is independent of the
 gas velocity. This leads to the profile of the DSMC temperature being very similar to that
 Fig. 8. Temperature jump distribution around the Fig. 9. Slip velocity distribution around the cylinder 
 of the DSMC slip velocity. surface, σ = σ = 1. 
 cylinder surface, σu = σT = 1. u T
 Nam T. P. Le 
 Fig. 8.Fig. Slip 10. velocityTemperature distribution jump distribution around around the the Fig. 9Fig.. Slip 11. velocity Slip velocity distribution distribution around around the the 
 Fig.cylinder 9. Slip surface velocity, σ distributionu = σT = 0.8 arou. nd the cylinder cylinder surface, σu = σT = 0.8. 
Fig. 8. Temperature jump distribution around the cylinder surface, σu = σT = 1 cylinder surface, σu = σT = 0.8
 surface, σ = σ = 1. 
cylinder surface, σu = σT = 1. Fig. 12 . Temperatureu T jump distribution around the Fig. 13. Slip velocity distribution around the 
 forebody cylinder surface, σu = σT = 0.6. 
 cylinder surface, σu = σT = 0.6. 
Fig.Fig. 1012.. Temperature jump distributiondistribution around the Fig.Fig.Fig. 1 3 .114. 1Slip. TemperatureSlip velocity velocity distribution jump distribution distribution around arou aroundnd the the the Fig. 15. Slip velocity distribution around the 
 u T cylinder surface, σu = σT = 0.4. 
cylinderforebody surface cylinder, σ surface,u = σT = σ 0.8u = .σ T = 0.6. Fig.cylinder 10cyli. for Slipndebody serurface, s velocityurface cylinder σu, =σ uσ surface,=T distribution =σ 0.T =6. 0.8 σ .= σ = around 0.4. the Fig. 11. Slip velocity distribution around the
 cylinder surface, σu = σT = 0.6 cylinder surface, σu = σT = 0.4
 Table 2: Average errors between the CFD and DSMC simulations of the cylinder cases. 
 Finally, the averageCases errors betweenMaxwell all CFDSutherla and DSMCnd simulationsPower Law are shown in
 viscosity model viscosity model viscosity model 
 Tab.2. The CFD simulations using the Maxwell viscosity model obtain the smallest av-
 erageerrors in comparing withT those ofu the CFDT simulationsu withT the Poweru Law and
 Sutherland viscosity models. The reduction of thermal accommodation coefficient affects
 σu = σT = 1 15.12% 16.84% 28.98% 34.01% 35.65% 33.81% 
 the factor (2 − σT)/σT in the jump temperature condition that results in the increases of
 σu = σT = 0.8 2.84% 13.56% 20.90% 34.82% 55.34% 61.81% 
 the surface gas temperatures. It is also seen that the reduction of the surface accommoda-
 σu = σT = 0.6 1.15% 16.44% 9.56% 29.50% 53.39% 58.78% 
 tion effectively decreases the effect of viscosity on the flow field, and leads to the increases
 of the slip velocity.
 11 
Fig. 14. Temperature jump distribution around the Fig. 15. Slip velocity distribution around the 
 forebody cylinder surface, σu = σT = 0.4. cylinder surface, σu = σT = 0.4. 
 Table 2: Average errors between the CFD and DSMC simulations of the cylinder cases. 
Cases Maxwell Sutherland Power Law 
 viscosity model viscosity model viscosity model 
 T u T u T u 
σu = σT = 1 15.12% 16.84% 28.98% 34.01% 35.65% 33.81% 
σu = σT = 0.8 2.84% 13.56% 20.90% 34.82% 55.34% 61.81% 
σu = σT = 0.6 1.15% 16.44% 9.56% 29.50% 53.39% 58.78% 
 11 
 Effect of viscosity on slip boundary conditions in rarefied gas flows 
 Effect of viscosity on slip boundary conditions in rarefied gas flows Nam T. P. Le 
 Effect of viscosity on slip boundary conditions in rarefied gas flows 213
 Fig. 8. Temperature jump distribution around the Fig. 9. Slip velocity distribution around the cylinder 
 surface, σ = σ = 1. 
 cylinder surface, σu = σT = 1. u T
 Nam T. P. Le 
 Fig. 12. Temperature jump distribution Fig. 13. Temperature jump distribution Fig. 11. Slip velocity distribution around the 
 Fig. Fig.9. Slip 10 .velocity Temperature distribution jump distributionaround the cyli aroundnder the 
 aroundFig. 8 the. Temperature cylinder jumpsurface, distributionσu = σ aroundT = 1 the around the cylinder surface, σu = σT = 0.8
 Fig.cylinder 12. surfaceTemperature, σu = σ jumpT = 0.8 distri. bution around the Fig.cyli nd13er. surfaceSlip , velocity σu = σT = distribution 0.8. around the 
 cylinder surface, σu = σT = 1. surface, σu = σT = 1. 
 for ebody cylinder surface, σu = σT = 0.6. 
 cylinder surface, σu = σT = 0.6. 
 Fig.Fig. 1102.. TemperatureTemperature jump jump distri distributionbution around around the the Fig. Fig.11. 14.Slip Temperature velocity dis jumptribution distribution around around the the Fig. 15. Slip velocity distribution around the 
 Fig. 13. Slip velocity distribution around the 
 Fig.cylinder 14. surface Temperature, σu = σT = jump 0.8. distribution cyliFig.nd 15er .surface Temperature, σu = σT = 0.8 jump. distribution cylinder surface, σu = σT = 0.4. 
 forebody cylinder surface, σu = σT = 0.6. cylinder fsorurface,ebody σ cylinderu = σT = 0.surface,6. σu = σT = 0.4. 
 around the forebody cylinder surface, around the forebody cylinder surface,
 Table 2: Average errors between the CFD and DSMC simulations of the cylinder cases. 
 σu = σT = 0.6 σu = σT = 0.4
 Cases Maxwell Sutherland Power Law 
 Table 2. Average errors between the CFD and DSMC simulations of the cylinderviscosity cases model viscosity model viscosity model 
 T u T u T u 
 Maxwell Sutherland σu = σT = 1 Power15.12% Law 16.84% 28.98% 34.01% 35.65% 33.81% 
 viscosity model viscosity modelσu = σT = 0.8 viscosity2.84% model 13.56% 20.90% 34.82% 55.34% 61.81% 
 Cases 
 T u T uσu = σT = 0.6 T 1.15% 16.44%u 9.56% 29.50% 53.39% 58.78% 
σu = σT = 1 15.12% 16.84% 28.98% 34.01% 35.65% 33.81%
σu = σT = 0.8 2.84% 13.56% 20.90% 34.82% 55.34% 61.81%
 11 
σu =Fig.σT 14.= 0.6Temperature 1.15% jump distribution 16.44% around the 9.56%Fig. 15. 29.50%Slip velocity distribution 53.39% around 58.78% the 
σu = forσebodyT = 0.4 cylinder surface, 8.87% σu = σT = 0.4 6.70%. 16.43%cylinder surface, 17.55% σu = σT = 0. 49.36%4. 36.53%
 Table 2: Average errors between the CFD and DSMC simulations of the cylinder cases. 
 Cases Maxwell Sutherland Power Law 
 viscosity model viscosity model viscosity model 
 T u T u T u 
 σu = σT = 1 15.12% 16.84% 28.98% 34.01% 35.65% 33.81% 
 σu = σT = 0.8 2.84% 13.56% 20.90% 34.82% 55.34% 61.81% 
 σu = σT = 0.6 1.15% 16.44% 9.56% 29.50% 53.39% 58.78% 
 11 
214 Nam T. P. Le
4.5. Discussion
 Although the Sutherland viscosity model has been currently using mostly in the CFD
rarefied gas simulations but the simulation results show that the Maxwell viscosity model
give the good agreement with DSMC data for both the first-order and second-order slip
velocity and temperature jump conditions, and with various accommodation coefficients
in all cases considered. This may be explained that the Maxwell viscosity model was de-
rived based on the net transfer of momentum since the gas molecules across any plane
perpendicular in direction of velocity gradient resulting in the fixed coefficient s = 0.5,
and did not depend on the reference temperature. While the Power Law and the Suther-
land viscosity models were developed based on the intermolecular force law and attrac-
tive force, in which the exponent, s, and constants (AS, TS, AP) are determined from the
limiting theoretical cases or the limited ranges of temperatures in experiments. Com-
paring Eqs. (1) and (4), both of the DSMC and Maxwell viscosity models depend on the
molecular mass and diameter leading to the simulation results of the Maxwell viscosity
model are close to those of DSMC data while two other viscosity models do not.
 5. CONCLUSIONS
 From the simulation results obtained, whichever the slip and jump boundary con-
ditions are adopted, the viscosity models effect the accuracy of the simulation results of
surface gas temperature and slip velocity. The simulation results show that the Maxwell
viscosity model provides better predictions of the surface gas temperature and slip veloc-
ity than the Sutherland and Power Law viscosity models in comparing with the DSMC
data, and pointed out the importance of the viscosity in rarefied gas flow simulations. A
good viscosity model will increase the accuracy of the N–S–F simulations for rarefied gas
flows, and gives better prediction the peak surface gas temperature to design the thermal
protection system in hypersonic vehicles.
 ACKNOWLEDGEMENTS
 This research is funded by Vietnam National Foundation for Science and Technology
Development (NAFOSTED), under grant number 107.03-2018.27.
 REFERENCES
 [1] N. T. P. Le, C. J. Greenshields, and J. M. Reese. Evaluation of nonequilibrium boundary con-
 ditions for hypersonic rarefied gas flows. Progress in Flight Physics, 3, (2012), pp. 217–230.
 https://doi.org/10.1051/eucass/201203217.
 [2] G. N. Patterson. Molecular flow of gases. John Wiley and Sons, (1956).
 [3] C. R. Lilley and M. N. Macrossan. DSMC calculations of shock structure with various viscos-
 ity laws. In The twenty-third Proceeding International Symposium Rarefied Gas Dynamics, (2003),
 pp. 663–670.
 [4] K. B. Jordan. Direct numeric simulation of shock wave structures without the use of artificial viscos-
 ity. PhD thesis, Marquette University, (2011).
 [5] H. Alsmeyer. Density profiles in argon and nitrogen shock waves measured by the ab-
 sorption of an electron beam. Journal of Fluid Mechanics, 74, (3), (1976), pp. 497–513.
 https://doi.org/10.1017/s0022112076001912.
 Effect of viscosity on slip boundary conditions in rarefied gas flows 215
 [6] M. N. Macrossan. µ-DSMC: a general viscosity method for rarefied flow. Journal of Computa-
 tional Physics, 185, (2), (2003), pp. 612–627. https://doi.org/10.1016/s0021-9991(03)00009-3.
 [7] A. M. Mahdavi, N. T. P. Le, E. Roohi, and C. White. Thermal rarefied gas flow investigations
 through micro-/nano-backward-facing step: Comparison of DSMC and CFD subject to hy-
 brid slip and jump boundary conditions. Numerical Heat Transfer, Part A: Applications, 66, (7),
 (2014), pp. 733–755. https://doi.org/10.1080/10407782.2014.892349.
 [8] A. Mohammadzadeh, E. Roohi, H. Niazmand, and S. K. Stefanov. Detailed investigation
 of thermal and hydrodynamic flow behaviour in micro/nano cavity using DSMC and NSF
 equations. In The nineth Proceeding International ASME Conference Nanochannels, Microchannels
 and Minichannels. American Society of Mechanical Engineers, (2011), pp. 341–350.
 [9] J. N. Moss and G. A. Bird. Direct simulation Monte Carlo simulations of hyper-
 sonic flows with shock interactions. AIAA Journal, 43, (12), (2005), pp. 2565–2573.
 https://doi.org/10.2514/1.12532.
[10] A. J. Lofthouse, L. C. Scalabrin, and I. D. Boyd. Velocity slip and temperature jump in hyper-
 sonic aerothermodynamics. Journal of Thermophysics and Heat Transfer, 22, (1), (2008), pp. 38–
 49. https://doi.org/10.2514/1.31280.
[11] J. C. Maxwell. On stresses in rarefied gases arising from inequalities of temperature. Philo-
 sophical Transactions of the Royal Society, 170, (1878), pp. 231–256.
[12] M. Smoluchowski von Smolan. Ueber¨ warmeleitung¨ in verdunnten¨ gasen. Annalender Physik
 und Chemie, 64, (1898), pp. 101–130.
[13] N. T. P. Le and E. Roohi. A new form of the second-order temperature jump
 boundary condition for the low-speed nanoscale and hypersonic rarefied gas
 flow simulations. International Journal of Thermal Sciences, 98, (2015), pp. 51–59.
 https://doi.org/10.1016/j.ijthermalsci.2015.06.017.
[14] OpenFOAM.  Accessed 12/2018.
[15] E. H. Kennard. Kinetic theory of gases. McGraw-Hill, (1938).
[16] S. Chapman and T. G. Cowling. The mathematical theory of non-uniform gases. Cambridge Uni-
 versity Press, (1970).
[17] N. T. P. Le, C. White, J. M. Reese, and R. S. Myong. Langmuir–Maxwell and Langmuir–
 Smoluchowski boundary conditions for thermal gas flow simulations in hypersonic aero-
 dynamics. International Journal of Heat and Mass Transfer, 55, (19-20), (2012), pp. 5032–5043.
 https://doi.org/10.1016/j.ijheatmasstransfer.2012.04.050.