Dynamic responses of an inclined fgsw beam traveled by a moving mass based on a moving mass element theory

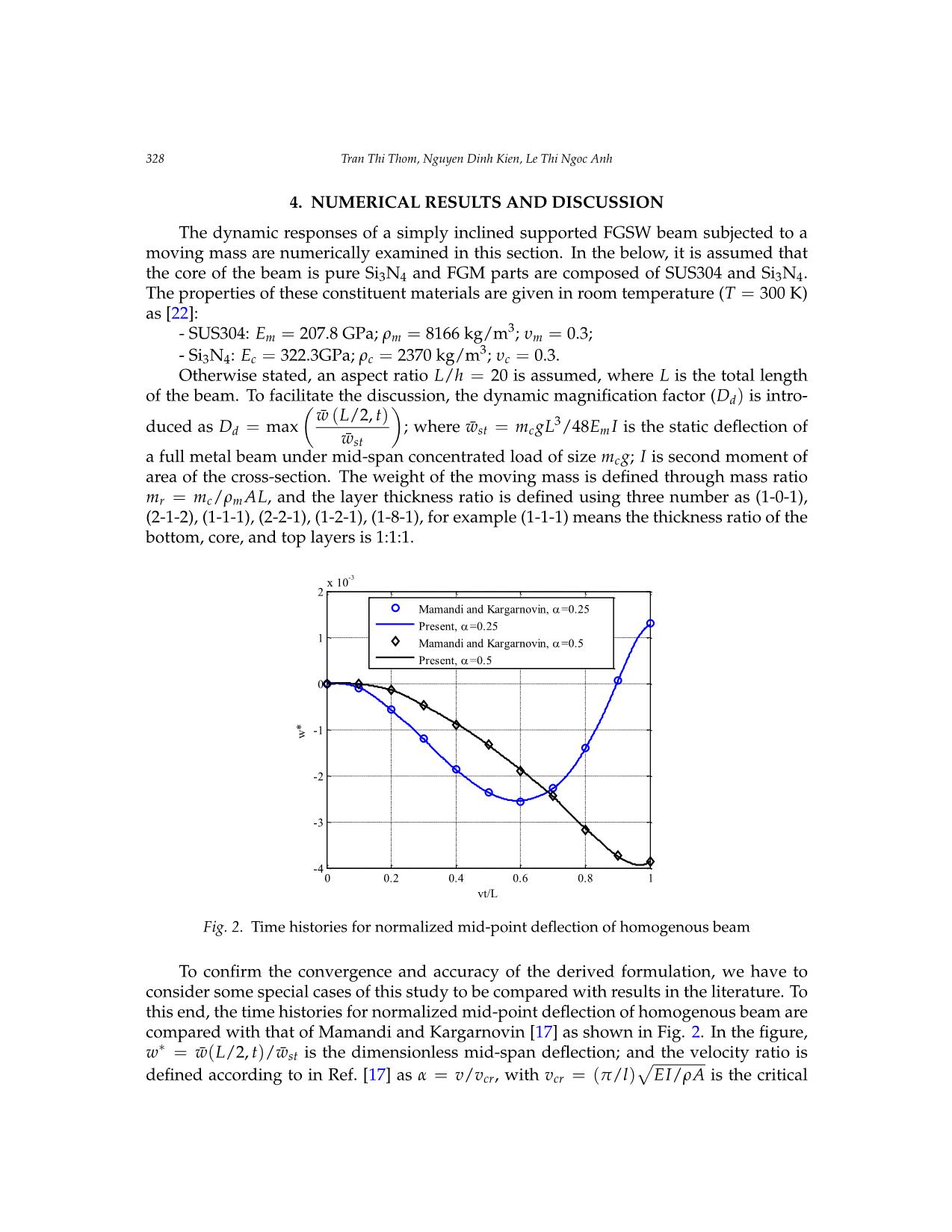
 Vietnam Journal of Mechanics, VAST, Vol.41, No. 4 (2019), pp. 319 – 336
 DOI: https://doi.org/10.15625/0866-7136/14098
 DYNAMIC RESPONSES OF AN INCLINED FGSW BEAM
 TRAVELED BY A MOVING MASS BASED ON A MOVING
 MASS ELEMENT THEORY
 Tran Thi Thom1,2,∗, Nguyen Dinh Kien1,2, Le Thi Ngoc Anh3
 1Institute of Mechanics, VAST, 18 Hoang Quoc Viet, Hanoi, Vietnam
 2Graduate University of Science and Technology, VAST, 18 Hoang Quoc Viet, Hanoi, Vietnam
 3Institute of Applied Information and Mechanics, Ho Chi Minh City, Vietnam
 ∗E-mail: thomtt0101@gmail.com
 Received: 02 August 2019 / Published online: 14 November 2019
 Abstract. Dynamic analysis of an inclined functionally graded sandwich (FGSW) beam
 traveled by a moving mass is studied. The beam is composed of a fully ceramic core and
 two skin layers of functionally graded material (FGM). The material properties of the FGM
 layers are assumed to vary in the thickness direction by a power-law function, and they
 are estimated by Mori–Tanaka scheme. Based on the first-order shear deformation theory,
 a moving mass element, taking into account the effect of inertial, Coriolis and centrifugal
 forces, is derived and used in combination with Newmark method to compute dynamic
 responses of the beam. The element using hierarchical functions to interpolate the dis-
 placements and rotation is efficient, and it is capable to give accurate dynamic responses
 by small number of the elements. The effects of the moving mass parameters, material dis-
 tribution, layer thickness ratio and inclined angle on the dynamic behavior of the FGSW
 beam are examined and highlighted.
 Keywords: inclined FGSW beam; hierarchical functions; moving mass element; Mori–
 Tanaka scheme; dynamic responses.
 1. INTRODUCTION
 Sandwich beams are widely used in the aerospace industry as well as in other indus-
tries due to their high stiffness to weight ratio. Functionally graded materials (FGMs),
initiated by Japanese scientists in 1984, are employed to fabricate functionally graded
sandwich (FGSW) beams to improve their performance in severe conditions. Investiga-
tions on mechanical behavior of the FGSW beams have been recently reported by several
researchers. Bhangale and Ganesan [1] studied thermo-elastic buckling and vibration
behavior of a FGSW beam having constrained viscoelastic core using a finite element for-
mulation. Amirani et al. [2] analyzed free vibration of sandwich beam with FGM core
 
c 2019 Vietnam Academy of Science and Technology
320 Tran Thi Thom, Nguyen Dinh Kien, Le Thi Ngoc Anh
by a mesh-less method. Bui et al. [3] proposed a novel truly mesh-free radial point inter-
polation method to investigate transient responses and natural frequencies of sandwich
beams with FGM core. Using a mesh-free boundary-domain integral equation method,
Yang et al. [4] studied free vibration of the FGSW beams. Based on a refined shear defor-
mation theory and a quasi-3D theory, Vo et al. [5,6] derived finite element formulations
for free vibration and buckling analyses of FGSW beams. Nguyen et al. [7] obtained an
analytical solution for buckling and vibration analysis of FGSW beams using a quasi-3D
shear deformation theory. Again, a quasi-3D theory is used by Vo et al. [8] to study static
behavior of FGSW beams. Finite element model and Navier solutions are developed by
the authors to determine the displacements and stresses of FGSW beams with various
boundary conditions. Su et al. [9] considered free vibration of FGSW beams resting on
a Pasternak elastic foundation. The effective material properties of FGM are estimated
by both Voigt model and Mori–Tanaka scheme, and the governing equations are solved
using the modified Fourier series method. Based on Timoshenko beam theory, S¸ims¸ek
and Al-shujairi [10] examined static, free and forced vibration of FGSW beams under
the action of two moving harmonic loads. The equations of the motion are obtained by
the authors using Lagrange’s equations, and they are solved by the implicit Newmark-β
method.
 The problem of beams traveled by a moving mass has drawn much attention from
scientists [11–15]. The inertial effects of the moving mass including Coriolis, inertia and
centrifugal forces are taken into consideration by the authors. Most of the works, how-
ever considered the horizontal beams. When the beams are inclined, then the approaches
presented in the foregoing researches cannot be directly applied to solve the problem. For
this reason, Wu [16] used the theory of moving mass element to determine the dynamic
response of an inclined homogeneous Euler-Bernoulli beam due to a moving mass. The
property matrices of the moving mass element are derived by taking into account of the
effects of inertial force, Coriolis force and centrifugal force induced by a moving mass.
Mamandi and Kargarnovin [17] studied dynamic behavior of inclined pinned-pinned
Timoshenko beams made of linear, homogenous and isot ...  In Fig. 5, the relation between the dynamic magnification factor Dd and the moving mass velocity is 
 illustrated with different mass ratio and inclined angle of the beam. As seen from the figure, the relation 
 between Dd and v is similar to that of isotropic beams under a moving load, that is, the factor Dd both 
 increases and decreases when the velocity of moving mass is low. When moving mass velocity increases, 
 the factor Dd increases and it reaches a maximum value. This dependency rule is true for any values of the 
 mass ratio and inclined angle of the beam. In addition, the increase in the mass ratio leads to the decrease 
 in the factor Dd and the factor Dd reaches the maximum value at the lower velocity of moving mass. Also, 
 it is seen from this figure that the factor Dd decreases as the inclined angle of the beam increases. 
 13 
 Dynamic responses of an inclined FGSW beam traveled by a moving mass based on a moving mass element theory 333
of moving mass is low. When moving mass velocity increases, the factor Dd increases
and it reaches a maximum value. This dependency rule is true for any values of the mass
ratio and inclined angle of the beam. In addition, the increase in the mass ratio leads to
the decrease in the factor Dd and the factor Dd reaches the maximum value at the lower
velocity of moving mass. Also, it is seen from this figure that the factor Dd decreases as
the inclined angle of the beam increases.
 m =0.25 m =0.5 m =0.75 m =1
 r r r r
 2.5 2.5
 (a) =0 (b) = /12
 2 2
 d 1.5 d 1.5
 D D
 1 1
 0.5 0.5
 50 100 150 200 250 300 0 50 100 150 200 250 300
 v (m/s) v (m/s)
 2.5 2.5
 (c) = /6 (d) = /4
 2 2
 d
 d 1.5
 1.5 D
 D
 1 1
 0.5 0.5
 0 50 100 150 200 250 300 0 50 100 150 200 250 300
 damping and stiffness matricesv (m/s) of the moving mass element generated by the vinteraction (m/s) forces including 
 the inertia force, Coriolis force and centrifugal force. These matrices must be added to the corresponding 
 onesFig. 5.of Variationthe entire of inclined the dynamic beam magnification itself to receive factor ofthe (1 instantaneous-2-1) beam with overall different mass, mass damping ratio and andinclined stiffness angle: 
 Fig. 5. Variationmatrices.n=1 of The the system dynamic of motion magnification equations is solved with factor the aid of of (1-2-1) Newmark beam method. withThe accuracy different of the mass ratio
 derived formulation was validated by comparing the numericaln results= obtained in the present paper with 
 the availableIn Fig. data 6 and in theFig. literature. 7, the thicknessand The numerical inclined distribution results angle: of showthe normalized a clear effect1 axial of stressthe gradient at mid index,-span sectionthe layer of 
 thickness(1-1-1) beam ratio, and moving (4-2- 1)mass beam speed, are depicted mass ratio for and various the inclined values ofangle inclined of th eangle beam of on the the beam dynamic with responsev=30 m/s 
 ofand the v =100beam. m/s, respectively. The stress in these figures was computed at the time when the moving mass 
 arrives at the mid-span of the inclined beam, and it was normalized as  /  , where  = PLh/8I, 
 0.5 0.5 xx 0 0 
 P=100 kN. At a given value of moving mass velocity, the maximum amplitude of both the compressive 
 =0 =0
 and tensile stresses decrease as the inclined angle of the beam increases. Thus, by raising the inclined angle 
 of the beam, we could= /12 decrease not only the dynamic magnification factor,= /12but also the maximum amplitude 
 of 0.25the axial stress.= Specially, /6 it can be observed from these0.25 figures that =in /6the case beam is unsymmetrical 
 (Fig. 6b, 7b), the stress= /4 does not vanish at the mid-span. = /4
 5. CONCLUSION 
 0 0
 z/h
 z/h
 The dynamic analysis of an inclined FGSW beam subjected to moving mass is studied using the first-
 order shear deformation theory. The effective material properties of FGSW beam are estimated by Mori– 
 T-0.25anaka’s scheme. The hierarchical functions are used to-0.25 interpolate the displacements at the contact point 
 i between the moving mass and beam element, and these shape functions are also used to interpolate the 
 kinematic variables of the beam. The theory of moving mass element has been used to establish the mass, 
 (a) (1-1-1) (b) (4-2-1)
 -0.5 -0.5 
 -10 -5 0 5 10 14 -10 -5 0 5 10
 * * 
 Fig. 6. Thickness distribution of normalized axial stress at mid-span section of inclined FGSW beam with different 
Fig. 6. Thickness distribution of normalizedinclined angle: axial v=30 m/s, stress n=1, mr=0.5 at mid-span section of inclined FGSW
 beam with different inclined angle: v = 30 m/s, n = 1, mr = 0.5
 0.5 0.5 
 =0 =0
 = /12 = /12
 0.25 = /6 0.25 = /6
 = /4 = /4
 0 0
 z/h
 z/h
 -0.25 -0.25
 (a) (1-1-1) (b) (4-2-1)
 -0.5 -0.5 
 -10 -5 0 5 10 15 -10 -5 0 5 10 15
 *
 * 
 Fig. 7. Thickness distribution of normalized axial stress at mid-span section of inclined FGSW beam with different 
 inclined angle: v=100 m/s, n=1, mr=0.5 
 15 
 damping and stiffness matrices of the moving mass element generated by the interaction forces including 
 the inertia force, Coriolis force and centrifugal force. These matrices must be added to the corresponding 
 ones of the entire inclined beam itself to receive the instantaneous overall mass, damping and stiffness 
 matrices. The system of motion equations is solved with the aid of Newmark method. The accuracy of the 
 derived formulation was validated by comparing the numerical results obtained in the present paper with 
 the available data in the literature. The numerical results show a clear effect of the gradient index, the layer 
 thickness ratio, moving mass speed, mass ratio and the inclined angle of the beam on the dynamic response 
 of the beam. 
 0.5 0.5 
 =0 =0
 = /12 = /12
 0.25 = /6 0.25 = /6
 = /4 = /4
 0 0
 z/h
 z/h
 -0.25 -0.25
 (a) (1-1-1) (b) (4-2-1)
 -0.5 -0.5 
 -10 -5 0 5 10 -10 -5 0 5 10
 * * 
334Fig. 6. Thickness distribution Tran Thiof normalized Thom, Nguyen axial stress Dinh at mid Kien,-span Lesection Thi of Ngoc inclined Anh FGSW beam with different 
 inclined angle: v=30 m/s, n=1, mr=0.5 
 0.5 0.5 
 =0 =0
 = /12 = /12
 0.25 = /6 0.25 = /6
 = /4 = /4
 0 0
 z/h
 z/h
 -0.25 -0.25
 (a) (1-1-1) (b) (4-2-1)
 -0.5 -0.5 
 -10 -5 0 5 10 15 -10 -5 0 5 10 15
 *
 * 
 Fig. 7. Thickness distribution of normalized axial stress at mid-span section of inclined FGSW beam with different 
Fig. 7. Thickness distribution of normalizedinclined angle: axialv=100 m/s, stress n=1, m atr=0.5 mid-span section of inclined FGSW
 beam with different inclined angle:15 v = 100 m/s, n = 1, mr = 0.5
 In Fig.6 and Fig.7, the thickness distributions of the normalized axial stress at
mid-span section of (1-1-1) beam and (4-2-1) beam are depicted for various values of
inclined angle of the beam with v = 30 m/s and v = 100 m/s, respectively. The stress in
these figures was computed at the time when the moving mass arrives at the mid-span
 ∗
of the inclined beam, and it was normalized as σ = σxx/σ0, where σ0 = PLh/8I, P =
100 kN. At a given value of moving mass velocity, the maximum amplitude of both the
compressive and tensile stresses decrease as the inclined angle of the beam increases.
Thus, by raising the inclined angle of the beam, we could decrease not only the dynamic
magnification factor, but also the maximum amplitude of the axial stress. Specially, it can
be observed from these figures that in the case beam is unsymmetrical (Fig.6(b),7(b)),
the stress does not vanish at the mid-span.
 5. CONCLUSION
 The dynamic analysis of an inclined FGSW beam subjected to moving mass is stud-
ied using the first-order shear deformation theory. The effective material properties of
FGSW beam are estimated by Mori–Tanaka’s scheme. The hierarchical functions are
used to interpolate the displacements at the contact point i between the moving mass
and beam element, and these shape functions are also used to interpolate the kinematic
variables of the beam. The theory of moving mass element has been used to establish
the mass, damping and stiffness matrices of the moving mass element generated by the
interaction forces including the inertia force, Coriolis force and centrifugal force. These
matrices must be added to the corresponding ones of the entire inclined beam itself to re-
ceive the instantaneous overall mass, damping and stiffness matrices. The system of mo-
tion equations is solved with the aid of Newmark method. The accuracy of the derived
formulation was validated by comparing the numerical results obtained in the present
paper with the available data in the literature. The numerical results show a clear effect
of the gradient index, the layer thickness ratio, moving mass speed, mass ratio and the
inclined angle of the beam on the dynamic response of the beam.
 Dynamic responses of an inclined FGSW beam traveled by a moving mass based on a moving mass element theory 335
 ACKNOWLEDGMENTS
 This research is funded by Vietnam National Foundation for Science and Technology
Development (NAFOSTED) under Grant Number 107.02-2018.23. The authors gratefully
thank the Reviewers for their valuable comments and suggestions to improve the quality
of the paper.
 REFERENCES
 [1] R. K. Bhangale and N. Ganesan. Thermoelastic buckling and vibration behavior of a func-
 tionally graded sandwich beam with constrained viscoelastic core. Journal of Sound and Vi-
 bration, 295, (1-2), (2006), pp. 294–316. https://doi.org/10.1016/j.jsv.2006.01.026.
 [2] M. C. Amirani, S. M. R. Khalili, and N. Nemati. Free vibration analysis of sandwich beam
 with FG core using the element free Galerkin method. Composite Structures, 90, (3), (2009),
 pp. 373–379. https://doi.org/10.1016/j.compstruct.2009.03.023.
 [3] T. Q. Bui, A. Khosravifard, C. Zhang, M. R. Hematiyan, and M. V. Golub. Dy-
 namic analysis of sandwich beams with functionally graded core using a truly mesh-
 free radial point interpolation method. Engineering Structures, 47, (2013), pp. 90–104.
 https://doi.org/10.1016/j.engstruct.2012.03.041.
 [4] Y. Yang, C. C. Lam, K. P. Kou, and V. P. Iu. Free vibration analysis of the functionally
 graded sandwich beams by a meshfree boundary-domain integral equation method. Com-
 posite Structures, 117, (2014), pp. 32–39. https://doi.org/10.1016/j.compstruct.2014.06.016.
 [5] T. P. Vo, H.-T. Thai, T.-K. Nguyen, A. Maheri, and J. Lee. Finite element model
 for vibration and buckling of functionally graded sandwich beams based on a
 refined shear deformation theory. Engineering Structures, 64, (2014), pp. 12–22.
 https://doi.org/10.1016/j.engstruct.2014.01.029.
 [6] T. P. Vo, H.-T. Thai, T.-K. Nguyen, F. Inam, and J. Lee. A quasi-3D theory for vibration and
 buckling of functionally graded sandwich beams. Composite Structures, 119, (2015), pp. 1–12.
 https://doi.org/10.1016/j.compstruct.2014.08.006.
 [7] T.-K. Nguyen, T. P. Vo, B.-D. Nguyen, and J. Lee. An analytical solution for
 buckling and vibration analysis of functionally graded sandwich beams using a
 quasi-3D shear deformation theory. Composite Structures, 156, (2016), pp. 238–252.
 https://doi.org/10.1016/j.compstruct.2015.11.074.
 [8] T. P. Vo, H.-T. Thai, T.-K. Nguyen, F. Inam, and J. Lee. Static behaviour of functionally graded
 sandwich beams using a quasi-3D theory. Composites Part B: Engineering, 68, (2015), pp. 59–
 74. https://doi.org/10.1016/j.compositesb.2014.08.030.
 [9] Z. Su, G. Jin, Y. Wang, and X. Ye. A general Fourier formulation for vibration analysis of func-
 tionally graded sandwich beams with arbitrary boundary condition and resting on elastic
 foundations. Acta Mechanica, 227, (5), (2016), pp. 1493–1514. https://doi.org/10.1007/s00707-
 016-1575-8.
[10] M. S¸ims¸ek and M. Al-shujairi. Static, free and forced vibration of functionally graded (FG)
 sandwich beams excited by two successive moving harmonic loads. Composites Part B: Engi-
 neering, 108, (2017), pp. 18–34. https://doi.org/10.1016/j.compositesb.2016.09.098.
[11] T. O. Awodola, S. A. Jimoh, and B. B. Awe. Vibration under variable magnitude moving
 distributed masses of non-uniform Bernoulli-Euler beam resting on Pasternak elastic foun-
 dation. Vietnam Journal of Mechanics, 41, (1), (2019), pp. 63–78. https://doi.org/10.15625/0866-
 7136/12781.
336 Tran Thi Thom, Nguyen Dinh Kien, Le Thi Ngoc Anh
[12] A. O. Cifuentes. Dynamic response of a beam excited by a moving mass. Finite Elements in
 Analysis and Design, 5, (3), (1989), pp. 237–246. https://doi.org/10.1016/0168-874x(89)90046-
 2.
[13] E. Esmailzadeh and M. Ghorashi. Vibration analysis of a Timoshenko beam subjected
 to a travelling mass. Journal of Sound and Vibration, 199, (4), (1997), pp. 615–628.
 https://doi.org/10.1016/s0022-460x(96)99992-7.
[14] M. S¸ims¸ek. Vibration analysis of a functionally graded beam under a moving mass
 by using different beam theories. Composite Structures, 92, (4), (2010), pp. 904–917.
 https://doi.org/10.1016/j.compstruct.2009.09.030.
[15] I. Esen, M. A. Koc, and Y. Cay. Finite element formulation and analysis of a func-
 tionally graded Timoshenko beam subjected to an accelerating mass including iner-
 tial effects of the mass. Latin American Journal of Solids and Structures, 15, (10), (2018).
 https://doi.org/10.1590/1679-78255102.
[16] J.-J. Wu. Dynamic analysis of an inclined beam due to moving loads. Journal of Sound and
 Vibration, 288, (1-2), (2005), pp. 107–131. https://doi.org/10.1016/j.jsv.2004.12.020.
[17] A. Mamandi and M. H. Kargarnovin. Dynamic analysis of an inclined Timoshenko beam
 traveled by successive moving masses/forces with inclusion of geometric nonlinearities.
 Acta Mechanica, 218, (1-2), (2010), pp. 9–29. https://doi.org/10.1007/s00707-010-0400-z.
[18] E. Bahmyari, S. R. Mohebpour, and P. Malekzadeh. Vibration analysis of inclined laminated
 composite beams under moving distributed masses. Shock and Vibration, 2014, (2014), pp. 1–
 12. https://doi.org/10.1155/2014/750916.
[19] J. E. Akin. Finite elements for analysis and design. Academic Press, London, (1994).
[20] A. Tessler and S. B. Dong. On a hierarchy of conforming Timoshenko beam ele-
 ments. Computers & Structures, 14, (3-4), (1981), pp. 335–344. https://doi.org/10.1016/0045-
 7949(81)90017-1.
[21] D. K. Nguyen and T. T. Tran. Free vibration of tapered BFGM beams using an efficient shear
 deformable finite element model. Steel and Composite Structures, 29, (3), (2018), pp. 363–377.
 https://doi.org/10.12989/scs.2018.29.3.363.
[22] A. Fallah and M. M. Aghdam. Nonlinear free vibration and post-buckling analysis of func-
 tionally graded beams on nonlinear elastic foundation. European Journal of Mechanics - A/-
 Solids, 30, (4), (2011), pp. 571–583. https://doi.org/10.1016/j.euromechsol.2011.01.005.