Định lượng độ rối và viễn tải lượng tử với trạng thái thêm và bớt một photon lên hai mode kết hợp

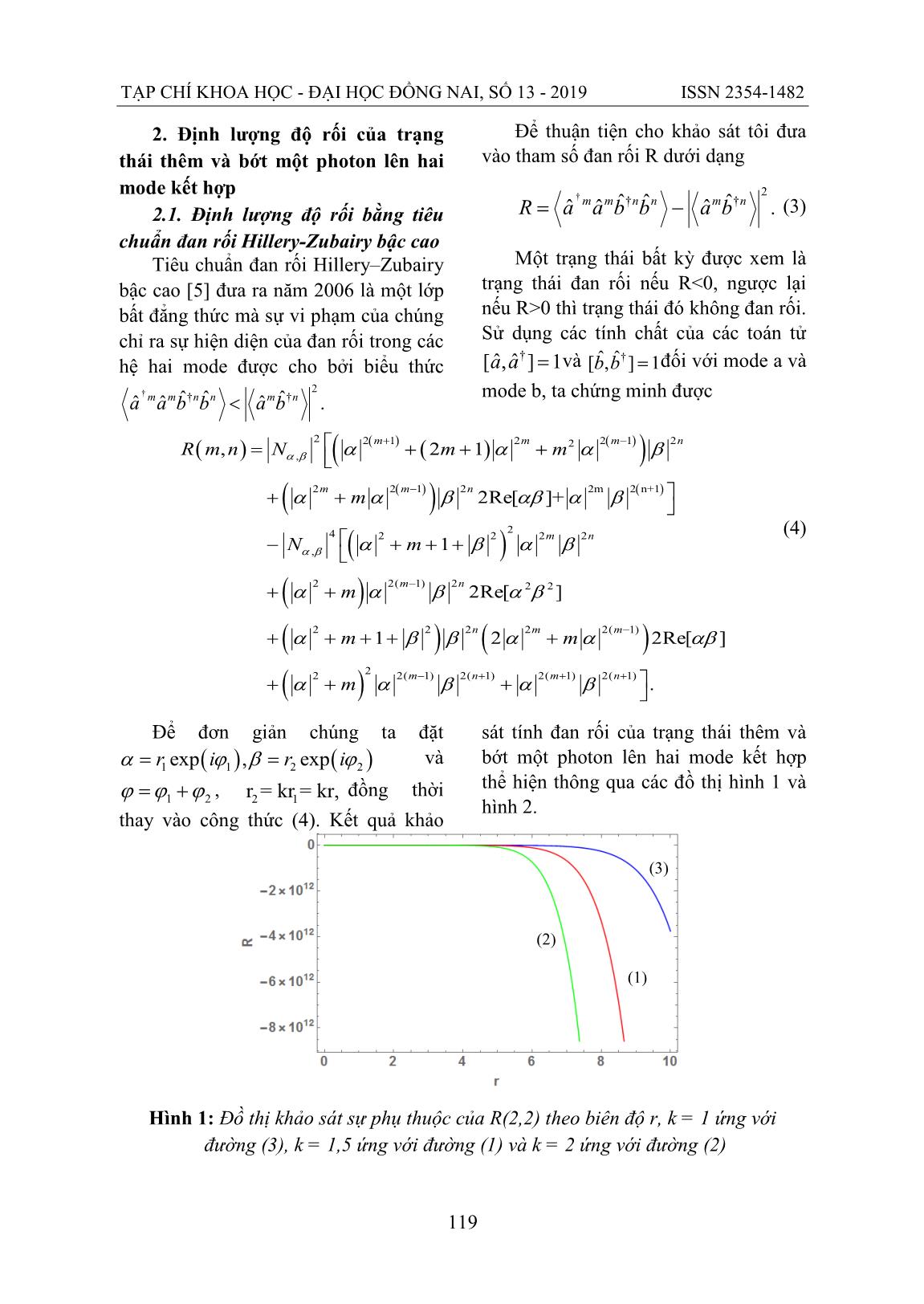
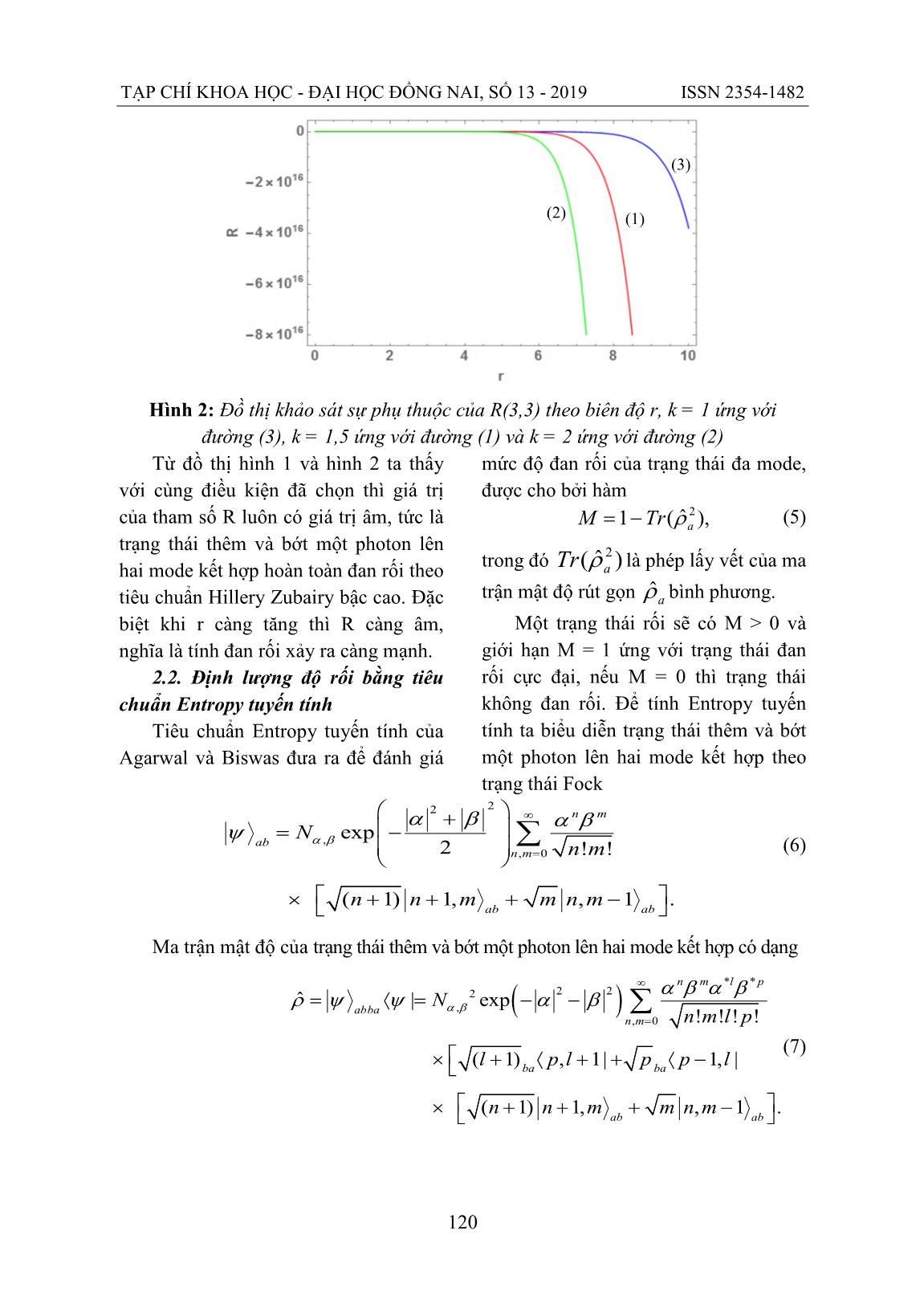
TẠP CHÍ KHOA HỌC - ĐẠI HỌC ĐỒNG NAI, SỐ 13 - 2019 ISSN 2354-1482 
118 
ĐỊNH LƯỢNG ĐỘ RỐI VÀ VIỄN TẢI LƯỢNG TỬ VỚI TRẠNG THÁI 
THÊM VÀ BỚT MỘT PHOTON LÊN HAI MODE KẾT HỢP 
Phạm Thị Hằng1 
Trần Quang Đạt2 
Trương Minh Đức1 
TÓM TẮT 
Trong bài báo này, chúng tôi định lượng độ rối và viễn tải lượng tử của trạng 
thái thêm và bớt một photon lên hai mode kết hợp. Bằng việc sử dụng đồng thời 
tiêu chuẩn đan rối Hillery–Zubairy bậc cao và tiêu chuẩn Entropy tuyến tính, 
chúng tôi thu được kết quả trạng thái này là một trạng thái hoàn toàn đan rối khi 
ta chọn các tham số trạng thái phù hợp. Tiếp theo chúng tôi tiến hành viễn tải 
lượng tử với trạng thái thêm và bớt một photon lên hai mode kết hợp, sau đó đánh 
giá mức độ thành công của quá trình viễn tải thông qua độ trung thực trung bình. 
Kết quả cho thấy rằng quá trình viễn tải lượng tử là thành công khi ta chọn các 
tham số trạng thái phù hợp. 
Từ khóa: Tiêu chuẩn đan rối Hillery-Zubairy bậc cao, tiêu chuẩn Entropy tuyến 
tính,viễn tải lượng tử, độ trung thực trung bình 
1. Giới thiệu 
Vào năm 1963 Glauber [1] và 
Sudar Shan [2] đã đưa ra trạng thái kết 
hợp, đó là trạng thái tương ứng với giá 
trị thăng giáng nhỏ nhất suy ra từ hệ 
thức bất định Heisenberg. Sau đó 
Agarwal và Tara đã đề xuất ý tưởng về 
trạng thái kết hợp thêm photon [3] và 
cũng đã chứng minh được nó là một 
trạng thái phi cổ điển năm 1991. Việc 
tạo ra các trạng thái phi cổ điển có ý 
nghĩa rất quan trọng cho sự phát triển 
khoa học và công nghệ thông tin lượng 
tử. Một phương pháp quan trọng để tạo 
ra một trạng thái phi cổ điển mới là việc 
thêm và bớt photon vào một trạng thái 
vật lý. Trạng thái thêm và bớt một 
photon lên hai mode kết hợp có dạng 
( )†, ˆˆ ,ab a bN a bα βψ α β= + (1) 
trong đó 
, 2 2
1
1 2Re[ ]
Nα β
α β αβ
=
+ + + 
(2) 
là hệ số chuẩn hóa, †aˆ và bˆ lần lượt là 
toán tử sinh đối với mode a và toán tử 
hủy đối với mode b của trường điện từ 
với hai mode a và b độc lập. Việc khảo 
sát các tính chất phi cổ điển của trạng 
thái thêm và bớt một photon lên hai 
mode kết hợp đã được tác giả Nguyễn 
Hữu Luân [4] nghiên cứu. Tuy nhiên, 
việc định lượng độ rối và viễn tải lượng 
tử với trạng thái thêm và bớt một 
photon lên hai mode kết hợp vẫn chưa 
được đề cập đến. Vì vậy, trong bài báo 
này chúng tôi định lượng độ rối và viễn 
tải lượng tử với trạng thái thêm và bớt 
một photon lên hai mode kết hợp. 
1Trường Đại học Sư phạm – Đại học Huế 
Email: tmduc2009@gmail.com 
2 Trường Đại học Giao thông vận tải – Phân hiệu 
tại TP. Hồ Chí Minh 
TẠP CHÍ KHOA HỌC - ĐẠI HỌC ĐỒNG NAI, SỐ 13 - 2019 ISSN 2354-1482 
119 
2. Định lượng độ rối của trạng 
thái thêm và bớt một photon lên hai 
mode kết hợp 
2.1. Định lượng độ rối bằng tiêu 
chuẩn đan rối Hillery-Zubairy bậc cao 
Tiêu chuẩn đan rối Hillery–Zubairy 
bậc cao [5] đưa ra năm 2006 là một lớp 
bất đẳng thức mà sự vi phạm của chúng 
chỉ ra sự hiện diện của đan rối trong các 
hệ hai mode được cho bởi biểu thức 
† 2† †ˆ ˆ ˆˆ ˆ ˆ .m m n n m na a b b a b< 
Để thuận tiện cho khảo sát tôi đưa 
vào tham số đan rối R dưới dạng 
† 2† †ˆ ˆ ˆˆ ˆ ˆ .m m n n m nR a a b b a b= − (3) 
Một trạng thái bất kỳ được xem là 
trạng thái đan rối nếu R<0, ngược lại 
nếu R>0 thì trạng thái đó không đan rối. 
Sử dụng các tính chất của các toán tử 
†ˆ ˆ[ , ] 1a a = và †ˆ ˆ[ , ] 1b b = đối với mode a và 
mode b, ta chứng minh được 
( ) ( ) ( ) ( )( )
( )( ) ( )
( )
( )
( ) ( )
( )
2 2 1 2 2 1 22
,
2 2 1 2 2m 2 n+1
4 2 2 2 2
,
2 2( 1) 2 2 2
2 2 2 2 2( 1)
22 2( 1) 2
2
( 1) 2( 1) 2( 1)
, 2 1
2Re[ ]+
1
2Re[ ]
1 2 2Re[ ]
.
m m m n
m m n
m n
m n
n m m
m n m n
R m n N m m
m
N m
m
m m
m
α β
α β
α α α β
α α β αβ α β
α β α β
α α β α β
α β β α α αβ
α α β α β
+ −
−
−
−
− + + +
= + + +
+ 
− + + +
+
+ + + + +
+ + +


+

+


 (4) 
Để đơn giản chúng ta đặt 
( ) ( )1 1 2 2exp , expr i r iα ϕ β ϕ= = và 
1 2ϕ ϕ ϕ= + , 2 1r = kr = kr, đồng thời 
thay vào công thức (4). Kết quả khảo 
sát tính đan rối của trạng thái thêm và 
bớt một photon lên hai mode kết hợp 
thể hiện thông qua các đồ thị hình 1 và 
hình 2. 
Hình 1: Đồ thị khảo sát sự phụ thuộc của R(2,2) theo biên độ r, k = 1 ứng với 
 đường (3), k = 1,5 ứng với đường (1) và k = 2 ứng với đường (2) 
(1) 
(2) 
(3) 
TẠP CHÍ KHOA HỌC - ĐẠI HỌC ĐỒNG NAI, SỐ 13 - 2019 ISSN 2354-1482 
120 
Hình 2: Đồ thị khảo sát sự phụ thuộc của R(3,3) theo biên độ r, k = 1 ứng với 
đường (3), k = 1,5 ứng với đường (1) và k = 2 ứng với đường (2) 
Từ đồ thị hình 1 và hình 2 ta thấy 
với cùng điều kiện đã chọn thì giá trị 
của tham số R luôn có giá trị âm, tức là 
trạng thái thêm và bớt một photon lên 
hai mode kết hợp hoàn toàn đan rối theo 
tiêu chuẩn Hillery Zubairy bậc cao. Đặc 
biệt khi r càng tăng thì R càng âm, 
nghĩa là tính đan rối xảy ra càng mạnh. 
2.2. Định lượng độ rối bằng tiêu 
chuẩn Entropy tuyến tính 
Tiêu chuẩn Entropy tuyến tính của 
Agarwal và Bisw