Điều khiển hệ pendubot sử dụng dạng toàn phương tuyến tính dựa trên logic mờ
Pendubot được nghiên cứu trong đề tài bao
gồm 2 thanh đồng chất, đầu 1 được gắn chặt vào
động cơ DC. Đầu cuối thanh được gắn vào đầu
thanh 2 sao cho thanh 2 quay tự do xung quanh
thanh nối với thanh 1. Mô hình Pendubot được
ứng dụng trong rất nhiều phòng Thí nghiệm
nhằm nghiên cứu các giải thuật điều khiển thông
minh, điều khiển hiện đại.
Tác giả Cao Văn Kiên trong bài báo (năm
2016) [1] nghiên cứu giải thuật trượt để Swingup
và cân bằng hai thanh của hệ thống Pendubot tại
vị trí TOP. Tác giả Phan Việt Hùng trong [5]
nghiên cứu bộ điều khiển Swingup và Balancing
sử dụng phương pháp PID, LQR để ổn định hệ
thống Pendubot tại vị trí TOP. Tác giả mong
muốn thiết kế giải thuật Fuzzy-LQR lên hệ
Pendubot để kiểm chứng bộ điều khiển.
Ở bài báo này, nhóm tác giả sẽ đề cập đến
phương pháp điều khiển Fuzzy-LQR để điều
khiển vị trí TOP cho hệ pendubot. Đầu tiên, tác
giả thiết kế mô hình toán học của hệ thống lên
Matlab/ Simuthanh kết hợp với bộ điều khiển
LQR để tìm ra các thông số K để điều khiển
Pendubot ổn định. Sau đó, lấy thông số K để tính
toán các E (lỗi) và EC (tỉ lệ lỗi) và tiếp tục đưa
vào mô phỏng Matlab/Simuthanh kết hợp giải
thuật di truyền (GA) [4] và giải thuật Fuzzy để
tìm ra các thống số của bộ tiền xử lý và hậu xử lý
cho hệ thống.

Trang 1

Trang 2
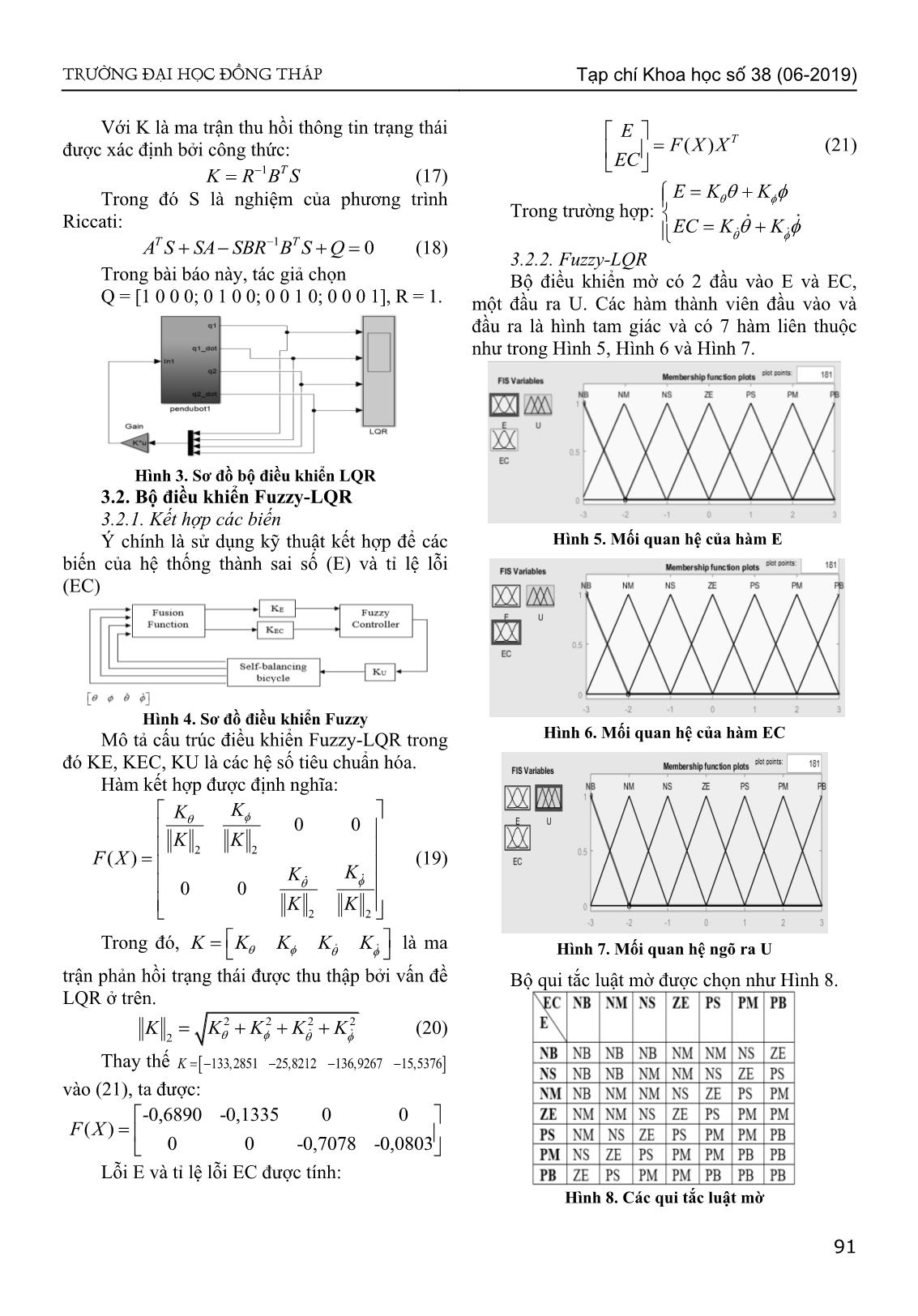
Trang 3
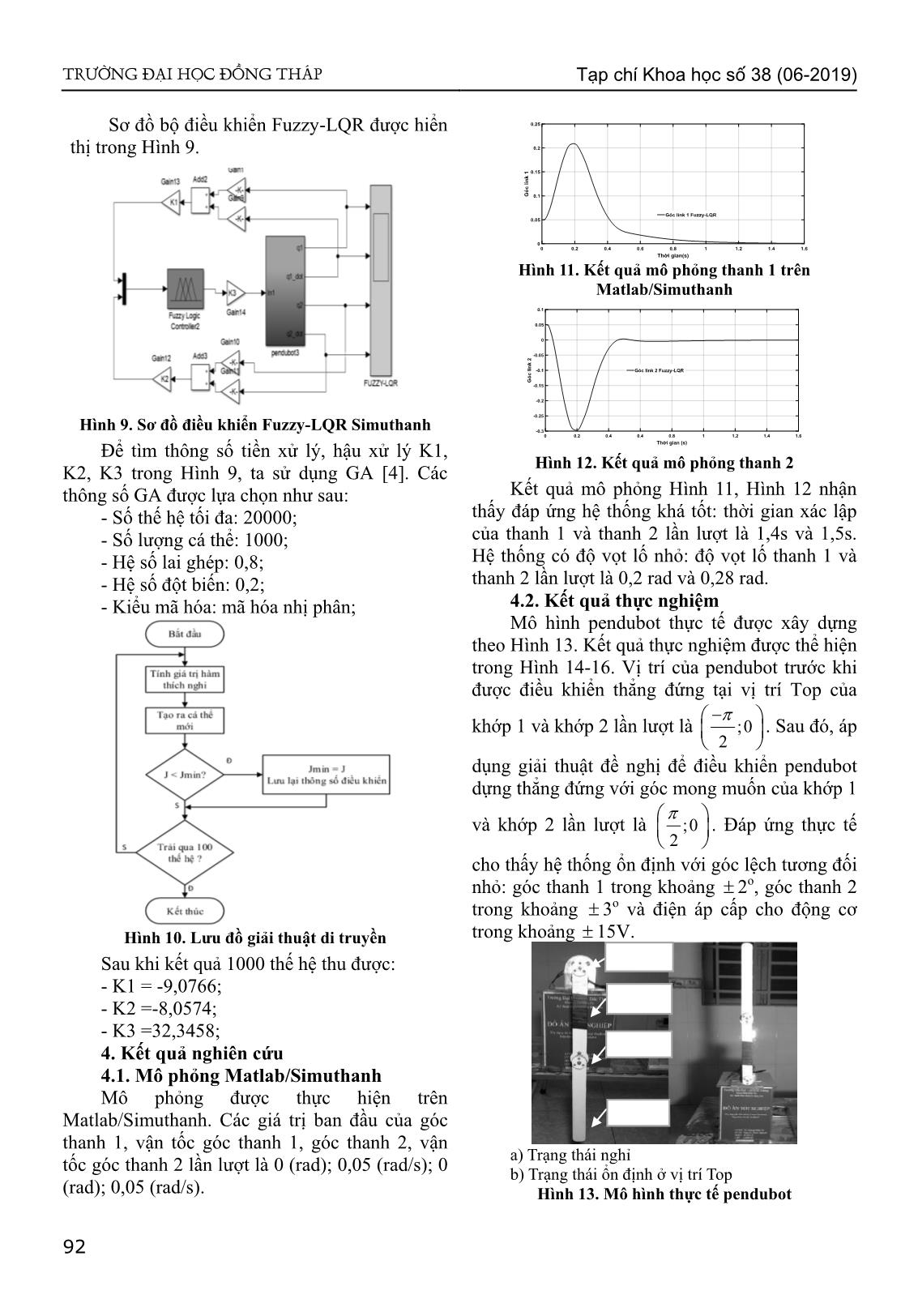
Trang 4
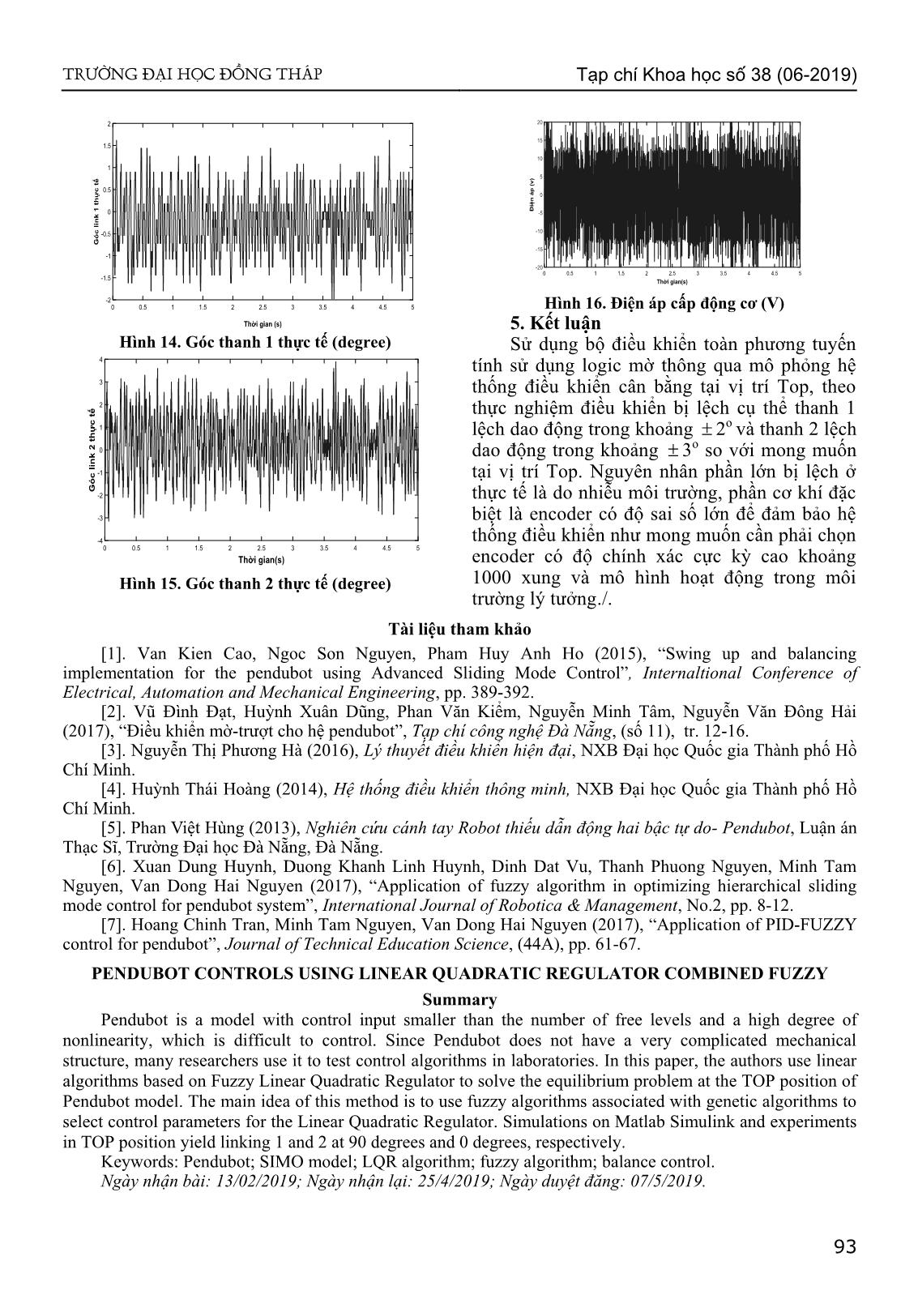
Trang 5
Tóm tắt nội dung tài liệu: Điều khiển hệ pendubot sử dụng dạng toàn phương tuyến tính dựa trên logic mờ

TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 38 (06-2019) ĐIỀU KHIỂN HỆ PENDUBOT SỬ DỤNG DẠNG TOÀN PHƢƠNG TUYẾN TÍNH DỰA TRÊN LOGIC MỜ Nguyeãn Thaønh Nguyeân(*), Nguyeãn Phong Löu(**), Nguyeãn Vaên Ñoâng Haûi(**) Toùm taét Mô hình Pendubot là mô hình có ngõ vào điều khiển ít hơn số bậc tự do, có độ phi tuyến cao và rất khó để điều khiển. Pendubot với cấu trúc cơ khí không quá phức tạp nên được nhiều nhà nghiên cứu sử dụng để kiểm tra giải thuật điều khiển trong các phòng thí nghiệm. Trong bài báo này, tác giả sử dụng giải thuật toàn phương tuyến tính dựa trên logic mờ (Fuzzy Linear Quadratic Regulator) để giải quyết bài toán cân bằng tại vị trí TOP của mô hình Pendubot. Ý tưởng chính của phương pháp này là sử dụng giải thuật mờ kết hợp với giải thuật di truyền để lựa chọn thông số điều khiển cho bộ điều khiển tuyến tính bậc hai (Linear Quadratic Regulator). Thông qua mô phỏng trên Matlab/Simulink và thực nghiệm điều khiển tại vị trí TOP với thanh 1 và thanh 2 lần lượt tại 90 độ và 0 độ. Từ khóa: Pendubot, mô hình SIMO, giải thuật LQR, giải thuật mờ, điều khiển cân bằng. 1. Giới thiệu 2. Phƣơng trình động lực học Pendubot được nghiên cứu trong đề tài bao Theo [6], ta có cấu trúc của mô hình gồm 2 thanh đồng chất, đầu 1 được gắn chặt vào pendubot như Hình 1. Thông số của hệ thống động cơ DC. Đầu cuối thanh được gắn vào đầu được thể hiện ở Bảng 1. thanh 2 sao cho thanh 2 quay tự do xung quanh Bảng 1. Thông số hệ thống thanh nối với thanh 1. Mô hình Pendubot được Ký ứng dụng trong rất nhiều phòng Thí nghiệm Đơn vị Mô tả nhằm nghiên cứu các giải thuật điều khiển thông hiệu Mô-men quán tính minh, điều khiển hiện đại. I1 kg.m2 Tác giả Cao Văn Kiên trong bài báo (năm thanh 1 2016) [1] nghiên cứu giải thuật trượt để Swingup Mô-men quán tính I2 kg.m2 và cân bằng hai thanh của hệ thống Pendubot tại thanh 2 vị trí TOP. Tác giả Phan Việt Hùng trong [5] m2 kg Khối lượng thanh 2 nghiên cứu bộ điều khiển Swingup và Balancing l m Chiều dài thanh 2 sử dụng phương pháp PID, LQR để ổn định hệ 2 thống Pendubot tại vị trí TOP. Tác giả mong Khoảng cách từ muốn thiết kế giải thuật Fuzzy-LQR lên hệ lc2 m trục encoder đến Pendubot để kiểm chứng bộ điều khiển. trọng tâm thanh 2 Ở bài báo này, nhóm tác giả sẽ đề cập đến m1 kg Khối lượng thanh 1 phương pháp điều khiển Fuzzy-LQR để điều l1 m Chiều dài thanh 1 khiển vị trí TOP cho hệ pendubot. Đầu tiên, tác Khoảng cách trục giả thiết kế mô hình toán học của hệ thống lên lc1 m động cơ đến trong Matlab/ Simuthanh kết hợp với bộ điều khiển tâm thanh 1 LQR để tìm ra các thông số K để điều khiển Gia tốc trọng Pendubot ổn định. Sau đó, lấy thông số K để tính G m/s2 trường toán các E (lỗi) và EC (tỉ lệ lỗi) và tiếp tục đưa vào mô phỏng Matlab/Simuthanh kết hợp giải Kt Nm/A Hằng số mô-men thuật di truyền (GA) [4] và giải thuật Fuzzy để Kb V/(rad/s) Hằng số phản điện tìm ra các thống số của bộ tiền xử lý và hậu xử lý Rm Ohm Điện trở động cơ cho hệ thống. Mô-men quan tính Jm Kg.m 2 rotor (*) Sinh viên, Trường Đại học Tôn Đức Thắng. (**) Trường Đại học Sư phạm Kỹ thuật Thành phố Cm Nm/(rad/s) Hệ số ma sát nhớt Hồ Chí Minh. 89 TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 38 (06-2019) sin(x )( x x )2 2 sin( x )cos( x ) x 2 2 3 3 2 4 3 3 3 2 24 gcos( x 135 ) g cos( x 3 )cos( x 13 x ) K 222 x 21K bx1() 22 (11) Kx3 2 1 2 3cos ( 3 ) 1 fx1(). 22 (12) Kx3 2 1 2 3cos ( 3 ) Hình 1. Cấu trúc của mô hình pendubot ( sin(x )( sin( x ))( x x ))2 Dùng phương pháp Euler-Lagrange [5], ta 3 3 2 3 3 2 4 2 có phương trình động lực học của hệ thống 3sin(x 3 )( 1 3 cos( x 3 )) x 2 pendubot như sau: gcos( x )( cos( x )) M()(,)() q q B q q q G q (1) 2 4 1 2 3 3 g( K cos( x ))cos( x x ) T 5 3 1 3 3 1 3 với q q12 q , q1 là góc giữa thanh 1 và trục 2 K2( 2 3 cos( x 3 )) x 2 K 3 3 x 2 sin( x 3 ) hoành (Ox), q là góc giữa thanh 1 và thanh 2, 2 cos(xK ) T bx() 2 3 3 1 (13) 0 là tín hiệu điều khiển, mô-men của 2 22 m Kx3 2 1 2 3cos ( 3 ) động cơ đặt vào thanh 1; 1 2 2 3 cos(qq 2 ) 2 3 cos( 2 ) Mq() (2) 2 3cos(q 2 ) 2 3sin(q 2 ) q 2 3 sin( q 2 ) q 2 3 sin( q 2 ) q 1 B(,) q q (3) 3sin(qq 2 ) 1 0 4gcos( q 1 ) 5 g cos( q 1 q 2 ) Gq() (4) Hình 2. Vị trí cân bằng pendubot 5gcos( q 1 q 2 ) Hai vị trí cân bằng pendubot [6] phổ biến 22 2 trong việc điều khiển hệ pendubot là vị trí TOP 1 m 1 lc 1 m 2 l 1 I 1; 2 m 2 lc 2 I 2; m l l ; m l m l ; ml . và vị trí MID như trong Hình 2. Trong bài báo 3 2 1c 2 4 1c 1 2 1 5 2c 2 này, nhóm tác giả điều khiển pendubot tại vị trí Do tín hiệu điều khiển của hệ thống T TOP. Ta đặt biến trạng thái mới XXXXX pendubot trong thực tế là điện áp cấp cho động 1 2 3 4 T cơ nên việc tìm mối liên quan giữa mô-men và để thay thế x x1 x 2 x 3 x 4 . Mục đích là điện áp là cần thiết. Theo [7] và qua một số phép để lái biến trạng thái X về 0 khi hệ thống ổn biến đổi đơn giản, ta có được phương trình sau: định. Theo hệ trục tọa độ như Hình 1, X sẽ được KKK tu t b C q J q (5) m m m 1 đặt như sau: Xx11 ; Xx22 ; Xx33 ; RRmm 2 Kt KKtb Đặt K ; KC ; KJ ; Xx44 . Thay xX11 ; xX22 ; xX33 ; 1 R 2 R m 3 m 2 m m xX vào fx(), bx(), fx(), bx() ta được xq ; xq ; xq ; xq ; 44 1 1 2 2 11213242 fX(), bX(), fX(). Kết hợp với (1), ta được: 1 1 2 3. Giải thuật điều khiển xx (6) 12 3.1. Giải thuật LQR (7) x2 f 1()() x b 1 x u Phương trình trạng thái: xx34 (8) x Ax Bu (14) x f()() x b x u (9) 1 4 2 2 J () xTT Qx u Ru dt (15) với: 2 0 1 fx1(). 22 (10) u()() t Kx t (16) Kx3 2 1 2 3cos ( 3 ) 90 TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 38 (06-2019) Với K là ma trận thu hồi thông tin trạng thái E T được xác định bởi công thức: FXX() (21) EC KRBS 1 T (17) Trong đó S là nghiệm của phương trình EKK Trong trường hợp: Riccati: EC K K ATT S SA SBR 1 B S Q 0 (18) 3.2.2. Fuzzy-LQR Trong bài báo này, tác giả chọn Bộ điều khiển mờ có 2 đầu vào E và EC, Q = [1 0 0 0; 0 1 0 0; 0 0 1 0; 0 0 0 1], R = 1. một đầu ra U. Các hàm thành viên đầu vào và đầu ra là hình tam giác và có 7 hàm liên thuộc như trong Hình 5, Hình 6 và Hình 7. Hình 3. Sơ đồ bộ điều khiển LQR 3.2. Bộ điều khiển Fuzzy-LQR 3.2.1. Kết hợp các biến Ý chính là sử dụng kỹ thuật kết hợp để các Hình 5. Mối quan hệ của hàm E biến của hệ thống thành sai số (E) và tỉ lệ lỗi (EC) Hình 4. Sơ đồ điều khiển Fuzzy Mô tả cấu trúc điều khiển Fuzzy-LQR trong Hình 6. Mối quan hệ của hàm EC đó KE, KEC, KU là các hệ số tiêu chuẩn hóa. Hàm kết hợp được định nghĩa: K K 00 KK 22 FX() (19) K K 00 KK 22 Trong đó, KKKKK là ma Hình 7. Mối quan hệ ngõ ra U trận phản hồi trạng thái được thu thập bởi vấn đề Bộ qui tắc luật mờ được chọn như Hình 8. LQR ở trên. KKKKK 2222 (20) 2 Thay thế K 133,2851 25,8212 136,9267 15,5376 vào (21), ta được: -0,6890 -0,1335 0 0 FX() 0 0 -0,7078 -0,0803 Lỗi E và tỉ lệ lỗi EC được tính: Hình 8. Các qui tắc luật mờ 91 TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 38 (06-2019) Sơ đồ bộ điều khiển Fuzzy-LQR được hiển thị trong Hình 9. Hình 11. Kết quả mô phỏng thanh 1 trên Matlab/Simuthanh Hình 9. Sơ đồ điều khiển Fuzzy-LQR Simuthanh Để tìm thông số tiền xử lý, hậu xử lý K1, Hình 12. Kết quả mô phỏng thanh 2 K2, K3 trong Hình 9, ta sử dụng GA [4]. Các thông số GA được lựa chọn như sau: Kết quả mô phỏng Hình 11, Hình 12 nhận - Số thế hệ tối đa: 20000; thấy đáp ứng hệ thống khá tốt: thời gian xác lập - Số lượng cá thể: 1000; của thanh 1 và thanh 2 lần lượt là 1,4s và 1,5s. - Hệ số lai ghép: 0,8; Hệ thống có độ vọt lố nhỏ: độ vọt lố thanh 1 và - Hệ số đột biến: 0,2; thanh 2 lần lượt là 0,2 rad và 0,28 rad. - Kiểu mã hóa: mã hóa nhị phân; 4.2. Kết quả thực nghiệm Mô hình pendubot thực tế được xây dựng theo Hình 13. Kết quả thực nghiệm được thể hiện trong Hình 14-16. Vị trí của pendubot trước khi được điều khiển thẳng đứng tại vị trí Top của khớp 1 và khớp 2 lần lượt là ;0 . Sau đó, áp 2 dụng giải thuật đề nghị để điều khiển pendubot dựng thẳng đứng với góc mong muốn của khớp 1 và khớp 2 lần lượt là ;0 . Đáp ứng thực tế 2 cho thấy hệ thống ổn định với góc lệch tương đối nhỏ: góc thanh 1 trong khoảng 2o, góc thanh 2 trong khoảng 3o và điện áp cấp cho động cơ Hình 10. Lƣu đồ giải thuật di truyền trong khoảng 15V. Sau khi kết quả 1000 thế hệ thu được: - K1 = -9,0766; - K2 =-8,0574; - K3 =32,3458; 4. Kết quả nghiên cứu 4.1. Mô phỏng Matlab/Simuthanh Mô phỏng được thực hiện trên Matlab/Simuthanh. Các giá trị ban đầu của góc thanh 1, vận tốc góc thanh 1, góc thanh 2, vận a) Trạng thái nghỉ tốc góc thanh 2 lần lượt là 0 (rad); 0,05 (rad/s); 0 b) Trạng thái ổn định ở vị trí Top (rad); 0,05 (rad/s). Hình 13. Mô hình thực tế pendubot 92 TRÖÔØNG ÑAÏI HOÏC ÑOÀNG THAÙP Taïp chí Khoa hoïc soá 38 (06-2019) Hình 16. Điện áp cấp động cơ (V) 5. Kết luận Hình 14. Góc thanh 1 thực tế (degree) Sử dụng bộ điều khiển toàn phương tuyến tính sử dụng logic mờ thông qua mô phỏng hệ thống điều khiển cân bằng tại vị trí Top, theo thực nghiệm điều khiển bị lệch cụ thể thanh 1 lệch dao động trong khoảng 2o và thanh 2 lệch dao động trong khoảng 3o so với mong muốn tại vị trí Top. Nguyên nhân phần lớn bị lệch ở thực tế là do nhiễu môi trường, phần cơ khí đặc biệt là encoder có độ sai số lớn để đảm bảo hệ thống điều khiển như mong muốn cần phải chọn encoder có độ chính xác cực kỳ cao khoảng Hình 15. Góc thanh 2 thực tế (degree) 1000 xung và mô hình hoạt động trong môi trường lý tưởng./. Tài liệu tham khảo [1]. Van Kien Cao, Ngoc Son Nguyen, Pham Huy Anh Ho (2015), “Swing up and balancing implementation for the pendubot using Advanced Sliding Mode Control”, Internaltional Conference of Electrical, Automation and Mechanical Engineering, pp. 389-392. [2]. Vũ Đình Đạt, Huỳnh Xuân Dũng, Phan Văn Kiểm, Nguyễn Minh Tâm, Nguyễn Văn Đông Hải (2017), “Điều khiển mờ-trượt cho hệ pendubot”, Tạp chí công nghệ Đà Nẵng, (số 11), tr. 12-16. [3]. Nguyễn Thị Phương Hà (2016), Lý thuyết điều khiển hiện đại, NXB Đại học Quốc gia Thành phố Hồ Chí Minh. [4]. Huỳnh Thái Hoàng (2014), Hệ thống điều khiển thông minh, NXB Đại học Quốc gia Thành phố Hồ Chí Minh. [5]. Phan Việt Hùng (2013), Nghiên cứu cánh tay Robot thiếu dẫn động hai bậc tự do- Pendubot, Luận án Thạc Sĩ, Trường Đại học Đà Nẵng, Đà Nẵng. [6]. Xuan Dung Huynh, Duong Khanh Linh Huynh, Dinh Dat Vu, Thanh Phuong Nguyen, Minh Tam Nguyen, Van Dong Hai Nguyen (2017), “Application of fuzzy algorithm in optimizing hierarchical sliding mode control for pendubot system”, International Journal of Robotica & Management, No.2, pp. 8-12. [7]. Hoang Chinh Tran, Minh Tam Nguyen, Van Dong Hai Nguyen (2017), “Application of PID-FUZZY control for pendubot”, Journal of Technical Education Science, (44A), pp. 61-67. PENDUBOT CONTROLS USING LINEAR QUADRATIC REGULATOR COMBINED FUZZY Summary Pendubot is a model with control input smaller than the number of free levels and a high degree of nonlinearity, which is difficult to control. Since Pendubot does not have a very complicated mechanical structure, many researchers use it to test control algorithms in laboratories. In this paper, the authors use linear algorithms based on Fuzzy Linear Quadratic Regulator to solve the equilibrium problem at the TOP position of Pendubot model. The main idea of this method is to use fuzzy algorithms associated with genetic algorithms to select control parameters for the Linear Quadratic Regulator. Simulations on Matlab Simulink and experiments in TOP position yield linking 1 and 2 at 90 degrees and 0 degrees, respectively. Keywords: Pendubot; SIMO model; LQR algorithm; fuzzy algorithm; balance control. Ngày nhận bài: 13/02/2019; Ngày nhận lại: 25/4/2019; Ngày duyệt đăng: 07/5/2019. 93
File đính kèm:
 dieu_khien_he_pendubot_su_dung_dang_toan_phuong_tuyen_tinh_d.pdf
dieu_khien_he_pendubot_su_dung_dang_toan_phuong_tuyen_tinh_d.pdf

