Determined absorption coefficient of 85Rb atom in the y-configuration

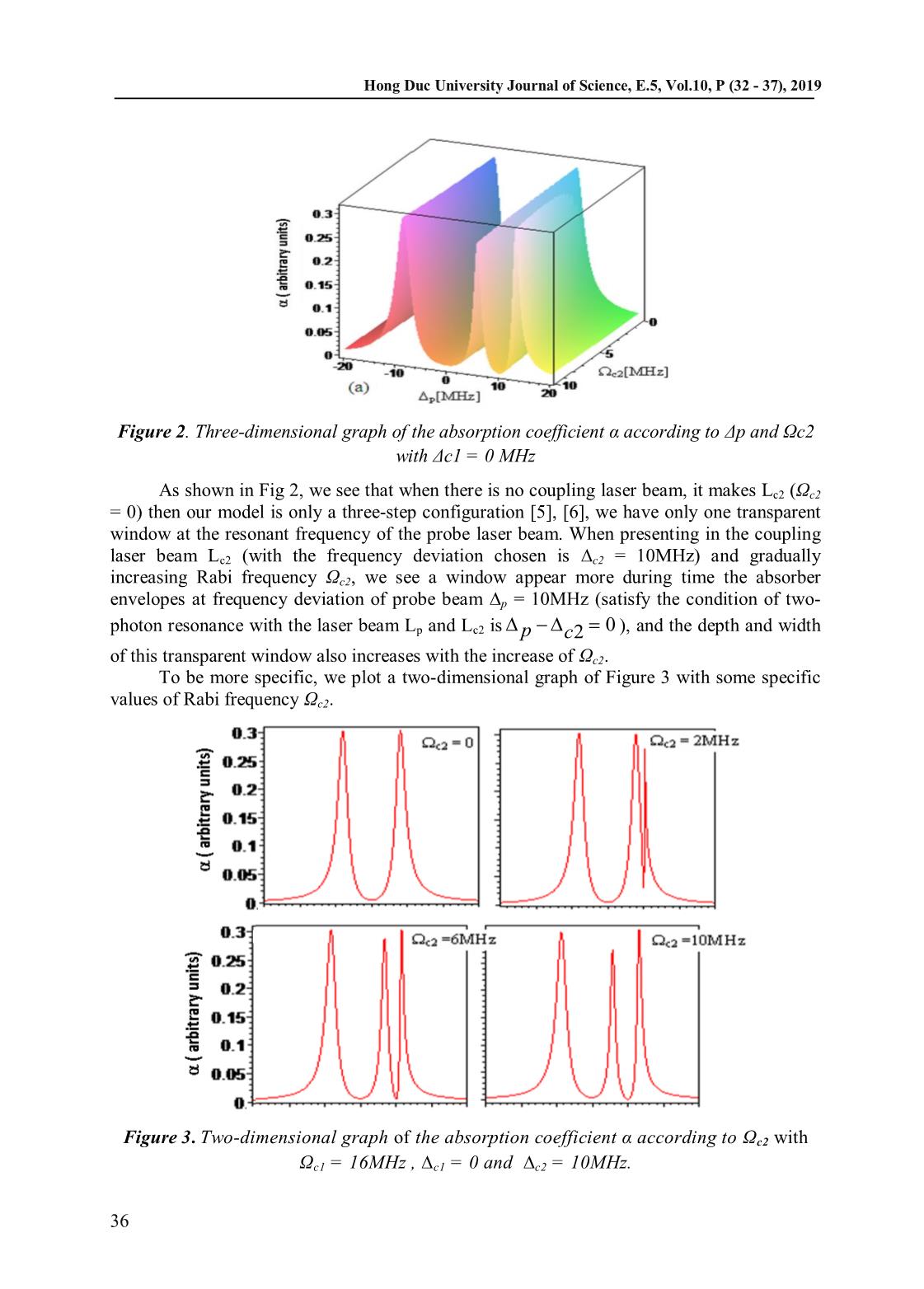
 Hong Duc University Journal of Science, E.5, Vol.10, P (32 - 37), 2019 
DETERMINED ABSORPTION COEFFICIENT OF 85Rb ATOM IN 
THE Y-CONFIGURATION ofFac. Grad. Studies, Mahidol Univ. M.M. (International Hospitality Management) / 
Nguyen Tien Dung1 
Received: 12 May 2019/ Accepted: 11 June 2019/ Published: June 2019 
©Hong Duc University (HDU) and Hong Duc University Journal of Science 
Abstract: In this work, we establish a system of equations of density and derive analytical 
expression for the absorption coefficient of 85Rb atomin the Y -configuration for a weak probe laser 
beam induced by two strong coupling laser beams. Our results show possible ways to control 
absorption coefficient by frequency detuning probe laser and intensity of the coupling laser. 
Keywords: Electromagnetically induced transparency, absorption coefficient. 
1. Introduction 
 The manipulation of subluminal and superluminal light propagation in optical medium 
has attracted many attentions due to its potential applications during the last decades, such as 
controllable optical delay lines, optical switching [2], telecommunication, interferometry, 
optical data storage and optical memories quantum information processing, and so on [6]. 
The most important key to manipulate subluminal and superluminal light propagations lies in 
its ability to control the absorption and dispersion properties of a medium by a laser field. 
 As we know that coherent interaction between atom and light field can lead to 
interesting quantum interference effects such as electromagnetically induced transparency 
(EIT) [1]. The EIT is a quantum interference effect between the probability amplitudes that 
leads to a reduction of resonant absorption for a weak probe light field propagating through a 
medium induced by a strong coupling light field [5]. Basic configurations of the EIT effect 32
are three-level atomic systems including the -Ladder and V-type configurations. In each 
configuration, the EIT efficiency is different, in which the -type configuration is the best, 
whereas the V-type configuration is the worst [4], [7], therefore, the manipulation of light in 
each configuration are also different. This suggests that we choose to use the analytical model 
to determine the absorption coefficient for the Y configuration of the 85Rb atomic system. 
2. The density matrix equation for 85Rb atomic system configure Y 
 We first consider a Y-configuration of 85Rb atom as shown in Fig. 1. State 1 is the 
ground states of the level 5S1/2 (F=3). The 2 , 3 and 4 states are excited states of the 
levels 5P3/2 (F‟=3), 5D5/2 (F”=4) and 5D5/2 (F”=3) [7]. 
Nguyen Tien Dung 
Department of Engineering and Technology, Vinh University 
Email: Tiendungunivinh@gmail.com ( ) 
32 
 Hong Duc University Journal of Science, E.5, Vol.10, P (32 - 37), 2019 
 Fac. ofFac. Grad. Studies, Mahidol 
 Univ.M.M. (International Hospitality Management) / 
 Figure 1. Four-level excitation of the Y- configuration. 
 Put this Y-configuration into three laser beams atomic frequency and intensity 
appropriate: a week probe laser Lp has intensity Ep with frequency p applies the transition 
 42Ep
 2  4 and the Rabi frequencies of the probe  p ; Two strong coupling laser 
Lc1 and Lc2 couple the transition 1  2 and  3 the Rabi frequencies of the two 
 21Ec 1 32Ec 2
coupling fields  c1 and  c2 , where ij is the electric dipole matrix 
element i  j . The evolution of the system, which is represented via the density 
operator is determined by the following Liouville equation [2]: 
  i
 H,   , (1) 
 t
where, H represents the total Hamiltonian and Λ represents the decay part. Hamilton of 33
the systerm can be written by matrix form: 
 c1 itc1
 1 e 00
 2
 
 cc12 icc12 t i t p itp
 e2 e e
 H 2 2 2 (2) 
  it
 00c2 e c2 
 2 3
  p itp
 00e 
 2 4
 it()p c2
 We consider the slow variation and put: 43 43e , 
 it it
 p p c1 itc2 it cc12 
 42 42e , 41 41e , 32 32e , 31 31e
 itc1
, 21 21e . In the framework of the semiclassical theory, the density matrix 
equations can be written as: 
 33 
 Hong Duc University Journal of Science, E.5, Vol.10, P (32 - 37), 2019 
 i p (3.1) 
  
 442 42 24 43 44 ofFac. Grad. Studies, Mahidol Univ. M.M. (International Hospitality Management) / 
 (3.2) 
 ic1 i p
 [()]i p  
 4122 42 21c 1 41 41
 (3.3) 
 iicc12i p
 ()() i p  
 422 41 2 43 2 44 22 42 42
 (3.4) 
 ic2 i p
 [()]i p  
 4322 42 23c 2 43 43
 i (3.5) 
 c2   
 332 32 23 43 44 32 33
 iicc12 (3.6) 
 [()]i p  
 3122 32 21c 1 31 31
 ii i p (3.7) 
 cc12 ()i  
 322 31 2 33 22 2 34c 2 32 32
 (3.8) 
 i p ic2
 [()] i p  
 3422 32 24c 2 43 34
 iiip (3.9) 
 cc12   
 222 21 12 2 23 32 2 24 42 32 33 21 22
 iii p (3.10) 
 cc12 ()i  
 212 22 11 2 31 2 41c 1 21 21
 iii p (3.11) 
 cc21 () i  
 232 22 33 2 13 2 43c 2 32 23
 i (3.12) 34
 p iicc12 
 ()() i p  
 242 22 44 2 14 2 34 42 24
 i (3.13) 
 c1  
 112 12 21 21 22
 iii p (3.14) 
 cc12 ()i  
 122 11 22 2 13 2 14c 1 21 12
 ii (3.15) 
 cc21 [()] i  
 1322 12 23cc 1 2 31 13
 (3.16) 
 i p ic1
 [()] i p  
 1422 12 24c 1 41 14
(where, the frequency detuning of the probe and Lc1, Lc2 coupling lasers from the relevant atomic 
transitions are respectively determined by pp  42 , cc1  1 21. In addition, 
suppose the initial atomic system is at a level 2 therefore: 11 33 44 0, 22 1. 
34 
 Hong Duc University Journal of Science, E.5, Vol.10, P (32 - 37), 2019 
 Now, we analytically solve the density matrix equations under the steady-state 
condition by setting the time derivatives to zero: 
 Fac. ofFac. Grad. Studies, Mahidol 
 d
 0 , (4) 
 dt
 Therefore the equations (3.2), (3.3) and (3.4), we have: 
 (5.1) 
 ic1 i p
 0 [i ( p )  ] 
 2242 21c 1 41 41
 (5.2) 
 iicc12i p
 0 ( ) (i p  ) 
 241 2 43 2 44 22 42 42
 (5.3) 
 i i 
 c2 p Univ.M.M. (International Hospitality Management) / 
 0 [i ( p )  ] 
 2242 23c 2 43 43
 i p i p
 Because of p << c1 and c2 so that we ignore the term and in 
 2 21 2 23
the equations (4) and (5). Slove the equations (4) – (5), we have: 
 i p /2
 , (6) 
 42 22
 cc12/ 4 / 4
 42 i p 
 41 ii()() pp cc 1 43 2
3. Absorption coefficient of the atomic medium 
 We start from the susceptibility of atomic medium for the probe light that is 
determined by the following relation: 
 Nd
  221  ' i  '' , (7) 
  E 21
 0 p 35
 The absorption coefficient α of the atomic medium for the probe beam is determined 
through the imaginary part of the linear susceptibility (7): 
 '' 2
  pp  2N42
 Im(42 ) (8) 
 ccp 0
 85
 We considere the case of Rb atomic: γ42 = 3MHz, γ41 = 0.3MHz and γ43 = 0.03MHz, 
 11 3 -29
the atomic density N = 10 /cm . The electric dipole matrix element is d42 = 2.54.10 Cm, 
 -12 -34
dielectric coefficient 0 = 8.85.10 F/m, ħ = 1,05.10 J.s, and frequency of probe beam p = 
 14
3.84.10 Hz. Fixed frequency Rabi of coupling laser beam Lc1 in value Ωc1 = 16MHz 
(correspond to the value that when there is no laser Lc2 then the transparency of the probe 
beam near 100%) and the frequency coincides with the frequency of the transition 12 , 
it means ∆c1 = 0. Consider the case of the frequency deviation of the coupling laser beam Lc2 
is ∆c2 = 10MHz . We plot a three-dimensional graph of the absorption coefficient α at the 
intensity of the coupling laser beam Lc2 (Rabi frequency Ωc2) and and the frequency deviation 
of the probe laser beam Lp, the result is shown in Fig 2. 
 35 
 Hong Duc University Journal of Science, E.5, Vol.10, P (32 - 37), 2019 
 Fac. ofFac. Grad. Studies, Mahidol Univ. M.M. (International Hospitality Management) / 
 Figure 2. Three-dimensional graph of the absorption coefficient α according to Δp and Ωc2 
 with Δc1 = 0 MHz 
 As shown in Fig 2, we see that when there is no coupling laser beam, it makes Lc2 (Ωc2 
= 0) then our model is only a three-step configuration [5], [6], we have only one transparent 
window at the resonant frequency of the probe laser beam. When presenting in the coupling 
laser beam Lc2 (with the frequency deviation chosen is ∆c2 = 10MHz) and gradually 
increasing Rabi frequency Ωc2, we see a window appear more during time the absorber 
envelopes at frequency deviation of probe beam ∆p = 10MHz (satisfy the condition of two-
photon resonance with the laser beam Lp and Lc2 is p c2 0 ), and the depth and width 
of this transparent window also increases with the increase of Ωc2. 
 To be more specific, we plot a two-dimensional graph of Figure 3 with some specific 
values of Rabi frequency Ωc2. 
 36
 Figure 3. Two-dimensional graph of the absorption coefficient α according to Ωc2 with 
 Ωc1 = 16MHz , ∆c1 = 0 and ∆c2 = 10MHz. 
36 
 Hong Duc University Journal of Science, E.5, Vol.10, P (32 - 37), 2019 
4. Conclusion 
 In the framework of the semi-classical theory, we have cited the density matrix ofFac. Grad. Studies, Mahidol 
equation for the 85Rb atomic system in the Y-configuration under the simultaneous effects of 
two laser probe and coupling beams. Using approximate rotational waves and approximate 
electric dipoles, we have found solutions in the form of analytic for the absorption coefficient 
of atoms when the probe beam has a small intensity compared to the coupling beams. 
Drawing the absorption coefficient expression will facilitate future research applications. 
Consequently, we investigated the absorption of the probe beam according to the intensity of 
the coupling beam c1, c2 and the deviation of the probe beam Δp. The results show that 
a Y-configuration appears two transparent windows for the probe laser beam. The depth and Univ.M.M. (International Hospitality Management) / 
width or position of these windows can be altered by changing the intensity or frequency 
deviations of the coupling laser fields. 
References 
[1] K.J. Boller, A. Imamoglu, and S.E. Harris (1991), Observation of electromagnetically 
 induced transparency, Phys. Rev. Lett. 66, 25-93. 
[2] R. W. Boyd (2009), Slow and fast light: fundamentals and applications, J. Mod. Opt. 
 56,1908-1915. 
[3] Daniel Adam Steck, 85Rb D Line Data:  
[4] L. V. Doai, D. X. Khoa, and N. H. Bang (2015), EIT enhanced self-Kerr nonlinearity 
 in the three-level lambda system under Doppler broadening, Phys. Scr. 90, 045-502. 
[5] M. Fleischhauer, I. Mamoglu, and J. P. Marangos (2005), Electromagnetically induced 
 transparency: optics in coherent media, Rev. Mod. Phys. 77, 633-673. 
[6] J. Javanainen (1992), Effect of State Superpositions Created by Spontaneous Emission 
 37
 on Laser-Driven Transitions, Europhys. Lett. 17, 407. 
[7] S. Sena, T. K. Dey, M. R. Nath and G. Gangopadhyay (2014), Comparison of 
 Electromagnetically Induced Transparency in lambda, vee and cascade three-level 
 systems, J. Mod. Opt. 62, 166-174. 
 37