Determination of the refractive index of optical ceramics by using transmission data in the mid - wave infrared region

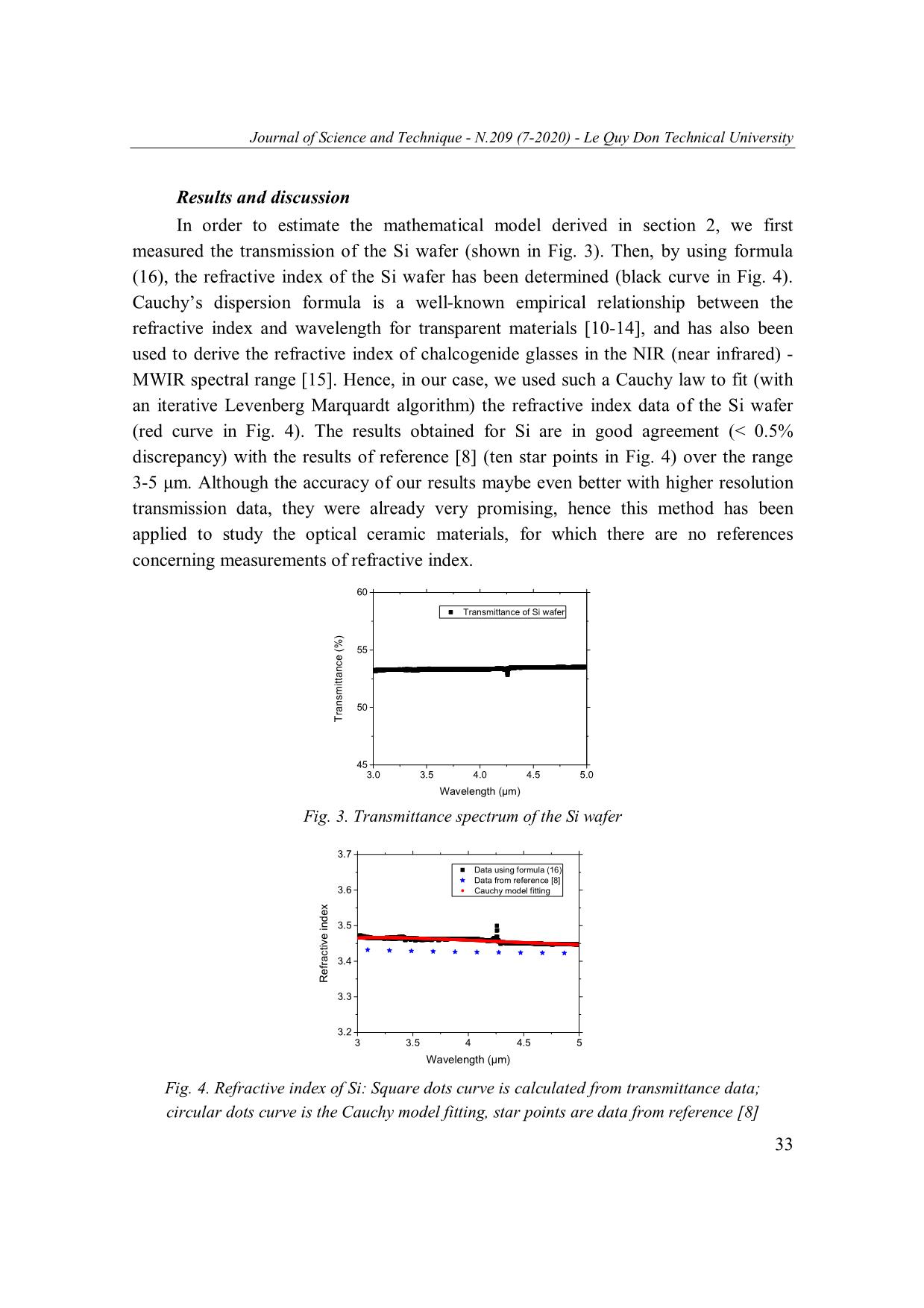
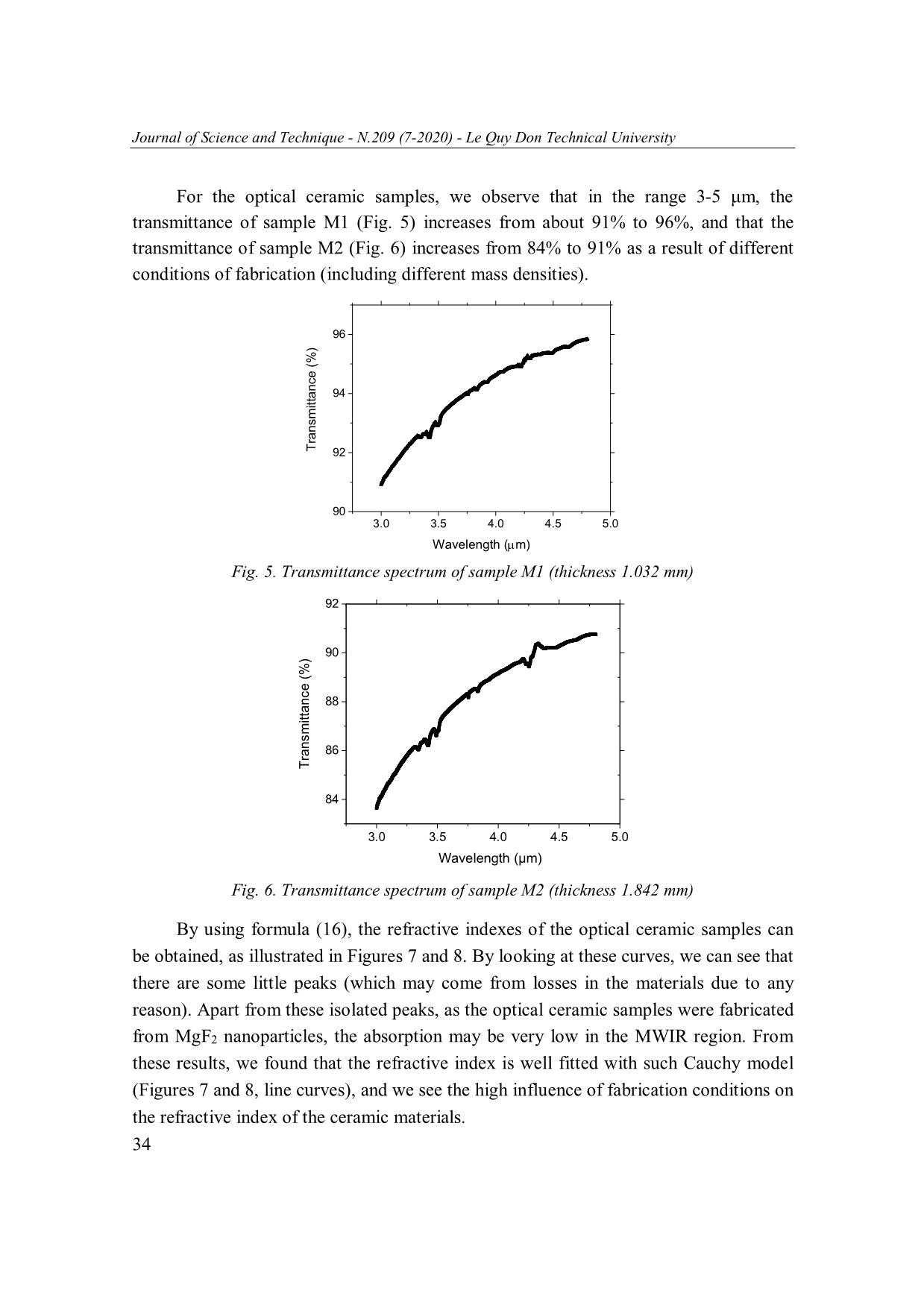
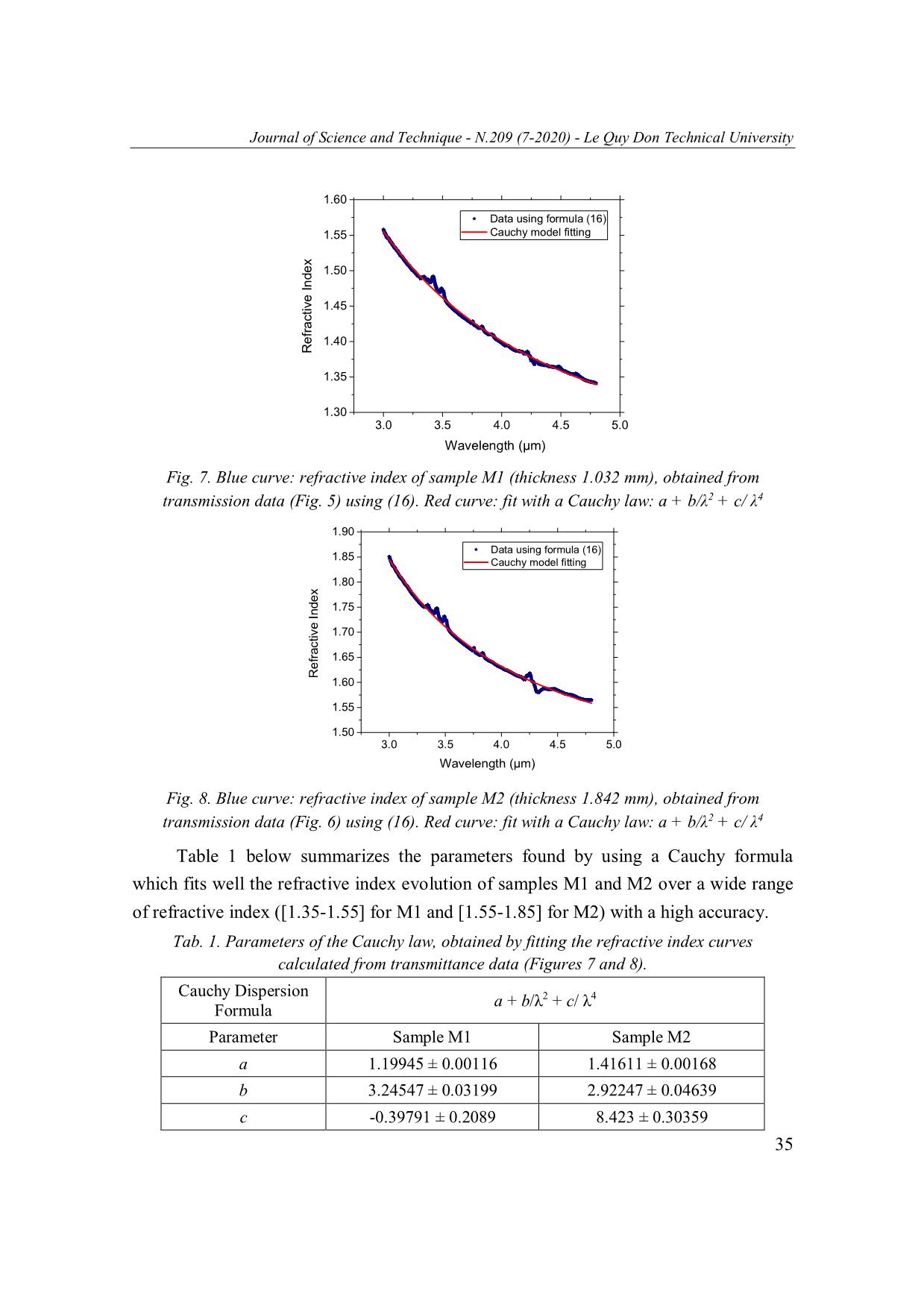
 Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
 DETERMINATION OF THE REFRACTIVE INDEX 
 OF OPTICAL CERAMICS BY USING TRANSMISSION DATA 
 IN THE MID-WAVE INFRARED REGION 
 Mai Van Huy1,*, Duong Chi Dung1, Le Hoang Hai1, 
 Le Duy Hoan2, Nguyen Tuan Hieu2, Olivier Schneegans3 
 1Le Quy Don Technical University; 
 2Institute of Technology, General Department of Military Industries and Manufacture; 
 3Laboratoire Génie Électrique et Électronique de Paris (GeePs) - CNRS – 
 CentraleSupélec, Sorbonne Université and Université Paris-Saclay – 
 91190 Gif-sur-Yvette, France 
 Abstract 
 Optical ceramics are emerging materials for optical devices operating in the Mid-Wave 
 Infrared (MWIR) spectral range. Thus determination of their refractive index is of huge 
 importance but is still a challenging issue. In this work, a model is delivered, which 
 highlights a simple mathematic relationship between the refractive index of an optical 
 material and its transmittance spectrum measured by Fourier Transform Infrared 
 Spectroscopy. Such model allows determining the refractive index of ceramics fabricated 
 by hot-pressing of MgF2 nanoparticles. The reliability of this method has been verified on a 
 silicon wafer taken as a reference (< 0.5%, discrepancy with data from literature on Si). Our 
 approach can be applied to a variety of promising novel optical materials being developed. 
 Keywords: Refractive index; optical ceramic; FTIR (Fourier Transform Infrared Spectroscopy). 
1. Introduction 
 In the design and fabrication of an optical system, the refractive indexes of the 
constitutive materials are important parameters to determine. Towards such a 
characterization, many methods have been proposed in the past, ranging from classical 
to newer techniques [1-4]. These can be grouped into two main categories: prism 
methods and spectral methods. Regarding the prism methods, the deflection of a beam 
entering and leaving a prism is measured. The advantage of these methods (e.g. 
measurement of deviation, or minimum deviation angle, by refractometry, for which a 
variety of different techniques have been developed historically [1]) is that an accurate 
value of refractive index can be obtained at a fixed wavelength. This implies the use of 
an expensive refractometer and the fabrication of a prism with high accuracy [1]. 
Unfortunately, these methods appear not suitable to measure the refractive index over a 
* Email: vanhuy.mai@mta.edu.vn 
 29
Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
wide range of wavelengths. Hence spectral methods using transmission and reflection 
data have increasingly been applied to determine the refractive index of materials with a 
good accuracy. In this case, however, each time a new kind of materials is studied, 
special care is required to ensure that the proposed model is in adequation with the 
experimental data [5, 6]. 
 Single-crystal magnesium fluoride (MgF2) is a positive uniaxial crystal whose 
useful optical transmission is in the range of between 0.11 and 7.5 μm [3]. An optical 
ceramic, composed of polycrystalline high density MgF2, is elaborated by a hot-pressing 
technique; in the MWIR, its high transmittance interval lies in the range 2.5 to 6 μm [7]. 
This material has been widely used in the field of optics, especially for missiles domes. 
By traditional methods, the refractive index of this material is difficult to determine in 
the MWIR. In this paper, we first present the calculation and experiments carried out to 
determine the refractive index of a Si substrate by using FTIR. Our results were in good 
agreement (< 0.5% discrepancy) with published results in the 3-5 μm spectral range [8], 
hence we then applied this method to determine the refractive index of an optical 
ceramic, using parallel plate samples. 
2. Methods and Experiments 
 Mathematical model for calculation of refractive index 
 Towards calculation of the refractive index, we first assume that a flat parallel 
plate sample has been polished on both sides (the surface roughness may thus be 
neglected), and that the sample is surrounded by ambient air (conditions to measure the 
transmission data), as illustrated in Fig. 1. The light beam reaches the sample at normal 
incidence, the sample thickness is such as both interference and absorption can 
be neglected. 
 For each interface (air/substrate and substrate/air, respectively), we denote the 
transmittance and reflectance: T1, R1 and T2, R2 respectively. For a light (of intensity I0) 
coming from the left (Fig. 1), we can calculate the intensity at each interface by using 
the following equations [9]: 
 ITI1 1 0 (1) 
 ITITTI2 2 1 1 2 0 (2) 
 IRIRTI3 2 1 2 1 0 (3) 
 IRIRRTI4 1 3 1 2 1 0 (4)
 ITITTRRI5 2 4 1 2 1 2 0 (5) 
30 
 Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
 2
 IRIRRTI6 2 4 1 2 1 0 (6) 
 2 2
 IRIRRTI7 1 6 1 2 1 0 (7) 
 2
 ITITTRRI8 2 7 1 2 1 2 0 (8) 
 IIIItot 2 5 8  (9) 
 ITTRRRRRRI 1 2 3  (10) 
 tot 1 2 1 2 1 2 1 2 0
 Since R1 and R2 are both inferior to 1, we can re-calculate: 
 2 3 1
 1 RRRRRR1 2 1 2 1 2  (11) 
 1 RR1 2
Therefore, expression (10) becomes: 
 TT1 2 
 ITIItot 0 0 (12) 
 1 RR1 2 
where the total transmittance T is: 
 TT 
 T 1 2 (13) 
 1 RR1 2
 Fig. 1. Schematics of the light transmission through a parallel plate substrate in air. 
 The light (intensity I0) comes from the left. The resulting total transmitted light (Itot) 
 depends on T1, R1, T2 and R2 
 If we assume that both sides of the sample have undergone the same polishing, then 
both interfaces (air/substrate and substrate/air) are completely symmetric, hence T1 = T2 
and R1 = R2. Besides, for a transparent sample (absorbance A = 0), we have T1 = 1 – R1. 
 31
Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
 Thus the total transmittance T of the sample can be retrieved from (13): 
 2
 (1 R1 )
 T 2 (14) 
 1 R1
where R1 is the reflectance which comes from the Fresnel equations: 
 2
 n 1 
 R1 (15) 
 n 1 
 Finally, as the transmittance T is a function of wavelength , the refractive index 
n() is obtained from the transmittance T() using (14) and (15): 
 2
 1 1 T ( )
 n() (16) 
 T ()
 Fabrication of the IR optical ceramics 
 The experiments have been carried out on two kinds of samples: 
 - A Si wafer (diameter 1 inch, thickness 2 mm, polished on both sides), with the 
objective of comparing our results with published data. This kind of wafer is almost 
used in the field of optical thin film coating. 
 - Two optical ceramic parallel plate samples which were fabricated at the Institute 
of Technology, General Department of Military Industries and Manufacture. The samples 
were fabricated by hot pressing of MgF2 nano particles (size 70-90 nm), in an annealing 
furnace at a pressure of 10-2 bar. The optical ceramic parallel plate samples M1 and M2 
have been polished on both sides (resulting roughness < 0.05 µm). Sample M1 (thickness 
1.032 mm) was annealed at a temperature of 640.9oC during 33 minutes at a pressure of 
231.4 MPa, and sample M2 (thickness 1.842 mm) has been annealed at a temperature of 
651oC during 35 minutes at a pressure of 240.5 MPa. The mass density of samples M1 
and M2 are 3.17 and 3.18 g/cm3 respectively. The transmittance of the samples was 
measured in the MWIR region by using a FTIR spectrometer “Nicolet Summit Pro” of 
Thermo Scientific. 
 Fig. 2. Optical photos of the optical ceramic samples: the thickness of M1 (left) is 1.032 mm, 
 the thickness of M2 (right) is 1.842 mm 
32 
 Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
 Results and discussion 
 In order to estimate the mathematical model derived in section 2, we first 
measured the transmission of the Si wafer (shown in Fig. 3). Then, by using formula 
(16), the refractive index of the Si wafer has been determined (black curve in Fig. 4). 
Cauchy’s dispersion formula is a well-known empirical relationship between the 
refractive index and wavelength for transparent materials [10-14], and has also been 
used to derive the refractive index of chalcogenide glasses in the NIR (near infrared) - 
MWIR spectral range [15]. Hence, in our case, we used such a Cauchy law to fit (with 
an iterative Levenberg Marquardt algorithm) the refractive index data of the Si wafer 
(red curve in Fig. 4). The results obtained for Si are in good agreement (< 0.5% 
discrepancy) with the results of reference [8] (ten star points in Fig. 4) over the range 
3-5 μm. Although the accuracy of our results maybe even better with higher resolution 
transmission data, they were already very promising, hence this method has been 
applied to study the optical ceramic materials, for which there are no references 
concerning measurements of refractive index. 
 60
 Transmittance of Si wafer
 55
 50
 Transmittance (%)
 45
 3.0 3.5 4.0 4.5 5.0
 Wavelength (µm)
 Fig. 3. Transmittance spectrum of the Si wafer 
 3.7
 Data using formula (16)
 Data from reference [8]
 3.6 Cauchy model fitting
 3.5
 3.4
 Refractive index Refractive
 3.3
 3.2
 3 3.5 4 4.5 5
 Wavelength (µm)
 Fig. 4. Refractive index of Si: Square dots curve is calculated from transmittance data; 
 circular dots curve is the Cauchy model fitting, star points are data from reference [8] 
 33
Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
 For the optical ceramic samples, we observe that in the range 3-5 μm, the 
transmittance of sample M1 (Fig. 5) increases from about 91% to 96%, and that the 
transmittance of sample M2 (Fig. 6) increases from 84% to 91% as a result of different 
conditions of fabrication (including different mass densities). 
 96
 94
 Transmittance (%) Transmittance 92
 90
 3.0 3.5 4.0 4.5 5.0
 Wavelength (m) 
 Fig. 5. Transmittance spectrum of sample M1 (thickness 1.032 mm) 
 92
 90
 88
 86
 Transmittance (%) Transmittance
 84
 3.0 3.5 4.0 4.5 5.0
 Wavelength (µm)
 Fig. 6. Transmittance spectrum of sample M2 (thickness 1.842 mm) 
 By using formula (16), the refractive indexes of the optical ceramic samples can 
be obtained, as illustrated in Figures 7 and 8. By looking at these curves, we can see that 
there are some little peaks (which may come from losses in the materials due to any 
reason). Apart from these isolated peaks, as the optical ceramic samples were fabricated 
from MgF2 nanoparticles, the absorption may be very low in the MWIR region. From 
these results, we found that the refractive index is well fitted with such Cauchy model 
(Figures 7 and 8, line curves), and we see the high influence of fabrication conditions on 
the refractive index of the ceramic materials. 
34 
 Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
 1.60
 Data using formula (16)
 1.55 Cauchy model fitting
 1.50
 1.45
 1.40
 Refractive Index Refractive
 1.35
 1.30
 3.0 3.5 4.0 4.5 5.0
 Wavelength (µm)
 Fig. 7. Blue curve: refractive index of sample M1 (thickness 1.032 mm), obtained from 
 transmission data (Fig. 5) using (16). Red curve: fit with a Cauchy law: a + b/λ2 + c/ λ4 
 1.90
 Data using formula (16)
 1.85
 Cauchy model fitting
 1.80
 1.75
 1.70
 1.65
 Refractive Index Refractive 1.60
 1.55
 1.50
 3.0 3.5 4.0 4.5 5.0
 Wavelength (µm)
 Fig. 8. Blue curve: refractive index of sample M2 (thickness 1.842 mm), obtained from 
 transmission data (Fig. 6) using (16). Red curve: fit with a Cauchy law: a + b/λ2 + c/ λ4 
 Table 1 below summarizes the parameters found by using a Cauchy formula 
which fits well the refractive index evolution of samples M1 and M2 over a wide range 
of refractive index ([1.35-1.55] for M1 and [1.55-1.85] for M2) with a high accuracy. 
 Tab. 1. Parameters of the Cauchy law, obtained by fitting the refractive index curves 
 calculated from transmittance data (Figures 7 and 8). 
 Cauchy Dispersion 
 a + b/λ2 + c/ λ4 
 Formula 
 Parameter Sample M1 Sample M2 
 a 1.19945 ± 0.00116 1.41611 ± 0.00168 
 b 3.24547 ± 0.03199 2.92247 ± 0.04639 
 c -0.39791 ± 0.2089 8.423 ± 0.30359 
 35
Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
3. Conclusion 
 In this paper, a simple method has been presented, in order to determine the 
refractive indexes of a Si wafer and two optical ceramic plates in the MWIR region, by 
use of transmission data. It has been verified that the refractive index evolution n() of the 
transparent materials are well fitted by a Cauchy dispersion formula. Based on the fact 
that this method is simple and does not require an expensive device for measurements, it 
may provide a tool in the development of fabrication technology of optical ceramics and 
in the determination of the refractive index of novel optical materials. 
References 
1.  
2. Gao, L., F. Lemarchand, and M. Lequime (2013). Refractive index determination of SiO2 
 layer in the UV/Vis/NIR range: Spectrophotometric reverse engineering on single and 
 bi-layer designs. J. Europ. Opt. Soc. Rap. Public., 8, 13010. 
3. Dodge, M. J. (1984). Refractive properties of magnesium fluoride. Applied Optics, 23(12), 
 1980-1985. 
4. Fang, Y., et al. (2019). (Invited) Methods for determining the refractive indices and thermo-optic 
 coefficients of chalcogenide glasses at MIR wavelengths. Optical Materials: X, 2, 100030. 
5. Gerstenlauer, D., et al. (2014). Determination of the refractive index of TiO2-Y2O3 ceramic 
 composites. Journal of Quantitative Spectroscopy and Radiative Transfer, 135, 44-49. 
6. Mehling H, Kuhn J, Manara J, Brandt R, Fricke J (2001). Different methods for determining the 
 refractive index of SiO2 glass in the range of 1.4-50μm. High Temp High Press, 33, 35-42. 
7. Chang, C. S., M. H. Hon, and S. J. Yang (1991). The optical properties of hot-pressed 
 magnesium fluoride and single-crystal magnesium fluoride in the 0.1 to 9.0 μm range. 
 Journal of Materials Science, 26(6), 1627-1630. 
8. Chandler-Horowitz, D. and P. M. Amirtharaj (2005). High-accuracy, midinfrared 
 (450cm−1⩽ω⩽4000cm−1) refractive index values of silicon. Journal of Applied Physics, 
 97(12), 123526. 
9. Olaf Stenzel (2016). Chapter 7 of "The Physics of Thin Film Optical Spectra: An 
 Introduction" (2nd Edition). Springer Series in Surface Sciences. 
10. Liu, J.-M. (2005). Photonic Devices. Cambridge: Cambridge University Press. 
11. G. E. Jellison Jr. and F. A. Modine (1996). Parameterization of the optical functions of 
 amorphous materials in the interband region. Appl. Phys. Lett., 69(3), 371-373. 
12. F. A. Jenkins, H. E. White (1937). Fundamentals of Optics. Tata McGraw-Hill Education. 
13. H. G. Dantanarayana (2012). Application of TLM for Optical Microresonators. PhD thesis 
 University of Nottingham, UK. 
14. https://en.wikipedia.org/wiki/Cauchy%27s_equation. 
15. Němec, P., et al. (2014). Optical properties of (GeSe2)100−x(Sb2Se3)x glasses in near- and 
 middle-infrared spectral regions. Materials Research Bulletin, 51, 176-179. 
36 
 Journal of Science and Technique - N.209 (7-2020) - Le Quy Don Technical University 
 XÁC ĐỊNH CHIẾT SUẤT CỦA VẬT LIỆU GỐM QUANG HỌC 
 TỪ PHỔ TRUYỀN QUA TRONG VÙNG HỒNG NGOẠI 
 Tóm tắt: Gốm quang học là vật liệu mang tính cấp thiết trong các thiết bị quang học làm 
việc trong vùng hồng ngoại. Việc xác định chiết suất của gốm quang học là một nhiệm vụ quan 
trọng nhưng vẫn còn nhiều khó khăn. Trong bài báo này, chúng tôi dẫn chứng một mối quan hệ 
toán học đơn giản giữa chiết suất và hệ số truyền qua, điều này cho phép xác định được chiết 
suất của gốm quang học được chế tạo bằng phương pháp ép nóng hạt nano MgF2. Độ tin cậy 
của phương pháp đã được kiểm nghiệm trên đế Si và so sánh với các kết quả công bố với độ sai 
lệch dưới 0,5%. Phương pháp tiếp cận này có thể được áp dụng cho các loại vật liệu quang học 
mới đang được phát triển. 
 Từ khóa: Chiết suất; gốm quang học; phổ hồng ngoại truyền qua Fourier. 
 Received: 14/5/2020; Revised: 22/7/2020; Accepted for publication: 28/7/2020 
  
 37