Computation of bounds elastic properties of polycrystals based on fast fourier transform method

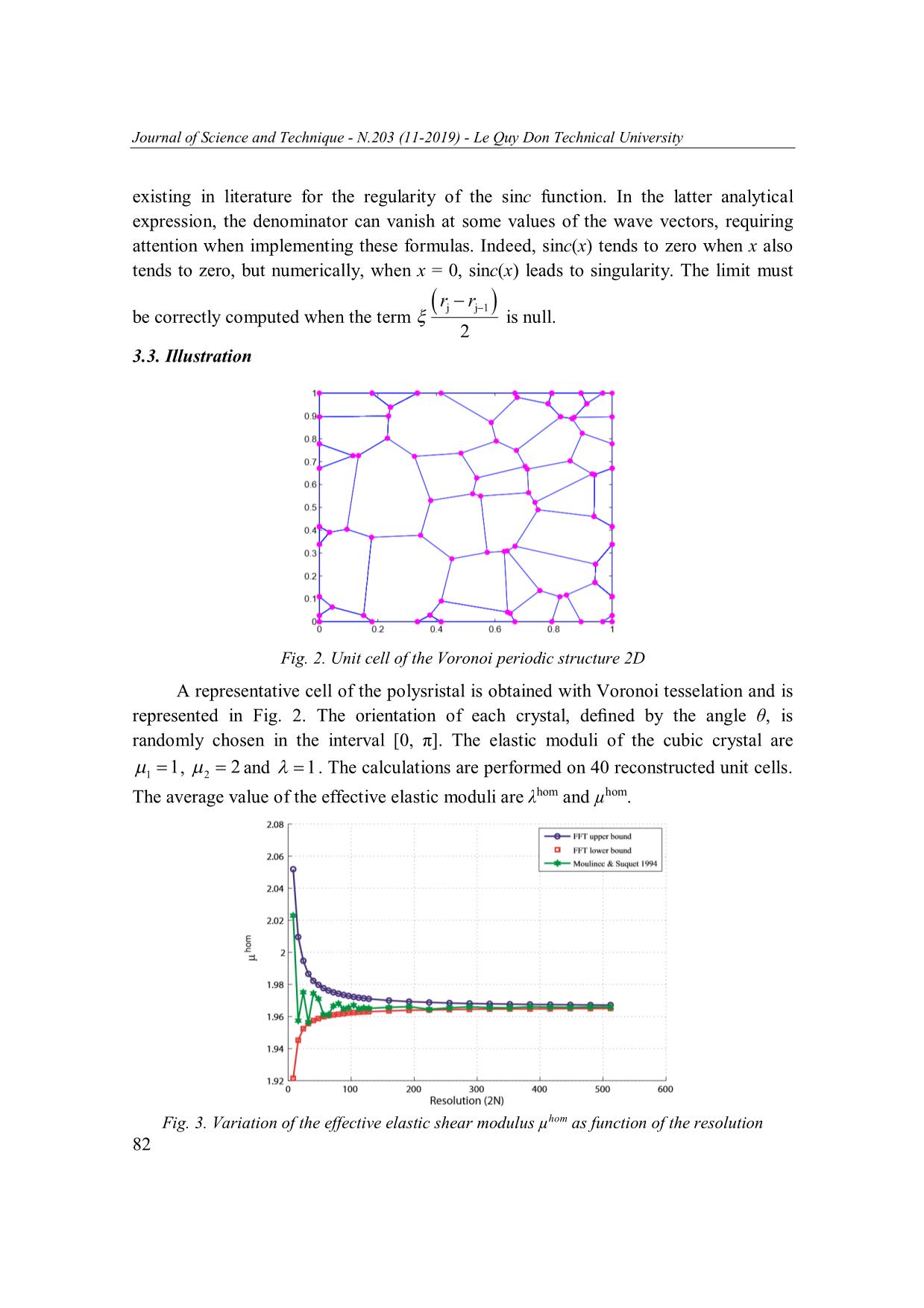
 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
 COMPUTATION OF BOUNDS ELASTIC PROPERTIES OF 
 POLYCRYSTALS BASED ON FAST FOURIER TRANSFORM METHOD 
 *
 Nguyen Minh Tan 
 Le Quy Don Technical University 
 Abstract 
 The present paper derives numerical bounds of the elastic properties of polycrystals. The 
 homogenized elastic coefficients are computed from Voronoi-type unit cells. The main 
 result of the article detemines the upper and lower bounds for a case of polycrystals made 
 up of cubic single crystals by using the fast Fourier transform method (FFT) based on the 
 shape function. Our method guarantees the exact solutions in comparison to the Moulinec 
 and Suquet’s method within some uncontrolled approximations. The proposed method 
 could be extended to account for other material symmetries such as hexagonal or tetragonal 
 crystals. 
 Keywords: Elastic coefficients; numerical bounds; shape functions; polycrystals; Voronoi; 
fast Fourier transform. 
1. Introduction 
 An alternative approach to Finite Element Method (FEM) has been proposed in the 
middle of the nineties by Moulinec and Suquet [1] for the computation of the effective 
properties of linear elastic periodic composites. The unit cell problem is solved by means 
of an iterative scheme which uses the periodic Green’s tensor for the strain and could be 
directly applied to digital images which come from microstructure. The main advantages 
of this approach over the FEM is that it does not require the introduction of a “high 
dimension” stiffness matrix. The FFT methods only need the storage of tables whose 
dimensions are the number of DoF (the FEM requires the storage of the rigidity matrix 
whose dimension is the square of the DoF). The memory needed for solving the unit cell 
problem with FFT methods is then significantly reduced. The FFT method allows to 
expand the solution of the Lippmann-Schwinger equation into Neumann series, along the 
lines of a method which was first introduced for composite conductors by Brown [2] and 
later by Kroner [3]. The convergence of the method has been largely studied in the 
literature particularly for the problems with high contrasts between the phase elastic 
properties. Other formulation has been then provided to improve the convergence: the 
(dual) stress based formulation in [4, 5] and the accelerated schemes in [6, 7, 8]. 
Accelerated schemes are not considered in the present study since the contrast in 
* Email: minhtanhvkt@gmail.com 
 73
Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
polycrystal is sufficiently low to use the basic strain and stress based iterative schemes. 
An alternative approach based on the shape functions has been developed by Bonnet [5] 
to improve the FFT solutions. The close-form expressions of the shape functions are 
available for inclusions having ellipsoidal shapes in the book of Nemat-Nasser [9], for 
instance. Later, in [10], it has been proved that the use of the shape functions in the FFT-
based iterative schemes provides rigorous bounds of the effective elastic properties of the 
composites. More precisely, the strain and stress based FFT solutions deliver an upper and 
lower bound respectively. The lower and upper bounds of the homogenized elastic 
coefficients are computed by means of the FFT method combined with the use of the 
shape functions. The microstructure of the polycrystal is generated by Voronoi 
tessellations. The polycrystal is constituted of single crystal which are polygons (for 2D 
problems) and polyhedrons (for 3D ones). The shape functions of the polygons and 
polyhedrons have been recently provided in [11]. 
2. Derivation of bounds with FFT schemes 
2.1. The cell problem for linear elastic composites with prescribed macroscopic strain 
or stress 
 We consider a heterogeneous elastic material defined by a parallelepipedic unit 
cell and three (two for plane strain or plane stress problems) vectors of translation 
invariance. The unit cell is made up of M phases whose elastic tensor (resp. compliance) 
 1
is denoted by (resp.  () ) for = 1M. At local scale, the compatibility 
equations, linear elastic constitutive equations, equilibrium and periodic conditions at 
the boundary of the idealized unit cell can be summered as follows: 
 1 t
  ()()(),x  u x  u x  x V (1) 
 2
 (x ) ( x ) :  ( x ),  x V
 div( ( x )) 0,  x V
 u( x ) E . x periodic
  (x ). n antiperiodic
in which the stiffness tensor ()x (resp. the compliance) of the heterogeneous medium 
is given by: 
 ()(),()()x  I x  x  I x  
 (2) 
 1 if x V
 with I ( x ) 
 0 if x V V
74 
 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
I () x for = 1M are the characteristic functions describing volumes V which 
 I ( x ) 1 E 
comply with   . Prescribed macroscopic strain V or macroscopic 
  ...  convolution product and then to ensure the 
bound character of the solutions. Moreover, the method accounts for the real geometry 
of the cell when exact Fourier coefficients of the characteristic function are used while 
the product between the elastic tensor with the strain is made with the approximation: 
 ˆ 1 ˆ 
 n FFT I()() x n FFT  n (19) 
 α α
in which I (xn) are the values of I (x) computed at the nodes of a regular grid in the real 
space. The shape functions account for the real geometry of the unit cell when the exact 
expressions of these functions could be derived. The lower bound for the elastic tensor 
is computed with the stress based iterative scheme. This scheme has been formulated by 
using [4, 5]: 
78 
 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
 p
 i 1 i i 
 ˆ ˆ0 ˆ 
 n   n  n::    n  (20) 
 1 
 ˆ 0
which is initialized with ˆn 0 for any n 0 and ˆ0  . In Eq. (20), n are the 
Fourier coefficients of the Green tensor for the stress, defined by: 
 2 (3  2  )
  ˆ 0  0  0: ˆ 0 :  0 0 0 0  2    (21) 
 n n 1 n 0 3 n 
 0 2  0
 ˆ 0
for n 0 and n 0 for n = 0. 
 At each step of the stress based iterative scheme, we need to compute ˆ n 
obtained as the convolution product between the shape functions and the stress. ˆ n is 
computed from Eq. (18) in which the strain ε is replaced by the stress σ at both sides of 
the equality. The convergence test used for the strain based iterative scheme is based on 
the equilibrium for stress. The dual scheme uses a convergence condition based on the 
compatibility of the strain: 
 p p 
 0ˆ 0 ˆ 
 strain-scheme: n :   :( n )  ,stress-scheme:  n :   :(  n )  (22) 
 1 1 
Typically, the precision in the interval [10−4, 10−3] can guarantee the convergence 
condition of this scheme (see [8]). Where the precision  =10−4 is considered in the 
applications. It is worth noted that the iterative schemes (15) and (20) are formally 
equivalent to those introduced in [1, 13] and [4, 5]. 
3. Application to 2D-polycrystals 
3.1. Local elastic law 
 We consider a 2D-polycrystal made up of M single cubic-crystals. The elastic 
tensor of the crystal α is denoted by with the components Cijkl (i, j, k, l = 1, 2). For 
convenience, it is more suitable to read the local elasticity rule with a matrice 
representation. For instance, in the 2D case, the elastic law written in the basis Bα 
oriented along the axis of the crystal is: 
 1 CCC 11 12 16  1 
  CCC  (23) 
 2 12 22 26 2 
  CCC  
 6 BB 16 26 66 6 
 B 
where the following notation has been used for the components of the strain and 
the stress: 
 79
Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
 1  11  1  11
  ,   (24) 
 2 22 2 22 
   
 6 212 6 2  12 
and the components Cij are related to those of Cijkl by: 
 CCC CCC1111 11222 1112
 11 12 16 
 CCCCCC12 22 26 1122 22222 2212 (25) 
 CCC16 26 66 2CCC 2 2
 B 1112 2212 1212 
 B 
The elasticity law in the crystal is assumed to be cubic. As a consequence the material 
has three independent elastic coefficients  , 1 , 2 and: 
 CCC11 12 16  2  1  0 
 CCC   2  0 (26) 
 12 22 26 1 
 CCC16 26 66 0 0 2 2 
 B 
In the FFT method, the strain and the stress are computed in a global frame B . The 
components of the elastic tensor must be computed in this global frame. Let author 
denote by ε′i and σ′i the components of the strain and stress written in the global frame. 
The orientation of the crystal in the global frame is given by the angle θ. 
 Fig. 1. Orientation θ of the single crystal in the global frame 
The base change relations giving the components of the strain ε′i as function of εi are: 
 2 2
 '1 c  1 s  2 2 cs  6 (27) 
 2 2
 '2 s  1 c  2 2 cs  6 (28) 
 2 2
 '6 2cs (  2  1 ) ( c s )  6 (29) 
in which c = cos(θ) and s = sin(θ). The relations giving the components σ′i as function of σi: 
80 
 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
 2 2
 1 c  1 s  2 2 cs  6 (30) 
 2 2
 2 s  1 c  2 2 cs  6 (31) 
 2 2
 6 2cs (  2  1 ) ( c s )  6 (32) 
Introducing Eq. (27) to Eq. (32) in relation (33) with (26) leads to: 
 CCC11 12 16 1
 1 
  CCC  (33) 
 2 12 22 26 2 
  6 
 B CCC16 26 66 6
 BB 
in which the components Cij ' are given by: 
 2 2
 C11 C 22  2  1 4(  2  1 ) c s
 C  4(   ) c2 s 2
 12 1 2 (34) 
 2 2
 C16 C 26 2 2( 1  2 ) cs ( s c )
 2 2
 C66 2 2 8(  1  2 ) c s
It is readily observed that the components of Cij ' are the same those Cij as soon as 
1  2 . This corresponds to the particular case of an isotropic elastic medium. 
3.2. The shape function of a polygon 
 The representative cell of the polycrystal is generated by Voronoi tessellations. 
Each single crystal is then represented by a polygon. The number of edges of the 
polygon is arbitrary. In a given microstructure, the polygons must contain 3, 4, 5,... 
edges. Consider a polygon and let us denote the positions of the corners by r1 , r2 , 
r2 ,..., ri , the corners being numbered in counter-clockwise direction. The shape function 
I and the area S of the α-polygon are given by the expressions in [16]: 
 J ()r r r r 
 ˆ i e3  j j 1 j j 1
 I( ) 2  ( rj r j 1 )sin c  exp i  (35) 
 S  j 1 2 2 
 J
 1
 S e3 rj  r j 1 (36) 
 2 j 1
with the convention r0 rj ,  is the norm of  , e3 is the normal unit vector to the 
working plane ( e1 , e2 ). In the above equation SLL 1 2 is the area of the squared unit 
cell. It is noted that this expression is preferred over another equivalent expression 
 81
Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
existing in literature for the regularity of the sinc function. In the latter analytical 
expression, the denominator can vanish at some values of the wave vectors, requiring 
attention when implementing these formulas. Indeed, sinc(x) tends to zero when x also 
tends to zero, but numerically, when x = 0, sinc(x) leads to singularity. The limit must 
 rj r j 1 
be correctly computed when the term  is null. 
 2
3.3. Illustration 
 Fig. 2. Unit cell of the Voronoi periodic structure 2D 
 A representative cell of the polysristal is obtained with Voronoi tesselation and is 
represented in Fig. 2. The orientation of each crystal, defined by the angle θ, is 
randomly chosen in the interval [0, π]. The elastic moduli of the cubic crystal are 
1 1, 2 2 and  1. The calculations are performed on 40 reconstructed unit cells. 
The average value of the effective elastic moduli are λhom and µhom. 
 Fig. 3. Variation of the effective elastic shear modulus µhom as function of the resolution 
82 
 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
 The variations of the homogenized elastic shear modulus with the number of wave 
vectors are provided in Fig. 3. Three solutions are provided in this figure, the strain and 
the stress based FFT bounds computed with the shape functions, the solution obtained 
with the original FFT iterative scheme of Moulinec and Suquet [1] without using the 
shape function. It is observed that the bounds have a uniform convergence and the 
solution of obtained with the original scheme of Moulinec and Suquet is comprised 
between the two bounds. 
4. Extension to 3D-polycrystals 
 In this section, we propose to extend the method based on the shape function to 
the case of 3D polycrystals. 
4.1. The shape function of a polyhedron 
 Each crystal of the 3D-polycrystal is represented by a polyhedron. It is defined by 
its K faces denoted Γk for k = 1...K. Each face Γk is a Jk-polygon given by the simple 
polygonal vertex chain rk ,1 ;...; rk, j and by the normal unit vector nˆk pointing towards 
the outside of the polyhedron. The shape function of the α-polyhedron is  0 
 K ˆ
 ˆ i .nk
 I ()()  2 k  (37) 
 V k 1 
where V denotes the volume of the unit cell and 
 J
 nˆk  ()rk, j r k , j 1 r k , j r k , j 1 
 k(  ) i ( r k, j r k , j 1 )sin c  exp i  (38) 
 .qk .  j 1 2 2 
where the convention rk,0 r k , j must be used. The two order tensor qk is the projector 
onto the plane normal to the unit vector nˆk : 
 qk I nˆ k  n ˆ k (39) 
Note that k ()  is the 2D-shape function of the polygon k without the area S of the 2D 
unit cell. Indeed, when the polygon if embedded in a squared unit cell, the shape 
function is k ()/  S where S denotes the area of the unit cell. The volume of a 
polyhedron can be conveniently computed from: 
 i KJ
 ˆ ˆ
 V  nk( r k, j 1  r k , j )( n k r k , j ) (40) 
 6 k 1 j 1
4.2. Numerical Analysis 
 The homogenized elastic coefficients of the polycrystal are now computed with the 
method based on the shape functions. A unit cell of the polycrystal is shown in Fig. 4. 
 83
Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
The cell contains 60 single cubic crystals. The orientation of each crystal is given by the 
three Euler angles θ1, θ2 and θ3 randomly chosen in the interval [0, π]. 
 Fig. 4. Unit cell of the 3D-polycrystal (60 single crystals) 
 The effective shear modulus and effective compressibility with the number of 
wave vectors are presented in Fig. 5 and Tab. 1. The result shows that the Moulinec and 
Suquet solution is again between the two bounds. 
 Tab. 1. Average values of the effective shear modulus and effective compressibility computed 
 for the 3D-polycrystal as function of the resolution. Comparison between the lower bound (LB) and the 
 upper bound (UB) and the solutions obtained with the orifinal scheme of Moulinec and Suquet (M&S) 
 µhom khom 
 Resolution 
 UB LB M&S UB LB M&S 
 4x4x4 1.5202 1.4705 1.4999 1.7187 1.7149 1.7178 
 8x8x8 1.5092 1.4877 1.4953 1.7202 1.7150 1.7195 
 16x16x16 1.5041 1.4904 1.4946 1.7207 1.7151 1.7203 
 32x32x32 1.5016 1.4913 1.4941 1.7211 1.7153 1.7207 
 64x64x64 1.5001 1.4916 1.4938 1.7212 1.7156 1.7209 
 96x96x96 1.4992 1.4924 1.4937 1.7212 1.7156 1.7210 
 128x128x128 1.4983 1.4927 1.4935 1.7213 1.7153 1.7211 
 256x256x256 1.4975 1.4934 1.4934 1.7213 1.7154 1.7211 
84 
 Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
 1.6 
 FFT upper bound
 FFT lower bound
 1.55 Moulinec & Suquet 1994
 1.5
 1.45
 hom
 
 1.4
 1.35
 1.3 
 0 50 100 150 200 250
 Resolution (2N) 
 Fig. 5. Variations of the effective shear modulus µhom as function of the resolution 
5. Conclusion 
 In this paper we provide rigorous bounds for 2D and 3D elastic polycrystals. The 
effective elastic coefficients are computed from reconstructed unit cell using standard 
methods based on Vornoi tesselations. In each single crystal, the elastic law is assumed 
to be cubic. The effective elastic coefficients are computed by using the FFT methods 
combined with the use of the shape functions. The method has been introduced by [5] 
for composites with ellipsoidal inclusions. The present approach has been extended to 
the case of polycrystal by taking advantages of the exact expressions of the shape 
function of polygon and polyhedron recently provided in [11]. 
References 
1. H Moulinec (1994). A fast numerical method for computing the linear and nonlinear 
 mechanical properties of composites. CR Acad. Sci. Paris, 318, pp. 1417-1423. 
2. WF Brown (1955). Solid mixture permittivities. J. Chem. Phys., 23(8), pp. 1514-1517. 
3. E Kroner (1972). Statistical continuum mechanics, 92, Springer. 
4. K Bhattacharya and PM Suquet (2005). A model problem concerning recoverable strains of 
 shape-memory polycrystals. Proc. R. Soc. A, 461(2061), pp. 2797-2816. 
5. G Bonnet (2007). Effective properties of elastic periodic composite media with fibers. 
 J. Mech. Phys. Solids, 55(5), pp. 881-899. 
6. DJ Eyre and GW Milton (1999). A fast numerical scheme for computing the response of 
 composites using grid refinement. Eur. Phys. J. Appl. Phys., 6(01), pp. 41-47. 
7. JC Michel, H Moulinec, and P Suquet (2001). A computational scheme for linear and 
 nonlinear composites with arbitrary phase contrast. International Journal for Numerical 
 Methods in Engineering, 52(1-2), pp. 139-160. 
 85
Journal of Science and Technique - N.203 (11-2019) - Le Quy Don Technical University 
8. V Monchiet and G Bonnet (2012). A polarization-based FFT iterative scheme for 
 computing the effective properties of elastic composites with arbitrary contrast. Int. J. 
 Numer. Meth. Eng., 89, pp. 1419-1436. 
9. S Nemat-Nasser and M Hori (1999). Micromechanics: Overall properties of heterogeneous 
 materials. Elsevier Amsterdam. 
10. V Monchiet (2015). Combining FFT methods and standard variational principles to 
 compute bounds and estimates for the properties of elastic composites. Computer Methods 
 in Applied Mechanics and Engineering, 283, pp. 454-473. 
11. J Wuttke (2017). Form factor (Fourier shape transform) of polygon and polyhedron. arXiv 
 preprint arXiv:1703.00255. 
12. GW Milton (2002). The theory of composites, 6. Cambridge University Press. 
13. H Moulinec and P Suquet (1998). A numerical method for computing the overall response 
 of nonlinear composites with complex microstructure. Computer methods in applied 
 mechanics and engineering, 157(1-2), pp. 69-94. 
14. L Walpole (1981). Elastic behavior of composite materials: Theoretical foundations. Adv. 
 Appl. Mech., 21, pp. 169-242. 
15. PP Castaneda and P Suquet (1999). Nonlinear composites. In Advances in applied 
 mechanics, 34, Elsevier, pp. 171-302. 
16. HL Nguyen and QD To (2018). Conductivity of composites with multiple polygonal 
 aggregates, theoretical estimates and numerical solutions from polarization series. 
 International Journal of Engineering Science, 123, pp. 109-116. 
TÍNH TOÁN BIÊN GIỚI HẠN THUỘC TÍNH ĐÀN HỒI CỦA ĐA TINH THỂ 
 TRÊN CƠ SỞ PHƯƠNG PHÁP BIẾN ĐỔI NHANH FOURIER 
 Tóm tắt: Bài báo trình bày vùng giới hạn số của các thuộc tính đàn hồi của đa tinh thể 
(polycrystals). Các hệ số đàn hồi đồng nhất được tính toán từ cấu trúc kiểu Voronoi. Kết quả 
chính của bài báo là đưa ra giới hạn biên trên và biên dưới xác định cho trường hợp cấu trúc 
đa tinh thể được tạo thành từ các tinh thể đơn khối bằng cách sử dụng phương pháp biến đổi 
nhanh Fourier (FFT) dựa trên cơ sở hàm dạng. Phương pháp của tác giả đảm bảo các kết quả 
tính toán chính xác hơn so với phương pháp của Moulinec và Suquet trong đó tồn tại một số 
xấp xỉ không kiểm soát được. Phương pháp đề xuất có thể mở rộng để tính toán cho các vật liệu 
đối xứng khác như tinh thể lục giác hoặc tứ giác. 
 Từ khóa: Hệ số đàn hồi; giới hạn biên số; hàm dạng; kết cấu đa tinh thể; Voronoi; biến đổi 
nhanh Fourier. 
 Received: 12/4/2019; Revised: 12/11/2019; Accepted for publication: 22/11/2019 
  
86