Compression effects on structural relaxation process of amorphous indomethacin

 Communications in Physics, Vol.31, No. 1 (2021), pp. 67-76
 DOI:10.15625/0868-3166/15377
 COMPRESSION EFFECTS ON STRUCTURAL RELAXATION PROCESS OF
 AMORPHOUS INDOMETHACIN
 TRAN DINH CUONG1,† AND ANH D. PHAN1,2,‡
1Phenikaa Institute for Advanced Study (PIAS), Phenikaa University, Hanoi 12116, Vietnam
2Faculty of Computer Science, Materials Science and Engineering, Artificial Intelligence
 Laboratory, Phenikaa University, Hanoi 12116, Viet Nam
 E-mail: †cuong.trandinh@phenikaa-uni.edu.vn; ‡anh.phanduc@phenikaa-uni.edu.vn
 Received August 15, 2020
 Accepted for publication 16 October 2020
 Published 8 January 2021
 Abstract. Indomethacin is a common nonsteroidal anti-inflammatory drug, but its glass transition
 behaviors remain ambiguous. Here we present a simple theoretical approach to investigate the
 molecular mobility of amorphous indomethacin under compression. In our model, the relaxation
 of a particle is governed by its nearest-neighbor interactions and long-range cooperative effects
 of fluid surroundings. On that basis, the temperature and pressure dependence of the structural
 relaxation time is deduced from the thermal expansion process. Additionally, we also consider
 correlations between the activated dynamics and the shear response in the deeply supercooled
 state. Our numerical calculations agree quantitatively well with previous experimental works.
 Keywords: compression effects, structural relaxation, amorphous drug, indomethacin.
 Classification numbers: 65.60.+a.
 I. INTRODUCTION
 Indomethacin (IMC) has been intensively studied for decades because of its peculiar prop-
 erties [1–3]. This nonselective cyclooxygenase inhibitor is useful for treating joint diseases [4],
 headaches [5], and patent ductus arteriosus [6]. In addition, one can apply IMC to design smart
 probes for identifying cancer cells [7–9]. However, the commercial form of IMC exhibits poor
 aqueous solubility and low bioavailability [10]. Hence, a large dosage of IMC must be delivered
 to patients to achieve the therapeutic effect. The event may increase the risk of gastrointestinal tox-
 icity [11]. One of the promising strategies to overcome these drawbacks is to prepare IMC in the
 amorphous form [12–14]. Unfortunately, the disordered atomic structure is thermodynamically
 ©2021 Vietnam Academy of Science and Technology
68 T. D. CUONG AND A. D. PHAN
unstable. The crystallization readily occurs during manufacturing, storage, or dissolution [12–14].
Consequently, precise knowledge of relaxation processes in IMC is essential for reinforcing its
physical stability.
 In experiments, the structural relaxation time, τα , is typically measured by the broadband
dielectric spectroscopy (BDS) technique [14–16]. The global atomic rearrangement causes a
prominent, broad, and asymmetry α-peak on the dielectric loss spectra. From these, one can
capture a dramatic growth of τα upon isobaric cooling or isothermal squeezing [14–16]. When
 2
τα reaches 10 s, amorphous pharmaceutical systems undergo the glass transition and fall out of
equilibrium. In the glassy state, since cooperative motions become frozen, τα is often indirectly
estimated by a master plot construction [14]. Notably, recent BDS studies [17] have revealed that
compression effects can suppress the strong crystallization tendency of IMC. Nevertheless, the
underlying mechanism of these phenomena has remained ambiguous.
 Apart from BDS measurements, one can use the Elastically Collective Nonlinear Langevin
Equation (ECNLE) theory to gain insights into the molecular mobility of amorphous drugs [18–
20]. The ECNLE theory considers the α-relaxation as a dynamic coupling between local and
collective activated events [18–20]. On that basis, the thermal response of τα is determined by
analyzing the bulk expansion process [18–20]. At ambient pressure, ECNLE calculations can
 −12 2
provide τα from 10 to 10 s, which is far beyond the simulation timescale [18–20]. Recently,
Phan et al. [21, 22] have modified the free energy profile to access the high-pressure regime. The
obtained results for τα of Phan et al. [21,22] are in good agreement with BDS data. However, the
modified ECNLE model [21, 22] may lead to incorrect predictions of the dynamic fragility.
 In this paper, we extend the ECNLE analysis to solve the mentioned limitations. Numerical
calculations are carried out for IMC up to 226 MPa. Besides, correlations between the structural
relaxation time, the fragility index, and the instantaneous shear modulus are comprehensively
discussed. Our theoretical results are quantitatively compared with prior experiments.
II. THEORETICAL BACKGROUND
 In the ECNLE theory [18–22], an amorphous drug is described by an effective hard-sphere
fluid having the particle diameter, σ, the particle number density, ρ, and the packing fraction,
Φ = πρσ 3/6. Structural properties of the reference system are inferred from the Percus-Yevick
approximation  ... )
 5π σrL
 The activated hopping event of the tagged particle requires the rearrangement of its nearest
neighbors [29–31]. Therefore, one can observe a small increase in the cage’s volume. This local
dilation excites a harmonic displacement field, u(r), in the surrounding fluid. Utilizing Lifshitz’s
continuity equation [32] provides
 r 2
 u(r) = ∆r cage , r ≥ r , (10)
 e f f r cage
 2
where ∆re f f ≈ 3∆r /32rcage is the cage expansion amplitude [29–31].
 According to Einstein’s glass picture, fluid particles outside the cage vibrate with the same
  2 2

harmonic force constant, KL = ∂ Fdyn/∂r . Consequently, the strain energy, known as the
 r=rL
collective elastic barrier, is computed by [29–31]
 Z ∞ 3
 1 2 2 2 rcage 
 FE = KLu (r)ρg(r)4πr dr ≈ 12Φ∆re f f KL, (11)
 rcage 2 σ
where g(r) ≈ 1 for r ≥ rcage. From Eqs. (9) and (11), one can associate FE with G∞ at the deeply-
supercooled regime by
 2 3
 ∆re f f rcage
 F = 20π G . (12)
 E σ 2 ∞
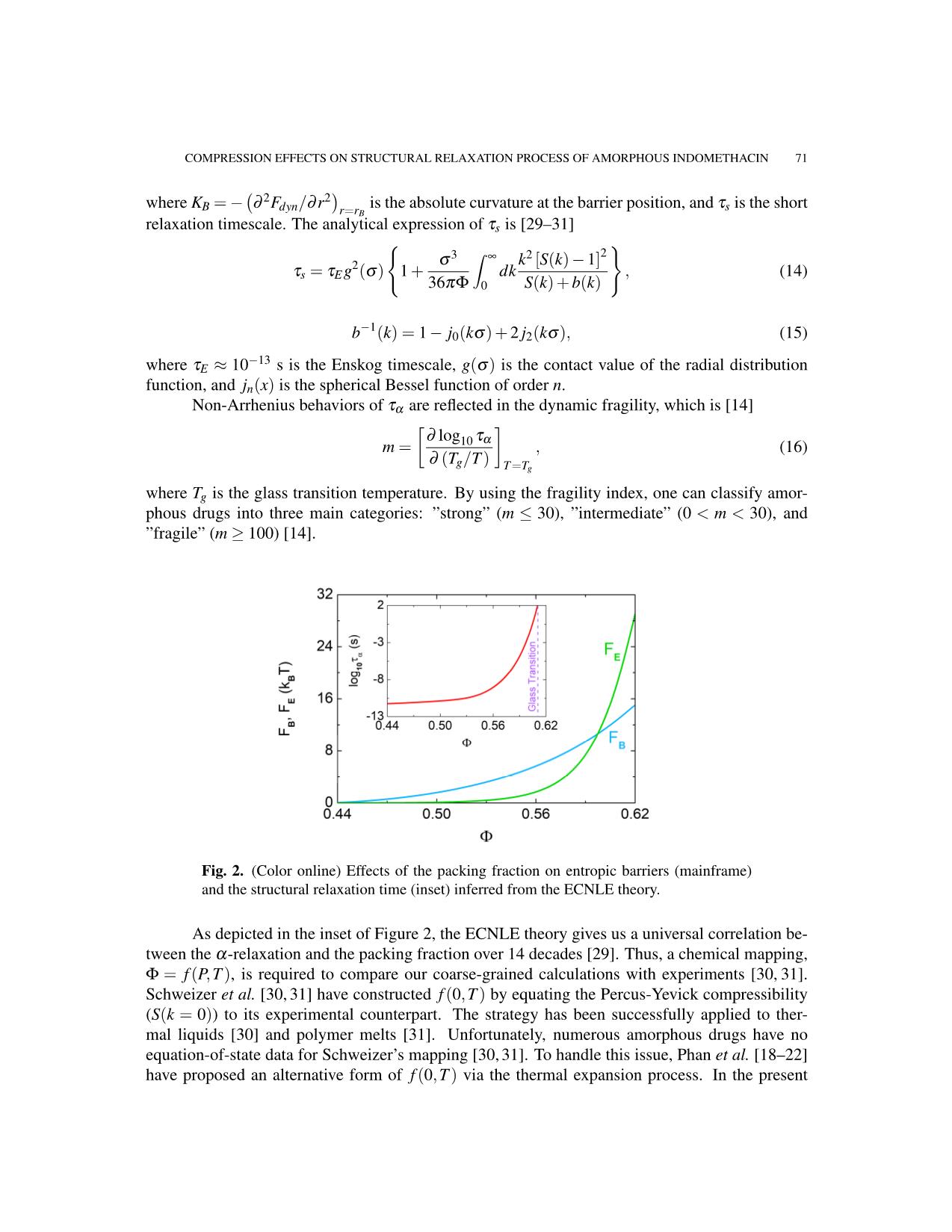
 Figure 2 shows how FB and FE depend on the packing fraction. Essentially, one can neglect
FE in a range of 0.43 0.57), FE grows much
faster than its local analog. Entropic barrier profiles cross each other at Φ ≈ 0.6. This result affirms
the dominance of collective dynamics in the α-relaxation near kinetic vitrification [29–31].
 Recall that τα is defined as the average time for the tagged particle to escape from its cage.
Adopting the modified Kramers’ theory yields [29–31]
  2π k T F + F 
 √ B B E
 τα = τs 1 + 2 exp , (13)
 KLKB σ kBT
 COMPRESSION EFFECTS ON STRUCTURAL RELAXATION PROCESS OF AMORPHOUS INDOMETHACIN 71
  2 2

where KB = − ∂ Fdyn/∂r is the absolute curvature at the barrier position, and τs is the short
 r=rB
relaxation timescale. The analytical expression of τs is [29–31]
 ( 3 Z ∞ 2 2 )
 2 σ k [S(k) − 1]
 τs = τE g (σ) 1 + dk , (14)
 36πΦ 0 S(k) + b(k)
 −1
 b (k) = 1 − j0(kσ) + 2 j2(kσ), (15)
 −13
where τE ≈ 10 s is the Enskog timescale, g(σ) is the contact value of the radial distribution
function, and jn(x) is the spherical Bessel function of order n.
 Non-Arrhenius behaviors of τα are reflected in the dynamic fragility, which is [14]
 ∂ log τ 
 m = 10 α , (16)
 ∂ (T /T)
 g T=Tg
where Tg is the glass transition temperature. By using the fragility index, one can classify amor-
phous drugs into three main categories: ”strong” (m ≤ 30), ”intermediate” (0 < m < 30), and
”fragile” (m ≥ 100) [14].
 Fig. 2. (Color online) Effects of the packing fraction on entropic barriers (mainframe)
 and the structural relaxation time (inset) inferred from the ECNLE theory.
 As depicted in the inset of Figure 2, the ECNLE theory gives us a universal correlation be-
tween the α-relaxation and the packing fraction over 14 decades [29]. Thus, a chemical mapping,
Φ = f (P,T), is required to compare our coarse-grained calculations with experiments [30, 31].
Schweizer et al. [30, 31] have constructed f (0,T) by equating the Percus-Yevick compressibility
(S(k = 0)) to its experimental counterpart. The strategy has been successfully applied to ther-
mal liquids [30] and polymer melts [31]. Unfortunately, numerous amorphous drugs have no
equation-of-state data for Schweizer’s mapping [30, 31]. To handle this issue, Phan et al. [18–22]
have proposed an alternative form of f (0,T) via the thermal expansion process. In the present
72 T. D. CUONG AND A. D. PHAN
work, we extend Phan’s mapping [18–22] to appropriately take into account compression effects.
The f (P,T) function is written by
 Φ = f (P,T) = Φ0 {1 − β(P)[T − T0(P)]}, (17)
where P is hydrostatic pressure, Φ0 is the initial packing fraction, β is the bulk thermal expansivity,
and T0 is the characteristic temperature. Remarkably, in most cases, the original Schweizer’s
mapping [30,31] can be well fitted by Eq. (17) with Φ0 = 0.5 [27]. We keep utilizing this common
value to consider the glassy dynamics of IMC.
 Material-specific details (e.g., molar mass and particle size) are encoded in T0 [18–22].
 2
Since Eq. (13) indicates τα = 10 s at Φ = Φg = 0.611, we can directly link T0 to Tg by
 Φg − Φ0
 T0 = Tg + . (18)
 βΦ0
For simplicity, Tg is taken from experiments. The obtained results are often described by
  1/k2
 k2
 Tg = k1 1 + P , (19)
 k3
where k1, k2, and k3 are Andersson’s parameters [33]. On that basis, the pressure dependence of β
is supposed to be [34–36]
  −1
 k2
 β = β0 1 + P , (20)
 k3
 −4 −1
where β0 = 12 × 10 K is employed to all organic materials [18–22].
III. RESULTS AND DISCUSSION
 2
 0 . 1 M P a
 0 9 0 M P a
 1 3 6 M P a
 ) 2 2 6 M P a
 s
 ( - 2
 a
 τ
 0
 1
 g
 o - 4
 l
 - 6
 - 8
 2 . 0 2 . 3 2 . 6 2 . 9 3 . 2
 1 0 0 0 / T ( K - 1 )
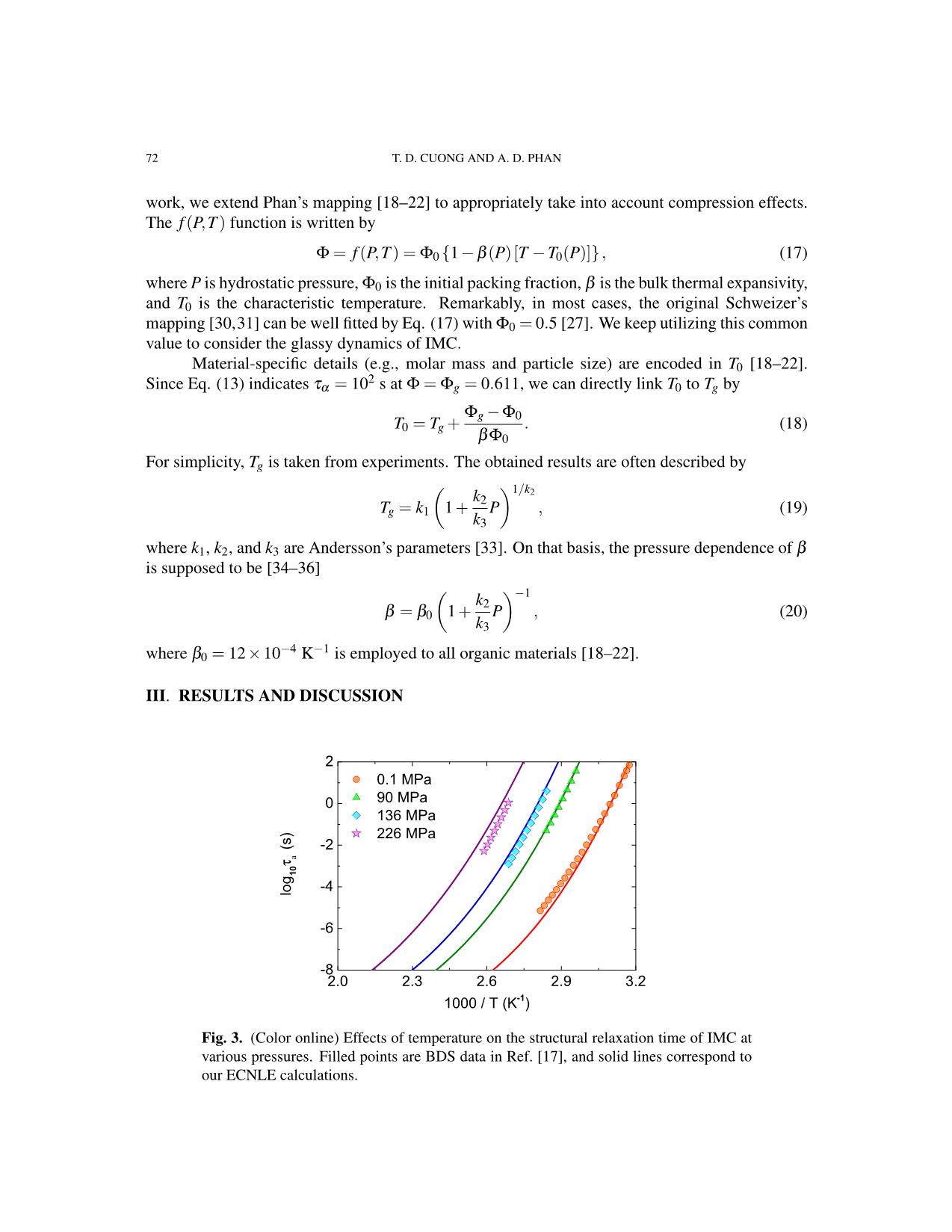
 Fig. 3. (Color online) Effects of temperature on the structural relaxation time of IMC at
 various pressures. Filled points are BDS data in Ref. [17], and solid lines correspond to
 our ECNLE calculations.
 COMPRESSION EFFECTS ON STRUCTURAL RELAXATION PROCESS OF AMORPHOUS INDOMETHACIN 73
 Figure 3 shows how log10 τα of IMC depends on 1000/T at different pressures. Ander-
sson’s parameters used for theoretical calculations are k1 = 315 K, k2 = 3.14, and k3 = 1238
 −1 −1
MPa [17]. Notably, a large value of k1k3 = 0.254 K.MPa suggests that IMC should be viewed
as a typical van der Waals liquid [37–43]. From these, we can capture a significant slowing down
of molecular dynamics upon isobaric cooling. The ECNLE analysis is in excellent agreement
with recent BDS measurements [17]. Consequently, our findings would be useful for the tableting
process of amorphous drugs.
 E C N L E E X P T
 1 0 0
 9 0 . 1
 8 2 . 8
 7 8 . 4 8 1 7 9 . 7
 7 3 . 7 7 5 . 2
 y
 t 7 5
 i
 l
 i 6 6 . 2
 g
 a
 r
 F
 c 5 0
 i
 m
 a
 n
 y
 D 2 5
 0
 0 . 1 M P a 9 0 M P a 1 3 6 M P a 2 2 6 M P a
 P r e s s u r e
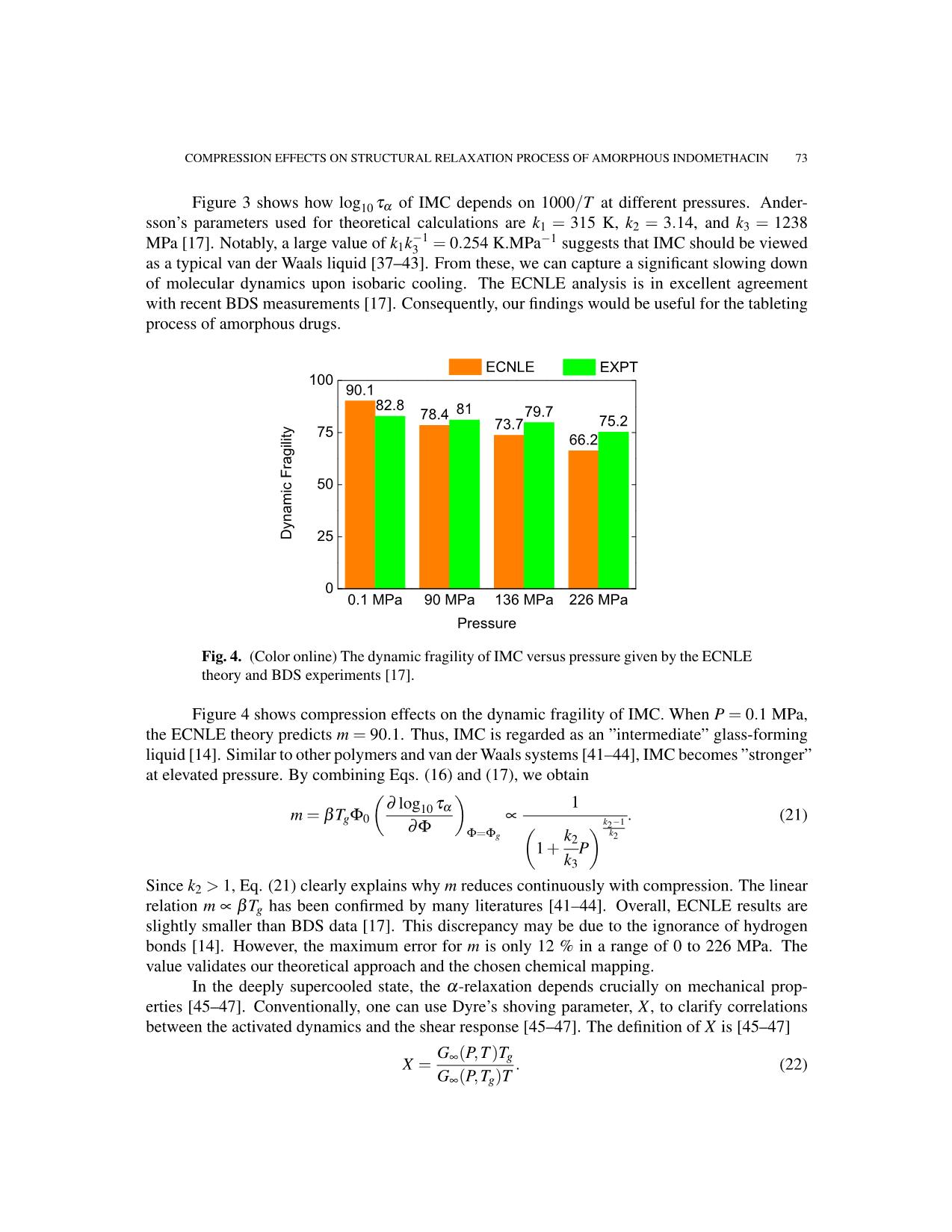
 Fig. 4. (Color online) The dynamic fragility of IMC versus pressure given by the ECNLE
 theory and BDS experiments [17].
 Figure 4 shows compression effects on the dynamic fragility of IMC. When P = 0.1 MPa,
the ECNLE theory predicts m = 90.1. Thus, IMC is regarded as an ”intermediate” glass-forming
liquid [14]. Similar to other polymers and van der Waals systems [41–44], IMC becomes ”stronger”
at elevated pressure. By combining Eqs. (16) and (17), we obtain
 ∂ log τ  1
 m = βT Φ 10 α ∝ . (21)
 g 0 k2−1
 ∂Φ Φ=Φ   k
 g k2 2
 1 + P
 k3
Since k2 > 1, Eq. (21) clearly explains why m reduces continuously with compression. The linear
relation m ∝ βTg has been confirmed by many literatures [41–44]. Overall, ECNLE results are
slightly smaller than BDS data [17]. This discrepancy may be due to the ignorance of hydrogen
bonds [14]. However, the maximum error for m is only 12 % in a range of 0 to 226 MPa. The
value validates our theoretical approach and the chosen chemical mapping.
 In the deeply supercooled state, the α-relaxation depends crucially on mechanical prop-
erties [45–47]. Conventionally, one can use Dyre’s shoving parameter, X, to clarify correlations
between the activated dynamics and the shear response [45–47]. The definition of X is [45–47]
 G (P,T)T
 X = ∞ g . (22)
 G∞(P,Tg)T
74 T. D. CUONG AND A. D. PHAN
Applying the ultra-local analysis (Eq. (9)) [28] and an exponential law rL = 30σ exp(−12.2Φ)
[24] provides
 Φexp(24.4Φ)
 X = . (23)
 Φg exp(24.4Φg)
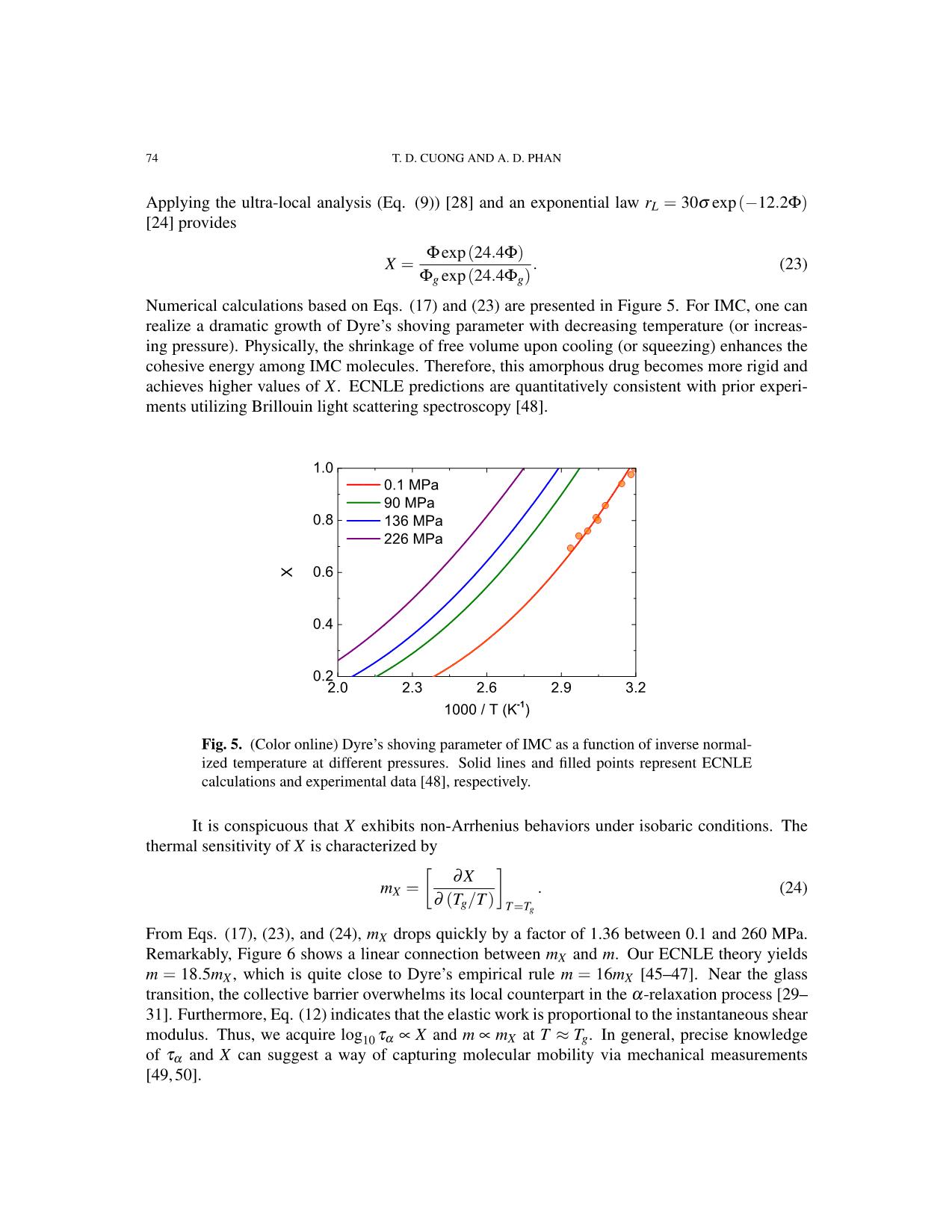
Numerical calculations based on Eqs. (17) and (23) are presented in Figure 5. For IMC, one can
realize a dramatic growth of Dyre’s shoving parameter with decreasing temperature (or increas-
ing pressure). Physically, the shrinkage of free volume upon cooling (or squeezing) enhances the
cohesive energy among IMC molecules. Therefore, this amorphous drug becomes more rigid and
achieves higher values of X. ECNLE predictions are quantitatively consistent with prior experi-
ments utilizing Brillouin light scattering spectroscopy [48].
 1 . 0
 0 . 1 M P a
 9 0 M P a
 0 . 8 1 3 6 M P a
 2 2 6 M P a
 X 0 . 6
 0 . 4
 0 . 2
 2 . 0 2 . 3 2 . 6 2 . 9 3 . 2
 1 0 0 0 / T ( K - 1 )
 Fig. 5. (Color online) Dyre’s shoving parameter of IMC as a function of inverse normal-
 ized temperature at different pressures. Solid lines and filled points represent ECNLE
 calculations and experimental data [48], respectively.
 It is conspicuous that X exhibits non-Arrhenius behaviors under isobaric conditions. The
thermal sensitivity of X is characterized by
  ∂X 
 m = . (24)
 X ∂ (T /T)
 g T=Tg
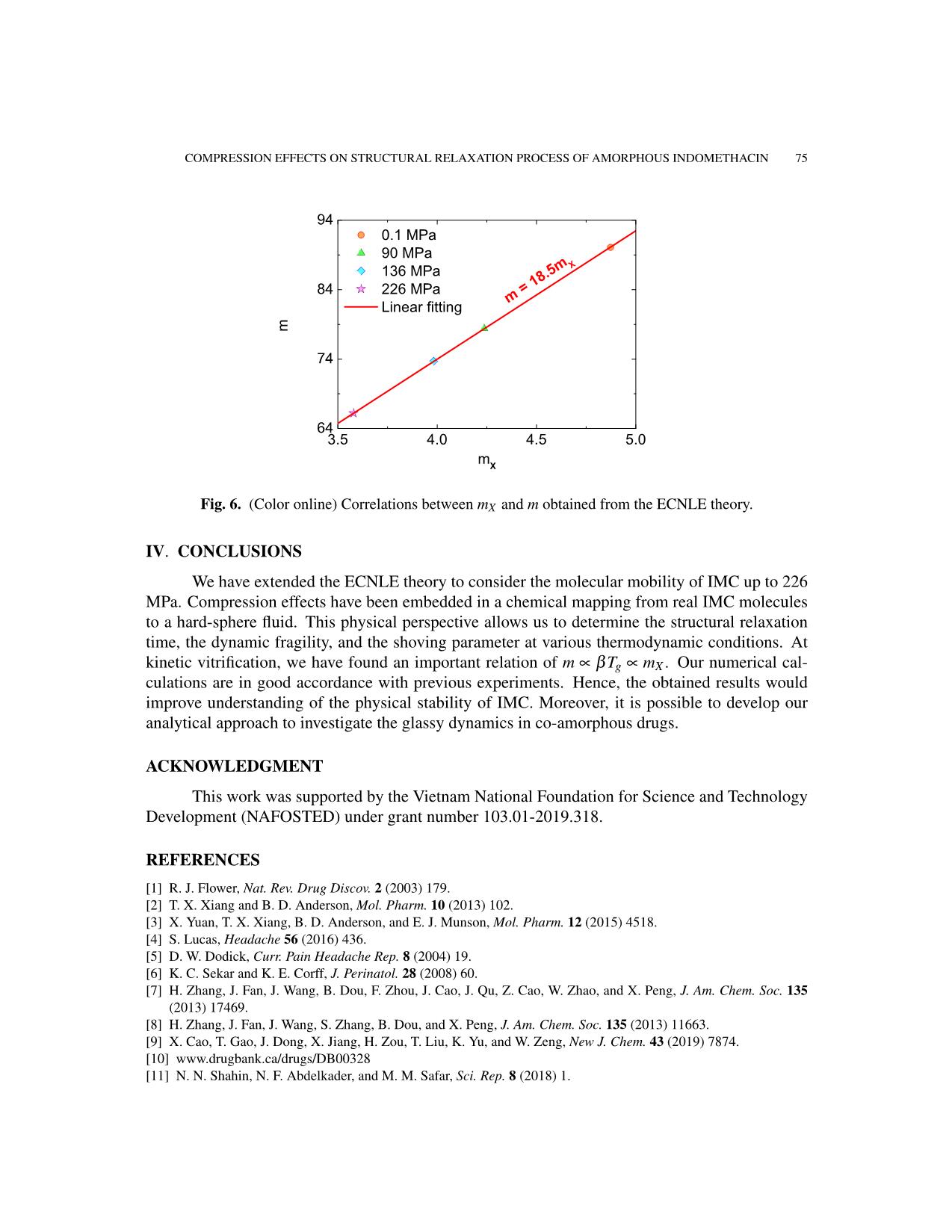
From Eqs. (17), (23), and (24), mX drops quickly by a factor of 1.36 between 0.1 and 260 MPa.
Remarkably, Figure 6 shows a linear connection between mX and m. Our ECNLE theory yields
m = 18.5mX , which is quite close to Dyre’s empirical rule m = 16mX [45–47]. Near the glass
transition, the collective barrier overwhelms its local counterpart in the α-relaxation process [29–
31]. Furthermore, Eq. (12) indicates that the elastic work is proportional to the instantaneous shear
modulus. Thus, we acquire log10 τα ∝ X and m ∝ mX at T ≈ Tg. In general, precise knowledge
of τα and X can suggest a way of capturing molecular mobility via mechanical measurements
[49, 50].
 COMPRESSION EFFECTS ON STRUCTURAL RELAXATION PROCESS OF AMORPHOUS INDOMETHACIN 75
 9 4
 0 . 1 M P a
 9 0 M P a
 5 m X
 1 3 6 M P a 8 .
 1
 8 4 2 2 6 M P a =
 m
 L i n e a r f i t t i n g
 m
 7 4
 6 4
 3 . 5 4 . 0 4 . 5 5 . 0
 m X
 Fig. 6. (Color online) Correlations between mX and m obtained from the ECNLE theory.
IV. CONCLUSIONS
 We have extended the ECNLE theory to consider the molecular mobility of IMC up to 226
MPa. Compression effects have been embedded in a chemical mapping from real IMC molecules
to a hard-sphere fluid. This physical perspective allows us to determine the structural relaxation
time, the dynamic fragility, and the shoving parameter at various thermodynamic conditions. At
kinetic vitrification, we have found an important relation of m ∝ βTg ∝ mX . Our numerical cal-
culations are in good accordance with previous experiments. Hence, the obtained results would
improve understanding of the physical stability of IMC. Moreover, it is possible to develop our
analytical approach to investigate the glassy dynamics in co-amorphous drugs.
ACKNOWLEDGMENT
 This work was supported by the Vietnam National Foundation for Science and Technology
Development (NAFOSTED) under grant number 103.01-2019.318.
REFERENCES
[1] R. J. Flower, Nat. Rev. Drug Discov. 2 (2003) 179.
[2] T. X. Xiang and B. D. Anderson, Mol. Pharm. 10 (2013) 102.
[3] X. Yuan, T. X. Xiang, B. D. Anderson, and E. J. Munson, Mol. Pharm. 12 (2015) 4518.
[4] S. Lucas, Headache 56 (2016) 436.
[5] D. W. Dodick, Curr. Pain Headache Rep. 8 (2004) 19.
[6] K. C. Sekar and K. E. Corff, J. Perinatol. 28 (2008) 60.
[7] H. Zhang, J. Fan, J. Wang, B. Dou, F. Zhou, J. Cao, J. Qu, Z. Cao, W. Zhao, and X. Peng, J. Am. Chem. Soc. 135
 (2013) 17469.
[8] H. Zhang, J. Fan, J. Wang, S. Zhang, B. Dou, and X. Peng, J. Am. Chem. Soc. 135 (2013) 11663.
[9] X. Cao, T. Gao, J. Dong, X. Jiang, H. Zou, T. Liu, K. Yu, and W. Zeng, New J. Chem. 43 (2019) 7874.
[10] www.drugbank.ca/drugs/DB00328
[11] N. N. Shahin, N. F. Abdelkader, and M. M. Safar, Sci. Rep. 8 (2018) 1.
76 T. D. CUONG AND A. D. PHAN
[12] M. Rams-Baron, R. Jachowicz, E. Boldyreva, D. Zhou, W. Jamroz, and M. Paluch, Amorphous Drugs, Springer,
 Heidelberg (2018).
[13] B. C. Hancock and M. Parks, Pharm. Res. 17 (2000) 397.
[14] K. Grzybowska, S. Capaccioli, and M. Paluch, Adv. Drug Deliv. Rev. 100 (2016) 158.
[15] E. Kaminska, K. Adrjanowicz, D. Zakowiecki, B. Milanowski, M. Tarnacka, L. Hawelek, M. Dulski, J. Pilch, W.
 Smolka, I. Kaczmarczyk-Sedlak, and K. Kaminski, Pharm. Res. 31 (2014) 2887.
[16] S. Mohapatra, S. Samanta, K. Kothari, P. Mistry, and R. Suryanarayanan, Cryst. Growth Des. 17 (2017) 3142.
[17] Z. Wojnarowska, K. Adrjanowicz, P. Wlodarczyk, E. Kaminska, K. Kaminski, K. Grzybowska, R. Wrzalik, M.
 Paluch, and K. L. Ngai, J. Phys. Chem. B 113 (2009) 12536.
[18] A. D. Phan, J. Knapik-Kowalczuk, M. Paluch, T. X. Hoang, and K. Wakabayashi, Mol. Pharm. 16 (2019) 2992.
[19] A. D. Phan, K. Wakabayashi, M. Paluch, and V. D. Lam, RSC Adv. 9 (2019) 40214.
[20] A. D. Phan, T. T. T. Thuy, N. T. K. An, J. Knapik-Kowalczuk, M. Paluch, and K. Wakabayashi, AIP Adv. 10 (2020)
 025128.
[21] A. D. Phan, A. Jedrzejowska, M. Paluch, and K. Wakabayashi, ACS Omega 5 (2020) 11035.
[22] A. D. Phan and K. Wakabayashi, Pharmaceutics 12 (2020) 177.
[23] J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Academic Press, London (2006).
[24] K. S. Schweizer and E. J. Saltzman, J. Chem. Phys. 119 (2003) 1181.
[25] K. S. Schweizer, J. Chem. Phys. 123 (2005) 244501.
[26] G. Ngele and J. Bergenholtz, J. Chem. Phys. 108 (1998) 9893.
[27] A. D. Phan and K. S. Schweizer, J. Phys. Chem. B 122 (2018) 8451.
[28] K. S. Schweizer, and G. Yatsenko, J. Chem. Phys. 127 (2007) 164505.
[29] S. Mirigian and K. S. Schweizer, J. Chem. Phys. 140 (2014) 194506.
[30] S. Mirigian and K. S. Schweizer, J. Chem. Phys. 140 (2014) 194507.
[31] S. Mirigian and K. S. Schweizer, Macromolecules 48 (2015) 1901.
[32] L. D. Landau and E. M. Lifshitz, Theory of Elasticity, Permagon Press, London (1975).
[33] S. P. Andersson and O. Andersson, Macromolecules 31 (1998) 2999.
[34] N. Dass and M. Kumari, Phys. Status Solidi (b) 124 (1984) 531.
[35] I. Avramov, A. Grzybowski, and M. Paluch, J. Non-Cryst. Solids 355 (2009) 733.
[36] M. Paluch, C. M. Roland, J. Gapinski, and A. Patkowski, J. Chem. Phys. 118 (2003) 3177.
[37] Z. Wojnarowska, K. Adrjanowicz, K. Kaminski, L. Hawelek, and M. Paluch, J. Phys. Chem. B 114 (2010) 14815.
[38] K. Adrjanowicz, K. Kaminski, Z. Wojnarowska, M. Dulski, L. Hawelek, S. Pawlus, M. Paluch, and W. Sawicki,
 J. Phys. Chem. B 114 (2010) 6579.
[39] K. Adrjanowicz, K. Kaminski, M. Paluch, and K. Niss, Cryst. Growth Des. 15 (2015) 3257.
[40] A. Patkowski, J. Gapinski, and G. Meier, Colloid Polym. Sci. 282 (2004) 874.
[41] C. M. Roland, S. Hensel-Bielowka, M. Paluch, and R. Casalini, Rep. Prog. Phys. 68 (2005) 1405.
[42] R. Casalini and C. M. Roland, Phys. Rev. B 71 (2005) 014210.
[43] M. Paluch, E. Masiewicz, A. Grzybowski, S. Pawlus, J. Pionteck, and Z. Wojnarowska, J. Chem. Phys. 141 (2014)
 134507.
[44] E. Masiewicz, A. Grzybowski, A. P. Sokolov, and M. Paluch, J. Phys. Chem. Lett. 3 (2012) 2643.
[45] T. D. Cuong, A. D. Phan, K. Wakabayashi, and P. T. Huy, J. Non-Cryst. Solids 538 (2020) 120024.
[46] J. C. Dyre, J. Non-Cryst. Solids 235 (1998) 142.
[47] C. Klieber, T. Hecksher, T. Pezeril, D. H. Torchinsky, J. C. Dyre, and K. A. Nelson, J. Chem. Phys. 138 (2013)
 12A544.
[48] K. L. Kearns, T. Still, G. Fytas, and M. D. Ediger, Adv. Mater. 22 (2010) 39.
[49] T. Hecksher and J. C. Dyre, J. Non-Cryst. Solids 407 (2015) 14.
[50] T. Hecksher, D. H. Torchinsky, C. Klieber, J. A. Johnson, J. C. Dyre, and K. A. Nelson, Proc. Natl. Acad. Sci.
 U.S.A. 114 (2017) 8710.