Chụp ảnh cắt lớp phân tử N₂ định phương không hoàn toàn từ phổ sóng điều hòa bậc cao

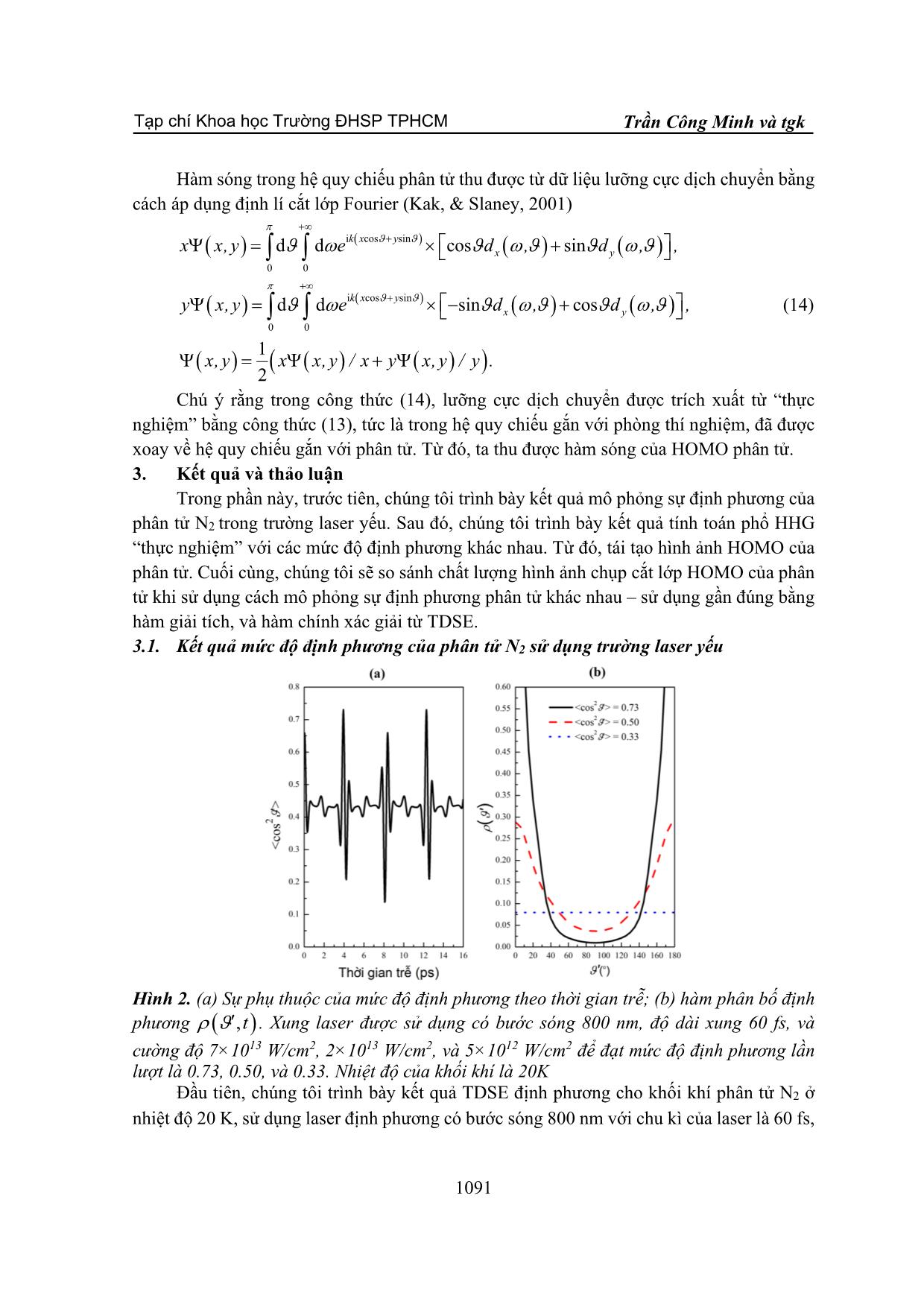
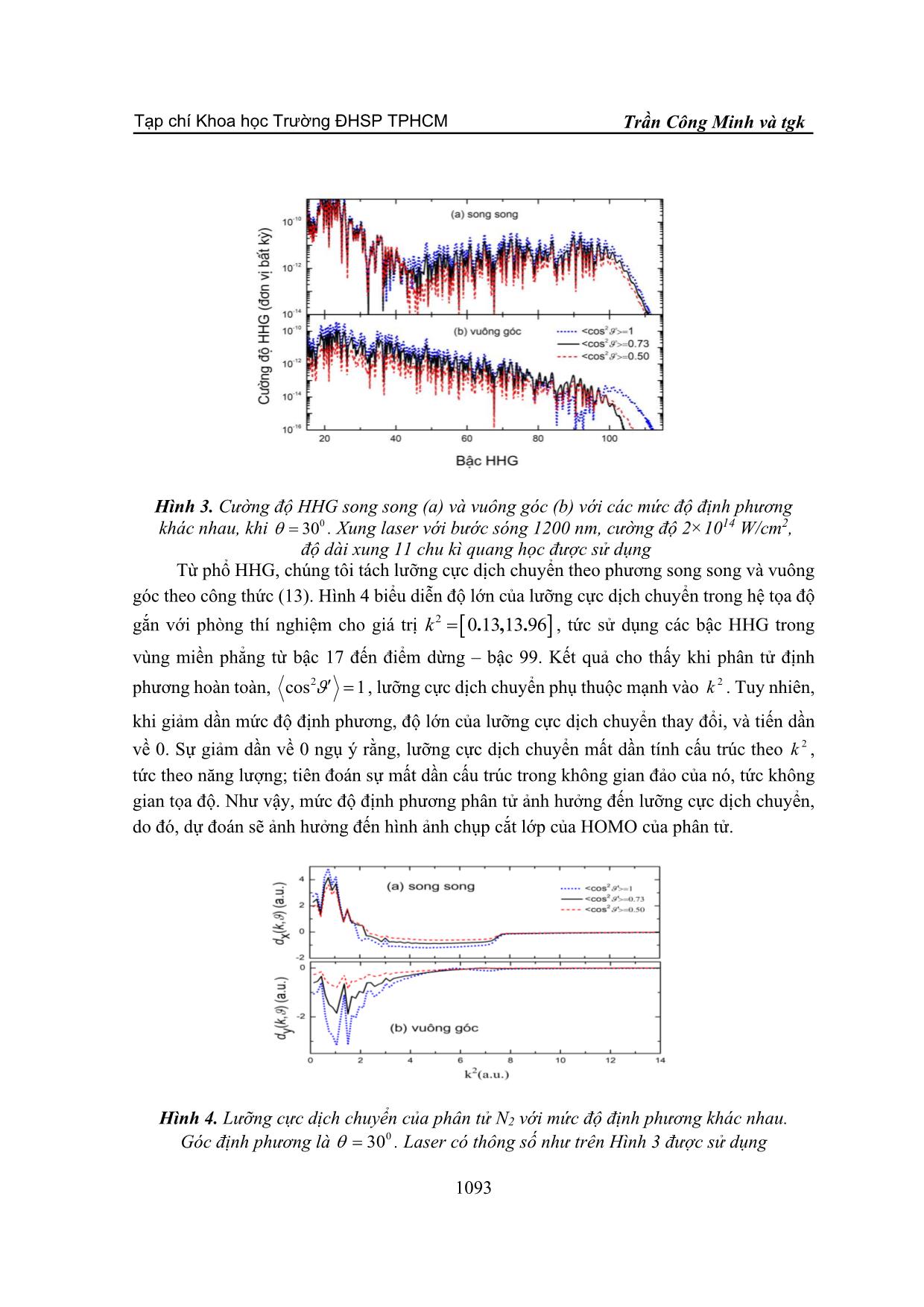
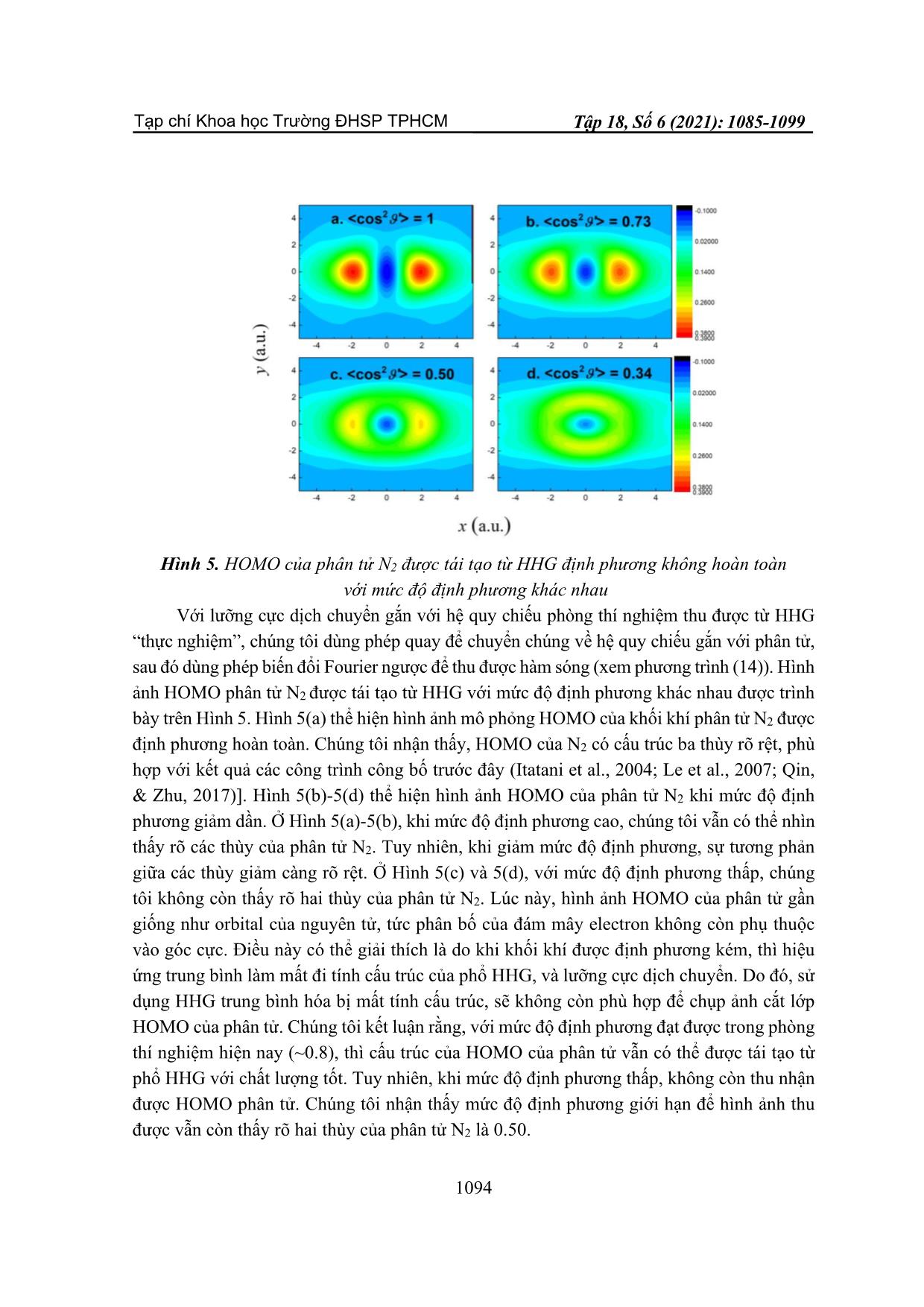
 TẠP CHÍ KHOA HỌC HO CHI MINH CITY UNIVERSITY OF EDUCATION 
 TRƯỜNG ĐẠI HỌC SƯ PHẠM TP HỒ CHÍ MINH JOURNAL OF SCIENCE 
 Tập 18, Số 6 (2021): 1085-1099 Vol. 18, No. 6 (2021): 1085-1099 
 ISSN: 
 2734-9918 Website:  
 Bài báo nghiên cứu* 
 CHỤP ẢNH CẮT LỚP PHÂN TỬ N2 ĐỊNH PHƯƠNG 
 KHÔNG HOÀN TOÀN TỪ PHỔ SÓNG ĐIỀU HÒA BẬC CAO 
 Trần Công Minh1, Trương Quân Hào1, Trần Phúc Khang1, 
 Lê Thị Cẩm Tú2, Phan Thị Ngọc Loan1* 
 1Trường Đại học Sư phạm Thành phố Hồ Chí Minh, Việt Nam 
 2Trường Đại học Tôn Đức Thắng, Việt Nam 
 *Tác giả liên hệ: Phan Thị Ngọc Loan – Email: loanptn@hcmue.edu.vn 
 Ngày nhận bài: 18-01-2021; ngày nhận bài sửa: 22-4-2021; ngày duyệt đăng: 08-6-2021 
TÓM TẮT 
 Chúng tôi tái tạo hình ảnh chụp cắt lớp đám mây electron lớp ngoài cùng (HOMO) từ phổ 
phát xạ sóng điều hòa bậc cao (HHG) của phân tử N2 khi xét đến hiệu ứng định phương không hoàn 
toàn. Chúng tôi đã sử dụng hai cách khác nhau để mô tả hàm phân bố định phương – (i) giải chính 
xác bằng số phương trình Schrӧdinger phụ thuộc vào thời gian, và (ii) gần đúng bằng hàm giải tích. 
Kết quả cho thấy rằng, mức độ định phương giảm dần, độ chính xác của HOMO của phân tử giảm 
dần. Khi mức độ định phương nhỏ hơn 0.5, thì không còn tái tạo được chính xác HOMO của phân 
tử. Ngoài ra, sử dụng hai cách mô tả hàm phân bố định phương đều cho kết quả tương tự nhau. 
 Từ khóa: sóng điều hòa bậc cao; phân tử N2; định phương không hoàn toàn; chụp ảnh cắt lớp 
1. Giới thiệu 
 Kể từ khi ra đời vào năm 1960 (Maiman, 1960), laser ngày càng tạo ra nhiều đột phá 
trong khoa học, kĩ thuật và công nghệ. Khi laser xung cực ngắn, cường độ cao tương tác với 
vật chất, một trong những hiệu ứng quang phi tuyến xảy ra là sự phát xạ sóng điều hòa bậc 
cao (High-order Harmonic Generation – viết tắt là HHG), tức là phát ra sóng HHG có tần số 
bằng số nguyên lần tần số của laser chiếu vào) (Lewenstein, Balcou, Ivanov, & Huillier, 
1994). Phổ HHG có dạng đặc trưng với ba vùng rõ rệt: (i) đầu tiên là vùng nhiễu loạn ở vùng 
tần số thấp, tại đó cường độ HHG giảm nhanh; (ii) sau đó là miền phẳng trải dài trên một 
miền của tần số, ở đó, cường độ HHG được giữ ổn định; (iii) cuối cùng, miền phẳng kết thúc 
tại điểm dừng, sau đó, cường độ HHG giảm nhanh đột ngột. 
 HHG có nhiều ứng dụng quan trọng như thu nhận thông tin cấu trúc nguyên tử, phân 
tử (Baker et al., 2006; Haessler et al., 2015); thăm dò động lực học của electron (Zhang, Yu, 
Chen, Jiang, & Sun, 2015) và hạt nhân (Jin et al., 2012); chụp ảnh cắt lớp orbital lớp ngoài 
cùng (Highest-Occupied Molecular Orbital – viết tắt là HOMO) của phân tử (Itatani et al., 
Cite this article as: Tran Cong Minh, Truong Quan Hao, Tran Phuc Khang, Le Thi Cam Tu, & 
Phan Thi Ngoc Loan (2021). Tomography of partially aligned N2 molecules from high-order harmonic 
generation. Ho Chi Minh City University of Education Journal of Science, 18(6), 1085-1099. 
 1085 
Tạp chí Khoa học Trường ĐHSP TPHCM Tập 18, Số 6 (2021): 1085-1099 
2004, Qin, & Zhu, 2017). Trong đó, phương pháp chụp ảnh cắt lớp HOMO phân tử lần đầu 
tiên được thực hiện bởi Itatani và các cộng sự (Itatani et al., 2004) từ HHG đo đạc từ thực 
nghiệm cho phân tử N2. Sau đó, các tác giả (Le, Le, Xie, & Lin, 2007) đã bằng lí thuyết, 
chụp ảnh cắt lớp cho phân tử đối xứng như N2 và O2. Các tác giả (Le et al., 2007) đã chỉ ra 
những hạn chế của quy trình chụp ảnh cắt lớp của Itatani (Itatani et al., 2004), và đồng thời, 
đề xuất rằng, để nâng cao hiệu quả của hình ảnh tái tạo HOMO, nên sử dụng laser có bước 
sóng dài. Bên cạnh đó, một số các công trình đã phát triển phương pháp để khắc phục những 
khuyết điểm của mô hình được đề xuất bởi Itatani, như sử dụng hàm sóng tán xạ thay vì sóng 
phẳng của electron ở vùng liên tục (Zhai et al., 2016). Sau đó, phương pháp chụp ảnh cắt lớp 
đã được ứng dụng khi HHG phát xạ khi tương tác với laser hai màu (Zhai et al., 2018). Gần 
đây, phương pháp chụp ảnh cắt lớp đã được mở rộng cho phân tử bất đối xứng CO (Qin, 
Zhu, Zhang, & Lu, 2012; Chen, Fu, & Liu, 2013; Xie, Yu, Li, Wang, & Chen, 2018; Zhai et 
al., 2018; Yuan et al., 2018). 
 Theo quy trình chụp ảnh cắt lớp HOMO của phân tử, đầu tiên, các phân tử cần phải 
được định phương trước khi tương tác với laser mạnh để phát ra HHG, nhằm tránh hiệu ứng 
trung bình (Itatani et al., 2004). Trong các công trình trước đây, các phân tử được giả thuyết 
là định phương hoàn toàn trong quá trình phát xạ HHG (Itatani et al., 2004; Le et al., 2007; 
Qin et al., 2012; Chen et al., 2013; Zhai et al., 2018; Yuan et al., 2018). Tuy nhiên, trong 
thực tế, các phân tử chỉ có thể định phương một phần (Zhou, Tong, Zhao, & Lin, 2005; Qin, 
& Zhu, 2017). Đại lượng đặc trưng cho chất lượng định phương của một khối khí phân tử 
được gọi là mức độ định phương. Các kĩ thuật định phương hiện nay được ứng dụng trong 
thực nghiệm sử dụng phương pháp va chạm (Pullman, Friedrich, & Herschbach, 1990; 
Aquilanti et al., 1994), phương pháp trường điện tĩnh (Cho, & Be ... g đến điểm dừng của phổ HHG, tại bậc 
99, phù hợp bậc 97 theo định luật điểm dừng IUpp+ 3. 17 , với U p là thế trọng động. Tuy 
nhiên, mức độ định phương ảnh hưởng đến cường độ HHG và vị trí điểm cực tiểu trong phổ 
HHG. Cụ thể, khi mức độ định phương giảm, cường độ HHG giảm, điểm giao thoa cực tiểu 
dịch về phía bậc HHG cao. Nguyên nhân là do khi mức độ định phương giảm, đóng góp của 
HHG gây ra bởi các góc  lớn trở lên đáng kể, làm ảnh hưởng đến cường độ và cấu trúc 
phổ HHG. 
 1092 
Tạp chí Khoa học Trường ĐHSP TPHCM Trần Công Minh và tgk 
 Hình 3. Cường độ HHG song song (a) và vuông góc (b) với các mức độ định phương 
 khác nhau, khi  = 300 . Xung laser với bước sóng 1200 nm, cường độ 2×1014 W/cm2, 
 độ dài xung 11 chu kì quang học được sử dụng 
 Từ phổ HHG, chúng tôi tách lưỡng cực dịch chuyển theo phương song song và vuông 
góc theo công thức (13). Hình 4 biểu diễn độ lớn của lưỡng cực dịch chuyển trong hệ tọa độ 
gắn với phòng thí nghiệm cho giá trị k 2 =0.,. 13 13 96 , tức sử dụng các bậc HHG trong 
vùng miền phẳng từ bậc 17 đến điểm dừng – bậc 99. Kết quả cho thấy khi phân tử định 
phương hoàn toàn, cos2 = 1, lưỡng cực dịch chuyển phụ thuộc mạnh vào k 2 . Tuy nhiên, 
khi giảm dần mức độ định phương, độ lớn của lưỡng cực dịch chuyển thay đổi, và tiến dần 
về 0. Sự giảm dần về 0 ngụ ý rằng, lưỡng cực dịch chuyển mất dần tính cấu trúc theo , 
tức theo năng lượng; tiên đoán sự mất dần cấu trúc trong không gian đảo của nó, tức không 
gian tọa độ. Như vậy, mức độ định phương phân tử ảnh hưởng đến lưỡng cực dịch chuyển, 
do đó, dự đoán sẽ ảnh hưởng đến hình ảnh chụp cắt lớp của HOMO của phân tử. 
 Hình 4. Lưỡng cực dịch chuyển của phân tử N2 với mức độ định phương khác nhau. 
 Góc định phương là  = 300 . Laser có thông số như trên Hình 3 được sử dụng 
 1093 
Tạp chí Khoa học Trường ĐHSP TPHCM Tập 18, Số 6 (2021): 1085-1099 
 Hình 5. HOMO của phân tử N2 được tái tạo từ HHG định phương không hoàn toàn 
 với mức độ định phương khác nhau 
 Với lưỡng cực dịch chuyển gắn với hệ quy chiếu phòng thí nghiệm thu được từ HHG 
“thực nghiệm”, chúng tôi dùng phép quay để chuyển chúng về hệ quy chiếu gắn với phân tử, 
sau đó dùng phép biến đổi Fourier ngược để thu được hàm sóng (xem phương trình (14)). Hình 
ảnh HOMO phân tử N2 được tái tạo từ HHG với mức độ định phương khác nhau được trình 
bày trên Hình 5. Hình 5(a) thể hiện hình ảnh mô phỏng HOMO của khối khí phân tử N2 được 
định phương hoàn toàn. Chúng tôi nhận thấy, HOMO của N2 có cấu trúc ba thùy rõ rệt, phù 
hợp với kết quả các công trình công bố trước đây (Itatani et al., 2004; Le et al., 2007; Qin, 
& Zhu, 2017)]. Hình 5(b)-5(d) thể hiện hình ảnh HOMO của phân tử N2 khi mức độ định 
phương giảm dần. Ở Hình 5(a)-5(b), khi mức độ định phương cao, chúng tôi vẫn có thể nhìn 
thấy rõ các thùy của phân tử N2. Tuy nhiên, khi giảm mức độ định phương, sự tương phản 
giữa các thùy giảm càng rõ rệt. Ở Hình 5(c) và 5(d), với mức độ định phương thấp, chúng 
tôi không còn thấy rõ hai thùy của phân tử N2. Lúc này, hình ảnh HOMO của phân tử gần 
giống như orbital của nguyên tử, tức phân bố của đám mây electron không còn phụ thuộc 
vào góc cực. Điều này có thể giải thích là do khi khối khí được định phương kém, thì hiệu 
ứng trung bình làm mất đi tính cấu trúc của phổ HHG, và lưỡng cực dịch chuyển. Do đó, sử 
dụng HHG trung bình hóa bị mất tính cấu trúc, sẽ không còn phù hợp để chụp ảnh cắt lớp 
HOMO của phân tử. Chúng tôi kết luận rằng, với mức độ định phương đạt được trong phòng 
thí nghiệm hiện nay (~0.8), thì cấu trúc của HOMO của phân tử vẫn có thể được tái tạo từ 
phổ HHG với chất lượng tốt. Tuy nhiên, khi mức độ định phương thấp, không còn thu nhận 
được HOMO phân tử. Chúng tôi nhận thấy mức độ định phương giới hạn để hình ảnh thu 
được vẫn còn thấy rõ hai thùy của phân tử N2 là 0.50. 
 1094 
Tạp chí Khoa học Trường ĐHSP TPHCM Trần Công Minh và tgk 
3.3. Sử dụng gần đúng bằng hàm giải tích mô tả hàm phân bố định phương 
 Ngoài việc sử dụng hàm phân bố định phương thu được bằng cách giải chính xác bằng 
số TDSE (xem mục 2.1), trong nhiều công trình như (Lein et al., 2005; Kraus et al., 2014; 
Yu et al., 2017), các tác giả sử dụng gần đúng bằng hàm giải tích để mô tả chúng. Sử dụng 
gần đúng bằng hàm giải tích cho phép tính toán nhanh, tiết kiệm thời gian và tài nguyên tính 
toán, và cho phép đưa ra các kết luận cả về mặt định tính và định lượng về ảnh hưởng của 
mức độ định phương lên các hiệu ứng vật lí trường mạnh (Lein et al., 2005). Trong tiểu mục 
này, chúng tôi kiểm tra xem, liệu rằng việc sử dụng gần đúng bằng hàm phân bố giải tích 
(Lein et al., 2005) có ảnh hưởng đến kết luận về ảnh hưởng của chất lượng định phương đến 
hình ảnh HOMO tái tạo từ HHG của khối khí phân tử N2 định phương không hoàn toàn. 
 Hàm phân bố định phương được mô tả gần đúng bằng hàm giải tích như sau 
  1
 ( ) = A, (15) 
  +1 22 
 2 ln − cos
  −1
trong đó, tham số  1 để kiểm soát hàm phân bố và mức độ định phương (Lein et al., 
2005). Khi  =1, các phân tử được định phương hoàn toàn. A là hệ số chuẩn hóa. 
 Hình 6. Phân bố định phương của hàm giải tích (nét đứt) và 
 hàm chính xác từ TDSE (nét liền) cho hai mức độ định phương 0.73 và 0.50 
 Để so sánh trực quan hàm phân bố định phương giải tích (15), và phân bố định phương 
giải chính xác từ TDSE (mục 2.1), trên Hình 6, chúng tôi biểu diễn chúng cho hai trường 
hợp mức độ định phương cos2 = 0.73 và cos2 = 0.50 . Kết quả cho thấy, hai cách 
biểu diễn hàm phân bố (gần đúng và chính xác) dạng và độ lớn tương tự nhau. Sự tương tự 
này sẽ dẫn đến sự tương tự về HHG, và lưỡng cực dịch chuyển khi sử dụng hai cách biểu 
diễn khác nhau của hàm phân bố. 
 Cuối cùng, chúng tôi sử dụng HHG phát ra từ phân tử N2 định phương không hoàn 
toàn, mà sự định phương được mô tả bằng hàm giải tích gần đúng, để tái tạo hình ảnh HOMO. 
 1095 
Tạp chí Khoa học Trường ĐHSP TPHCM Tập 18, Số 6 (2021): 1085-1099 
Kết quả được biểu diễn trên Hình 7, và so sánh với trường hợp hàm định phương được giải 
chính xác từ TDSE. Kết quả cho thấy, với cùng một mức độ định phương, về mặt định tính, 
chất lượng hình ảnh HOMO tái tạo được từ HHG với hai cách mô tả hàm định phương khác 
nhau, là tương đương nhau. Để phân tích định lượng, trên Hình 8, chúng tôi trình bày ảnh 
chụp lát cắt hàm sóng cho các trường hợp y =−0.5, y = 0 , y = 0.5 khi so sánh hai cách mô 
tả định phương ở các mức độ định phương lần lượt là cos2  = 0.50 , và cos2  = 0.73. 
Kết quả cho thấy, mặc dù sử dụng cách mô tả hàm phân bố định phương khác nhau, nhưng 
lát cắt của HOMO giống nhau. Như vậy, chúng tôi kết luận rằng mô tả định phương phân tử 
gần đúng bằng hàm giải tích, vẫn cho kết quả chính xác về mặt định tính và định lượng. 
 Hình 7. So sánh HOMO của phân tử N2 với các mức độ định phương khác nhau. 
 Sự định phương của phân tử được mô tả gần đúng bằng hàm giải tích [(a) – (b)], 
 và hàm chính xác từ TDSE [(c) - (d)] 
 Hình 8. Lát cắt tại :(a) y =−05. , (b) y = 0, (c) y = 05. 
của HOMO phân tử N2 với các mức độ định phương khác nhau. Sự định phương của phân tử 
 được mô tả gần đúng bằng hàm giải tích [(a) – (b)], và hàm chính xác từ TDSE [(c) - (d)] 
 1096 
Tạp chí Khoa học Trường ĐHSP TPHCM Trần Công Minh và tgk 
4. Kết luận 
 Trong bài báo này, chúng tôi đã khảo sát ảnh hưởng của sự định phương không hoàn 
toàn lên hình ảnh HOMO tái tạo được từ phổ HHG. Kết quả cho thấy, sự định phương ảnh 
hưởng rõ rệt đến chất lượng hình ảnh HOMO. Mức độ định phương giảm dẫn đến giảm sự 
tương phản, tức làm mất đi tính cấu trúc của hình ảnh HOMO. Khi mức độ định phương nhỏ 
hơn 0.5, hình ảnh HOMO của phân tử N2 không thể hiện được cấu trúc của phân tử, mà gần 
có đối xứng cầu tương tự như nguyên tử. Cuối cùng, chúng tôi kết luận rằng sử dụng gần 
đúng bằng hàm giải tích để mô tả hàm định phương phân tử vẫn cho kết quả đáng tin cậy, 
và giảm được khối lượng tính toán so với giải chính xác từ TDSE. 
 ❖ Tuyên bố về quyền lợi: Các tác giả xác nhận hoàn toàn không có xung đột về quyền lợi. 
 ❖ Lời cảm ơn: Nghiên cứu này được tài trợ bởi đề tài cơ sở trọng điểm của Trường Đại học 
 Sư phạm Thành phố Hồ Chí Minh, mã số CS2020.19.05TĐ. 
 TÀI LIỆU THAM KHẢO 
Aquilanti, V., Ascenzi, D., Cappelletti, D., & Pirani, F. (1994). Velocity dependence of collisional 
 alignment of oxygen molecules in gaseous expansions. Nature, 371, 399-402. 
Baker, S., Robinson, J. S., Haworth, C. A., Teng, H., Smith, R. A., Chirilǎ, C. C., Marangos, J. P. 
 (2006). Probing proton dynamics in molecules on an attosecond time scale. Science, 
 312(5772), 424-427. 
Chen, Y. J., Fu, L. B., & Liu, J. (2013). Asymmetric Molecular Imaging through Decoding Odd-
 Even High-Order Harmonics. Physical Review Letters, 111(7), 073902. 
Cho, V. A., & Bernstein, R. B. (1991). Tight focusing of beams of polar polyatomic molecules via 
 the electrostatic hexapole lens. Journal of Physical Chemistry, 95(21), 8129-8136. 
De, S., Znakovskaya, I., Ray, D., Anis, F., Johnson, N. G., Bocharova, I. A., & Kling, M. F. (2009). 
 Field-Free Orientation of CO Molecules by Femtosecond Two-Color Laser Fields. Physical 
 Review Letters, 103(15), 153002. 
Friedrich, B., & Herschbach, D. R. (1991). On the possibility of orienting rotationally cooled polar 
 molecules in an electric field. Zeitschrift Für Physik D Atoms, Molecules and Clusters, 18(2), 
 153-161. 
Frisch, Æ., Plata, R. E., & Singleton, D. A. (2009). Gaussian 09W Reference. J. Am. Chem. Soc., 
 137, 3811-3826. 
Haessler, S., Caillat, J., Boutu, W., Ruchon, T., Diveki, Z., Breger, P., & Ruchon, T. (2015). 
 Attosecond imaging of molecular electronic wave-packets. Nature Physics, 200-206. 
Itatani, J., Levesque, J., Zeidler, D., Niikura, H., Pépin, H., Kieffer, J. C., & Villeneuve, D. M. 
 (2004). Tomographic imaging of molecular orbitals. Nature, 432(7019), 867-871. 
Jin, C., Bertrand, J. B., Lucchese, R. R., Wörner, H. J., Corkum, P. B., Villeneuve, D. M., & Lin, 
 C. D. (2012). Intensity dependence of multiple orbital contributions and shape resonance in 
 high-order harmonic generation of aligned N2 molecules. Physical Review A, 85(1), 013405. 
 1097 
Tạp chí Khoa học Trường ĐHSP TPHCM Tập 18, Số 6 (2021): 1085-1099 
Kak, A. C., & Slaney, M. (2001). Principles of Computerized Tomographic Imaging. Society for 
 Industrial and Applied Mathemathics, New York. 
Kraus, P. M., Baykusheva, D., & Wörner, H. J. (2014). Two-pulse field-free orientation reveals 
 anisotropy of molecular shape resonance. Physical Review Letters, 113(2), 023001. 
Le, V.-H., Le, A.-T., Xie, R.-H., & Lin, C. D. (2007). Theoretical analysis of dynamic chemical 
 imaging with lasers using high-order harmonic generation. Physical Review A, 76(1), 013414. 
Lein, M., De Nalda, R., Heesel, E., Hay, N., Springate, E., Velotta, R., & Marangos, J. P. (2005). 
 Signatures of molecular structure in the strong-field response of aligned molecules. Journal of 
 Modern Optics, 52(2-3), 465-478. 
Lewenstein, M., Balcou, P., Ivanov, M. Y., & Huillier, A. L. (1994). Theory of high-harmonic 
 generation by low-frequency laser fields. Physical Review A, 49(3), 2117-2132. 
Lin, C. D., Le, A. T., Jin, C., & Wei, H. (2018). Attosecond and Strong-Field Physics: Principles and 
 Applications. In Cambridge University Press. 
Maiman, T. H. (1960). Stimulated Optical Radiation in Ruby. Nature, 187(4736), 493-494. 
Pullman, D. P., Friedrich, B., & Herschbach, D. R. (1990). Facile alignment of molecular rotation in 
 supersonic beams. The Journal of Chemical Physics, 93(5), 3224-3236. 
Qin, M., & Zhu, X. (2017). Molecular orbital imaging for partially aligned molecules. Optics and 
 Laser Technology, 87, 79–86. 
Qin, M., Zhu, X., Zhang, Q., & Lu, P. (2012). Tomographic imaging of asymmetric molecular 
 orbitals with a two-color multicycle laser field. Optics Letters, 37(24), 5208. 
Seideman, T. (1995a). On the selection of magnetic states in angle-resolved photodissociation. The 
 Journal of Chemical Physics, 102(16), 6487-6498. 
Seideman, T. (1995b). On the selection of magnetic states in angle‐resolved photodissociation. The 
 Journal of Chemical Physics, 102(16), 6487-6498. 
Stapelfeldt, H., & Seideman, T. (2003). Colloquium: Aligning molecules with strong laser pulses. 
 Rewiews of Modern Physics, 75, 543-557. 
Xie, X., Yu, S., Li, W., Wang, S., & Chen, Y. (2018). Routes of odd-even harmonic emission from 
 oriented polar molecules. Optics Express, 26(14), 18578. 
Yu, S. J., Li, W. Y., Li, Y. P., & Chen, Y. J. (2017). Probing degrees of orientation of top molecules 
 with odd-even high-order harmonics. Physical Review A, 96(1), 013432. 
Yuan, H., He, L., Wang, F., Wang, B., Zhu, X., Lan, P., & Lu, P. (2018). Tomography of asymmetric 
 molecular orbitals with a one-color inhomogeneous field. Optics Letters, 43(4), 931. 
Zhai, C., He, L., Lan, P., Zhu, X., Li, Y., Wang, F.,& Lu, P. (2016). Coulomb-corrected molecular 
 orbital tomography of nitrogen. Scientific Reports, 6, 23236. 
Zhai, C., Zhang, X., Zhu, X., He, L., Zhang, Y., Wang, B., & Lu, P. (2018). Single-shot molecular 
 orbital tomography with orthogonal two-color fields. Optics Express, 26(3), 314573. 
Zhang, B., Yu, S., Chen, Y., Jiang, X., & Sun, X. (2015). Time-resolved dynamics of odd and even 
 harmonic emission from oriented asymmetric molecules. Physical Review A, 92(5), 053833. 
Zhou, X., Tong, X. M., Zhao, Z. X., & Lin, C. D. (2005). Alignment dependence of high-order 
 harmonic generation from N2 and O2 molecules in intense laser fields. Physical Review A - 
 Atomic, Molecular, and Optical Physics, 72(3), 033412. 
 1098 
Tạp chí Khoa học Trường ĐHSP TPHCM Trần Công Minh và tgk 
 TOMOGRAPHY OF PARTIALLY ALIGNED N2 MOLECULES 
 FROM HIGH-ORDER HARMONIC GENERATION 
 Tran Cong Minh1, Truong Quan Hao1, Tran Phuc Khang1, 
 Le Thi Cam Tu2, Phan Thi Ngoc Loan1* 
 1Ho Chi Minh City University of Education, Vietnam 
 2Ton Duc Thang University, Vietnam 
 *Corresponding author: Phan Thi Ngoc Loan – Email: loanptn@hcmue.edu.vn 
 Received: January 18, 2021; Revised: April 22, 2021; Accepted: June 08, 2021 
ABSTRACT 
 Using the molecular tomography method, we reconstruct the highest-occupied molecular 
orbital (HOMO) from the high-order harmonic generation (HHG) emitted from N2 molecules when 
considering the alignment effect. We utilize two different approaches to describe the alignment 
distribution – (i) exactly by numerically solving the time-dependent Schrӧdinger equation and (ii) by 
an approximately analytical function. The results show that when lowering the degree of alignment, 
the accuracy of the reconstructed molecular HOMO decreases. When the alignment degree is less 
than 0.5, the HOMO cannot be reconstructed exactly. Also, the two different approaches of the 
alignment distribution offer the same results. 
 Keywords: high-order harmonic generation; N2 molecules; partially alignment; tomography 
 1099