Các trạng thái đan rối trong bộ ghép phi tuyến kiểu Kerr được bơm trên hai mode
Bài báo này, chúng tôi nghiên cứu bộ ghép phi tuyến kiểu Kerr bao gồm hai dao động tử phi tuyến được liên kết bằng kiểu tương tác tuyến tính và chịu tác động của trường điện từ bên ngoài được giả thiết dưới dạng các xung liên tục trên cả hai mode. Chúng tôi sẽ chỉ ra rằng hệ có thể được xem như kéo lượng tử phi tuyến và đóng vai trò như một mô hình hai qubit. Bằng cách sử dụng các công thức toán tử biến đổi, chúng tôi tiến hành mô hình hóa hệ lượng tử, tìm ra biểu thức giải tích của biên độ xác suất của các trạng thái phụ thuộc vào thời gian và từ đó tạo ra các trạng thái đan rối cực đại với hiệu quả cao.

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5
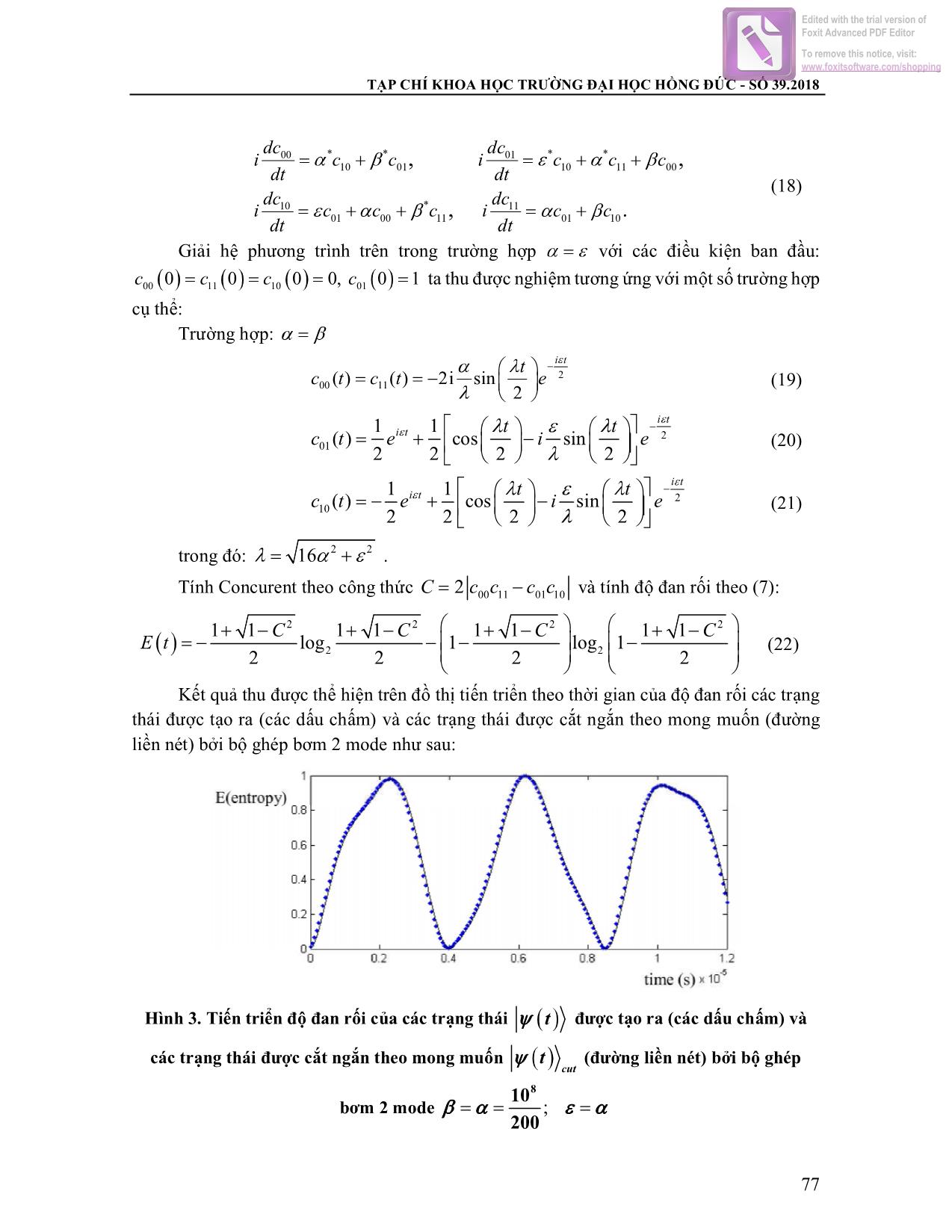
Trang 6
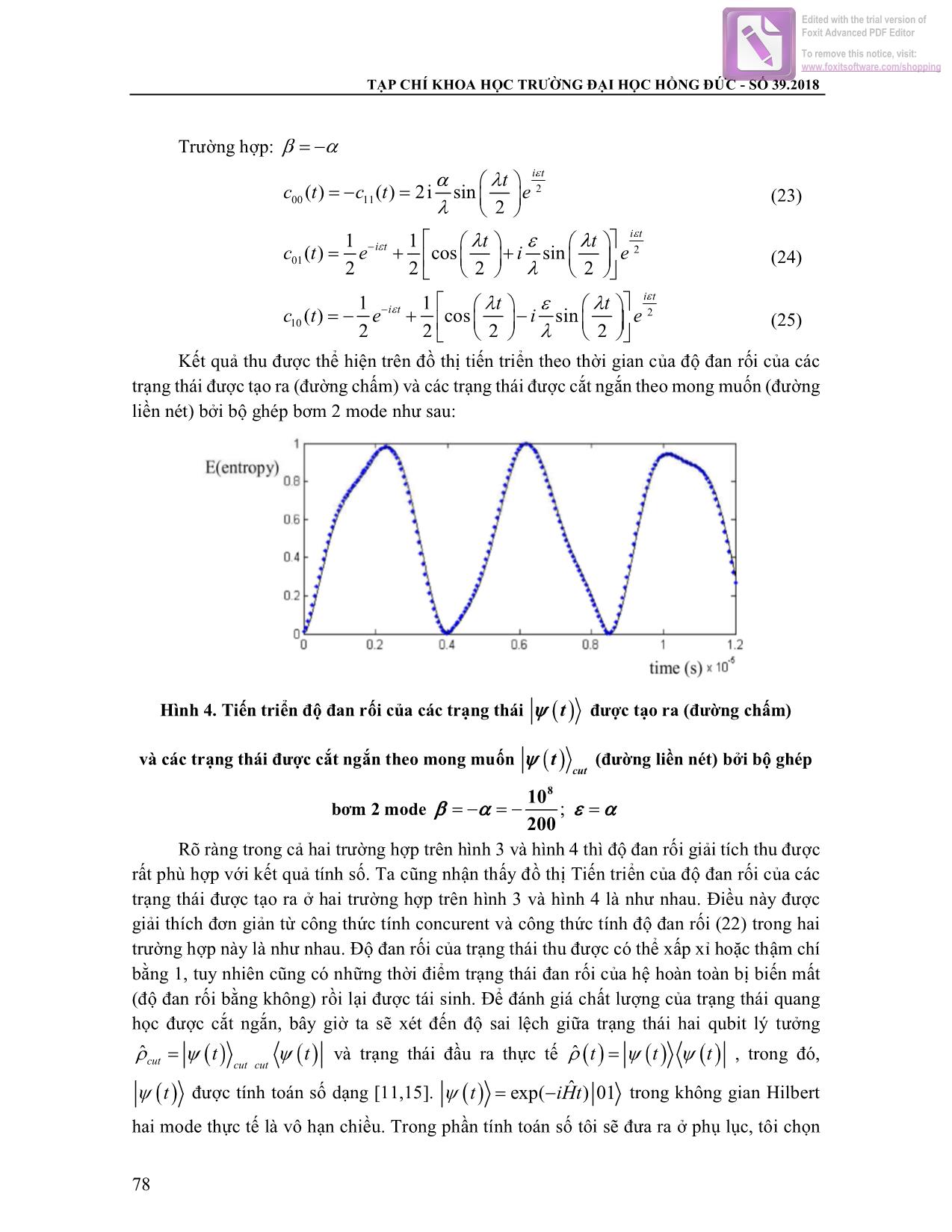
Trang 7
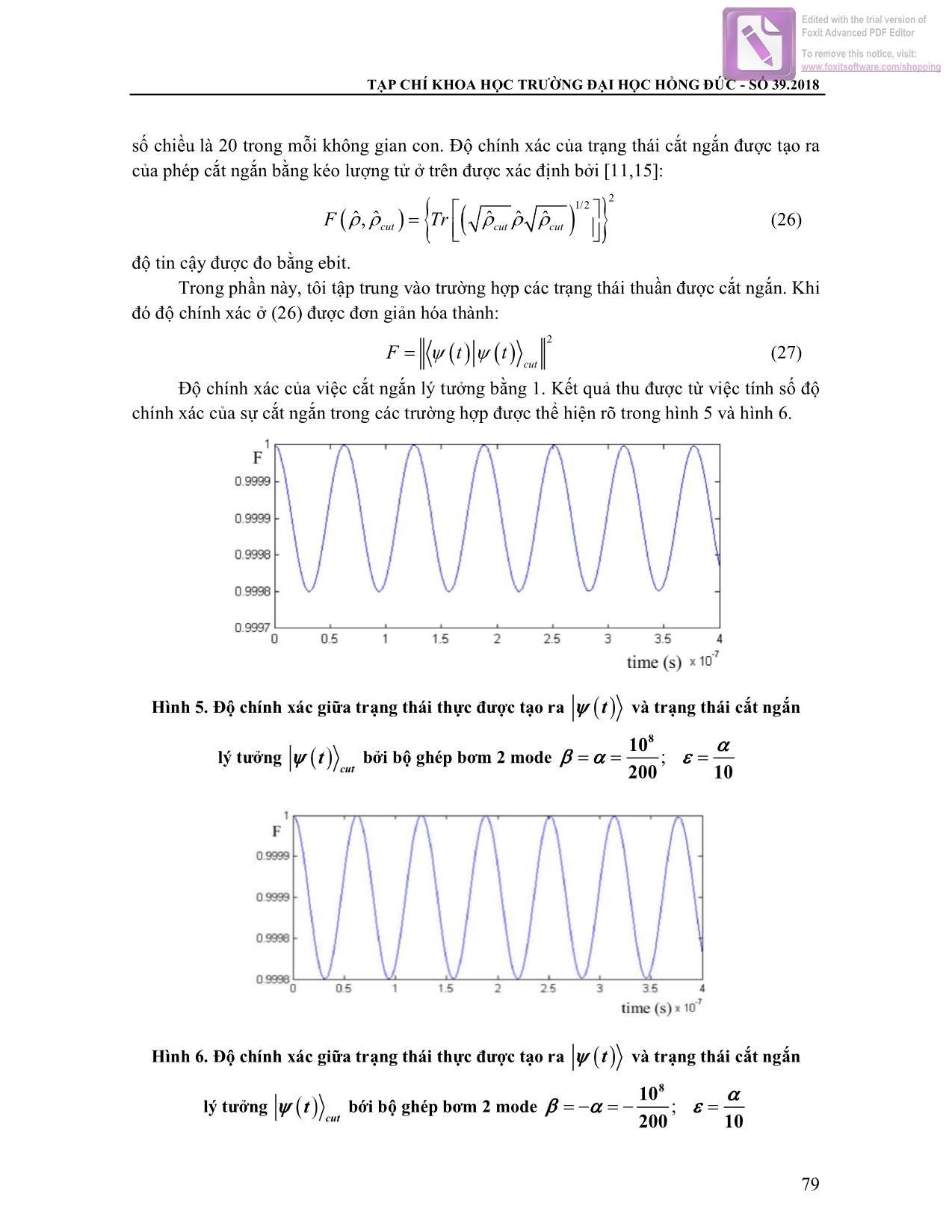
Trang 8

Trang 9

Trang 10
Bạn đang xem tài liệu "Các trạng thái đan rối trong bộ ghép phi tuyến kiểu Kerr được bơm trên hai mode", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Các trạng thái đan rối trong bộ ghép phi tuyến kiểu Kerr được bơm trên hai mode

TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 72 CÁC TRẠNG THÁI ĐAN RỐI TRONG BỘ GHÉP PHI TUYẾN KIỂU KERR ĐƯỢC BƠM TRÊN HAI MODE Nguyễn Thị Hồng1 TÓM TẮT Bài báo này, chúng tôi nghiên cứu bộ ghép phi tuyến kiểu Kerr bao gồm hai dao động tử phi tuyến được liên kết bằng kiểu tương tác tuyến tính và chịu tác động của trường điện từ bên ngoài được giả thiết dưới dạng các xung liên tục trên cả hai mode. Chúng tôi sẽ chỉ ra rằng hệ có thể được xem như kéo lượng tử phi tuyến và đóng vai trò như một mô hình hai qubit. Bằng cách sử dụng các công thức toán tử biến đổi, chúng tôi tiến hành mô hình hóa hệ lượng tử, tìm ra biểu thức giải tích của biên độ xác suất của các trạng thái phụ thuộc vào thời gian và từ đó tạo ra các trạng thái đan rối cực đại với hiệu quả cao. Từ khóa: Trạng thái đan rối, độ đan rối lượng tử, entropy von Neumann, concurrence, cổng lượng tử. 1. ĐẶT VẤN ĐỀ Do nhu cầu tính toán ngày càng tăng, máy tính được vi tính hóa liên tục kèm theo đó là nhu cầu cải tiến thiết bị điện tử ngày càng nhỏ hơn nữa. Việc thực hiện cả hai nhu cầu trên là thách thức lớn đối với các nhà khoa học. Trong khoảng đầu những năm tám mươi của thế kỷ trước, để tìm lối thoát khỏi tình huống này, nhà bác học nổi tiếng Richard Feynman đã đưa ra ý tưởng tính toán chính ngay trên hệ vật lý [2]. Sau đó, tính toán lượng tử đã phát triển như vũ bão, hiện đang là đề tài nóng trong vật lý lý thuyết. Thông tin lượng tử dùng đơn vị nhỏ nhất là qubit (bit lượng tử), một hệ hai trạng thái bất kỳ để liên hệ với tin học cổ điển, người ta thường ký hiệu chúng là 0 và 1 . Trong khuôn khổ lý thuyết lượng tử, nó có thể là tổ hợp tuyến tính của hai trạng thái 0 và 1 . Theo đó thì qubit là một véc tơ trong không gian Hilbert hai chiều được biểu diễn dưới dạng [1]: 0 1= +a b (1) Trong đó a và b là các số phức thỏa mãn điều kiện chuẩn hóa 2 2 1+ =a b . Biểu hiện của qubit khi được đo là chỉ thu được các kết quả 0 hoặc 1 . Phép đo làm thay đổi trạng thái của qubit, làm tan vỡ trạng thái tổ hợp của 0 và 1 . Khi không thực hiện một phép đo nào lên trạng thái lượng tử, rõ ràng nó giữ nguyên tất cả các biến liên tục mô tả hệ như a và b. Nhưng nếu không đo thì làm sao có thể xử lý được thông tin? Khái 1 Giảng viên khoa Khoa học Tự nhiên, Trường Đại học Hồng Đức Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 73 niệm trạng thái đan rối được đưa ra giải quyết cho câu hỏi này, đó là trạng thái không thể phân ra được tích tenxơ của hai trạng thái mô tả các hệ con thành phần. Nếu trạng thái của hệ là đan rối thì khi đọc qubit riêng biệt thứ nhất được hai kết quả với cùng xác suất thì nếu ta đo qubit thứ hai cũng luôn thu được kết quả như qubit thứ nhất (thậm chí ở khoảng cách rất xa). Einstein đã gọi đây là một tác động ma quái ở khoảng cách. Trạng thái đan rối của hai hệ con được định nghĩa là trạng thái được mô tả bằng một véctơ trong không gian Hilbert của hệ phức hợp mà không phải là tích của các véctơ mô tả các hệ con. A B¹ Ä (2) Toán tử ma trận mật độ của chúng không được biểu diễn dưới dạng: =å A Bi i i i p (3) Ma trận mật độ là đại lượng đo mật độ trạng thái nên không có thứ nguyên. Một lớp các trạng thái đan rối này được gọi là các trạng thái Bell. Tính chất đan rối của hệ lượng tử tiến tới thực hiện một máy tính lượng tử trong tương lai với những khả năng tính toán mà không một máy tính hiện thời nào thực hiện được [3,4]. Trong bài báo này, chúng tôi nghiên cứu sử dụng kéo lượng tử để cắt các không gian Hilbert vô hạn chiều tạo ra các trạng thái đan rối giữa hai qubit có độ đan rối cao nhất - Trạng thái Bell. Hình thức luận kéo lượng tử và mô hình kéo lượng tử tuyến tính. Chúng ta biết rằng không gian Hilbert là một không gian mà không bị giới hạn về số chiều, đó là một không gian có tích vô hướng. Tuy nhiên, gần đây các trạng thái liên kết hữu hạn chiều đã được xem xét ở các khía cạnh khác nhau trong một số công trình. Có nhiều các trạng thái lượng tử hữu hạn chiều như trạng thái n-photon, các trạng thái bị ép hữu hạn chiều, các trạng thái Bell... Các trạng thái này được gọi là các trạng thái bị cắt [7,8,10]. Chúng thường được xét trong trạng thái đan rối lượng tử. Ví dụ trạng thái Bell là một trạng thái như vậy [13]. Kéo lượng tử tuyến tính chính là cơ cấu sử dụng các phần tử tuyến tính cắt các không gian vô hạn chiều thành không gian hữu hạn chiều. Từ đó ta tìm ra các hệ liên quan trong tin học lượng tử. Đề án lý thuyết đầu tiên về khả năng cắt ngắn các trạng thái liên kết quang được đề xuất bởi Pegg, Philips, và Barnett [5,12,14]. Các trạng thái kết hợp định nghĩa không gian hai chiều: 2 0 0 exp 2 ! ¥ ¥ = = æ ö ç ÷= = - ç ÷ è ø å å n n n n a n n (4) đã được cắt để có một dạng đơn giản hơn mà ở đó chỉ có sự chồng chập của hai trạng thá ... + + ed b bb (5) Độ đan rối của trạng thái cắt ngắn được tính thông qua độ tụ hợp (concurrence) Concurrence của trạng thái đang xét được xác định theo [13]: 00 11 01 102= = -%AB AB ABC c c c c (6) Cũng theo [13] ta xác định độ đan rối AB E của AB theo công thức: 2 2log 1 log 1= - - - -ABE x x x x (7) với 21 1 2 + - = C x . Trong đó Concurent có thứ nguyên là ebit, độ đan rối được đo bằng entropy. 2. KÉO LƯỢNG TỬ PHI TUYẾN VÀ BỘ GHÉP PHI TUYẾN KIỂU KERR Kéo lượng tử phi tuyến là thiết bị quang học sử dụng các yếu tố quang phi tuyến mà kết quả tác động của nó lên các trạng thái quang cũng tương tự như mô tả đối với trường hợp kéo lượng tử tuyến tính. Trong phần này, chúng tôi sẽ mô tả thiết bị kéo lượng tử phi Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 75 tuyến sử dụng bộ ghép hai dao động phi tuyến với tính chất phi tuyến Kerr ,a b có tính đến cả tương tác với trường ngoài. Bộ ghép phi tuyến kiểu Kerr thể hiện sự tự khắc phục, tự điều chế những thay đổi của chính nó và các hiệu ứng tự chuyển đổi. Trong trạng thái lượng tử, chúng cũng tạo ra ánh sáng nén, hay các trạng thái đan rối [6]. Bộ nối phi tuyến kiểu Kerr được đưa ra bao gồm hai dao động tử điều hòa phi tuyến kiểu Kerr a và b tương tác với nhau bằng kiểu tương tác tuyến tính, các dao động tử có thể được tác động bằng trường điện từ bên ngoài được giả thiết dưới dạng xung liên tục mô tả trên hình 2. Cụ thể, chúng tôi sẽ giới thiệu bộ nối phi tuyến kiểu Kerr bao gồm hai dao động tử điều hòa phi tuyến kiểu Kerr a và b được liên kết một cách tuyến tính với nhau, các dao động tử được tác động bằng trường điện từ bên ngoài được giả thiết dưới dạng các xung liên tục [11]. Hình 2. Mô hình bộ ghép phi tuyến kiểu Kerr, tương tác với nhau và chịu sự kích thích của trường ngoài ở cả hai mode dưới dạng xung liên tục Hamiltonian mô tả hệ có dạng: 0 1 ˆ ˆ ˆ= +H H H (8) trong đó: 0 ˆ ˆˆ ˆ ˆ+ += +a bH a a b b (9) 1 int ex ex ˆ ˆ ˆ ˆ ˆ ˆ= + + + +a b a bnonl nonl t tH H H H H H (10) 22 2 2ˆ ˆˆ ˆ ˆ ˆ 2 2 + ++ = +a b a bnonl nonlH H a a b b (11) * int ˆ ˆˆ ˆ ˆ+ += +H a b ab (12) * * ex ex ˆ ˆˆ ˆˆ ˆ;+ += + = + a b t tH a a H b b (13) Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 76 ˆ ˆˆ ˆ, , ,+ +a b a b là các toán tử hủy và sinh boson tương ứng với hai mode a và b của tần số ,a b ; intHˆ mô tả tương tác tuyến tính giữa các dao động tử, đặc trưng bằng tham số mô tả độ lớn của tương tác giữa các mode, , ex ˆ a b tH mô tả tác động của xung bơm bên ngoài lên các dao động tử điều hòa a và b, các xung bơm này là các xung bơm liên tục. ,a b là độ cảm mô tả tính chất phi tuyến trong Hamiltonian của các dao động tử. Các tham số , đặc trưng cho độ mạnh của tương tác với trường ngoài. Tiến triển theo thời gian của hệ có thể được mô tả bởi phương trình Schrodinger: ˆ= d i t H t dt (14) Bỏ qua quá trình tắt dần (damping) và do đó tiến triển của hệ có thể được mô tả bởi một hàm sóng phụ thuộc thời gian. Hàm sóng này có thể được biểu diễn thông qua tổ hợp tuyến tính trong cơ sở của các trạng thái Fock như sau: , 0 ( ) ( ) ¥ = = å mn a b m n t c t m n (15) Với ( )mnc t là biên độ xác suất tương ứng với trạng thái m và n photon trên dao động tử a và b. Sử dụng các tính chất của toán tử hủy hạt và toán tử sinh hạt và kết hợp các biểu thức từ (11) đến (13) thay vào phương trình (14) ta thu được: * 1, 1 1, 1 * * 1, 1, , 1 , 1 1 1 1 2 1 1 + c 1 1 - + + - - + - + = - + - +é ùë û + + + + + + + + + + mn a b mn m n m n m n m n m n m n d i c m m n n c dt c m n c n m m c m c n c n (16) Trong thực tế phương trình (16) bao gồm vô số phương trình, việc giải hệ phương trình này gặp rất nhiều khó khăn. Tuy nhiên, giả sử rằng tất cả các tương tác được xem xét ở đây là yếu , ,= a b , hệ lượng tử có thể được xem xét như kéo lượng tử phi tuyến. Và theo đó, tiến triển theo thời gian của hệ sẽ được giới hạn trong bốn trạng thái cộng hưởng 0 0 a b , 1 0 a b , 0 1 a b , 1 1 a b . Kết quả thu được là hệ phương trình (16) sẽ được giới hạn xuống hệ bốn phương trình cho biện độ xác suất tương ứng với , 0, 1=m n . Nghĩa là các biên độ xác suất , 0 khi , 0, 1= ¹m nc t m n , từ đó ta có thể viết lại hàm sóng dưới dạng “cắt” như sau: 00 01 10 11 0 0 0 1 1 0 1 1= + + + a b a b a b a bcut t c c c c (17) Với giả thuyết tại thời điểm ban đầu, hệ trong trạng thái chân không (0) 0 0 .= Từ đó ta thu được hệ bốn phương trình đơn giản sau: Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 77 * * * *00 01 10 01 10 11 00 *10 11 01 00 11 01 10 , , , . = + = + + = + + = + dc dc i c c i c c c dt dt dc dc i c c c i c c dt dt (18) Giải hệ phương trình trên trong trường hợp = với các điều kiện ban đầu: 00 11 10 010 0 0 0, 0 1= = = =c c c c ta thu được nghiệm tương ứng với một số trường hợp cụ thể: Trường hợp: = 2 00 11( ) ( ) 2i sin 2 -æ ö = = - ç ÷ è ø i tt c t c t e (19) 2 01 1 1 ( ) cos sin 2 2 2 2 -é ùæ ö æ ö = + -ç ÷ ç ÷ê ú è ø è øë û i t i t t tc t e i e (20) 2 10 1 1 ( ) cos sin 2 2 2 2 -é ùæ ö æ ö = - + -ç ÷ ç ÷ê ú è ø è øë û i t i t t tc t e i e (21) trong đó: 2 216= + . Tính Concurent theo công thức 00 11 01 102= -C c c c c và tính độ đan rối theo (7): 2 2 2 2 2 2 1 1 1 1 1 1 1 1 log 1 log 1 2 2 2 2 æ ö æ ö+ - + - + - + - = - - - -ç ÷ ç ÷ ç ÷ ç ÷ è ø è ø C C C C E t (22) Kết quả thu được thể hiện trên đồ thị tiến triển theo thời gian của độ đan rối các trạng thái được tạo ra (các dấu chấm) và các trạng thái được cắt ngắn theo mong muốn (đường liền nét) bởi bộ ghép bơm 2 mode như sau: Hình 3. Tiến triển độ đan rối của các trạng thái t được tạo ra (các dấu chấm) và các trạng thái được cắt ngắn theo mong muốn cut t (đường liền nét) bởi bộ ghép bơm 2 mode ;= = = 810 200 Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 78 Trường hợp: = - 2 00 11( ) ( ) 2i sin 2 æ ö = - = ç ÷ è ø i tt c t c t e (23) 2 01 1 1 ( ) cos sin 2 2 2 2 - é ùæ ö æ ö= + +ç ÷ ç ÷ê ú è ø è øë û i t i t t tc t e i e (24) 2 10 1 1 ( ) cos sin 2 2 2 2 - é ùæ ö æ ö= - + -ç ÷ ç ÷ê ú è ø è øë û i t i t t tc t e i e (25) Kết quả thu được thể hiện trên đồ thị tiến triển theo thời gian của độ đan rối của các trạng thái được tạo ra (đường chấm) và các trạng thái được cắt ngắn theo mong muốn (đường liền nét) bởi bộ ghép bơm 2 mode như sau: Hình 4. Tiến triển độ đan rối của các trạng thái t được tạo ra (đường chấm) và các trạng thái được cắt ngắn theo mong muốn cut t (đường liền nét) bởi bộ ghép bơm 2 mode ;= - = - = 810 200 Rõ ràng trong cả hai trường hợp trên hình 3 và hình 4 thì độ đan rối giải tích thu được rất phù hợp với kết quả tính số. Ta cũng nhận thấy đồ thị Tiến triển của độ đan rối của các trạng thái được tạo ra ở hai trường hợp trên hình 3 và hình 4 là như nhau. Điều này được giải thích đơn giản từ công thức tính concurent và công thức tính độ đan rối (22) trong hai trường hợp này là như nhau. Độ đan rối của trạng thái thu được có thể xấp xỉ hoặc thậm chí bằng 1, tuy nhiên cũng có những thời điểm trạng thái đan rối của hệ hoàn toàn bị biến mất (độ đan rối bằng không) rồi lại được tái sinh. Để đánh giá chất lượng của trạng thái quang học được cắt ngắn, bây giờ ta sẽ xét đến độ sai lệch giữa trạng thái hai qubit lý tưởng ˆ =cut cut cutt t và trạng thái đầu ra thực tế ˆ =t t t , trong đó, t được tính toán số dạng [11,15]. ˆexp( ) 01= -t iHt trong không gian Hilbert hai mode thực tế là vô hạn chiều. Trong phần tính toán số tôi sẽ đưa ra ở phụ lục, tôi chọn Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 79 số chiều là 20 trong mỗi không gian con. Độ chính xác của trạng thái cắt ngắn được tạo ra của phép cắt ngắn bằng kéo lượng tử ở trên được xác định bởi [11,15]: 2 1/2 ˆ ˆ ˆ ˆ ˆ, é ù= ê úë û cut cut cutF Tr (26) độ tin cậy được đo bằng ebit. Trong phần này, tôi tập trung vào trường hợp các trạng thái thuần được cắt ngắn. Khi đó độ chính xác ở (26) được đơn giản hóa thành: 2 = cut F t t (27) Độ chính xác của việc cắt ngắn lý tưởng bằng 1. Kết quả thu được từ việc tính số độ chính xác của sự cắt ngắn trong các trường hợp được thể hiện rõ trong hình 5 và hình 6. Hình 5. Độ chính xác giữa trạng thái thực được tạo ra t và trạng thái cắt ngắn lý tưởng cut t bởi bộ ghép bơm 2 mode ;= = = 810 200 10 Hình 6. Độ chính xác giữa trạng thái thực được tạo ra t và trạng thái cắt ngắn lý tưởng cut t bới bộ ghép bơm 2 mode ;= - = - = 810 200 10 Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 80 Kết quả thu được trên hình 5 và hình 6 cho thấy độ tin cậy của quá trình cắt trong trường hợp = đạt được là cao hơn so với trường hợp = - . Theo định nghĩa của fidelity (độ chính xác hay độ tin cậy của phép “cắt”), fidelity sẽ bằng 1 cho trường hợp chúng ta có phép “cắt” hoàn hảo. Với việc lấy số chiều của mỗi không gian Hilbert con là m=n=20, kết quả tính toán số độ tin cậy của trạng thái ( ) cut t và trạng thái thực ( )t được chúng tôi tính toán và thể hiện trên hình 5 và 6, với một số giá trị khác nhau của tham số đầu vào. Ta nhận thấy độ chính xác của việc cắt ngắn luôn xấp xỉ 1 trong một thời gian ngắn. Các giá trị của độ chính xác chỉ lệch khỏi 1 cỡ 43.10- , thậm chí là 42.10- , điều này chỉ ra sự phù hợp trong phương pháp phân tích để chỉ ra một thiết bị kéo lượng tử dùng để cắt ngắn các trạng thái tạo ra được trạng thái hai qubit có độ đan rối cao nhất trong thời gian tiến triển tương đối ngắn. Vào năm 2006, nhóm tác giả Miranowicz A. and Leoński W. cũng đã công bố công trình tính toán độ đan rối của trạng thái được tạo ra cũng như độ tin cậy của phép cắt ngắn này với các tham số đầu vào khác nhau và cũng thu được các kết quả tương tự. 3. KẾT LUẬN Bài báo giới thiệu tổng quan về trạng thái đan rối lượng tử, phân tích tính toán độ đan rối theo hai cách khác nhau. Chúng tôi cũng đưa ra các mô hình kéo lượng tử tuyến tính và kéo lượng tử phi tuyến và tập trung nghiên cứu mô hình kéo lượng tử phi tuyến có các mode tương tác tuyến tính được bơm 2 mode tạo ra không gian Hilbert hữu hạn chiều trong trường hợp không có mất mát và thu được những trạng thái có độ đan rối cao. Qua nghiên cứu, khảo sát chúng tôi đã thu được các trạng thái lượng tử hai qubit có độ đan rối xấp xỉ hoặc thậm chí bằng 1 từ việc sử dụng kéo lượng tử phi tuyến để cắt các trạng thái trong không gian Hilbert vô hạn chiều. Chất lượng của trạng thái tạo ra tương đối cao và được chúng tôi đánh giá qua đồ thị của độ chính xác giữa trạng thái thực được tạo ra và trạng thái lý tưởng theo mong muốn. Độ chính xác này xấp xỉ 1 và chỉ sai lệch cỡ 2.10-4. Các kết quả tính toán được so sánh giữa phương pháp tính số và phương pháp giải tích đã xác nhận giá trị của phương pháp giải tích mà chúng tôi đưa ra. Điều có thể được áp dụng như là nguồn nguyên liệu của giao thức viễn tải lượng tử và máy tính lượng tử trong tương lai không xa. TÀI LIỆU THAM KHẢO [1] Nguyễn Văn Hóa, Nguyễn Mạnh An, Cao Long Vân (2014), Ở ngưỡng cửa của cách mạng lượng tử trong tin học, Tạp chí Khoa học Trường Đại học Hồng Đức, số 19. [2] Cao Long Vân, Tạ Phương Hạnh (2005), Tin học lượng tử và máy tính lượng tử (I), Tạp chí ứng dụng toán học tập III, (số 1), trang 83-102. [3] Cao Long Vân (2005), Tin học lượng tử và máy tính lượng tử (II), Tạp chí ứng dụng toán học, tập III, (số 2), trang 77-100. Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping TẠP CHÍ KHOA HỌC TRƯỜNG ĐẠI HỌC HỒNG ĐỨC - SỐ 39.2018 81 [4] Cao Long Vân (2006), Tin học lượng tử và máy tính lượng tử (III): Các thuật toán lượng tử, Tạp chí ứng dụng toán học, tập IV, (số 1), trang 73-90. [5] Babichev S. A., Ries J. and Lvovsky A. I. (2003), Europhys. Lett. 64 1. [6] Gree Jaeger (2009), Entanglement, information and the interpretation of quantum mechanics, The Frontiers Collection, 50-52. [7] Kuang L.M., Wang F.B. and Zhou Y.G. (1993), Phys. Lett. A 183, 1. [8] Kuang L.M., Wang F.B. and Zhou Y.G. (1994), J. Mod.opt. 41, 1607 [9] Leonski W, Miranowicz A (2004), Kerr nonlinear coupler and entanglement, J.Opt. B: Quantum Semiclass. Opt, 6, pp 37-42. [10] Miranowicz A., Leonski W., and Imoto (2001), Quantum-Optical State in Finite- Dimensional Hilbert Space, J. Mod.opt. 155, 193. [11] Miranowicz A. and Leoński W. (2006), Two-mode optical state truncation and generation of maximally entangled states in pumped nonlinear couplers, J.Phys. B: At. Mol.Opt. Phys. 39. [12] Ozdemir S.K., Miranowicz A., Koasi M. and Imoto N (2001), Phys.Rev. A 64 063818. [13] Pegg D.T. and Barnett S.M. (1989), Phase properties of the quantized single-mode electromagnetic field, Phys.Rev.A. 39 1665. [14] Pegg D.T., Philips L.S. and Barnett S.M. (1998), Optical State Truncation by Projection Synthesis, Phys. Rev. Lett. 81 1604. [15] Wootters W.K. (1998), Entanglemen of Formation of an Arbitrary State of Two Qubits, Phys. Rev. Lett. 26, 78. ENTANGLEMENT STATES IN THE KERR - LIKE NONLINEAR COUPLER PUMPED ON TWO MODES Nguyen Thi Hong ABSTRACT In this paper, we study the Kerr - like nonlinear coupler consisting of two nonlinear oscillators that are linearly coupled together and affected by an external electromagnetic field being assumed to be in the form of continuous pulses in both modes. We explore that it is possible to apply the formalism of nonlinear quantum scissors to the system so that the system can be considered as a two-qubit system. By using transformational formulas for operators, we conduct modeling the quantum system, find out the analytical expressions of the probability amplitudes of time-dependent states, and thus generating maximal entangled states with high efficiency. Keywords: Entanglement state, quantum entanglement, von Neumann entropy, concurrence, quantum gates. Edited with the trial version of Foxit Advanced PDF Editor To remove this notice, visit: www.foxitsoftware.com/shopping
File đính kèm:
 cac_trang_thai_dan_roi_trong_bo_ghep_phi_tuyen_kieu_kerr_duo.pdf
cac_trang_thai_dan_roi_trong_bo_ghep_phi_tuyen_kieu_kerr_duo.pdf

