Bài giảng Vật lý đại cương A2 - Chương 4: Thuyết tương đối hẹp

 CHƯƠNG IV
THUYẾT TƯƠNG ĐỐI HẸP
Cơ học Newton (cơ học cổ điển) ra đời từ nữa 
cuối thế kỷ XVII đóng vai trò hết sức to lớn. 
Trong cơ học Newton người ta quan niệm không 
gian có tính tuyệt đối và được mô tả bằng hình 
học Euclide. Thời gian cũng có tính tuyệt đối.
 Cuối thế kỷ 19 và đầu thế kỷ 20, khi nghiên cứu 
đến những hiện tượng liên quan đến ánh sáng 
hoặc những vận tốc lớn so sánh được với vận 
tốc ánh sáng, người ta nhận thấy rằng những 
khái niệm cũ không còn phù hợp nữa. Trong 
tình hình đó, thuyết tương đối ra đời xây dựng 
lại những khái niệm không gian và thời gian 
khác hẳn với những khái niệm của Newton.
TTĐ Einstein gồm hai phần:
+ TTĐ hẹp ra đời 1905 nghiên cứu các HQC 
quán tính.
+ TTĐ rộng ra đời 1916 nghiên cứu các HQC 
không quán tính.
Trong phần này chúng ta chỉ nghiên cứu thuyết 
tương đối hẹp.
I. Nguyên lý Galilê, phép biến đổi Galilê
Giả sử ta có hệ K’ chuyển động đối với hệ K với 
vận tốc v không đổi dọc theo trục x và lúc đầu 
gốc hai tọa độ trùng nhau. Khi đó ta có hệ thức:
  y y’
r r'''' OO r vt M
 K K’
Chiếu hệ thức trên xuống 
 các trục tọa độ ta được: r r '
 x x'' vt
 O O’
 y y ' x x’
 z z’
 z z '
 Các hệ thức này gọi là phép biến 
 t t ' đổi Galilée 
 Phép biến đổi Gallilée dẫn đến một số KQ sau:
 2 2 2
a) Gọi l ()()() x1 x 2 y 1 y 2 z 1 z 2
 là khoảng cách giữa hai điểm 1, 2 trong hệ K; 
 khoảng cách tương ứng trong hệ K’ là:
 2 2 2
 l'('')('')('') x1 x 2 y 1 y 2 z 1 z 2
 Ta có : l ' l : khoảng cách giữa hai điểm
 là đại lượng bất biến .
 Lấy đạo hàm các hệ thức trên theo thời gian
 ux u';';' x v u y u y u z u z
 Các hệ thức này là phép cộng vận tốc cổ điển.
 Từ nhiều quan sát và thí nghiệm, cơ học Newton 
 rút ra nhận xét sau đây gọi là nguyên lý Galilée:
 Các định luật cơ học đều như nhau trong các hệ 
 qui chiếu quán tính.
2. Về quang học ta đã biết lí thuyết hạt ánh sáng 
 của Newton và lí thuyết sóng AS của Huygens. 
 Lúc đầu thuyết sóng không được chú ý . Mãi đến 
 đầu thế kỷ XIX nó mới được thừa nhận một cách 
 rộng rãi. Nhưng quan niệm AS có tính chất sóng 
 thì đồng thời cũng phải quan niệm trong thiên 
 nhiên tồn tại môi trường vật chất đặc biệt để lan 
 truyền sóng AS. Người ta gọi môi trường đó là ête 
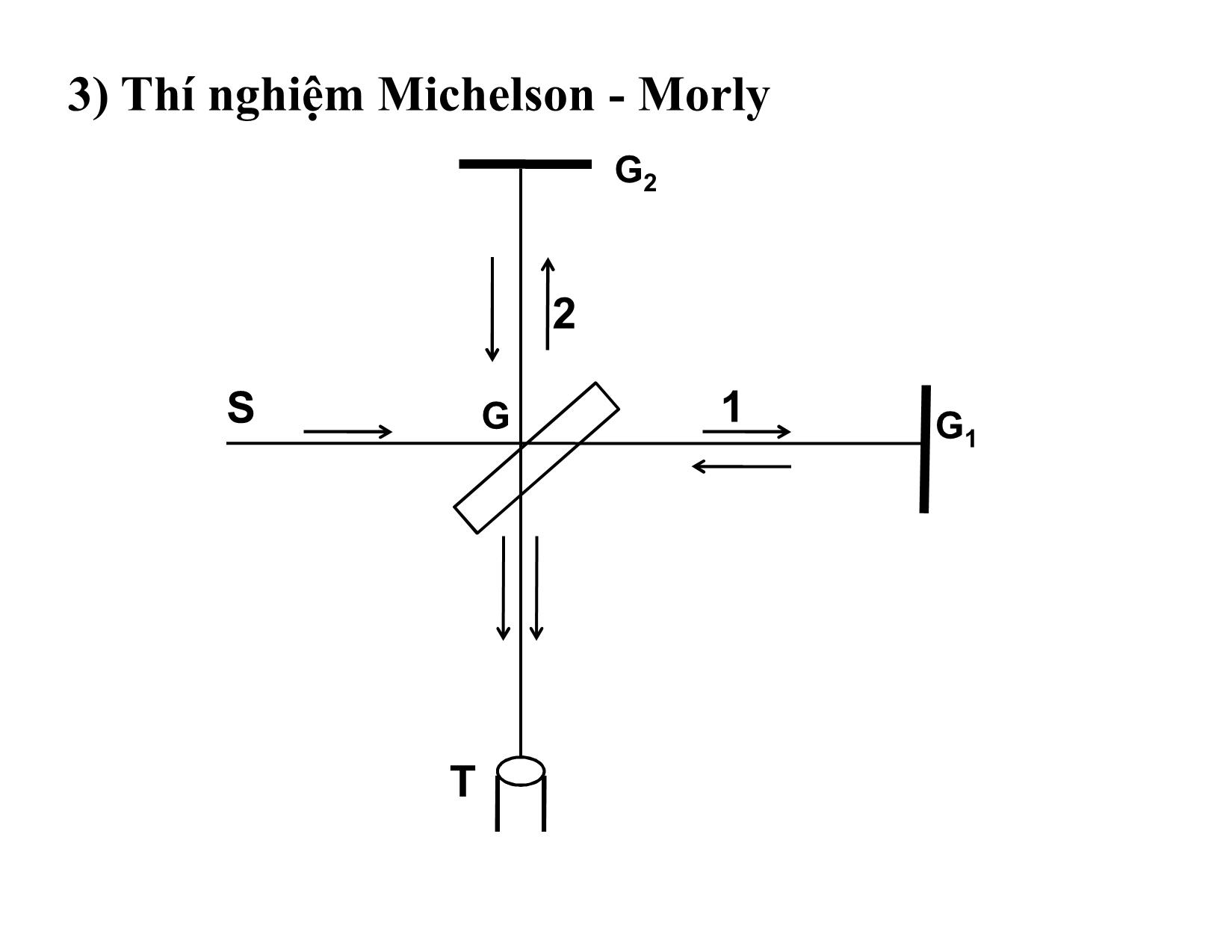
3) Thí nghiệm Michelson - Morly
 G2
 2
 S G 1
 G1
 T
Một tia sáng đơn sắc từ nguồn S đến gương nữa 
phản xạ G, một phần phản xạ (2) và phần truyền 
qua (1). Tia (2) đến gặp gương G2 sau đó lại quay 
về G. Còn tia (1) sau khi gặp G1 cũng trở về G. 
Các tia này cuối cùng cũng rơi vào giao thoa kế T 
Giả sử thiết bị này được đặt sao cho gương GG1
song song còn phương GG2 vuông góc với 
phương chuyển động của Trái đất (trong ête).
Gọi v là vận tốc chuyển động của Trái đất còn c là 
vận tốc ánh sáng trong ête, GG1 = GG2 = l . 
• Thời gian ánh sáng đi trên đoạn đường GG1 G:
 l l2 l 1
 t (1)
 1 c v c v c v2
 1 
 c2
• Thời gian ánh sáng đi trên đoạn đường GG2 G:
 2l 2 l 1
 t2 (2)
 c2 v 2c v 2
 1 
 c2
Vận tốc Trái đất chung quanh Mặt Trời cũng là 
vận tốc của nó trong ête (vận tốc tuyệt đối của 
 v2
Trái Đất) thì v = 30km/s và 10 8 do đó:
 c2
 2
 2l v 2 l2 v
 t1 1 2 1  ;  
 c c c c
 2
 2l v 2 l 1 2 
 t2 1 2 1  
 c 2 c c 2 
• Hiệu quang lộ của hai tia đó là:
 2
 1 L 1 L 2 c() t 1 t 2 l 
• Bây giờ quay giao thoa kế một góc 900 sao cho 
 G2 G trùng còn G1 G vuông góc với phương 
 chuyển động của Trái Đất. Hiệu quang lộ của hai 
 tia sẽ là 
 2
 2 l 
 G2
S G
 G1
• Vậy hiệu quang lộ đã thay đổi một lượng là:
 2
 2  1 2l 
• Hệ thống vân sẽ dịch chuyển đi một đoạn là:
 2l 2
 m khoảng vân
 
 Trong thí nghiệm Michelson l = 11m; λ = 0,59µm, 
 ta suy ra m = 0,37 khoảng vân. Tuy nhiên làm TN 
 nhiều lần trong suốt thời gian một năm rưỡi, 
 Michelson không phát hiện được độ dịch chuyển 
 đó. Điều này hoàn toàn mâu thuẩn với giả thiết 
 tồn tại ête.
II. Các tiên đề của Thuyết Tương Đối Hẹp
 Để lí giải những mâu thuẩn trên Einstein đã nêu 
 lên hai tiên đề sau đây:
1. Mọi định luật vật lý đều như nhau trong các 
 hệ qui chiếu quán tính.
 2.Vận tốc ánh sáng trong chân không đều 
 bằng nhau đối với mọi hệ qui chiếu quán 
 tính và không phụ thuộc chuyển động của 
 nguồn sáng.
III. Phép biến đổi Lorentz
 Giả sử có hai HQC K và K’, K’chuyển động đối 
 với vận tốc v không đổi như hình vẽ. Giả sử lúc 
 ban đầu O và O’ trùng nhau. Gọi xyzt và x’y’z’t’ 
 là các tọa độ không gian và thời gian trong các hệ 
 K và K’. y
 y’
 ’ x’
 O O x’
 x x
 z z’
Các công thức của phép biến đổi Galile không thể 
dùng để xác định quan hệ giữa các tọa độ trên vì 
chúng mâu thuẩn với tiên đề thứ hai của Einstein
Để tìm các công thức biến đổi tọa độ không gian 
và thời gian từ hệ này sang hệ kia ta viết các công 
thức biến đổi dưới dạng sau:
 x’ = f1 (x, y, z, t) ; y’ = f2 (x, y, z, t) 
 z’ = f3 (x, y, z, t) ; t’ = f4 (x, y, z, t) 
Từ tính đồng nhất của KG và thời gian ta suy ra 
các phép biến đổi trên phải là tuyến tính.
Vì hệ K’ chuyển động dọc  ... 
trục x nên: y’ = y ; z’ = z
Vì các tọa độ y và z biến đổi độc lập với x và t nên 
các tọa độ x và t cũng biến đổi độc lập với y và z. 
Trong các công thức biến đổi của x và t không có 
mặt y và z. Như vậy x và t có thể là các hàm 
tuyến tính chỉ của x’ và t’.
Gốc tọa độ O’ của hệ K’ có tọa độ x’ = 0 trong hệ 
K’ và x = Vt trong hệ K. Do đó biểu thức x – Vt 
phải triệt tiêu đồng thời với tọa độ x’. Muốn vậy 
phép biến đổi tuyến tính phải có dạng: 
 x'  ( x vt ) (1)
Tương tự, gốc tọa độ O của hệ K có tọa độ x = O 
trong hệ K và x’ = -Vt’ trong hệ K’. Từ đó suy ra: 
 x  ( x ' vt ') (2)
Ta sẽ sử dụng các tiên đề Einstein để xác định hệ 
số  . Giả sử tại thời điểm t = t’ = 0 ta làm lóe lên 
một chớp sáng ở gốc chung của K và K’. Trong 
hai hệ K và K’ ta có :
 x = ct ; x’ = ct’ 
Nhân (1) với (2)
 x.''' x  2 x vt x vt 
  2(xx ' xvt ' vtx ' vtt 2 ')
  2(xx ' ctvt ' vtct ' vtt 2 ')
 c2 tt'()'  2 c 2 v 2 tt
 2
 2 2 2 2 2 c
 c  c v  2 2
 c v
 1
  
 v2
 1 
 c2
Thay vào (1) và (2) ta được:
 x vt x'' vt
 x' (3) ; x (4)
 v2 v 2
 1 1 
 c2 c 2
Từ (3) và (4) ta tính được:
 v v
 t 2 x t'' 2 x
 t'; c t c
 v2 v 2
 1 1 
 c2 c 2
• Các công thức biến đổi Lorentz 
 Từ K K’ 
 x vt
 x';'; y y
 v 2
 1 
 c 2
 v
 t 2 x
 z';' z t c
 v 2
 1 
 c 2
• Từ K’ K
 x'' vt
 x ;' y y
 v 2
 1 
 c 2
 v
 t'' 2 x
 z z'; t c
 v 2
 1 
 c 2
Ý nghĩa của các công thức biến đổi Lorentz
Từ các công thức biến đổi Lorentz ta thấy:
+ Khi v << c, các phép biến đổi Lorentz trở về 
các biến đổi Galilée. 
+ Khi v c các công thức biến đổi Lorentz mất ý 
nghĩa. Điều đó có nghĩa là theo lí thuyết Einstein 
thì vận tốc AS trong chân không là vận tốc giới 
hạn. Vận tốc truyền trong không gian của bất kỳ 
quá trình vật lý thực nào cũng không thể lớn hơn 
hay bằng c.
+ KG và thời gian có tính tương đối gắn liền với 
nhau và gắn liền với vật chất chuyển động. 
III. Các hệ quả của phép biến đổi Lorentz.
1.Tính tương đối của sự đồng thời – Quan hệ nhân 
 quả.
 Giả sử trong hệ K có hai biến cố A(x1,t1) và 
 B(x2,t2) xảy ra. Khoảng thời gian giữa hai biến cố 
 đó trong hệ K’ là:
 v
 t t x x 
 2 1c2 2 1
 t''' t2 t 1 
 v2
 1 
 c2
Vậy nếu hai biến cố xảy ra đồng thời trong hệ K 
(t1=t2) sẽ không đồng thời trong hệ K’(trừ trường 
hợp x1=x2). Vậy sự đồng thời có tính tương đối.
Công thức trên cũng chứng tỏ rằng đối với các 
biến cố đồng thời trong hệ K, dấu của t’2 – t’1
được xác định bởi dấu của biểu thức (x2 – x1 )V. 
Do đó trong các hệ quán tính khác nhau ( với các 
giá trị khác nhau của V), hiệu t’2 – t’1 sẽ không 
những khác nhau về độ lớn mà còn khác nhau về 
dấu. Điều này có nghĩa là thứ tự xảy ra của các 
biến cố A và B có thể bất kỳ.
• Quan hệ nhân quả: Giả sử biến cố A là một phát 
 súng nổ tại một điểm có tọa độ (x1 , y1 , z1 ) vào 
 thời điểm t1 và biến cố B là viên đạn trúng đích 
 tại điểm có tọa độ (x2 , y2 , z2 ) vào thời điểm t2 . 
 Đó là hai biến cố có quan hệ nhân quả: A là 
 nguyên nhân, B là kết quả. Coi hai biến cố đều 
 xảy ra trên trục x. Trong hệ K t2 > t1 .Gọi u là vận 
 tốc trung bình của viên đạn và giả sử x2 > x1 . Ta 
 có:
 x x
 u 2 1
 t2 t 1
Trong hệ K’ hai biến cố này xảy ra tại thời 
điểm t’1 và t’2 với: 
 t t v
 t' t' 2 1 1 u 
 2 1 2 
 v2 c
 1 
 c2 
Ta luôn có u t1 thì t’2 > 
t’1. Nghĩa là trong cả hai hệ K và K’ thứ tự 
nhân quả bao giờ cũng được tôn trọng. 
2.Sự co ngắn Lorentz
 Giả sử có một thanh nằm yên trong hệ K’ dọc 
 theo trục x’. Gọi x’1 và x’2 là tọa độ hai đầu 
 thanh, lo là chiều dài của thanh trong hệ K’, ta 
 có: lo = x’2 – x’1
 Muốn xác định chiều dài của thanh trong hệ K ta 
 phải xác định tọa độ hai đầu thanh trong hệ K tại 
 cùng thời điểm. Theo biến đổi Lorentz ta có:
 v v
 x t x t
 2c2 2 1 c 2 1
 x''2 x 1 
 v2 v 2
 1 1 
 c2 c 2
Vì t1 = t2 nên:
 x2 x 1 l
 x''2 x 1 lo 
 v2 v 2
 1 1 
 c2 c 2
 v2
 l l 1 
 o c2
Do đó l < lo. Vậy khi vật chuyển động kích thước 
của nó bị co ngắn theo phương chuyển động.
 Chiều dài của thanh đo được trong hệ qui chiếu 
mà thanh đứng yên gọi là chiều dài riêng.
3.Sự chậm trễ của đồng hồ chuyển động.
 Tại một điểm cố định A’ trong hệ K’ xảy ra hai 
 biến cố 1 và 2. Chẳng hạn biến cố 1 là kim của 
 đồng hồ đặt tại A’, chỉ thời điểm t’1 , còn biến cố 
 2 là kim của cùng đồng hồ ấy chỉ thời điểm t’2 
 Khoảng thời gian giữa hai biến cố trong hệ K’ là
 t0 t'' 2 t 1 được gọi là thời gian riêng của K’
 Bây giờ giả sử ta muốn đo khoảng thời gian giữa 
 hai biến cố này trong hệ K. Rõ ràng không thể so 
 sánh các số chỉ của đồng hồ A’ với số chỉ một 
 đồng hồ nào đó trong hệ K. Vì vậy ta phải tiến 
 hành phép đo như sau.
Giả sử đồng hồ A’ có tọa độ x’. Vào lúc t’1 nó 
trùng với một đồng hồ nào đó của hệ K và đồng 
hồ này chỉ t1 . Sau đó đến lúc đồng hồ A’ chỉ t’2 nó 
lại trùng với một đồng hồ khác của hệ K và đồng 
hồ này chỉ t2 . Theo các phép biến đổi Lorentz
 v v
 t''''2 2 x t 1 2 x
 c c t0
 t t2 t 1 
 v2 v 2 v 2
 1 1 1 
 c2 c 2 c 2
 t t0
 t chính là khoảng thời gian giữa hai biến cố 1 
và 2 đo được từ hệ K. Vì t t 0 nên đồng hồ 
chuyển động chạy chậm hơn đồng hồ đứng yên.
Giả sử một hạt chuyển động với vận tốc v theo 
chiều dương của trục x trong hệ qui chiếu quán 
tính K. Thời gian ghi được trên đồng hồ gắn liền 
với hạt gọi là thời gian riêng τ của hạt. Vậy 
khoảng thời gian ∆τ của quá trình xảy ra trên hạt 
và khoảng thời gian ∆t của quá trình đó trong hệ 
K liên hệ như sau
 
 t 
 1 v2 / c 2
4. Khoảng giữa hai biến cố:
 Xét hai biến cố A và B. Khoảng cách không gian 
 của chúng trong hệ K là:
 2 2 2 2 2 2
 (xBABABA x ) (y y ) (z z ) x y z
 Khoảng cách thời gian của chúng là:tBA t t
 Trong thuyết tương đối , khoảng giữa hai biến cố 
 là đại lượng định nghĩa:
 s c2 t 2 () x 2 y 2 z 2
 Trong hệ K’, khoảng giữa 2 biến cố trên bằng:
 s''(''') c2 t 2 x 2 y 2 z 2
 Theo phép biến đổi Lorentz, ta có:
 v
 t x
 x v t 2
 x';';';' y y z z t c
 v2 v 2
 1 1 
 c2 c 2
 Do đó ∆S = ∆S’ nên khoảng là đại lượng bất biến.
 Vậy các đại lượng bất biến của thuyết tương đối 
 là: vận tốc ánh sáng c, thời gian riêng, độ dài 
 riêng, khoảng
5. Hiệu ứng Doppler cho ánh sáng:
 Là hiện tượng ánh sáng đổi màu khi nguồn sáng 
 chuyển động so với người quan sát.
 Giả sử một nguồn sáng đang chuyển động theo 
 phương x và phát ra hai tia sáng tại hai vị trí x1
 và x2 cách người quan sát trên mặt đất các 
 khoảng r1 và r2 . Trong hệ qui chiếu của nguồn 
 sáng thì khoảng thời gian giữa hai lần tia sáng 
 phát ra là Δτ. Khoảng thời gian trên mặt đất là:
 t t2 t 1  
Khoảng Δt này không phải thời gian giữa hai lần 
người quan sát trên mặt đất nhìn thấy các tia 
sáng. Vì sau khi phát ra, các tia sáng phải vượt 
qua các khoảng cách r1 và r2 để tới được mắt 
người quan sát .
 x1 x2
 θ
 r2
 r1
 Cho nên khoảng thời gian giữa chúng sẽ là:
 Ttrctrc (/)(/)()/2 2 1 1 trrc 1 2
Trong các trường hợp thực tế thì nguồn sáng 
 thường ở rất xa nên :
 r1 r 2 ( x 1 x 2 )cos v t cos 
 T t v tcos / c t (1  cos  )
 (1  cos  )  ;  v / c
 Nếu nguồn sáng phát ra ánh sáng liên tục thì tần 
 số ánh sáng quan sát được trên mặt đất là:
 1 1 f
 f 0
 T (1  cos  )   (1  cos  )
 f0 1/  là tần số riêng trong hệ qui chiếu 
của nguồn sáng.
 Các trường hợp đặt biệt:
a)Nguồn sáng ở rất xa và đang tiến lại gần : θ = 00
 f 1 
 f 0 f
 (1  )0 1 
Như vậy các nguồn sáng đang tiến lại gần sẽ có 
màu xanh hơn, hiện tượng này được gọi là dịch 
chuyển xanh (blue - shifted)
b) Nguồn sáng ở rất xa đang ra xa: θ = 1800 
 f 1 
 f 0 f
 (1  )0 1 
 Các nguồn sáng đang chạy ra xa sẽ có màu đỏ 
 hơn, hiện tượng này gọi là dịch chuyển đỏ (red –
 shifted). Cho đến nay trong phạm vi quan sát 
 được người ta đều thấy các vì sao có dịch chuyển 
 đỏ nên giả thuyết vũ trụ đang giãn ra là có lý.
 0
c) Trường hợp θ = 90 : f = γf0 
Ví dụ:
1. Một hình tam giác vuông cân đứng
 yên trong hệ qui chiếu K, có diện tích
 bằng S. Tìm diện tích của tam giác này
 và các góc của nó trong hệ qui chiếu
 K’ chuyển động đối với hệ K với vận
 tốc bằng 4/5 c theo phương song song
 với cạnh huyền của tam giác.
• Gọi l0 và h0 là cạnh huyền và chiều cao của tam 
 giác trong hệ qui chiếu K. Ta có:
 1
 S l. h
 2 0 0
• Theo phép biến đổi Lorentz, chiều cao và cạnh 
 huyền của tam giác trong hệ qui chiếu K’ là:
 v2
 h h; l l 1 0,6 l
 0 0c2 0
 1 1
 S h. l 0,6. h . l 0,6 S
 2 2 0 0
 h2 h 2h
 tg 0
 l/ 2 l 0,6 l0
 2h 2
 0 tg450 1,67
 1,2l0 / 2 1,2
  590
Vậy 2 góc là 590 h
và một góc là 620
 l
2. Tìm độ dài riêng của một thanh, 
 nếu trong hệ qui chiếu phòng thí 
 nghiệm, vận tốc của nó là v = c/2, 
 độ dài là 1m và góc của nó và 
 phương chuyển động là  45o
• Độ dài riêng của thanh:
 2 2
 l0 l 0x l 0 y
• Theo phép biến đổi Lorentz
 2
 v lx
 lx l0 x1 2 l 0 x 
 c v2
 1 
 c2
 l cos
 ;l0 y l y l sin
 v2
 1 
 c2
Vậy:
 l 2cos 2 
 l' l2 sin 2  1,08 m
 v2
 1 
 c2
 l
 ly
 lx
3. Thời gian sống riêng của một hạt 
 không bền nào đó là  o 10 ns . Tìm 
 quãng đường hạt đi được trước khi 
 phân rã trong hệ qui chiếu phòng thí 
 nghiệm, trong đó thời gian sống của hạt 
 là t 20 ns
• Theo phép biến đổi Lorentz ta có:
 2
 0  0 
 t v c 1 
 v2  
 1 
 c2
 2
  0 
 s v c  1 
  
 3
 3.108 .20.10 9 . 5,2m
 2
VI. Phép biến đổi vận tốc
Gọi u ( u x , u y , u z ),'(',',') u u x u y u z là vận tốc 
chất điểm trong hệ K và K’
Theo định nghĩa vậndx' tốc ta có: dx
 u'
 x dt', u x dt
 v
 dt dx
 dx vdt 2
 dx';' dt c
 1 v2 / c 2 1 v 2 / c 2
 dx vdt u v
 u ' x
 x v v
 dt dx1 u
 c2 c 2 x
 v2 v 2
 uy1 2 u z 1 2
u';' c u c
 yv z v
 1 u 1 u
 c2x c 2 x
Trong phép biến đổi ngược lại từ K’ K . Ta được:
 v2
 u ' 1 
 u' v y 2
 u x ; u c
 xv y v
 1 u ' 1 u '
 c2x c 2 x
 v2
 u 'z 1 2
 ; u c
 z v
 1 u '
 c2 x
Ví dụ:
1. Hai hạt chuyển động với các vận tốc v1
 = 0,5 c và v2 = 0,75 c trong hệ qui chiếu
 phòng thí nghiệm. Tìm vận tốc tương
 đối của chúng khi:
 a) Hai hạt chuyển động đến gặp nhau
 b) Hai hạt chuyển động vuông góc với
 nhau
a) Chọn HQC K và K’ với trục x và x’ cùng phương 
 với phương chuyển động của hai hạt, chiều 
 dương là chiều chuyển động của hạt 1. Gắn HQC 
 K’ với hạt 2. Vậy vận tốc của hạt 1 đối với hạt 2 
 chính là vận tốc của hạt 1 trong HQC K’. Theo 
 công thức biến đổi vận tốc ta có:
 v2
 u 1 
 u v y 2
 u';' x u c
 xv y v
 1 u 1 u
 c2x c 2 x
Trong đó:
 ux = v1 = 0,5c ; v = -v2 = -0,75 c 
 uy = 0 1 2
 v v 1,25c
 u' 1 2 0,91 c
 x v
 1 2 v 1,375
 c2 1
 2 2
 u'y 0 u ' u ' x u ' y 0,91 c
b) Chọn HQC K và K’ với trục x và x’ cùng 
 phương chiều với hạt 2. Gắn HQC K’ với hạt 2. 
 Vậy vận tốc của hạt 1 đối với hạt 2 chính là vận 
 tốc của hạt 1 trong HQC K’. Theo công thức biến 
 đổi vận tốc ta có: v2
 u 1 
 u v y 2
 u';' x u c
 xv y v
 1 u 1 u
 c2x c 2 x
• Trong đó ux = 0 ; uy = v1 ; v = v2
• Vậy: 
 v2
 u' v ; u ' v 1 2
 x2 y 1 c2
 2 1
 2 2 2 2 v2 
 u' u 'x u ' y v2 v 1 1 2 
 c 2
 2
 2 2 v1 v 2 
 v2 v 1 
 c 
IV. Động lực học tương đối tính:
1. Khối lượng tương đối tính: theo cơ học cổ điển, 
 khối lượng của một vật là hằng số không phụ
 thuộc vật đứng yên hay chuyển động, tuy nhiên
 theo thuyết tương đối thì:
 m
 m o
 1 v2 / c 2
 m là khối lượng chất điểm trong hệ mà nó
 chuyển động với vận tốc v gọi là khối lượng
 tương đối, mo là khối lượng chất điểm đo được
 trong hệ mà nó đứng yên gọi là khối lượng nghĩ.
2. Động lượng tương đối tính:
  m 
 p mv o v
 1 v2 / c 2
3. Phương trình động lực học của chất điểm: 
  
  d p d d m v
 F () mv 0 
 dt dt dt v2 
 1 
 c2 
4. Năng lượng tương đối
 Theo ĐL bảo toàn năng lượng, độ tăng năng 
 lượng của vật bằng công của ngoại lực tác dụng 
 lên vật. Giả sử lực tác dụng và phương chuyển 
 động cùng hướng theo chiều dương của trục x.
 d
 dE dA dE Fdx () mv dx
 dt
 dx
 d()() mv mdv vdm v
 dt
 mo 2 2 2 2 2
Mà m m c m v mo c
 1 (v2 / c 2 )
Lấy vi phân hai vế:
2mc2 dm m 2 2 vdv v 2 2 mdm 0
 mvdv v2 dm c 2 dm () mdv vdm v c 2 dm
 dE c2 dm E mc 2 C
C là hằng số tích phân. Do điều kiện m = 0 
thì E = 0, nên E = 0. Vậy:
 E = mc2 
5.Hệ quả:
a) Năng lượng nghĩ của vật: 
 2
 Eo m o c
mo là khối lượng lúc vật đứng yên
b)Động năng tương đối
 2 2 2 1 
 T mc mo c m o c 1
 v2 
 1 
 c2 
c) Hệ thức liên hệ giữa năng lượng và động lượng 
 của vật 2 2
 2mo c 2 v 2 4
 E mc E 1 2 mo c
 v2 c 
 1 
 c2
Thay E =mc2 và p = mv vào biểu thức trên ta được:
 2 2 4 2 2 2 2 2 2 4
 E mco pc E pc mc o in var
Vậy : E2 p 2 c 2 là bất biến.
d) Từ
 m
 o
 m 
 v2
 1
 c2
Ta suy ra nếu vật có khối lượng nghĩ mo
 khác không thì phải chuyển động với 
 vận tốc nhỏ hơn c. Hạt photon chuyển 
 động với vận tốc bằng c nên khối lượng 
 nghĩ của nó bằng không.
Ví dụ:
1. Tìm vận tốc của một hạt để động
 lượng tương đối tính của nó lớn hơn
 n = 2 lần động lượng Newton của nó.
1. Tính công cần thực hiện để tăng vận
 tốc của một hạt có khối lượng nghĩ mo
 từ 0,6 c đến 0,8 c? So sánh kết quả thu
 được với giá trị được tính theo công
 thức cổ điển.
1. Động lượng TĐT và động lượng Newton
 m0 v
 p ; p0 m 0 v
 v2
 1 
 c2
 2
 m0 v v 1
 n. m0 v 1 2 2
 v2 c n
 1 
 c2
 c c 3
 v n2 1 
 n 2
2. Công tính theo cơ học tương đối tính và theo cổ 
 điển
 1 1 2
 A T2 T 1 m 0 c
 v2 v 2 
 1 2 1 1 
 c2 c 2 
 2
 0,42m0 c
 1 2 2 2
 A0 m 0 v 2 v 1 0,14 m 0 c
 2
3. Một hạt có khối lượng nghĩ mo , tại thời điểm t = 
 0 bắt đầu chuyển động dưới tác dụng của lực F 
 không đổi. 
 a) Tìm sự phụ thuộc theo thời gian t của vận tốc 
 của hạt và của quãng đường mà hạt đi được.
 b) Nếu hạt chuyển động dọc theo trục x theo 
 phương trình x A 2 c 2 , tìm lực tác dụng lên 
 hệ. 
3. 
 dp p t
 F dp Fdt p Ft
 dt 0 0
 m v Fct
 0 Ft v 
 v2 m 2 c 2 F 2 t 2
 1 0
 c2
 22 2
 ds m c 2 2 m c
 v s 0 c t 0
 dt F F
b)
 x A2 c 2 t 2
 dx c2 t m v m c2 t
 v p 0 0
 dtA2 c 2 v 2 A
 1 
 c2
 dp m c2
 F 0
 dt A
 235
4) Khi phân chia của một hạt nhân 92 U năng 
 lượng lượng giải phóng ra khoảng 200MeV . Tìm 
 độ thay đổi khối lượng khi phân chia 1 kmol 
 uran.
 Giải
 E
 E m. c2 m 
 c2
 200.1,6.10 13 .6,023.10 26
 0,214kg
 9.1016
6. Xuất phát từ phương trình cơ bản 
 động học tương đối tính, tìm:
 a) Trong những trường hợp nào gia 
 tốc của hạt trùng phương với lực F tác 
 dụng lên hạt
 b) Các hệ số tỉ lệ giữa lực F và gia tốc a 
 trong các trường hợp mà F thẳng góc v 
 và F song song v, trong đó v là vận tốc 
 hạt
• a)
 1
  
  d p d v2 2
 F ( m0 v ) ;  1 2 
 dt dt c 
 dv d
  m m v
 0dt 0 dt
 1 3
 d d v2 2 v 2 2 1 dv 2
 1 2 1 2 2
 dt dt c c 2 c dt
 dv2 d dv d  3 
 (v )2 2 v . 2 v . a ( v . a )
 dt dt dt dt c2
   3 
 F  m a m v(.) v a
 0 0 c2
 Vậy lực F chỉ song songvới gia tốc trong hai 
 trường hợp duy nhất là khi v  a và khi v a
b)   
 F v v  a F  m0 a
   v2 
 F v v  a F  m a  3 m a
 0 0 c2
  2 
 3 1 v 3
 F  m0 a 2 2  m 0 a
  c