Bài giảng Vật lý đại cương A2 - Chương 2: Dao động. Sóng
Nói một cách khác :
Sóng truyền theo một phương xác định và đặc
trưng bằng các dao động xảy ra hoàn toàn giống
nhau trên các mặt phẳng thẳng góc với phương
truyền sóng được gọi là sóng phẳng chạy . Biểu
thức trên mô tả sóng phẳng chạy theo trục y với
vận tốc v gọi là hàm sóng.
Sóng phẳng đơn sắc là sóng mà dao động tại mỗi
điểm là dao động điều hoà
u(y,t) u(0,t ') hay u(y,t) f (t y)
Xét một sóng phẳng truyền theo phương Oy
trùng với tia sóng. Giả sử dao động của phần tử
nằm tại điểm O ứng với tọa độ y = 0 có dạng
Hàm sóng tại M:
u A.cost

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
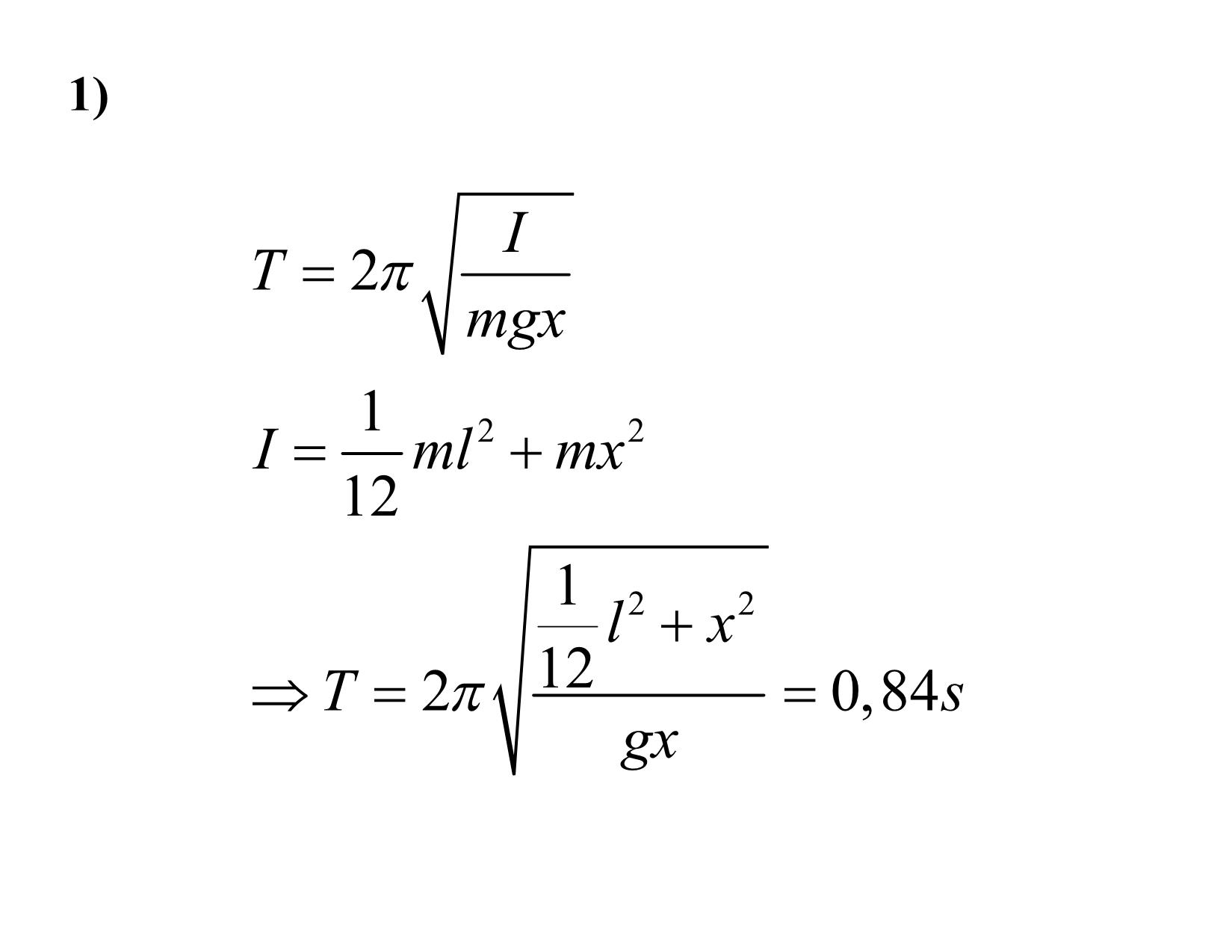
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Vật lý đại cương A2 - Chương 2: Dao động. Sóng", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Vật lý đại cương A2 - Chương 2: Dao động. Sóng

CHƯƠNG II DAO ĐỘNG -SÓNG A. DAO ĐỘNG I. Dao động cơ điều hòa L O x 1. DĐĐH của con lắc lò xo: M x x F m a k x d 2 x d 2 x m k x 2 x 0 d t 2 d t 2 o k 0 m Nghiệm của nó là: x A 0 c o s 0 t A0 , là các hằng số phụ thuộc các điều kiện ban đầu. Chu kỳ dao động: 2 m T 2 0 k 0 • Vận tốc và gia tốc của CLLX DĐ ĐH: v x' A00 sin(0t ) 2 2 a v' x '' A00 cos(0t ) 0 x vmax A00 2 amax 0 A0 2 2 2 2 v 0 (A0 x ) • Năng lượng DĐĐH: W = Wđ + Wt mv2 1 W m 2 A2 sin2 t d 2 2 0 0 0 • Nếu qui ước thế năng tại vị trí cân bằng bằng 0 thì: 0 1 1 W kxdx kx2 kA2 cos2 ( t ) t 0 0 x 2 2 1 • Vậy: W k A 2 : Cơ năng được bảo toàn 2 0 2. Con lắc vật lý Con lắc vật lý là một vật rắn khối lượng m, có thể quay xung quanh một trục cố định nằm 0 ngang. 2 d G M I P.OG I t dt 2 P mg sin mg t 0’ 2 2 mgl d d 2 + 0 mgl I o 0 I dt 2 dt 2 I là momen quán tính của vật rắn đối với trục quay, l = OG là khoảng cách từ trục quay đến trọng tâm G của vật rắn Vậy khi góc α nhỏ con lắc vật lý dao động điều hoà với chu kỳ 2 I T 2 o mgl Đối với con lắc đơn thì : I = ml2 nên : mgl mgl g 0 I ml 2 l l T 2 g Ví dụ: 1) Xác định chu kỳ của con lắc vật lý, được cấu tạo bằng một thanh đồng chất chiều dài L = 30cm. Điểm treo của con lắc cách trọng tâm một khoảng x = 30cm. 1) I T 2 mgx 1 I ml 2 mx2 12 1 l 2 x2 T 2 12 0,84s gx 2) Một thanh đồng chất có độ dài l thực hiện dao động nhỏ xung quanh một trục nằm ngang OO’, vuông góc với thanh và đi qua một trong các điểm của nó. Tìm khoảng cách giữa tâm quán tính của thanh và trục OO’, khi chu kỳ dao động là nhỏ nhất. Chu kỳ đó bằng bao nhiêu? 2) I 1 T 2 ; I ml 2 mx2 mgx 12 1 2 2 l x 2 2 l 12x T 2 12 2 gx 12gx 2 2 T khi: d l 12x l min 0 x dx 12gx 2 3 l T 2 min g 3 Bài tập: 1) Một con lắc vật lý thực hiện dao động bé xung quanh một trục nằm ngang với tần số 1 15rad / s . Nếu gắn vào nó một vật nhỏ có khối lượng m = 50g ở phía dưới trục và cách trục một khoảng l = 20cm, thì tần số dao động thành 2 10rad / s Tìm momen quán tính của con lắc này đối với trục dao động. 2 ĐS: 2 1 g / l 4 2 I ml 2 2 8.10 kg.m 1 2 Ta có: Mgx I x 2 1 I Mg 1 x là khoảng cách từ khối tâm của con lắc đến trục quay Khi gắn vật khối lượng m vào con lắc, PT vi phân của dao động điều hòa của con lắc: 2 2 d Mgx mgl I ml 2 dt d 2 g(Mx ml) 0 dt 2 I ml 2 g(Mx ml) g((I / g) 2 ml) 1 2 I ml 2 I ml 2 I 2 mgl 2 1 2 I ml 2 2 2 ml (2 g / l) 4 2 I 2 2 8.10 kg.m 1 2 2) Một bản mỏng đồng tính có dạng một tam giác đều với chiều cao h thực hiện các dao động bé xung quanh một trục nằm ngang trùng với một trong các cạnh của nó. Tìm chu kỳ dao động và độ dài rút gọn của con lắc này. ĐS: T 2h / g l h / 2 O G x y a dx mgOG h 2h ; OG ;a 0 I 3 3 m 1 h2 dI dm.x2 ;dm dS ; S ah S 2 3 y 2(h x) dS ydx;tg30o y 2(h x) 3 2m(h x)dx dm h2 2m h 1 I dI (hx2 x3 )dx mh2 2 h 0 6 2g 2h T 0 h 0 g II. DĐ CƠ TẮT DẦN I. PTDĐ cơ tắt dần: d 2 x m. F F k.x r.v dt 2 ñh c r là hệ số cản của môi trường dx k r thay : v ; 2 ;2 dt 0 m m ta được PTVP của DĐ cơ tắt dần d 2 x dx 2 2 x 0 dt2 dt 0 Khi nghiệm của nó có dạng: 0 t x A0 e cos(t ) Biên độ, tần số góc và chu kỳ của DĐ tắt dần: 2 A Ae .t ; 2 2 ; T t o 2 2 o Giảm lượng loga: giảm lượng loga của DĐ cơ tắt dần có trị số bằng loga tự nhiên của tỷ số của hai biên độ kế tiếp cách nhau mộx t chu kỳ T +A0 t At Aoe ln ln (t T ) At T Aoe 0 t T ln e T T - A0 Nếu 0 chuyển động này được gọi là quá tắt dần, dao động tử quá tắt dần ban đầu được dịch khỏi vị trí cân bằng sẽ chậm chạp tiến gần về vị trí cân bằng và không thể đi quá vị trí đó. Nếu 0 thì chuyển động được gọi là tắt dần tới hạn. Dao động tử tắt dần tới hạn không dao động mà tiến dần tới vị trí cân bằng nhanh hơn dao động tử quá tắt dần x (a) DĐ quá tắt dần A0 a (b) DĐ tắt dần tới hạn b t Ví dụ: Bài 1: Biên độ của dao động tắt dần sau thời gian t1= 20s giảm đi n1 = 2 lần. Hỏi sau thời gian t2 = 1 phút, nó giảm đi bao nhiêu lần? 1) t1 A0 t1 A1 A0e e n1 A1 A t2 0 t2 A2 A0e e A2 3 3t1 e n1 8 • Bài 2:Một đĩa đồng chất có bán kính R = 13cm có thể quay xung quanh một trục nằm ngang, vuông góc với mặt đĩa và đi qua mép đĩa. Tìm chu kỳ dao động bé của đĩa trong trọng trường của trái đất, nếu giảm lượng loga của sự tắt dần là 1 . 2) T T 2 2 2 2 0 0 T 2 2 2 2 2 2 4 0 2 T T T 0 mgR mgR 2g 0 3 I mR2 3R 2 3R T (4 2 2 ) 0,9 s 2g Bài 3: Xác định giảm lượng loga của con lắc toán chiều dài l = 50cm, biết rằng sau thời gian = 8 phút nó mất ... vuông góc với tia sóng. • Sóng dọc là sóng trong đó các phần tử của môi trường đàn hồi dao động dọc theo tia sóng. Thực nghiệm chứng tỏ rằng: sóng ngang chỉ có thể truyền trong chất rắn và bề mặt chất lỏng; sóng dọc có thể truyền trong chất rắn, lỏng và khí. 3. Các đại lượng đặc trưng cho sóng: a) Vận tốc sóng: là quãng đường mà sóng truyền được sau một đơn vị thời gian. Trong lí thuyết đàn hồi người ta chứng minh được trong môi trường đẳng hướng, vận tốc của sóng dọc: 1 E v , E 1/ , lần lượt là hệ số đàn hồi, suất đàn hồi (suất Young) và khối lượng riêng của môi trường. • Vận tốc của sóng ngang: G v G là suất trượt của môi trường b) Chu kỳ và tần số của sóng là chu kỳ và tần số của các phần tử dao động của môi trường. c) Bước sóng của sóng là quãng đường mà sóng truyền được sau khoảng thời gian một chu kỳ vT v / f II. Hàm sóng: Xét dao động của một đại lượng u (đại lượng dao động) lan truyền theo trục y. Giả sử tại điểm y = 0 , u biến thiên theo thời gian với quy luật : u = f(t) , y = 0 Vì dao động truyền đi nên ở một điểm M bất kỳ, tại thời điểm t, đại lượng u sẽ lấy các giá trị giống như ở O nhưng tại thời điểm y M x x t ' t O v y v là vận tốc truyền sóng Nói một cách khác : y u(y,t) u(0,t ') hayu(y,t) f (t ) v Sóng truyền theo một phương xác định và đặc trưng bằng các dao động xảy ra hoàn toàn giống nhau trên các mặt phẳng thẳng góc với phương truyền sóng được gọi là sóng phẳng chạy . Biểu thức trên mô tả sóng phẳng chạy theo trục y với vận tốc v gọi là hàm sóng. Sóng phẳng đơn sắc là sóng mà dao động tại mỗi điểm là dao động điều hoà Xét một sóng phẳng truyền theo phương Oy trùng với tia sóng. Giả sử dao động của phần tử nằm tại điểm O ứng với tọa độ y = 0 có dạng u A.cost Hàm sóng tại M: y 2 y u Acos t Acos(t ) v Nếu sóng truyền theo chiều ngược lại thì: y 2 y u Acos(t ) Acos(t ) v Đối với sóng cầu, biên độ của nó giảm tỷ lệ nghịch với khoảng cách nên PT sóng cầu : A y u k cos(t ) y v k là hệ số tỷ lệ phụ thuộc tính chất của môi trường Vậy u có tính chất tuần hoàn theo cả thời gian (với chu kỳ T 2 / ) và không gian (với chu kỳ λ = vT) Có thể biểu diễn hàm sóng dưới dạng số phức: 2 y i t u Ae 2 Đặt k n gọi là vecto sóng, n là vecto đơn vị hướng theo chiều truyền sóng r n thì: 2 y y kr kr cos O u M r là bán kính vecto vẽ tới điểm khảo sát dao động Do đó hàm sóng có thể viết: u Ae i(tk r) Hàm sóng là nghiệm của phương trình vi phân gọi là phương trình truyền sóng. Có thể tìm thấy dạng của phương trình sóng như sau: lấy đạo hàm hạng hai của u theo thời gian: 2 u 2 2 u Lấy đạo hàm hạnt g hai của u theo không gian: 2u 2u y2 v2 2u 1 2u Vậy: y2 v2 t 2 Đây là PT sóng đối với sóng truyền theo phương y Nếu sóng truyền trong khắp không gian thì phương trình sóng có dạng tổng quát: 1 2u u v2 t 2 2 2 2 u x2 y2 z2 là toán tử Laplace trong hệ toạ độ Descartes III. Năng lượng của sóng cơ 1. Năng lượng sóng: năng lượng sóng chứa trong thể tích dV gồm động năng và thế năng tương tác của các phần tử môi trường chứa trong thể tích đó. 2 y Giả sử hàm sóng có dạng: u Acos(t ) Người ta chứng minh được năng lượng sóng trong thể tích dV nằm trên phương truyền sóng y là: 2 y dW dV 2 A2 sin2 (t ) 2. Mật độ năng lượng sóng: dW 2 y w 2 A2 sin2 (t ) dV Mật độ năng lượng trung bình (giá trị trung bình của nó trong một chu kỳ) 1 w 2 A2 2 3. Vectơ Umốp – Pointing: Năng lượng sóng truyền theo chiều truyền sóng nên người ta đưa ra vectơ Umốp – Pointing: U w.v Vectơ này hướng theo chiều của vận tốc truyền sóng và có trị số bằng năng lượng sóng trung bình truyền qua một đơn vị diện tích đặt vuông góc với phương truyền sóng sau mỗi đơn vị thời gian. IV.Sóng âm 1. Khái niệm mở đầu: Sóng âm là các sóng cơ học có tần số trong khoảng từ 20Hz đến 20.000Hz mà thính giác của ta có thể nhận biết được. Những dao động cơ có tần số dưới 20Hz gọi là hạ âm, trên 20.000Hz gọi là siêu âm. Vận tốc truyền âm trong chất khí: RT C v ; p Cv R là hằng số khí lý tưởng là khối lượng 1 mol khí 2. Những đặc tính sinh lý của âm: Nhờ thính giác, con người có thể phân biệt được ba đặc tính sinh lý của âm là: độ cao, âm sắc và độ to. * Độ cao của âm do tần số của âm quyết định. * Âm sắc đặc trưng cho sắc thái của âm, nó cho ta biết âm thanh hay rè, trong hay đục. Âm sắc do đồ thị dao động của âm quyết định. * Độ to: để đặc trưng cho độ to người ta dùng hai đại lượng là cường độ âm và mức cường độ âm. Cường độ âm: là năng lượng sóng âm truyền qua một đơn vị diện tích đặt vuông góc với phương truyền sóng trong một đơn vị thời gian. Đơn vị là 2 (W/m ) 1 I vA2 2 2 Cường độ âm đặc trưng cho độ mạnh của âm về phương diện vật lý. Tuy nhiên độ to của âm không tỷ lệ thuận với cường độ âm. Tai người có thể nghe được âm có cường độ âm -12 2 nhỏ nhất Io = 10 W/m ứng với tần số 1000Hz gọi là ngưỡng nghe. Cường độ âm I = 10W/m2 gây cho tai ta cảm giác đau đớn không phụ thuộc tần số gọi là ngưỡng đau. • Độ to của âm đặc trưng cho độ mạnh của âm về phương diện sinh lý. Độ to của âm chỉ có ý nghĩa trong khoảng tần số từ 20Hz đến 20.000Hz mà tai người có thể nghe được. Độ to L của âm được xác định theo công thức : I I L(B) log hoặc L(dB) 10log I I0 0 I là cường độ âm mà ta muốn xác định độ to 12 2 I0 10 W / m là cường độ cơ sở Ví dụ: Bài 1: Nguồn của một sóng âm (coi như nguồn điểm) có công suất 1 W . Tìm cường độ và mức cường độ âm tại điểm cách nguồn 3m. Bài giải: • Cường độ âm: P 10 6 I 8,8.10 9 W / m2 4 r 2 4 .9 • Mức cường độ âm: I 8,8.10 9 L 10lg 10lg 12 39dB I0 10 • Bài 2: Một máy bay bay trên đầu ở độ cao 100m. Mức cường độ âm trên mặt đất khi máy bay bay qua đầu là 150dB. Hỏi độ cao mà máy bay phải bay để cho trên mặt đất mức cường độ âm không quá 120dB. Bỏ qua thời gian cần thiết để âm truyền đến mặt đất. Bài giải I1 I1 15 I1 15 L1 10lg 150 lg lg10 10 I0 I0 I0 P 15 15 2 2 10 P 10 4 r1 I0 4 r1 I0 I2 I2 12 I2 12 L2 10lg 120 lg lg10 10 I0 I0 I0 2 P 12 r1 3 2 3 2 7 2 10 2 10 r2 10 r1 10 4 r2 I0 r2 rmin 3160m V. Hiệu ứng Doppler: Là sự dịch chuyển tần số mà máy thu nhận được khi có sự dịch chuyển giữa nguồn âm và máy thu. Xét trường hợp phương chuyển động của nguồn âm và máy thu nằm dọc theo đường nối chúng và môi trường đứng yên. Gọi u là vận tốc chuyển động của nguồn âm A, u’ là vận tốc chuyển động của máy thu B, v là vận tốc truyền âm. x x A B u > 0 u’ > 0 Qui ước , nếu nguồn âm đi tới gần máy thu thì u > 0, đi xa máy thu thì u < 0, nếu máy thu đi tới gần nguồn âm thì u’ > 0, đi xa nguồn âm thì u’ < 0. 1 v v Ta có: f là số sóng âm truyền đi T vT trong một đơn vị thời gian, vì vậy muốn tính tần số của âm do máy thu nhận được, ta đi tính số sóng âm mà máy thu nhận được trong một đơn vị thời gian. Xét trường hợp tổng quát : nguồn âm và máy thu đều chuyển động . Giả sử nguồn âm và máy thu đi tới gặp nhau ( u > 0, u’ > 0). Vì máy thu đi tới gần nguồn âm nên có thể coi vận tốc truyền âm được tăng thêm một lượng u’ và bằng v’ = v + u’. Vận tốc truyền âm v chỉ phụ thuộc môi trường truyền âm mà không phụ thuộc chuyển động của nguồn âm, nên khi nguồn âm chuyển động thì v không thay đổi, mà chỉ có bước sóng của âm phát ra bị thay đổi . Vì ta biết rằng hai sóng liên tiếp phát ra cách nhau một khoảng thời gian bằng chu kỳ T thì sẽ cách nhau một đoạn v T . Nếu nguồn âm A đứng yên thì sau một khoảng thời gian bằng chu kỳ T sóng a do nguồn phát ra truyền đi được một đoạn v T . Vì vậy sóng b ( đường cong chấm chấm), do nguồn âm vừa phát ra phải cách sóng a một đoạn bằng bước sóng đó. Nhưng vì trong khoảng thời gian T này, nguồn A đã di chuyển được một đoạn uT thì sóng b (đường cong liền nét b’) vừa phát ra cách sóng A một đoạn ' uT u > 0 b a v b’ x x A B uT ' Như vậy có thể coi bước sóng do nguồn âm phát ra là '. Vậy tần số của âm mà máy thu nhận được trong trường hợp nguồn âm và máy thu đi tới gặp nhau: v ' v u ' v u ' f ' ' uT vT uT v u ' v u ' f T(v u) v u Ta có công thức tổng quát cho mọi trường hợp: v u, f ' f v u Chọn dấu ở tử số và mẫu số như sau: Khi nguồn âm lại gần máy thu, tần số tăng nên mẫu số lấy dấu trừ, khi nguồn âm ra xa máy thu, tần số giảm nên mẫu số lấy dấu cộng. Khi máy thu lại gần nguồn âm tần số tăng nên tử số lấy dấu cộng, khi máy thu ra xa nguồn âm tần số giảm nên tử số lấy dấu trừ. v u, u u’ f ' f S D v u v u, u u’ f ' f S D v u v u, u u’ f ' f S D v u v u, u u’ f ' f S D v u Ví dụ: 1) Hai tàu ngầm A và B chuyển động theo hướng đâm đầu vào nhau trong nước đứng yên. Tàu A chuyển động với tốc độ 50km/h, tàu B 70km/h. Tàu A phát đi một sóng âm có tần số 1000Hz. Vận tốc sóng âm trong nước là 5470km/h. Hỏi a) Tần số của tín hiệu do tàu B thu nhận. b) Tần số do tàu A thu nhận của tín hiệu phản xạ từ tàu B a) A là nguồn phát, B là máy thu v v 5470 70 f ' B f .1000 1022Hz v vA 5470 50 b) B là nguồn phát, A là máy thu v v 5470 50 f '' A f ' .1022 1044Hz v vB 5470 70 • Một quan sát viên đứng yên nhận các dao động âm từ hai cái âm thoa, một cái đang tiến lại gần còn cái kia đang lùi ra xa với cùng tốc độ. Khi đó quan sát viên nghe được phách có tần số f = 2Hz. Tìm tốc độ của mỗi âm thoa, nếu tần số dao động của chúng là f0 = 680Hz và vận tốc âm trong không khí là v = 340m/s • Gọi f1 là tần số QSV nhận được từ âm thoa tiến lại gần và f2 là tần số QSV nhận được từ âm thoa tiến ra xa, ta có: v v f f , f f 1 v u 0 2 v u 0 2uv f f f f 1 2 v2 u2 0 2u2 462400u 231200 0 u 0,5m / s • Bài tập: Một nguồn dao động âm có tần số f = 1700 Hz và một máy thu được đặt tại một điểm. Tại thời điểm t = 0 nguồn bắt đầu đi ra xa máy thu với gia tốc không đổi a = 10 m/s2 . Coi vận tốc của âm là v = 340 m/s, tìm tần số dao động mà máy thu đứng yên thu được sau t = 10s kể từ sau khi nguồn bắt đầu chuyển động. • ĐS: f f ' 1,35kHz 1 2at / v • Vì âm cần thời gian để truyền đến máy thu, nên tần số mà máy thu thu được sau 10s là tần số do nguồn âm phát ra tại thời điểm t1 < t, với: 1 at 2 v v2 2avt t 1 t t 1 2 v 1 a v v v f ' f f f v u v u v at1 v f f 1,35kHz v2 2avt 1 2at / v V.Sóng điện từ: Sóng điện từ là trường điện từ biến thiên truyền đi trong không gian. 1.PT sóng điện từ: Các PT Maxwell của SĐT trong môi trường không có điện tích và không có dòng điện: B rotE ; divB 0 t D rotH ; divD 0 t B rot rotE rot (rotB) t t rot rotE divE 2 E D 1 divE div divD 0 o o (rotB) (rot H ) (rotH ) t t o o t 2 D 2 E o t 2 o o t 2 2 E rot rotE 2 E o o t 2 2 E 2 E 0 o o t 2 Đặt: 1 v2 0 0 1 2 E 2 E 0 v2 t 2 Đây là phương trình truyền sóng của điện trường 1 v là vận tốc truyền SĐT 00 Tương tự PT truyền sóng của từ trường: 1 2 B 2 B 0 v2 t 2 1 3.108 m / s c là vận tốc truyền sóng điện 0 0 từ trong chân không c c Vậy: v n Với n là chiết suất của môi trường 3. Sóng ĐT phẳng đơn sắc: Là SĐT, trong đó trường chỉ phụ thuộc vào một tọa độ . Các mặt sóng là các mặt phẳng song song; nghĩa là phương truyền sóng là những đường song song và nguồn sóng coi như ở rất xa. Nếu sóng truyền theo phương của trục x thì các phương trình của trường có dạng: 2 E 1 2 E 0 x2 v2 t 2 2 B 1 2 B 0 x2 v2 t 2 Nghiệm của các PT trên là: x x E Em cos t ; B Bm cos t (1) v v (1) là phương trình của SĐT phẳng đơn sắc, nếu sóng truyền theo chiều ngược lại thì trong các PT trên thay x bằng –x Đối với SĐT phẳng đơn sắc, theo các PT Maxwell có thể chứng minh được: • a) E và H vuông góc nhau • b) E , H , v theo thứ tự đó tạo thành một tam diện thuận ba mặt vuông. y v E 0 x B z c) E , H luôn luôn dao động cùng pha, và có trị số tỷ lệ với nhau: B 0 E 0 H 0 0 E E B B 0 0 v 1 B (n E) v n là vecto đơn vị nằm theo phương truyền sóng 4. Năng lượng và năng thông SĐT: Mật độ năng lượng SĐT: .E 2 .H 2 w w w 0 0 E B 2 2 Đối với SĐT phẳng đơn sắc 2 2 0 E 0 H o E o H 2 2 w o E o H o E. o H Mật độ năng thông SĐT: P = w.v Đ ặt: P wv ; P gọi là vecto Umop – Pointing 1 P w.v E.H. E.H 0 o 0 o Vì E , H , v theo thứ tự tạo thành tam diện thuận nên: P E H Cường độ sóng điện từ : là một đại lượng có trị số bằng trị trung bình theo thời gian của mật độ năng thông tại một điểm. 2 I P w.v 0 E .v Đối với sóng điện từ phẳng đơn sắc 2 I P w.v o E .v y 1 E E cos(t ) E 2 E 2 m v 2 m 1 2 1 o 2 1 0 2 I o Em.v Em H m 2 2 0 2 o Ví dụ: Điện trường của một sóng điện từ phẳng được cho bởi 15 x Ex 0 ; Ey 0 ; Ez 2cos 10 (t ) c m c 3.108 s Sóng được truyền dọc theo chiều dương của trục x. Hãy viết các biểu thức cho các thành phần từ trường của sóng • Điện trường hướng theo trục z, sóng truyền theo chiều dương của trục x nên từ trường hướng theo trục y và điện trường và từ trường dao động cùng pha nên: 15 x Bx 0 ; By Bm cos 10 (t ) ; Bz 0 c E 2 B m 10 8 (T ) m c 3 • Một người quan sát ở cách một nguồn sáng điểm có công suất P = 250W là 1,8m. Tính các giá trị hiệu dụng của điện trường và từ trường do nguồn sáng gây ra tại vị trí của người quan sát. Coi nguồn bức xạ đều theo mọi hướng. • Cường độ sóng điện từ tại vị trí người quan sát: P 1 0 2 1 2 I 2 Em Ehd 4 r 2 0 c0 Pc V E 0 48 hd 4 r 2 m E B hd 1,6.10 7 T hd c Ví dụ:Một SĐT truyền theo chiều y âm. Tại một vị trí và một thời điểm, điện trường hướng dọc theo trục z dương và có độ lớn 100 V/m. Hỏi chiều và độ lớn của từ trường tại vị trí và thời điểm đó. Bài giải: 1 Vì: B n , E nên B hướng theo chiều âm c của trục x và có độ lớn: E 100 B 33,3.10 8 T c 3.108 z E B v y x • Vecto cường độ điện trường của một trường điện từ có dạng: 8 E(z,t) 15cos(6 t 4 z.10 )ex Viết biểu thức vecto cường độ từ trường • Điện trường hướng theo trục x, sóng truyền theo trục z, nên từ trường hướng theo trục y. Điện trường và từ trường dao động cùng pha. E B m ; 4 .10 8 v 1,5.108 m v v 4 8 8 5.10 Bm 5.10 H m 0 8 5.10 8 H (z,t) cos(6 t 4 z.10 )e y 0
File đính kèm:
 bai_giang_vat_ly_dai_cuong_a2_chuong_2_dao_dong_song.pdf
bai_giang_vat_ly_dai_cuong_a2_chuong_2_dao_dong_song.pdf

