Bài giảng Vật lý đại cương A2 - Chương 1: Trường điện từ
Luận điểm thứ hai của Maxwell. Dòng điện dịch
1. Phát biểu luận điểm: Bất cứ một điện trường
nào biến đổi theo thời gian cũng sinh ra một từ
trường.
2. Phương trình Maxwell- Ampere (M- A)
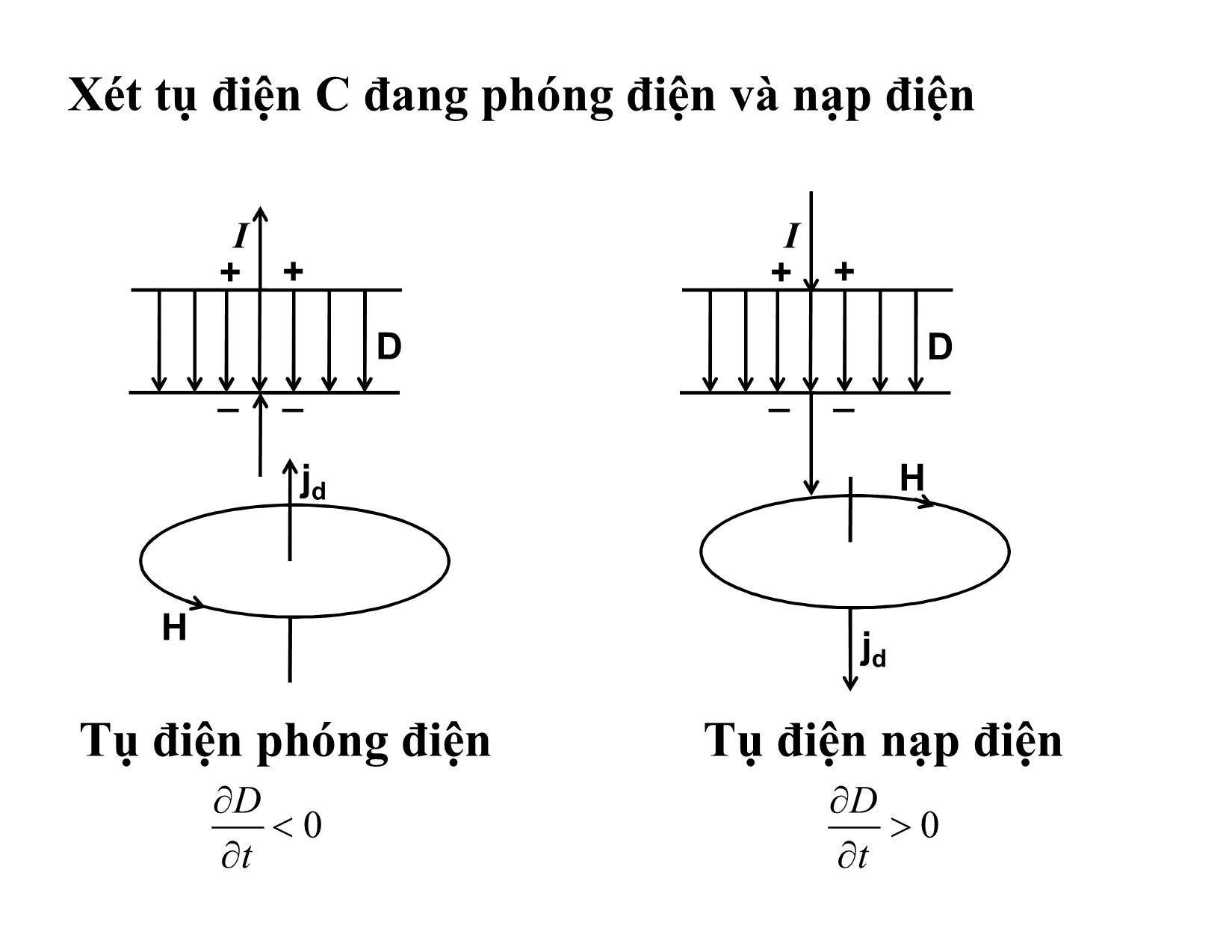
a) Giả thuyết của Maxwell về dòng điện dịch:
Dòng điện dịch là dòng điện tương đương với điện
trường biến đổi theo thời gian về phương diện sinh
ra từ trường.
Maxwell đã đặt một giả thuyết về phương chiều
và độ lớn của dòng diện dịch đó.b) Biểu thức của mật độ dòng diện dịch:
Theo Maxwell điện trường biến đổi giữa hai bản tụ
sinh ra từ trường giống như một dòng điện (dòng
điện dịch)chạy qua toàn bộ không gian giữa hai
bản của tụ điện, có chiều là chiều của dòng điện
dẫn trong mạch, và có cường độ bằng cường độ
dòng điện dẫn trong mạch đó.
Gọi Id là cường độ dòng điện dịch chạy giữa hai
bản tụ, I là cường độ dòng điện dẫn, S là diện tích
của mỗi bản thì mật độ dòng điện dịch giữa hai
bản tụ là:

Trang 1
Trang 2
Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Vật lý đại cương A2 - Chương 1: Trường điện từ

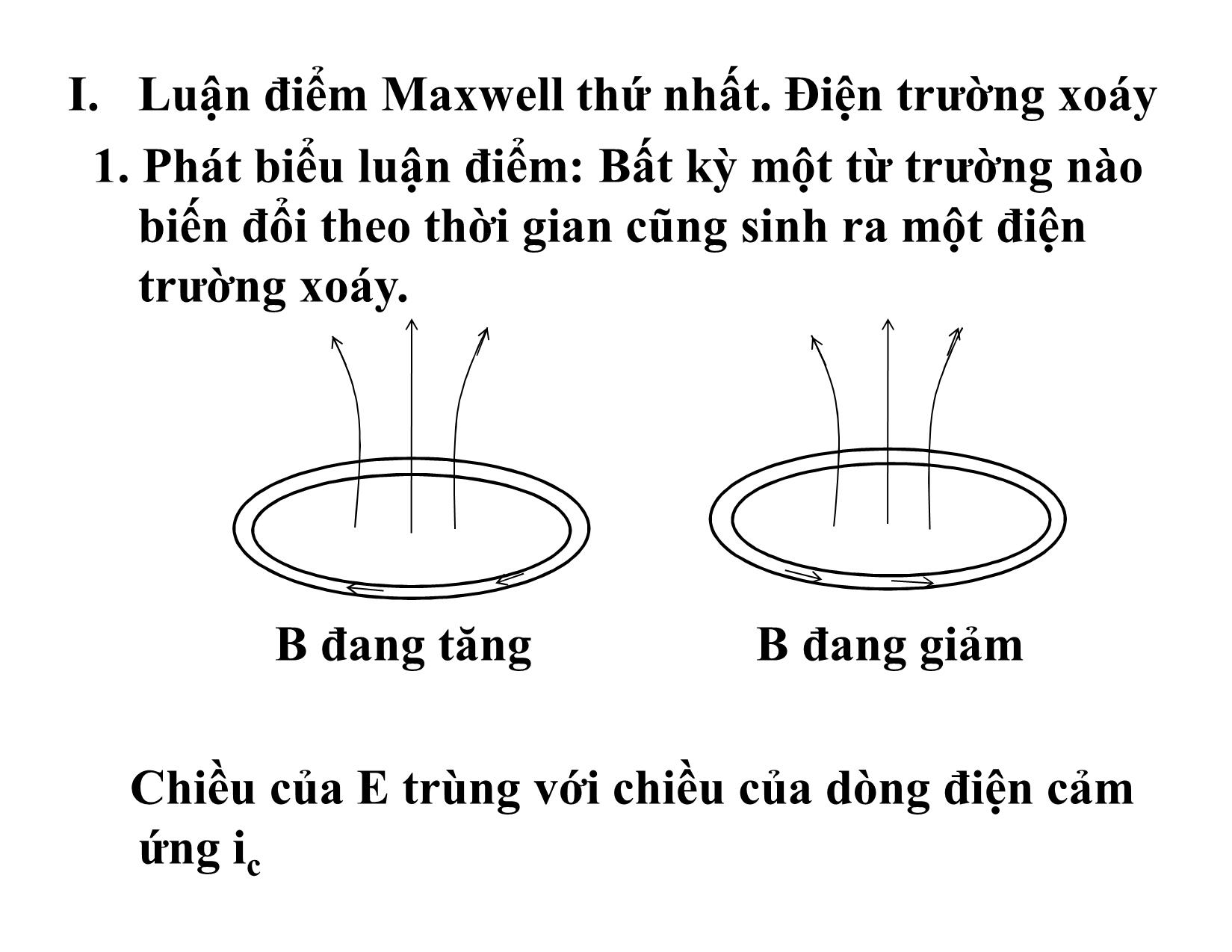
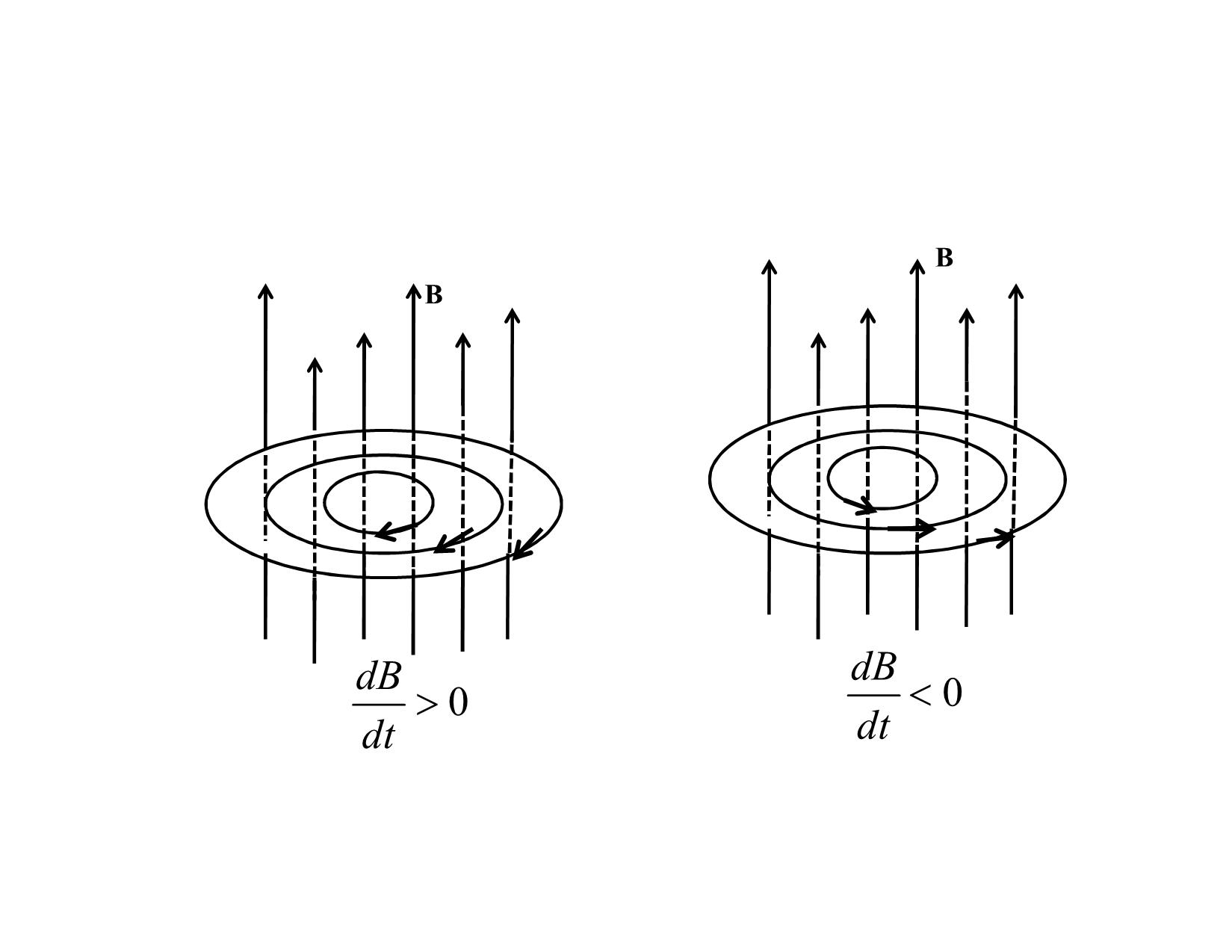
CHƯƠNG I TRƯỜNG ĐIỆN TỪ I. Luận điểm Maxwell thứ nhất. Điện trường xoáy 1. Phát biểu luận điểm: Bất kỳ một từ trường nào biến đổi theo thời gian cũng sinh ra một điện trường xoáy. B đang tăng B đang giảm Chiều của E trùng với chiều của dòng điện cảm ứng ic B B dB dB 0 0 dt dt 2. Phương trình Maxwell – Faraday (M-F) Xét một vòng dây dẫn khép kín (C) nằm trong một từ trường B đang biến đổi. Theo định luật cơ bản của hiện tượng cảm ứng điện từ, suất điện động cảm ứng xuất hiện trong vòng dây: d d m ( B.d S) (1) c dt dt S Theo định nghĩa của suất điện động: B dS S E.dl (2) c C E (C) + So sánh (1) và (2) ta được: d E.dl ( B.d S) C dt S Đây là phương trình M-F dạng tích phân Trong giải tích vectơ, người ta chứng minh được: E.dl rotE.d S Mà: C S d d B d B ( B.d S) ( )d S rotE dt S S dt dt Vì chỉ có từ trường biến đổi theo thời gian mới sinh ra điện trường xoáy, nên dấu đạo hàm toàn phần theo thời gian được thay bằng dấu đạo hàm riêng phần theo thời gian, nghĩa là ta có: B rotE t Đây là phương trình M-F dạng vi phân II. Luận điểm thứ hai của Maxwell. Dòng điện dịch 1. Phát biểu luận điểm: Bất cứ một điện trường nào biến đổi theo thời gian cũng sinh ra một từ trường. 2. Phương trình Maxwell- Ampere (M- A) a) Giả thuyết của Maxwell về dòng điện dịch: Dòng điện dịch là dòng điện tương đương với điện trường biến đổi theo thời gian về phương diện sinh ra từ trường. Maxwell đã đặt một giả thuyết về phương chiều và độ lớn của dòng diện dịch đó. b) Biểu thức của mật độ dòng diện dịch: Theo Maxwell điện trường biến đổi giữa hai bản tụ sinh ra từ trường giống như một dòng điện (dòng điện dịch)chạy qua toàn bộ không gian giữa hai bản của tụ điện, có chiều là chiều của dòng điện dẫn trong mạch, và có cường độ bằng cường độ dòng điện dẫn trong mạch đó. Gọi Id là cường độ dòng điện dịch chạy giữa hai bản tụ, I là cường độ dòng điện dẫn, S là diện tích của mỗi bản thì mật độ dòng điện dịch giữa hai bản tụ là: I I j d d S S Mà: dq 1 dq d q d dD I jd dt S dt dt S dt dt Vecto cảm ứng điện D luôn hướn g từ bản dương sang bản âm, khi tụ nạp điện , j cùng chiều với d D , và D tăn g, khi tụ phóng điện, j d ngược chiều với và D giảm nên có thể viết : D d D j d dt Vì chỉ có điện trường biến đổi theo thời gian mới sinh ra từ trường nên viết lại: D j d t Xét tụ điện C đang phóng điện và nạp điện I I + + + + D D _ _ _ _ jd H H jd Tụ điện phóng điện Tụ điện nạp điện D D 0 0 t t Bản chất của dòng điện dịch: E Trong chân không D E j như vậy 0 d 0 dt dòng điện dịch trong chân không về bản chất chỉ là điện trường biến đổi theo thời gian. E P Trong chất điện môi D E P j e 0 e d 0 dt t Vậy trong chất điện môi, mật độ dòng điện dịch gồm hai thành phần: thành phần thứ nhất là mật độ dòng điện dịch trong chân không, thành phần thứ hai là mật độ dòng điện phân cực. Dòng điện phân cực có liên quan đến sự quay của các lưỡng cực phân tử hoặc sự dịch chuyển của các trọng tâm của các phân tử không phân cực dưới tác dụng của điện trường ngoài. c) Phươ ng trình M axwell-Ampere (M-A): D Gọi j và j là vecto mật độ dòng điện dẫn d dt và dòng điện dịch tại một điểm thì vecto mật độ dòng điện toàn phần tại điểm đó là: D j j tp dt Xét một đường cong (C) nằm trong miền không gian có dòng điện dịch và dòng điện dẫn chạy qua. Theo định lý Ampere ta có: Đây là PT M-A D H.dl I j .d S tp dạng tích phân C S dt Từ PT trên ta suy ra phương trình M-A dạng vi phân: D rotH j dt III. Trường điện từ và hệ PT Maxwell 1. Trường điện từ: Điện trường và từ trường đồng thời tồn tại trong không gian tạo thành một môi trường thống nhất gọi là trường điện từ. Trường điện từ có năng lượng. Mật độ năng lượng trường điện từ bằng tổng mật độ năng lượng của điện trường và từ trường: 1 1 w w w ( E 2 H 2 ) (ED BH ) e m 2 0 0 2 Năng lượng trường điện từ: 1 W wdV ( E 2 H 2 )dV 0 0 V 2 V 1 (ED BH )dV 2 V 2. Hệ PT Maxwell dạng tích phân: B a) E.dl .d S t C S b) B.d S 0 S D c) H.dl j .d S C S dt d) D.d S Q S 3) Hệ PT Maxwell dạng vi phân: B a) rotE b) divD t D c) rotH j d) divB 0 dt Ngoài ra nếu môi trường đồng chất và đẳng hướng thì ta có các phương trình liên hệ cho trường với tính chất của môi trường D 0 E , j E , B 0 H • Ví dụ: Một tụ điện phẳng, bản cực hình tròn bán kính R được tích điện a) Tìm biểu thức của từ trường cảm ứng ở các điểm bán kính r khác nhau trong trường hợp r R ; r R Tính B khi r = R b) Tính dòng điện dịch Cho R = 55mm và dE/dt = 1,5.1012 V/ms a) Giữa các bản cực không có dòng điện dẫn nên dE Bdl I j S S 0 d 0 d 0 0 (C) dt dE B.2 r S 0 0 dt 1 dE r R : S r 2 B r 2 0 0 dt R2 dE r R : S R2 B 0 0 2r dt • Tại r = R B 4 .10 7.8,86.10 12.55.10 3.1,5.1012 459nT • b) dE i S. j S d d 0 dt .(55.10 3 )2.8,86.10 12.1,5.1012 126mA Ví dụ: Một tụ điện phẳng song song cấu tạo bởi hai bản cực tròn bán kính R = 18cm, nối với nguồn sức điện động 2 2 0 s i n 1 3 0 t ( V ) giá trị lớn nhất của dòng điện dịch là idmax = 7,6μA. Bỏ qua sự loang của điện trường ra bên ngoài mép của bản cực. a) Tính giá trị lớn nhất của dòng điện i. b) Tính giá trị lớn nhất của d E / d t . c)Tính khoảng cách d giữa các bản cực. d) Tính giá trị lớn nhất của B ở miền giữa hai bản cực, và cách tâm một khoảng r = 11cm a)imax = idmax = 7,6μA b) E E.A dD dE d j 0 E d dt 0 dt Adt A. j d d E 0 dt 6 dE id max 7,6.10 12 860 KVm / s dt max 0 8,86.10 c) U 220sin130t E d d dD dE cos130t j 220.130 d dt 0 dt 0 d 220.130 A. 220.130 j 0 A. j 0 d max d d max d 2 4 12 A.0 28600 3.14.18 .10 .8,86.10 28600 d 6 id max 7,6.10 3,39mm d) Giữa hai bản tụ không có dòng điện dẫn nên PT Ampere dạng tích phân là d D d E B.dl .d S .d S 0 0 0 (C) (S ) dt (S ) dt d d dE B.2 r E.d S (E r 2 ) r 2 0 0 0 0 0 0 dt (S ) dt dt 1 dE Bmax 00r 2 dt max 1 220.130 4 .10 7.8,86.10 12.11.10 2. 5,16 pT 2 3,39.10 3
File đính kèm:
 bai_giang_vat_ly_dai_cuong_a2_chuong_1_truong_dien_tu.pdf
bai_giang_vat_ly_dai_cuong_a2_chuong_1_truong_dien_tu.pdf

