Bài giảng Vật lý đại cương 2 - Chương 4: Thuyết tương đối hẹp - Phạm Thị Hải Miền

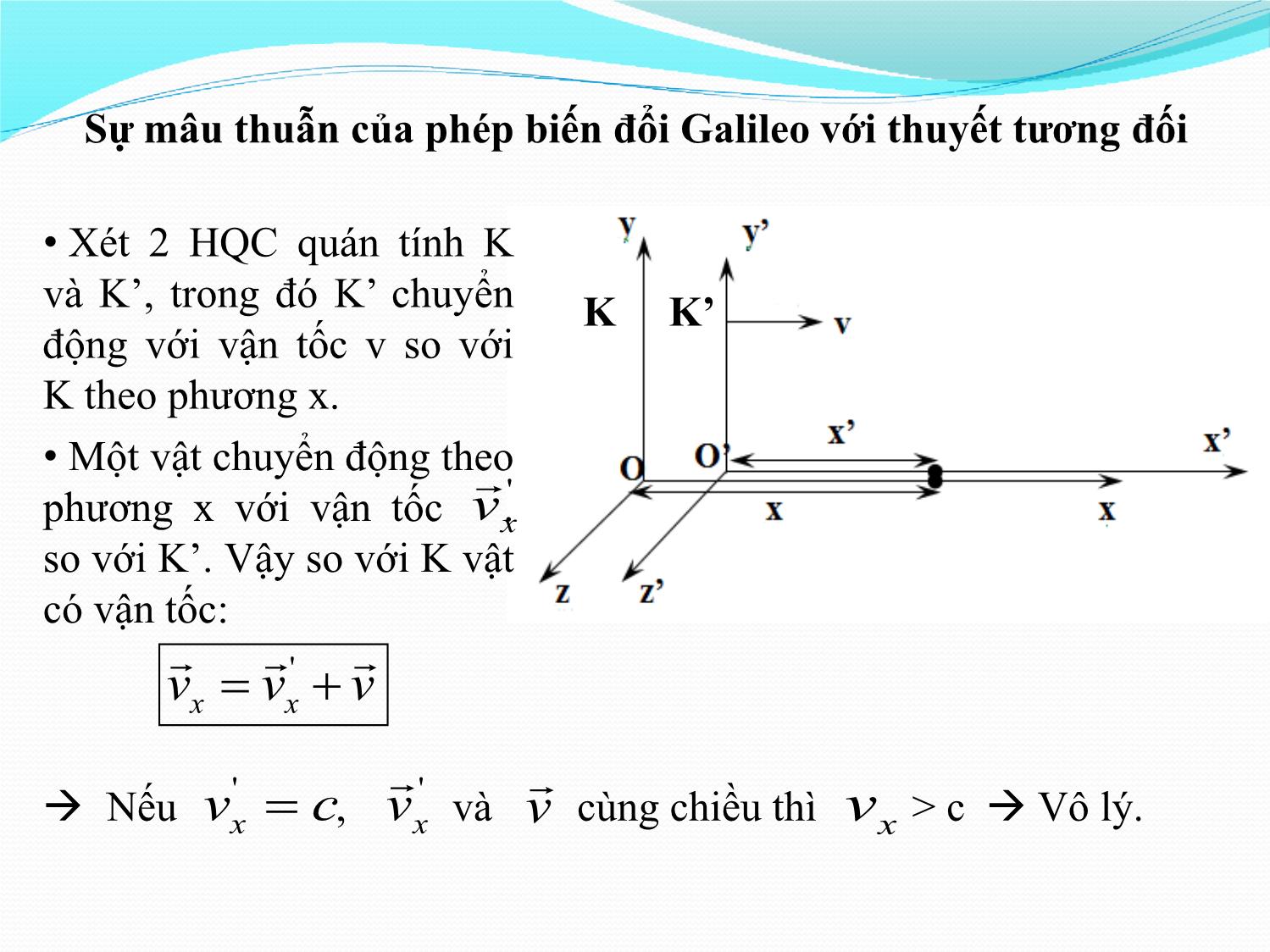
 CHƢƠNG 4
 THUYẾT TƢƠNG ĐỐI HẸP
1. Các tiên đề của thuyết tƣơng đối hẹp
2. Phép biến đổi Lorentz
3. Các hệ quả của phép biến đổi Lorentz
4. Động lực học tƣơng đối
 1. CÁC TIÊN ĐỀ CỦA THUYẾT TƢƠNG ĐỐI HẸP
 Thuyết tương đối hẹp được xây
dựng dựa trên hai tiên đề của
Einstein:
1. Nguyên lý tƣơng đối: Mọi định
 luật vật lý đều giống nhau trong các
 hệ qui chiếu quán tính.
2. Nguyên lý về sự bất biến của vận
 tốc ánh sáng: Vận tốc ánh sáng
 trong chân không là như nhau đối
 với mọi hệ qui chiếu quán tính.
 c = 3.108 m/s
 Sự mâu thuẫn của phép biến đổi Galileo với thuyết tƣơng đối
• Xét 2 HQC quán tính K
và K’, trong đó K’ chuyển K K’
động với vận tốc v so với
K theo phương x.
• Một vật chuyển động theo
 '
phương x với vận tốc vx.
so với K’. Vậy so với K vật
có vận tốc:
 ' 
 vxx v v
 ' ' 
 Nếu vcx , v x và v cùng chiều thì vx > c Vô lý.
 2. PHÉP BIẾN ĐỔI LORENTZ
 Lorentz (v~c)
 1
Galileo (v << c) Đặt  
 v2
 1 
 c2
 x = x’+ vt x  ( x ' vt ')
 x’= x – vt x'()  x vt
 y = y’ y = y’
 z = z’ z = z’
 v v
 t  ( t ' x ') t'()  t x
 t = t’ c2 c2
 Galileo (v << c) Lorentz (v~c) 
 vv 
 ’ vv'x x
 vx = vx + v v , v x 
 x v v
 1 v
 ’ 1' 2 v x 2 x
 vx = vx - v c c
 v' vy
 v y v ' 
 ’ y , y v
 vy = vy v
  (1 v ' )  (1 2 vx )
 c2 x c
 v
 v'z v' z
 ’ vz , z
 vz = vz v v
  (1 v ' )  (1 2 vx )
 c2 x c
Lưu ý: Các đại lượng v trong công thức là hình chiếu nên có giá trị đại số.
 BÀI TẬP VÍ DỤ 1
Hai hạt chuyển động ngược chiều nhau dọc theo một đường thẳng với
các tốc độ vc1 0,65 và vc2 0,85 đối với phòng thí nghiệm, với c
là vận tốc ánh sáng trong chân không. Tìm tốc độ của hạt thứ nhất đối
với hạt thứ hai.
 Hƣớng dẫn giải
 vv' 
 • Sử dụng công thức cộng vận tốc: v x
 x v
 1' v
 c2 x
• Xem phòng thí nghiệm như hệ K’, hạt thứ hai như hệ K
 Hạt thứ nhất chuyển động với vận tốc vv' đối với hệ K’
 x 1
 Hệ K’ chuyển động với vận tốc vv 2 đối với hệ K
• Theo đề: vv vv' 
 12 x vv 
 vc 120,97
• Vận tốc hạt thứ nhất đối với hệ K: 1/2 vv
 1 12
 c2
 3. CÁC HỆ QUẢ CỦA PHÉP BIẾN ĐỔI LORENTZ
 a. Tính tƣơng đối của sự đồng thời. Quan hệ nhân quả.
Giả sử trong hệ K có 2 biến cố A và B xảy ra đồng thời vào thời điểm
t tại 2 vị trí x1 và x2, nghĩa là t t12 t 0 . Thời điểm xảy ra
biến cố được ghi nhận trong hệ K’ sẽ là:
 vv v
 t x t x x x 
 cc2212 c2 1 2
 tt','12 t' t'2 t'1 
 vv22 v2
 11 1 
 cc22 c2
 Vì x12 x t 0 Sự đồng thời có tính tƣơng đối.
 Quan hệ nhân quả
• Trong hệ K: gọi biến cố A (x1, t1) là nguyên nhân và biến cố B
 (x2, t2) là kết quả.
 x x
 u 2 1 - vận tốc truyền tác dụng từ nguyên
 nhân đến kết quả
 t 2 t1
• Trong hệ K’:
 v v v
 t''()()()()2 t 1  t 2 x 2  t 1 x 1  t 2 t 1 x 2 x 1
 c2 c 2 c 2
 vv
 (t2 t 1 ) u ( t 2 t 1 ) (1 u ) t 2 t 1 
 cc22
 Nếu t2 > t1 thì t’2 > t’1 
 Thứ tự của các biến cố có quan hệ nhân quả không thay đổi
trong mọi hệ qui chiếu quán tính.
 b. Tính tƣơng đối của không gian
 (Sự co lại của độ dài)
• Xét một thanh nằm yên trong hệ K’ dọc theo trục x’ có chiều dài:
 ’ ’
 l o = x2 - x1
• Trong hệ K thanh có chiều dài l = x2 – x1
• Từ phép biến đổi Lorentz ta có:
 2
 xx21 v
 xx''21 l l 1 
 v2 o c2
 1 
 c2
 Độ dài dọc theo phƣơng chuyển động của thanh đo đƣợc
 trong hệ mà thanh chuyển động ngắn hơn độ dài của nó đo
 đƣợc trong hệ mà nó đứng yên.
 BÀI TẬP VÍ DỤ 2
Một tam giác đều đứng yên trong có diện tích là S0 . Trong HQC K
chuyển động với vận tốc v đối với tam giác và dọc theo một trong các
đường trung bình của nó, diện tích tam giác bằng bao nhiêu?
 Hƣớng dẫn giải
• Diện tích tam giác khi đứng yên:
 1
 S AH. BC
 0 2
• Giả sử tam giác chuyển động dọc theo
cạnh BC cạnh BC bị co lại, còn đường
cao AH không đổi độ dài. Diện tích S:
 11v2
 S AH. B ' C ' AH . l 1 
 220 c2
 v2
 SS 1
 0 c2
 c. Tính tƣơng đối của thời gian
 (Sự giãn ra của thời gian)
 ' '
 • Xét một biến cố xảy ra trong hệ K’ từ thời điểm t1 đến thời điểm t2
 Khoảng thời gian xảy ra biến cố trong hệ K’ là: 
 '''
 t t21 t
 • Trong hệ K, khoảng thời gian xảy ra biến cố là:
 t t21 t
 v v
 t' x' t' x' t '
 2 2 1 2 tt '
 c c 2
 t t 2 t1 v
 v2 v2 1 
 1 1 c2
 c2 c2
 Khoảng thời gian riêng nhỏ hơn khoảng thời gian ghi đƣợc
 trong hệ qui chiếu mà hạt chuyển động.
 (Thời gian riêng là thời gian đo bởi đồng hồ gắn liền với vật chuyển
 động)
 BÀI TẬP VÍ DỤ 3
Đồng hồ trong HQC K chuyển động rất nhanh so với trái đất cứ sau 5 s
(đo theo đồng hồ trên trái đất) nó bị chậm 0,1 s. Tìm vận tốc của K.
 Hƣớng dẫn giải
 • Khoảng thời gian đồng hồ trên trái đất đo được:
 ts5
 • Khoảng thời gian đồng hồ trên HQC K đo được:
 ts0 4,9
 • Theo thuyết tương đối:
 t
 t 0 v 0,6.108 m / s
 v2
 1 
 c2
 d. Sự bất biến của khoảng không – thời gian
Một biến cố trong không gian 4 chiều được xác định bởi 4 tọa độ
x, y, z, t và người ta định nghĩa khoảng không – thời gian giữa 2
biến cố như sau:
 s2 c t 2 x2 y2 z2 
 s2 s'2
 Khoảng không – thời gian là một đại lƣợng bất biến
 4. ĐỘNG LỰC HỌC TƢƠNG ĐỐI
a. Khối lƣợng tƣơng đối tính.
• Xét vật trong hệ K’ có khối lượng m0 gọi là khối lƣợng nghỉ. 
• Trong hệ K vật có khối lượng:
 m
 m o
 v2
 1 
 c2
b. Phƣơng trình cơ bản của chuyển động chất điểm.
 d mv 
 F 
 dt
c. Năng lƣợng tƣơng đối tính.
 • Năng lượng của một vật đứng yên gọi là năng lƣợng nghỉ: 
 2
 Eoo m c
 2
 • Năng lượng của một vật chuyển động: E mc
 m v
 • Động lượng của vật: P o
 v2
 1 
 c2
 2
 • Động năng của vật: W()do m m c
 2 2 4 2 2
 • Liên hệ giữa P và E: E mo c p c
 BÀI TẬP VÍ DỤ 4
Một electron chuyển động với tốc độ v=0,5c. Tìm tỉ số động năng và
năng lượng nghỉ của electron.
 Hƣớng dẫn giải
 • Động năng electron:
 2m0 2 2 1
 Wdo (m m ) c ( m00 ) c m c ( 1)
 vv22
 11 
 cc22
 • Tỉ số động năng và năng lượng nghỉ:
 2 1
 mc0 ( 1)
 v2
 1 
 W 2 1
 d c ( 1) 0,155
 2 2
 E00 m c v
 1 
 c2