Bài giảng Vật lý đại cương 1 - Chương 8: Điện môi
Hiện tượng phân cực điện môi
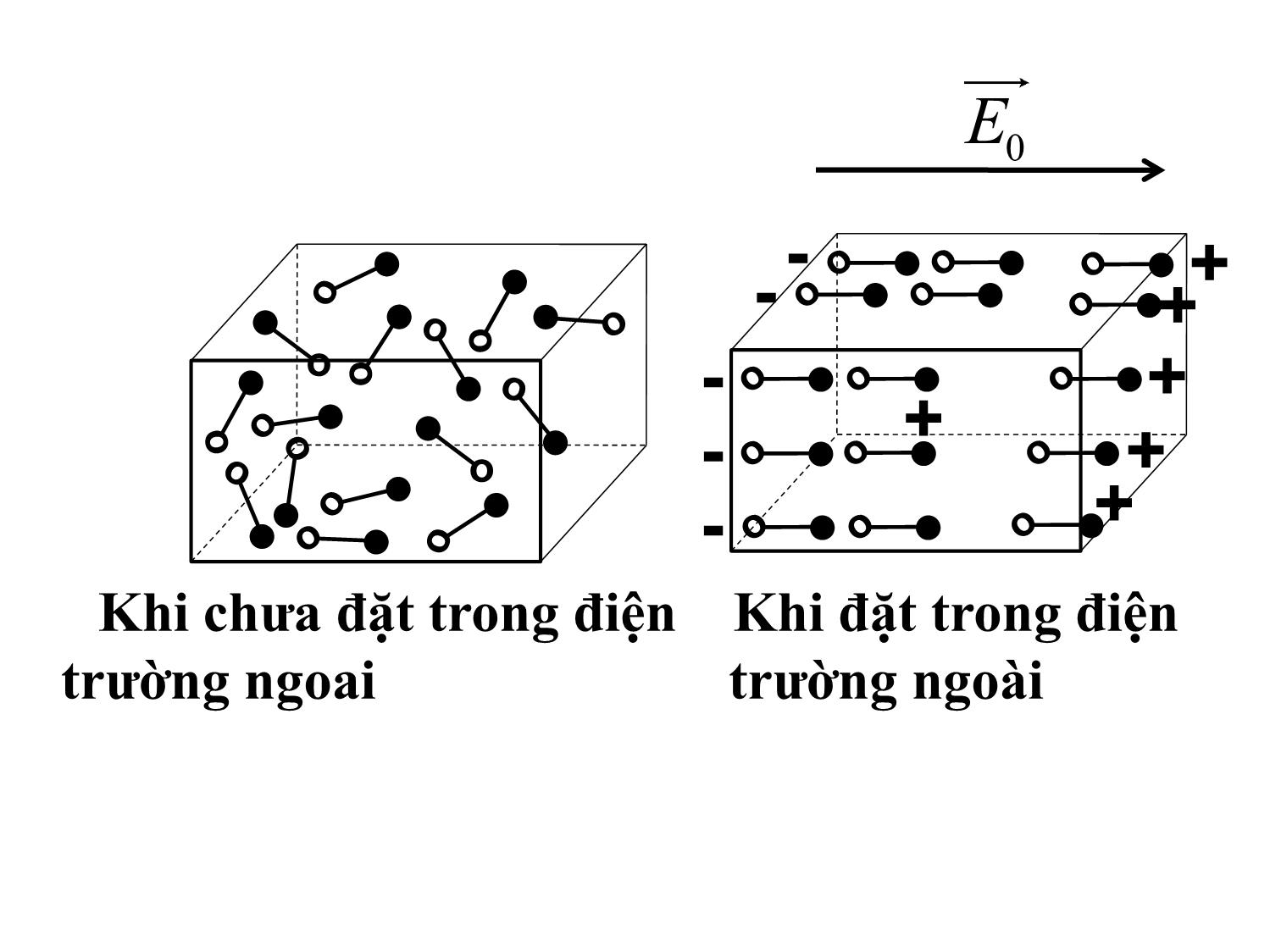
Theo vật lý cổ điển, điện môi là môi trường chất
không có các điện tích tự do, dưới tác dụng của
điện trường ngoài các điện tích bên trong nó chỉ
có thể dịch chuyển những khoảng cách nhỏ vào
cở kích thước của nguyên tử. Do đó tính dẫn điện
của điện môi rất kém có thể coi là chất không dẫn
điện. Khi đặt khối điện môi đồng chất và đẳng
hướng BC vào trong điện trường ngoài thì trên
các mặt giới hạn của thanh điện môi sẽ xuất hiện
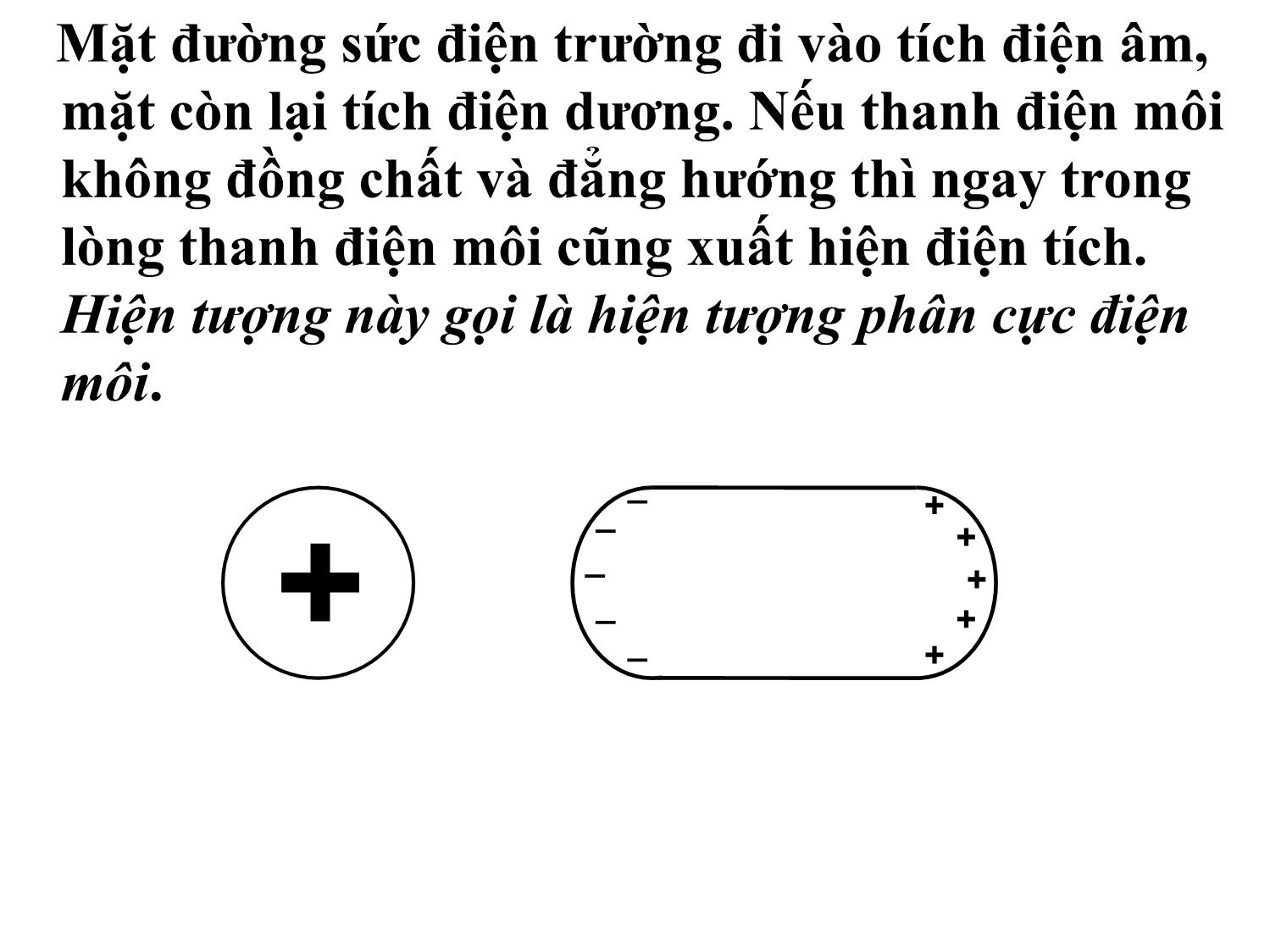
các điện tích trái dấu nhau. Hiện tượng này gọi là
hiện tượng phân cực điện môi.Mặt đường sức điện trường đi vào tích điện âm,
mặt còn lại tích điện dương. Nếu thanh điện môi
không đồng chất và đẳng hướng thì ngay trong
lòng thanh điện môi cũng xuất hiện điện tích.
Hiện tượng này gọi là hiện tượng phân cực điện
môi.

Trang 1

Trang 2
Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8

Trang 9
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Vật lý đại cương 1 - Chương 8: Điện môi

Chương VIII ĐiỆN MÔI I.Sự phân cực của chất điện môi 1. Hiện tượng phân cực điện môi Theo vật lý cổ điển, điện môi là môi trường chất không có các điện tích tự do, dưới tác dụng của điện trường ngoài các điện tích bên trong nó chỉ có thể dịch chuyển những khoảng cách nhỏ vào cở kích thước của nguyên tử. Do đó tính dẫn điện của điện môi rất kém có thể coi là chất không dẫn điện. Khi đặt khối điện môi đồng chất và đẳng hướng BC vào trong điện trường ngoài thì trên các mặt giới hạn của thanh điện môi sẽ xuất hiện các điện tích trái dấu nhau. Hiện tượng này gọi là hiện tượng phân cực điện môi. Mặt đường sức điện trường đi vào tích điện âm, mặt còn lại tích điện dương. Nếu thanh điện môi không đồng chất và đẳng hướng thì ngay trong lòng thanh điện môi cũng xuất hiện điện tích. Hiện tượng này gọi là hiện tượng phân cực điện môi. _ _ + + _ + _ + + _ + Hiện tượng phân cực điện môi bề ngoài giống hiện tượng điện hưởng trong vật dẫn kim loại, song về bản chất, hai hiện tượng hoàn toàn khác nhau. Trong hiện tượng phân cực điện môi, ta không thể tách riêng các điện tích để chỉ còn một loại điện tích; trên thanh điện môi các điện tích ở đâu sẽ định xứ ở đó, không dịch chuyển tự do được; vì vậy chúng được gọi là các điện tích liên kết. Các điện tích liên kết sẽ gây ra điện trường phụ E ' Điện trường tổng hợp trong điện môi là: E E0 E' E 0 là điện trường ngoài tạo nên sự phân cực của khối điện môi. 2.Giải thích hiện tượng phân cực điện môi Mỗi phân tử ( hay nguyên tử ) gồm các hạt nhân mang điện tích dương và các electron mang điện tích âm chuyển động rất nhanh xung quanh hạt nhân. Khi xét ở những khoảng cách lớn so với kích thước phân tử ta có thể coi tác dụng của các electron trong phân tử tương đương với tác dụng của điện tích tổng cộng –q của chúng đặt tại một điểm nào đó trong phân tử. Điểm này gọi là “trọng tâm “của các điện tích âm. Tương tự như vậy đối với hạt nhân ta cũng có “trọng tâm” của các điện tích dương. * Phân tử không phân cực là phân tử có phân bố electron đối xứng xung quanh hạt nhân. Vì thế khi chưa đặt trong điện trường ngoài trọng tâm điện tích âm và dương trùng nhau, phân tử không phải là lưỡng cực điện, mômen điện của nó bằng không. Khi đặt phân tử không phân cực vào trong điện trường ngoài,các trọng tâm điện âm và dương dịch chuyển ngược chiều nhau, phân tử trở thành một lưỡng cực điện có momen điện khác không. Người ta đã chứng minh được: pe 0 E 0 là hằng số điện, α gọi là độ phân cực của phân tử Vì khoảng cách giữa trọng tâm điện tích dương và âm của mỗi phân tử trong trường hợp này phụ thuộc điện trường tổng hợp nên các lưỡng cực xuất hiện được gọi là các lưỡng cực đàn hồi. Sự phân cực này gọi là phân cực điện tử. * Phân tử phân cực là loại phân tử có phân bố electron không đối xứng xung quanh hạt nhân. Vì thế ngay khi chưa đặt trong điện trường ngoài, các trọng tâm điện tích âm và dương cũng không trùng nhau nên phân tử là một lưỡng cực điện có mômen điện khác không. Điện trường ngoài hầu như không ảnh hưởng đến độ lớn của mômen điện nên các lưỡng cực này gọi là lưỡng cực cứng. Tác dụng chủ yếu của điện trường ngoài đối với các phân tử loại này là là làm quay và định hướng lưỡng cực điện theo chiều song song với điện trường. Sự phân cực này gọi là phân cực định hướng. Tuy mômen điện của phân tử khác không nhưng do chuyển động nhiệt nên chúng sắp xếp hỗn loạn nên hiện tượng phân cực điện môi không xảy ra.Chính sự sắp xếp có định hướng của các lưỡng cực điện của mỗi phân tử khi đặt nó trong điện trường ngoài làm xuất hiện các điện tích trái dấu trên bề mặt khối điện môi (hình vẽ). E0 - + - + o - + + o - + - + Khi chưa đặt trong điện Khi đặt trong điện trường ngoai trường ngoài Nếu khối điện môi không đồng chất thì trong lòng khối điện môi cũng xuất hiện các điện tích. * Đối với điện môi tinh thể, mạng các ion dương và các ion âm coi như lồng vào nhau. Dưới tác dụng của điện trường ngoài các mạng tinh thể dương và các mạng tinh thể âm dịch chuyển theo hai chiều ngược nhau và tạo ra sự phân cực của chất điện môi. Sự phân cực này gọi là phân cực ion. II. Vectơ phân cực n 1. Định nghĩa: pei i 1 Pe V p ei và n là vectơ momen điện và số phân tử trong thể tích vô cùng bé ∆V. Đối với điện môi không phân cực đặt trong điện trường đều thì mọi phân tử đều có cùng p ei nên n.p P e n .p e V 0 e n n là mật độ phân tử (là số phân tử trong 0 V một đơn vị thể tích) Gọi E là vectơ CĐĐT tổng hợp trong khối điện môi, ta có : P n p n E E e 0 e 0 0 0 e Với e n 0 là hệ số phân cực trong một đơn vị thể tích ( độ cảm điện môi) Đối với điện môi tinh thể, P e cũng liên hệ với bởi công thức trên. 3. Liên hệ giữa vectơ phân cực điện môi và mật độ điện tích liên kết. a) Liên hệ giữa vectơ phân cực điện môi và mật độ điện tích mặt Ta tưởng tượng tách ra trong điện môi một khối trụ xiên có đường sinh song song với vectơ CĐĐT tổng hợp trong khối điện môi, có hai cạnh đáy song song với nhau, mỗi đáy có diện tích ∆S, đường sinh có chiều dài L. - σ’ + σ’ ∆S α L Gọi n là pháp tuyến của đáy mang điện tích dương và α là góc hợp bởi và E ,-σ và σ là mật độ điện tích mặt trên mỗi đáy. Ta có thể coi toàn bộ khối trụ như một LCĐ tạo ra bởi các điện tích liên kết –σ’∆S và σ’∆S trên hai đáy nằm cách nhau một đoạn L. Momen điện của nó có độ lớn là : σ’. ∆S.L Theo định nghĩa của vectơ phân cực điện môi ta có: n pei i 1 Pe Pe V n Trong đó: p ei '. S . L và ∆V = ∆S.L. cosα là thể i 1 tích của hình trụ xiên. '. S.L ' Do đó: P e S.L.cos cos Suy ra : ' Pe cos Pen P e cos P en là hình chiếu của vectơ phân cực điện môi trên pháp tuyến n b) Liên hệ giữa vectơ phân cực điện môi và mật độ điện tích khối: lk divPe III.Vectơ điện cảm Nếu kể đến điện tích liên kết như là nguồn sinh ra trường như các điện tích tự do thì: divE lk 00 div00 E divPee div() E P D 0 E P e được gọi là vectơ điện cảm Vậy: div D Nhân hai vế phương trình trên với dV rồi lấy tích phân theo thể tích V bất kỳ ta được: divDdV dV Dd S Q VVS Đây là ĐL Gauss trong điện môi Nếu chất điện môi đồng chất và đẳng hướng thì D 0 E e0 E 0(1 e )E 0 E 1 e gọi là hằng số điện môi IV. Điều kiện biên: Ta vẽ một mặt trụ dS 2 D2 chiều cao vô cùng bé ở gần mặt phân cách giữa hai hai chất điện ∆S môi 1 và 2. Áp dụng định lý Gauss D1 Dd S 0 D S D S 0 2n 1n S d S1 D2n D1n 2E2n 1E1n * Thành phần pháp tuyến của vectơ cảm ứng điện biến thiên liên tục khi đi qua mặt phân cách của hai lớp điện môi. * Thành phần pháp tuyến của vectơ cường độ điện trường biến thiên không liên tục khi đi qua mặt phân cách của hai lớp điện môi. Ta vẽ một đường cong kín ABCDA ở gần mặt phân cách giữa hai chất điện môi 1 và 2. Ta có: Ed s 00 E21tt s E s E 1 E ABCDA 2 DD A B EE 21tt 21tt D C 21 * Thành phần tiếp tuyến của vectơ cảm ứng điện biến thiên không liên tục khi đi qua mặt phân cách của hai lớp điện môi. * Thành phần tiếp tuyến của vectơ cường độ điện trường biến thiên liên tục khi đi qua mặt phân cách của hai lớp điện môi. Câu 1: Cho tụ điện như hình vẽ 1. NLĐT trong nữa trên và nữa dưới của tụ điện phẳng: -q A. W = W +q 1 2 S/2 B. ε W = ε W2 1 1 2 S/2 C. ε2 W1 = ε1W2 D. (ε2 – 1)W1 = (ε1 – 1) W2 2. CĐĐT trong nữa trên và nữa dưới của tụ điện phẳng A. E1 = E2 B. ε1 E1 = ε2 E2 C. ε1 E2 = ε2 E1 D. (ε1 – 1)E2 = (ε2 – 1) E2 3. Độ cảm ứng điện trong nữa trên và nữa dưới của tụ điện phẳng A. D1 = D2 B. ε1D1 = ε2D2 C. ε1 D2 = ε2 D1 D. (ε2 – 1 )D1 = (ε1 – 1)E1 • Giải a) 11 WEE 22 ; 122o 1 1 o 1 1 t 1122 WEE2 o 2 2 o 2 2 t 22 W11 EEWW1tt 2 1 1 2 2 W22 b) EEEE1 1tt; 2 2 EEEE1tt 2 1 2 c) DD12ttDD12 2DD 1 1 2 1 2 1 2 Câu 2: Cho tụ điện như hình vẽ 1. Hiệu điện thế giữa bề mặt nữa trái và bề mặt nữa phải của tụ điện phẳng A. U1 = U2 B. ε1 U1 = ε2 U2 C. ε1 U2 = ε2 U1 D. Tất cả đều sai 2. Năng lượng điện trường ở nữa trái và nữa phải của tụ điện phẳng: +q -q A. W1 = W2 S S B. ε1W1 = ε2W2 d/2 d/2 C. ε2 W1 = ε1W2 D. (ε2 – 1)W1 = (ε1 – 1) W2 • 3. CĐĐT ở nữa trái và nữa phải của tụ điện phẳng A. E1 = E2 B. ε1 E1 = ε2 E2 C. ε1 E2 = ε2 E1 D. (ε1 – 1)E2 = (ε2 – 1) E2 • Giải a) dd UEUE1 1nn; 2 2 22 U ED 12 1nn 2 1 UED 2 2nn 1 2 1 1UU 1 2 2 b) 11 WEWE 22; 122o 1 1 n 2 o 2 2 n 22 W1 1ED 1nn 2 1 22 WED2 2 2nn 1 2 DDWW1nn 1 1 1 2 2 • c) DDEE1n 1 n 1 1 n 2 2 n EEEE1 1nn; 2 2 1EE 1 2 2 • Cho hai mặt phẳng kim loại song song tích điện đều, cách nhau một đoạn D, lần lượt có mật độ điện mặt là σA và σB . Hằng số điện môi của một lớp điện môi có bề dày d giữa chúng là ε. Xác định hiệu điện thế giữa hai mặt. d • Ta có: U E0 (). D d E d AB E0 2 0 E E 0 AB 2 0 U ABAB() D d d 2200 d AB()Dd 20 • Có hai mặt phẳng song song vô hạn mang điện trái dấu, mật độ điện mặt là +σ và –σ. Người ta lấp đầy giữa hai mặt phẳng một lớp thuỷ tinh dày 3mm (ε = 7). Hiệu điện thế giữa hai mặt phẳng trên là 1000V. Xác định mật độ liên kết ở trên mặt chất điện môi. lk P. n P 0 E U ( 1) 1,77.10 52Cm / 0 d • Khoảng không gian giữa hai bản tụ điện phẳng được lấp đầy bằng hai lớp điện môi có bề dày và hằng số điện môi lần lượt là d1 , d2 và ε1 , ε2 . Tụ điện được tích điện đến hiệu điện thế U. Tìm cường độ điện trường E1 , E2 trong các lớp điện môi và điện trường E0 trong khe hở giữa các bản tụ và các lớp điện môi. EE00 EE12 ; 12 dd12 U E1 d 1 E 2 d 2 E 0 12 U12 E0 dd1 2 2 1 UU21 EE12 ; d1 2 d 2 1 d 1 2 d 2 1
File đính kèm:
 bai_giang_vat_ly_dai_cuong_1_chuong_8_dien_moi.pdf
bai_giang_vat_ly_dai_cuong_1_chuong_8_dien_moi.pdf

