Bài giảng Vật lý đại cương 1 - Chương 7: Vật dẫn
Vật dẫn là vật có chứa các hạt
mang điện tự do; các hạt mang điện
này có thể chuyển động trong toàn
bộ vật dẫn. Có nhiều loại vật dẫn (
rắn, lỏng, khí); trong chương này ta
chỉ nghiên cứu vật dẫn kim loại.
Trong vật dẫn kim loại các hạt
mang điện tự do là các electron.I.Vật dẫn cân bằng tĩnh điện
1. Định nghĩa: Vật dẫn cân bằng tĩnh điện là
vật dẫn mà trong đó các điện tích đã nằm
cân bằng (nghĩa là không chuyển động có
hướng để tạo thành dòng điện)
2. Điều kiện cân bằng tĩnh điện
a) Vectơ CĐĐT bên trong vật dẫn bằng
không.
b) Tại mọi điểm trên bề mặt vật dẫn, vectơ
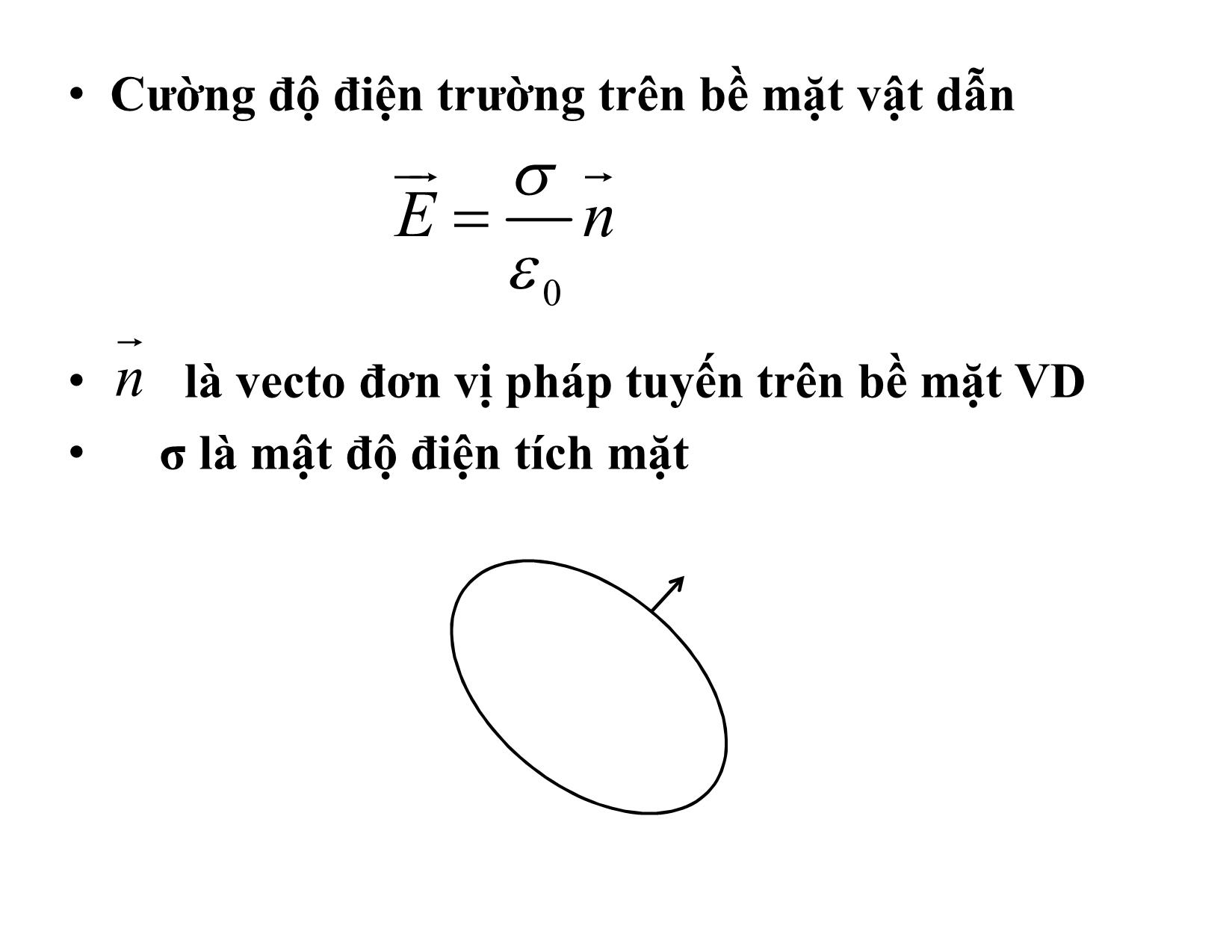
CĐĐT phải vuông góc với bề mặt vật dẫn.• Cường độ điện trường trên bề mặt vật dẫn
• là vecto đơn vị pháp tuyến trên bề mặt VD
• σ là mật độ điện tích mặt

Trang 1

Trang 2

Trang 3
Trang 4

Trang 5

Trang 6
Trang 7

Trang 8

Trang 9

Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Vật lý đại cương 1 - Chương 7: Vật dẫn

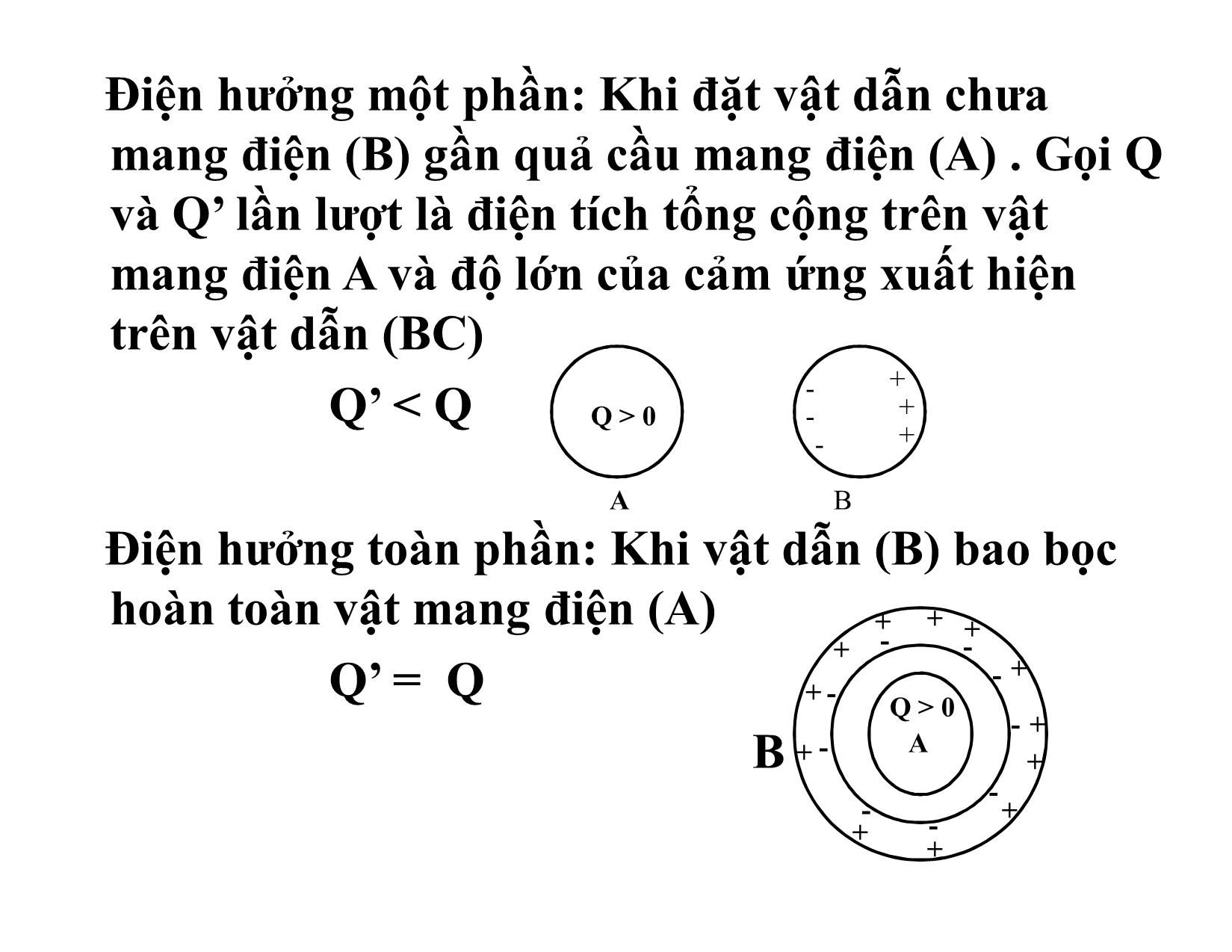
Chương VII VẬT DẪN Vật dẫn là vật có chứa các hạt mang điện tự do; các hạt mang điện này có thể chuyển động trong toàn bộ vật dẫn. Có nhiều loại vật dẫn ( rắn, lỏng, khí); trong chương này ta chỉ nghiên cứu vật dẫn kim loại. Trong vật dẫn kim loại các hạt mang điện tự do là các electron. I.Vật dẫn cân bằng tĩnh điện 1. Định nghĩa: Vật dẫn cân bằng tĩnh điện là vật dẫn mà trong đó các điện tích đã nằm cân bằng (nghĩa là không chuyển động có hướng để tạo thành dòng điện) 2. Điều kiện cân bằng tĩnh điện a) Vectơ CĐĐT bên trong vật dẫn bằng không. b) Tại mọi điểm trên bề mặt vật dẫn, vectơ CĐĐT phải vuông góc với bề mặt vật dẫn. • Cường độ điện trường trên bề mặt vật dẫn E n 0 • n là vecto đơn vị pháp tuyến trên bề mặt VD • σ là mật độ điện tích mặt 3. Tính chất a) Vật dẫn là một khối đẳng thế. b) Điện tích chỉ phân bố trên bề mặt vật dẫn; bên trong vật dẫn, điện tích bằng không (các điện tích dương và âm trung hòa lẫn nhau) c) Sư phân bố điện tích trên mặt vật dẫn chỉ phụ thuộc vào hình dạng của mặt đó, những chỗ lồi điện tích tập trung nhiều. • II. Hiện tượng điện hưởng Khi đặt một vật dẫn trung hoà điện vào trong điện trường ngoài thì dưới tác dụng của lực điện trường các electron trong vật dẫn sẽ chuyển dời có hướng ngược chiều điện trường. Kết quả là trên các mặt giới hạn của vật dẫn xuất hiện các điện tích trái dấu, mặt có đường sức điện trường ngoài đi vào mang điện dương, mặt đối diện mang điện âm và chúng có độ lớn bằng nhau. Các điện tích này gọi là điện tích cảm ứng và hiện tượng này gọi là hiện tượng điện hưởng. Điện hưởng một phần: Khi đặt vật dẫn chưa mang điện (B) gần quả cầu mang điện (A) . Gọi Q và Q’ lần lượt là điện tích tổng cộng trên vật mang điện A và độ lớn của cảm ứng xuất hiện trên vật dẫn (BC) - + Q’ 0 - + - + A B Điện hưởng toàn phần: Khi vật dẫn (B) bao bọc hoàn toàn vật mang điện (A) + + + + - - - + Q’ = Q + - Q > 0 Q > 0 - + - A B + + - - + + - + III. Điện dung của vật dẫn cô lập Vật dẫn cô lập: một vật dẫn được gọi là cô lập về điện nếu gần nó không có một vật nào khác có thể gây ảnh hưởng đến sư phân bố điện tích của nó. Điện dung của vật dẫn cô lập: Q C V V và Q là điện thế và điện tích của vật dẫn đó C là điện dung của vật dẫn, nó phụ thuộc vào hình dạng kích thước và tính chất của môi trường cách điện bao quanh nó. IV. Tụ điện 1. Định nghĩa: Tụ điện là một hệ hai vật dẫn đặt gần nhau hoặc bao bọc hoàn toàn nhau sao cho giữa chúng xảy ra hiện tượng điện hưởng toàn phần. Hai vật dẫn gọi là hai bản tụ 2. Điện dung của tụ điện Gọi V1 là điện thế của bản tích điện dương Q, V2 là điện thế của bản tích điện âm –Q Điện dung của tụ điện : Q Q C V1 V2 U U = V1 – V2 là hiệu điện thế giữa bản tích điện dương và âm V.Tính điện dung của tụ điện 1. Tụ điện phẳng: Tụ điện phẳng gồm hai tấm kim loại phẳng có hình dạng và kích thước như nhau, đặt song song đối diện nhau và cách nhau một khoảng rất nhỏ so với kích thước của chúng. S V1 d V2 -Q • Vì khoảng cách giữa hai bản rất nhỏ so với kích thước của mỗi bản nên điện trường trong khoảng không gian giữa hai bản có thể coi là điện trường do hai mặt phẳng song song vô hạn, tích điện đều bằng nhau nhưng trái dấu gây ra. + + + + + S+ + + + + + + V1 E E E d E E E - - - - - - - - - - - - - - - V2 -Q 20 20 0 • Hiệu điện thế giữa hai bản tụ : Qd U V1 V2 Ed 0S Q S C 0 • Điện dung của tụ điện phẳng: U d 2.Tụ điện cầu: Trong tụ điện cầu, hai bản tụ là hai mặt cầu đồng tâm bán kính R1 và R2 . Theo trên hiệu điện thế giữa hai bản tụ bằng: kQ 1 1 kQ(R R ) 2 1 V1 V2 R1 R2 R1R2 Do đó điện dung của tụ điện cầu là: Q R R C 1 2 V1 V 2 k ( R 2 R1 ) V. Năng lượng điện trường 1. Năng lượng tương tác của một hệ điện tích điểm Trường hợp hệ điện tích điểm gồm hai điện tích điểm q1 và q2,cách nhau một khoảng r, thế năng của điện tích q2 đặt trong điện trường của điện tích q là: 1 kq q 1 kq 1 kq W 1 2 q 2 q 1 r 2 1 r 2 2 r 1 W q V q V 2 1 1 2 2 kq2 V là điện thế do q2 gây ra tại vị trí của q1 1 r kq V 1 1 r là điện thế do q1 gây ra tại vị trí của q2 Rõ ràng W cũng là thế năng của q1 trong điện trường của điện tích q2. Nên W là thế năng tương tác hay năng lượng tương tác của hệ hai điện tích q1 và q2. Tổng quát, năng lượng tương tác điện (gọi tắt là năng lượng điện) của hệ n điện tích điểm q1,q2,qn là: 1 n W qiVi 2 i 1 Vi là điện thế tại vị trí của qi do các điện tích còn lại gây ra. • Trường hợp điện tích phân bố liên tục 1 W dq.V 2 • V là điện thế của phần tử mang điện tích dq 2. Năng lượng điện của vật dẫn cô lập tích điện Chia vật dẫn thành các phần tử VCB mang điện tích dq, năng lượng điện của vật dẫn: 1 1 1 W Vdq V dq qV 2 2 2 3. Năng lượng tụ điện 1 1 W q V ( q) V q(V V ) 2 1 2 2 1 2 Hay: 1 1 q2 1 W qU CU 2 2 2 C 2 4.Năng lượng điện trường Mật độ năng lượng điện trường là năng lượng điện trường trong một đơn vị thể tích của không gian có điện trường. Xét tụ điện phẳng, theo trên ta có: 1 1 1 W qU SEd E 2 2 2 2 0 W 1 1 E 2 E.D e 2 0 2 Kết quả này cũng đúng cho điện trường bất kỳ. Do đó năng lượng điện trường định xứ trong một thể tích τ là: W w d e Ví dụ: 1) Cho hai mặt cầu kim loại đồng tâm bán kính R1 = 4cm, R2 = 2cm mang -9 -9 điện tích Q1 = -(2/3).10 C, Q2 = 3.10 C. Tính CĐĐT và điện thế tại những điểm cách tâm mặt cầu những khoảng cách 1cm, 2cm, 3cm, 4cm. Ta có: E E1 E 2 ; V V1 V2 a) Tại r = 1cm E1 0, E2 0 E 0 kQ kQ V 1 2 R1 R2 9 2 9 9.10 ( .10 ) 9 9 9.10 (3.10 ) 3 4.10 2 2.10 2 1200V b) r = 2cm kQ E 0; E 2 1 2 (2.10 2 )2 9.109.3.10 9 67,5.104V / m 4.10 4 E 67,5.104V / m kQ1 kQ2 V V1 R1 R2 9 2 9 9.10 ( .10 ) 9 9 9.10 (3.10 ) 3 1200V 4.10 2 2.10 2 c) r = 3cm E1 0; kQ 9.109.3.10 9 E 2 3.104V / m 2 (3.10 2 )2 9.10 4 E 3.104V / m kQ kQ V 1 2 R1 r 9 2 9 9.10 .( .10 ) 9 9 9.10 .(3.10 ) 3 750V 4.10 2 3.10 2 d) r = 4cm 9 2 9 k Q 9.10 .( .10 ) E 1 3 3750V / m 1 2 2 2 R1 (4.10 ) 9 9 kQ2 9.10 .310 E2 10625V / m r 2 (4.10 2 )2 Vì E 1 và E 2 ngược chiều nhau nên E cùng chiều với E 2 (hướng xa tâm) và có độ lớn E = E2 – E1 = 4375V/m 9 2 9 9.10 ( .10 ) 9 9 kQ1 kQ2 3 9.10 (3.10 ) V 2 2 525V R1 r 4.10 4.10 2) Cho ba điện tích điểm -8 -8 q1 = -4.10 C ; q2 = 5.10 C; -8 q3 = 3.10 C lần lượt đặt tại 3 đỉnh A, B, C của một hình chữ nhật ABCD cạnh AB = 3cm; BC = 4cm. Tính năng lượng tương tác của hệ 3 điện tích này. 1 W (q V q V q V ) 2 1 A 2 B 3 C kq kq 9.109.5.10 8 9.109.3.10 8 V 2 3 A AB AC 3.10 2 5.10 2 kq kq 9.109.( 4).10 8 9.109.3.10 8 V 1 3 B AB BC 3.10 2 4.10 2 kq kq 9.109.( 4).10 8 9.109.5.10 8 V 1 2 C AC BC 5.10 2 4.10 2 W 3)Hai đoạn dây thẳng, mảnh giống nhau, mỗi đoạn có chiều dài 2L được tích điện đều với mật độ điện dài λ. Người ta đặt hai đoạn dây cùng nằm trên một đường thẳng, khoảng cách giữa hai đầu gần nhất bằng a. Tìm thế năng tương tác của hai đoạn dây này trong chân không. 2L x a Điện thế do đoạn dây 1 gây ra tại điểm M có tọa độ x: 2L x V k ln x Thế năng tương tác giữa đoạn dây thứ nhất và phầntử mang điện tích d x của đoạn dây thứ hai: 2L x dW (dx)V k2 ln dx x a 2L a 2L W k2 ln(2L x)dx k2 lnxdx a a 2 k a 4L ln(a 4L) 2(a 2L)ln(a 2L) alna 4) Hai quả cầu kim loại bán kính lần lượt là R1 và R2 với R2 = 2R1 đặt rất xa nhau, được nối với nhau bằng sợi dây dẫn mảnh được tích điện tổng cộng là Q = 9.10-8C. Tính điện tích trên mỗi quả cầu. Sau khi nối điện thế hai quả cầu bằng nhau nên: kQ' kQ' kQ' kQ' 1 2 1 2 R1 R2 R1 R2 k(Q' Q' ) k(Q Q ) kQ 1 2 1 2 R1 R2 R1 R2 R1 R2 ' R1Q 8 Q1 6.10 C R1 R2 ' R2Q 8 Q2 3.10 C R1 R2 5)Hai quả cầu kim loại tích điện, tiếp xúc với nhau và cân bằng điện. Bán kính và điện tích của chúng lần lượt là R1; q1 và R2 và q2. Nếu R2 = 2R1, so sánh điện tích của hai quả cầu. Điện thế của hai quả cầu: kq1 kq2 kq2 kq1 V1 ; V2 R1 R1 R2 R2 R1 R2 Mà: V1 = V2 nên: kq kq kq kq 1 2 2 1 R1 R1 R2 R2 R1 R2 kq kq kq kq 1 2 2 1 R1 3R1 2R1 3R1 q2 4q1 6) Một quả cầu bán kính R mang điện tích Q phân bố đều với mật độ điện tích khối ρ. Tính: a) Năng lượng điện trường bên trong quả cầu b) Năng lượng điện trường bên ngoài quả cầu c) Năng lượng điện trường trong toàn không gian Áp dụng công thức: 1 W E 2d ; d 4 r 2dr 2 0 r a) Bên trong quả cầu: E 30 1 R 2r 2 4 2 R5 W 4 r 2dr in 0 2 2 0 9 0 90 0 4 3Q Q R3 3 4 R3 1 Q2 W k in 10 R b) Bên ngoài quả cầu Q E k r 2 1 k 2Q2 1 Q2 W 4 r 2dr k ext 0 4 2 R r 2 R c) 3 Q2 W W W k in ext 5 R
File đính kèm:
 bai_giang_vat_ly_dai_cuong_chuong_7_vat_dan.pdf
bai_giang_vat_ly_dai_cuong_chuong_7_vat_dan.pdf

