Bài giảng Vật lý đại cương 1 - Chương 3: Động lực học hệ chất điểm
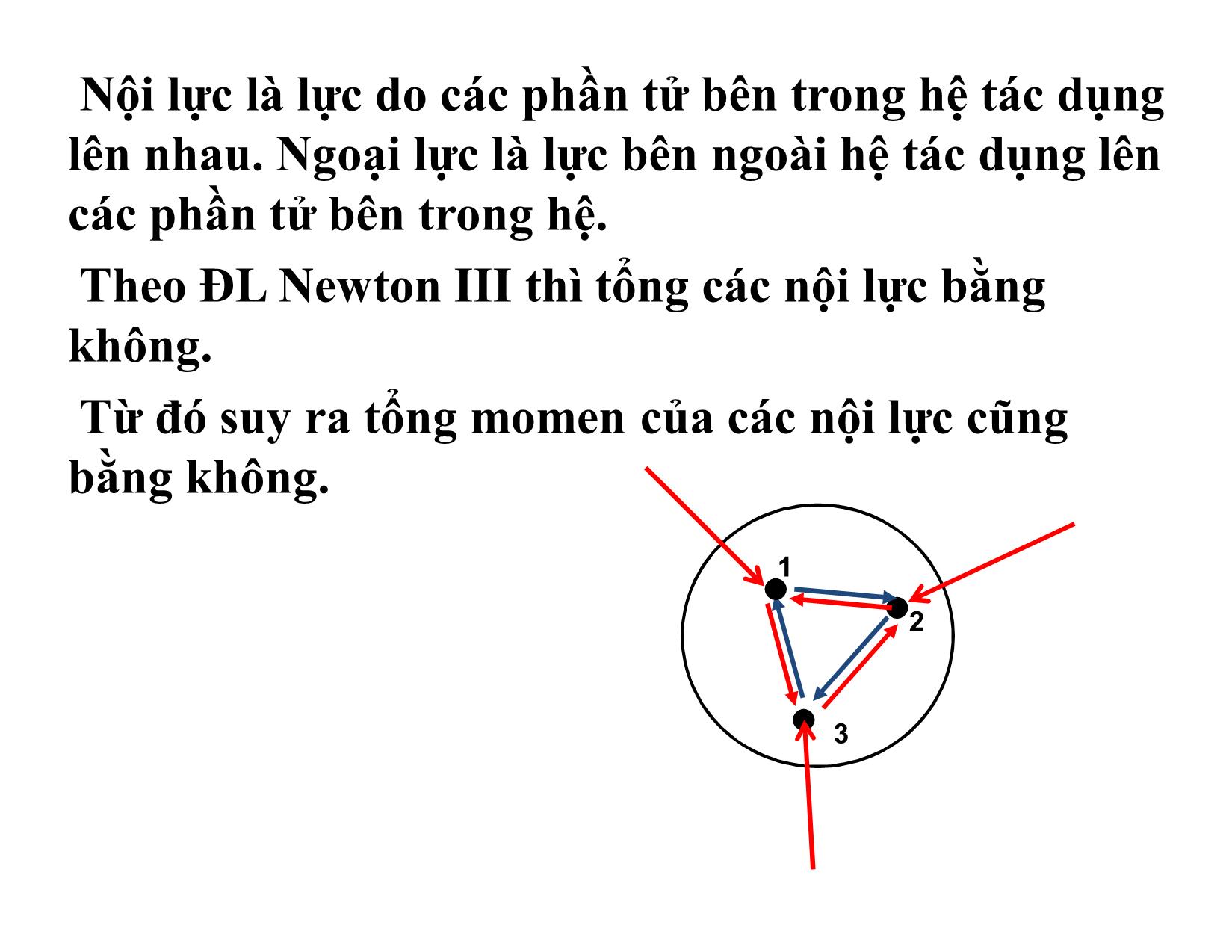
Nội lực là lực do các phần tử bên trong hệ tác dụng
lên nhau. Ngoại lực là lực bên ngoài hệ tác dụng lên
các phần tử bên trong hệ.
Theo ĐL Newton III thì tổng các nội lực bằng
không.
Từ đó suy ra tổng momen của các nội lực cũng
bằng không
Nếu nhưng hình chiếu của lên một
phương nào đó bằng không thì động lượng được
bảo toàn theo phương đó .
Ví dụ: Fx = 0 thì Px = const
Ví dụ: Một khẩu đại bác không có bộ phận
chống giật, nhả đạn dưới một góc α = 45o so với
mặt phẳng nằm ngang. Viên đạn có khối lượng m
= 10kg và có vận tốc ban đầu vo = 200m/s. Đại
bác có khối lượng M = 500kg. Hỏi vận tốc giật lùi
của súng nếu bỏ qua ma sát

Trang 1
Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7

Trang 8
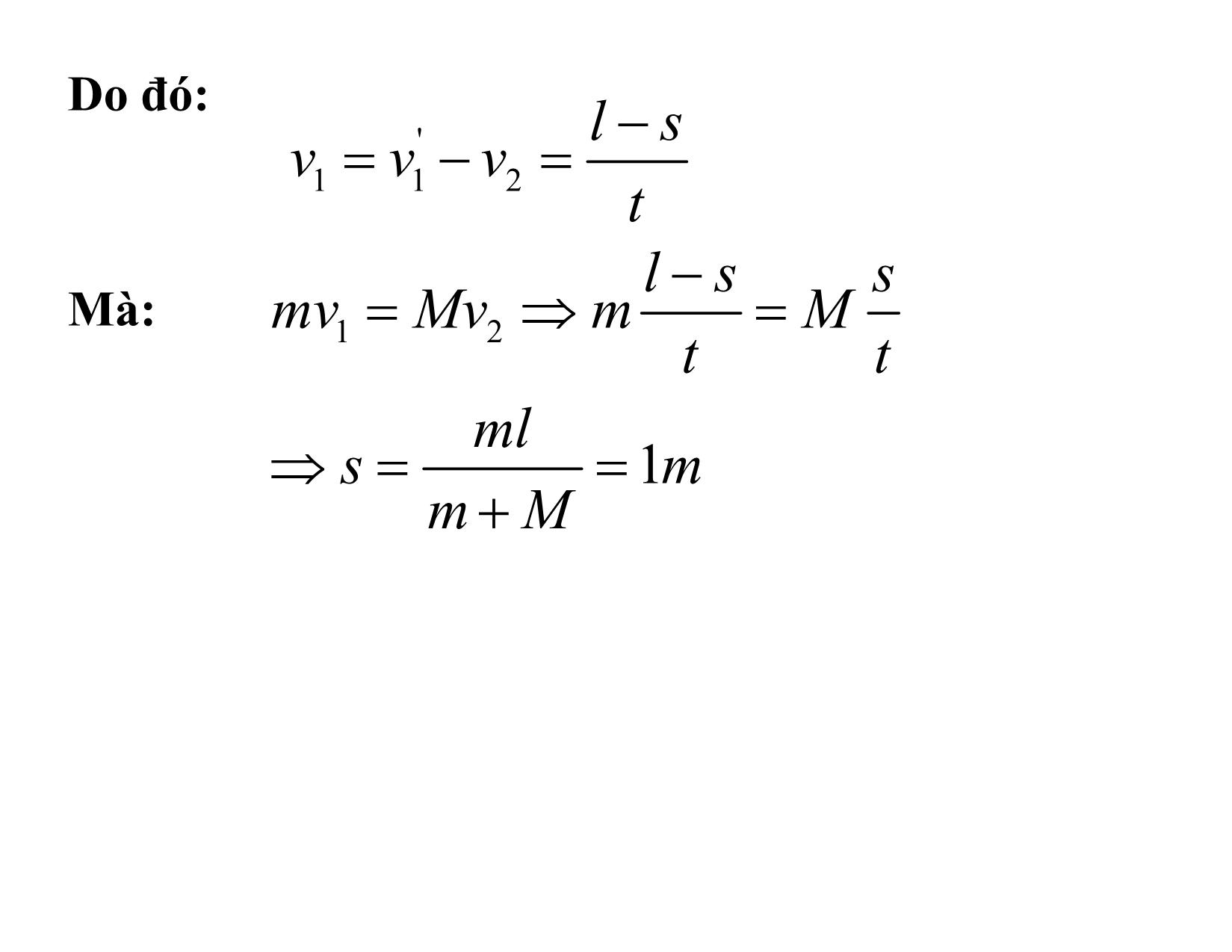
Trang 9

Trang 10
Tải về để xem bản đầy đủ
Bạn đang xem 10 trang mẫu của tài liệu "Bài giảng Vật lý đại cương 1 - Chương 3: Động lực học hệ chất điểm", để tải tài liệu gốc về máy hãy click vào nút Download ở trên
Tóm tắt nội dung tài liệu: Bài giảng Vật lý đại cương 1 - Chương 3: Động lực học hệ chất điểm

Chương III ĐỘNG LỰC HỌC HỆ CHẤT ĐiỂM Nội lực là lực do các phần tử bên trong hệ tác dụng lên nhau. Ngoại lực là lực bên ngoài hệ tác dụng lên các phần tử bên trong hệ. Theo ĐL Newton III thì tổng các nội lực bằng không. Từ đó suy ra tổng momen của các nội lực cũng bằng không. 1 2 3 I. Động lượng hệ chất điểm 1. Định nghĩa: P pi mi vi i i 2. Định lý và định luật ĐLHCĐ , a) dP d pi d pi ; Fi Fi dt i dt dt Fi là tổng các ngoại lực tác dụng vào chất điểm i F’i là tổng các nội lực tác dụng vào chất điểm i d P , Fi Fi Fi F dt i i i • Vậy: d P F dt là tổng các ngoại lực tác dụng vào HCĐ F Fi i b) p2 t2 t2 d P Fdt P2 P1 Fdt p1 t1 t1 c) Nếu F 0 p const d) Nếu F 0 nhưng hình chiếu của F lên một phương nào đó bằng không thì động lượng được bảo toàn theo phương đó . Ví dụ: Fx = 0 thì Px = const Ví dụ: Một khẩu đại bác không có bộ phận chống giật, nhả đạn dưới một góc α = 45o so với mặt phẳng nằm ngang. Viên đạn có khối lượng m = 10kg và có vận tốc ban đầu vo = 200m/s. Đại bác có khối lượng M = 500kg. Hỏi vận tốc giật lùi của súng nếu bỏ qua ma sát Giải: Ngoại lực tác dụng lên hệ gồm trọng lực và phản lực của mặt đường có phương thẳng đứng. Nên hình chiếu của chúng lên phương ngang bằng không Áp dụng ĐLBTĐL theo phương ngang cho hệ gồm súng và đạn mv cos MV 0 mv cos V 3,5m / s M Một người có khối lượng m = 60kg đứng trên một con thuyền dài 3m có khối lượng M = 120kg, đang đứng yên trên mặt nước yên lặng. Người đó bắt đầu đi từ mũi thuyền đến chỗ lái thuyền (đuôi thuyền). Hỏi khi người đó đi tới chỗ lái thuyền thì thuyền đã đi được một đoạn bao nhiêu? Bỏ qua sức cản của nước. Áp dụng ĐLBTĐL cho hệ người và thuyền: m 0 mv1 M v2 v2 v1 M v 1 là vận tốc của người đối với bờ v 2 là vận tốc của thuyền đối với bờ Gọi v ' là vận tốc của người so với thuyền thì: 1 ' ' v1 v1 v2 v1 v1 v2 Ta có: l s v' ;v 1 t 2 t l là chiều dài thuyền, s là đoạn đường thuyền đi được trong thời gian t. Do đó: l s v v' v 1 1 2 t l s s Mà: mv Mv m M 1 2 t t ml s 1m m M II. Khối tâm 1.Định nghĩa: Khối tâm G của hệ chất điểm là vị trí thỏa mãn hệ thức: mi M iG 0 i Mi là vị trí chất điểm i 2. Vị trí khối tâm : đối với điểm O trong HQC nào đó được xác định bởi vectơ vị trí rG OG Ta có: OG OM i M iG mi OG mi OM i mi M iG i i i mi OM i OG i mi i mi ri r OM ; M m r với i i i G M i Tọa độ khối tâm trong hệ tọa độ Descartes: mi xi mi yi mi zi x i ; y i ; z i G M G M G M Khối tâm của vật rắn: chia VR ra làm các phần tử khối lượng dm VCB coi như chất điểm: dm.x dm.y dm.z x ; y ; z G M G M G M x, y, z là tọa độ của phần tử khối lượng dm Lưu ý: * Với các vật đồng chất mà dạng hình học có yếu tố đối xứng thì khối tâm nằm trên các yếu tố đó. * Trong trọng trường khối tâm trùng với trọng tâm, tuy nhiên khái niêm khối tâm có ý nghĩa cơ bản hơn trọng tâm bởi vì trong tình trạng không trọng lực trọng tâm không còn nhưng khối tâm vẫn có. * Trong trọng trường đồng nhất có gia tốc g thế năng của VR bằng thế năng của khối tâm mang tổng khối lượng. Nếu hệ S gồm hai hệ S1 và S2 thì: m OG m OG OG 1 1 2 2 m1 m2 • G, G1, G2 là khối tâm của S, S1, S2 • m1, m2 là khối lượng của S1, S2 3) Vận tốc khối tâm dri mi dr dt v G i G dt M mi vi pi P i i M M M 4) Gia tốc khối tâm: dv 1 d P F a G G dt M dt M 5) Phương trình chuyển động của khối tâm F MaG Vậy khối tâm của hệ chuyển động như một chất điểm có khối lượng bằng tổng khối lượng của hệ và chịu tác dụng của một lực bằng tổng các ngoại lực tác dụng lên hệ đặt tại khối tâm. 6) Nếu F 0 thì : aG 0 vG const Khối tâm của hệ hoặc đứng yên hoặc chuyển động thẳng đều Ví dụ 1: Tại ba đỉnh của một tam giác đều cạnh a có đặt ba chất điểm, khối lượng lần lượt bằng m1, m2, m3. Xác định khối tâm của hệ ba chất điểm đó. Chọn hệ trục tọa độ Oxy như hình vẽ, ta có: m1x1 m2x2 m3x3 xG m1 m2 m3 y a m 0 m2 m3a ● 2 2 m m m x 1 2 3 O ● ● m1 m3 m1y1 m2 y2 m3 y3 yG m1 m2 m3 a 3 0 m2 0 2 m1 m2 m3 Ví dụ 2: Xác định vị trí khối tâm của một sợi dây đồng chất, khối lượng m được uốn thành một cung tròn AB tâm O bán kính R với góc mở AÔB = 2αo Vì sợi dây đối xứng qua đường phân giác của góc AÔB nên khối tâm của nó nằm trên đường phân giác này. Chọn trục Ox trùng với đường phân giác. Tọa độ khối tâm: 1 x dm.x G m A R m m dα α x dm dl .R.d O l R.2 o x Rcos B R o R xG cos d sin o 2 o o o Ví dụ 3: Xác định vị trí khối tâm của một hình quạt đồng chất, khối lượng m, bán kính R với góc mở AÔB = 2αo dS rdrd rd dr d r Vì hình quạt đối xứng qua đường phân giác của góc AÔB nên khối tâm của nó nằm trên đường phân giác này. Chọn trụ ... óc với mặt phẳng của đĩa. 1) I dm.R 2 R 2 dm I mR 2 2) m I dm.r2 ; dm rdrd R2 m R 2 I r3dr d 2 R 0 0 1 I mR2 2 Ví dụ : Xác định mômen quán tính của: 1) Một vành tròn đồng chất khối lượng m, bán kính R đối với trục đi qua tâm và nằm trong mặt phẳng của vành. 2) Một đĩa tròn đồng chất khối lượng m, bán kính R đối với trục đi qua tâm và nằm trong mặt phẳng của đĩa. a) dI dm.(Rsin )2 m Rd .R2 sin2 α 2 R mR2 sin2 d 2 mR2 2 1 I dI sin2 d mR2 2 0 2 b) Chia đĩa thành các vành tròn bán kính r bề dày dr, khối lượng của nó là: m 2mrdr dm 2 rdr R2 R2 1 mr3dr dI dmr 2 2 R2 m R 1 I dI r3dr mR2 2 R 0 4 3)Một đĩa bằng đồng khối lượng riêng ρ có bề dày b, bán kính R. Đĩa bị khoét thủng hai lỗ tròn O bán kính R/2 như hình vẽ. Tìm mômen quán tính của đĩa đã bị khoét đối với trục vuông góc với đĩa và đi qua tâm O của đĩa Ta có: I Io (I1 I2) Io, I1, I2 lần lượt là MMQT của đĩa khi chưa bị khoét và mỗi phần khoét đối với trục vuông góc với đĩa và đi qua tâm O của đĩa. Ta có: Với 1 I m R2 o 2 o 2 2 1 R R I1 I2 m1 m1 2 2 2 2 mo b R 2 R 5 bR4 m1 b I 2 16 4) Tìm mômen quán tính của bản mỏng đồng chất hình chữ nhật khối lượng m, các cạnh là a và b đối với trục vuông góc với mặt bản và đi qua một đỉnh của bản. 1 dI dm .b 2 dm .x 2 12 m m dm bdx dx ab a Momen QT đối với trục đi qua khối tâm và thẳng góc với mặt bảng a a 2 1 m 2 m I dI b2dx x2dx o a 12 a a a 2 2 1 m a2 b2 12 MMQT đối với trục đi qua một đỉnh của bảng và thẳng góc với mặt bảng. Áp dụng ĐL Steiner – Huyghen a2 b2 1 I I m m a2 b2 o 4 4 3 V. Chuyển động của Vật Rắn: 1) Chuyển động tịnh tiến: Vật rắn chuyển động tịnh tiến khi vectơ nối hai điểm M,N bất kỳ của nó không đổi trong quá trình chuyển động M N M N M N MN c ON OM c Lấy đạo hàm hai vế, ta suy ra VN VM ; aM aN Vậy các chất điểm của VR đều có cùng vectơ vận tốc và gia tốc. Do đó để xác định chuyển động tịnh tiến của VR, ta chỉ cần xác định chuyển động của một điểm trên VR, thường chọn khối tâm. Chú ý: Trong chuyển động tịnh tiến QĐ của các chất điểm của vật rắn có thể là các đường cong Phương trình chuyển động tịnh tiến của VR F M a M là khối luợng của VR F là tổng các ngoại lực tác dụng vào VR 2. Chuyển động quay quanh một trục cố định VR (cố thể) chuyển động quay quanh một trục cố định nếu có hai điểm đứng yên. Mọi chất điểm nằm trên đường nối hai điểm này, gọi là trục quay của VR, cũng đứng yên. Các chất điểm không nằm trên trục quay chuyển động tròn có tâm nằm trên trục và bán kính bằng khoảng cách từ chất điểm đến trục quay. Khi VR quay quanh một trục cố định thì: * Trong cùng khoảng thời gian, mọi điểm của VR đều quay được cùng một góc θ. * Tại cùng một thời điểm, mọi điểm của VR đều có cùng: d vận tốc góc : dt d và gia tốc góc : dt a)MMĐL của HCĐ quay quanh một trục cố định: Ta đặt trục z trùng với trục quay cố định. Trên trục z ta lấy một điểm O z O ri pi mi vi MMĐL của chất đ iểm i đối với điểm O, theo ĐN là: Li ri mi vi MMĐL của HCĐ đối với điểm O: L Li i MMĐL của HCĐ đối với trục z Lz Liz i Môđun của L i là 2 Li mirivi mirii Ri miri i Iii trong đó Ri là k hoảng cách từ chất điểm i đến trục quay. Vì L nằm trên trục z nên hình chiếu i của L i lên trục z là: Liz Li Iii Vậy Lz Liz Iii i i i 0 nếu i cùng chiều với trục z và âm nếu ngược lại b)Mômen ĐL của VR quay quanh một trục cố định Khi đó mọi chất điểm của VR đều có cùng vận tốc góc nên các i đều bằng nhau và bằng nên : Lz Ii I i với I là m ômen QT của VR đối với trục quay. Vì L và cùng phương chiều nên: L I c) Tác dụng của lực trong chuyển động quay của VR quanh một trục cố định: Giả thiết có một lực tác dụng lên vật rắn, phân tích ra hai thành F phần: F F 1 F 2 , F 1 ┴ trục ; F 2 | | trục. Lực F 1 nằm trong mặt phẳng vuông ∆ góc với trục đi qua M lại được phân tích ra hai thành phần: F 2 F F F F 1 t n O Ft M F Fn 1 Trong đó F t ┴ bán kính OM nghĩa là nằm theo tiếp tuyến của vòng tròn tâm O bán kính OM còn Fn nằm theo bán kính OM. Kết quả ta có: F F t F n F 2 Ta thấy rằng : - F2 không gây ra chuyển động quay, chỉ có tác dụng làm vật rắn trượt dọc theo truc quay - Fn không gây ra chuyển động quay, chỉ có tác dụng làm vật rắn dời khỏi trục quay. Vậy trong chuyển động quay của một vật rắn xung quanh một trục chỉ những thành phần lực tiếp tuyến với quỹ đạo của điểm đặt mới có tác dụng thực sự. d) Momen của lực đối với trục quay MO(F) MO(Ft ) MO(Fn ) MO(F2) M (F) M (Ft ) M (Fn ) M (F2 ) MO(F) OM F MO(F) nằm trên trục t t t Nên: M (Ft ) OM.Ft sin(OM,Ft ) r.Ft MO(Fn) OM Fn 0 M (Fn) 0 MO(F2) OM F2 MO(F2) M (F2) 0 Vậy M (F) M (Ft ) r.Ft Momen lực là đại lượng đặc trưng cho tác dụng của lực trong chuyển động quay. Momen của lực đối với trục sẽ bằng không khi lực đó bằng không hoặc khi lực đó đồng phẳng với truc ∆. e)Phương trình cơ bản của VR quay quanh trục cố định Ta có MMĐL của VR đối với trục quay: dL d L I I I dt dt M I Đây là phương trình cơ bản của VR quay quanh trục cố định Trong đó M là tổng mômen của các ngoại lực tác dụng lên vật rắn đối với trục quay, I là momen quán tính của VR đối với trục quay. Chú ý: Mômen lực đối với trục có trị đại số Bài 1: Một đĩa tròn khối lượng m1 = 100kg quay với vận tốc góc ω1 = 10 vòng/phút. Một người khối lượng m2 = 60 kg đứng ở mép đĩa. Hỏi vận tốc góc của đĩa khi người đi vào đứng ở tâm đĩa. Áp dụng ĐLBTMMĐL đối với trục cho hệ gồm đĩa và người: I11 I22 1 2 2 1 2 m1R m2R 1 m1R 2 2 2 m1 2m2 2 1 22vòng / phút m1 Bài 2: Một thanh có chiều dài l quay xung quanh một trục nằm ngang đi qua một đầu thanh. Lúc đầu, thanh ở vị trí nằm ngang, sau đó được thả ra. Tìm gia tốc góc của thanh lúc bắt đầu thả rơi và lúc thanh đi qua vị trí thẳng đứng Phương trình chuyển động quay của thanh M I 1 2 Với I ml 3 a) Lúc bắt đầu thả rơi l 3g M mg 14,7rad / s2 2 2l b) Lúc thanh đi qua vị trí thẳng đứng M 0 0 Bài 3: Một cột đồng có chiều cao h, đang ở vị trí thẳng đứng thì bị đổ xuống. Xác định: a) Vận tốc dài của đỉnh cột khi nó chạm đất b) Vị trí của điểm M trên cột sao cho khi M chạm đất thì vận tốc của nó đúng bằng vận tốc chạm đất của một vật thả rơi tự do từ vị trí M. a) Áp dụng ĐLBTCN: E1 E2 h 1 1 1 mg I 2 mh2 2 2 2 2 3 3g h v h 3gh 12,2m / s b) Gọi x là độ cao của điểm M khi cột ở vị trí thẳng đứng Vận tốc chạm đất của vật thả rơi tự do từ vị trí M là: vM 2gx Theo đầu bài thì : 3g v x 2gx x M h 2 x h 3 3.Chuyển động song phẳng: Chuyển động song phẳng của vật thể là chuyển động trong đó tất cả các điểm đều di chuyển song song với một mặt phẳng cố định P nào đó. Ta xét tiết diện S của vật bị cắt bởi mặt phẳng Oxy nào đó song song với mặt phẳng P. Vì trong chuyển động song phẳng, tất cả các điểm của vật nằm trên đường thẳng vuông góc với mặt cắt S đều chuyển động như nhau, nên để xác định chuyển động của toàn vật thể chỉ cần nghiên cứu chuyển động của mặt cắt S của vật thể trên mặt phẳng Oxy. Giả sử mặt cắt S là tam giác với các đỉnh ban đầu ở vị trí A, B, C trong mặt phẳng Oxy, sau khoảng thời gian ∆t khá bé chúng chiếm các vị trí A’, B’, C’ cũng thuộc mặt phẳng này. Chuyển động của tam giác có thể thực hiện như sau: - Tịnh tiến tam giác từ vị trí ban đầu đến vị trí (I) sao cho A đến trùng với A’, khi đó ABC dời đến A’B”C”. -Quay tam giác ở vị trí (I) C’’ C’ C quanh trục qua A’ và B’ vuông góc với mặt phẳng A’ B’’ A B hình vẽ (Oxy) đến vị trí (II) sao cho B” đến trùng với B’, khi đó C” đến trùng với C’. Tổng quát, người ta chứng minh được rằng: Chuyển dịch bất kỳ của VR từ vị trí này đến vị trí khác trong khoảng thời gian khá bé, có thể thực hiện được nhờ chuyển động tịnh tiến, tương ứng với chuyển dịch của một điểm và sự quay quanh trục đi qua điểm ấy. Điểm được chọn để lấy sự dịch chuyển của nó làm chuyển dịch tịnh tiến gọi là điểm cực. • Xác định vân tốc của các điểm của vât rắn: Ký hiệu A là cực, vị trí của điểm M thuộc VR: OM OA AM Lấy đạo hàm theo thời gian: d (OM ) d (OA) d (AM ) dt dt dt vM vA AM Trường hợp VR có một điểm cố định thì chuyển động tức thời của VR là chuyển động quay quanh trục, trục tức thời luôn đi qua điểm cố định. • Ttrường hợp chuyển động của VR là chuyển động lăn không trượt Khi VR chuyển động lăn không trượt, mặt cắt S của VR là hình tròn thẳng góc với trục quay. Nếu chuyển động củaVR là chuyển động lăn không trượt của một vật thể ví dụ hình trụ trên bề mặt của một vật thể cố định khác thì: Điểm tiếp xúc A có vận tốc tức thời bằng 0 ( VA = 0 vì các tiếp điểm của hai vật khi không trượt lên nhau phải có cùng vận tốc, mà vật thứ hai là cố định) Trong chuyển động lăn không trượt, lực ma sát không sinh công Nếu chọn khối tâm G của VR làm điểm cực thì phương trình động lực học miêu tả chuyển động lăn không trượt của VR là: * PTCĐTT của khối tâm G : F MaG * PTCĐ quay quanh trục đi qua G M I F là tổng các ngoại lực tác dụng lên VR. M là tổng momen của các ngoại lực đối với trục I là momen quán tính của VR đối với trục Vận tốc và gia tốc khối tâm trong chuyển động lăn không trượt. • VG = Rω N • aG = Rβ ω và β là vận tốc M G và gia tốc góc của VR P A VI. Động năng của HCĐ 1.Động năng của HCĐ: 1 2 K mivi i 2 2.ĐN của VR CĐ tịnh tiến: trong chuyển động tịnh tiến vận tốc của các chất điểm đều bằng nhau nên 1 2 1 2 1 2 K miv mi v Mv i 2 2 i 2 M mi là khối lượng của VR i 3) ĐN của VR quay quanh trục cố định: 1 2 1 2 K mivi mi Ri i 2 2 1 2 2 1 2 mi Ri I 2 i 2 4) ĐN của VR lăn không trượt: 1 1 K M v 2 I 2 2 G 2 1 Mv 2 là ĐN chuyển động tịnh tiến của khối tâm 2 G 1 I 2 là ĐN chuyển động quay quanh trục qua 2 khối tâm VII. Công và công suất của VR quay quanh trục cố định Xét trường hợp một VR quay xung quanh một trục cố định dưới tác dụng của lực tiếp tuyến Ft. Công vi phân của lực tiếp tuyến là: dA = Ft .ds Trong đó ds = rdα , dα là góc quay ứng với chuyển dời ds. Vậy : dA rFt d Md dA d Công suất: P M M dt dt Tổng quát: P M. Bài 1: Trên một hình trụ đặc đồng chất có khối lượng M và bán kính R người ta quấn một sợi chỉ mảnh. Một đầu sợi chỉ có M buộc một vật có khối lượng m. Tại lúc t = 0 hệ bắt đầu chuyển động. m Bỏ qua sự ma sát ở trục hình trụ, tìm sự phụ thuộc theo thời gian của: a) Vận tốc góc của hình trụ; b) Động năng của toàn hệ. a) PT Newton 2 cho vật: mg T ma Chiếu lên phương chuyển động: mg – T = ma (1) T PT chuyển động quay của ròng rọc: T M I 1 a 1 TR MR2 T Ma (2) mg 2 R 2 Từ (1) và (2) suy ra: mg a M m 2 Vận tốc của vật tại thời điểm t: mgt v mgt v at ; M R M m R m 2 2 b) Động năng của hệ tại thời điểm t: 1 1 1 1 1 v2 W mv2 I 2 mv2 MR 2 2 2 2 2 2 R2 1 M 1 (mgt)2 m v2 2 2 2 M m 2 Bài 2: Một quả cầu đồng chất có khối lượng m và bán kính R lăn không trượt trên một mặt phẳng nghiêng tạo thành một góc α với mặt phẳng nằm ngang. Tìm: a) giá trị của hệ số ma sát sao cho sự trượt không xảy ra b) động năng của quả cầu sau t giây kể từ lúc bắt đầu chuyển động. PT chuyển động tịnh tiến của khối tâm: mg N Fms ma Chiếu lên phương chuyển động của khối tâm: mg sin Fms ma PT chuyển động quay quanh trục qua KT: M I N 2 a R.F mR2 ms 5 R Fms 2 Fms ma 5 mg 5 2 a g sin F g sin 7 ms 7 Điều kiện để vật không trượt: 2 2 F kN g sin kmg cos k tg ms 7 7 b) Động năng của vật sau t giây: 2 1 2 1 2 1 2 1 2 2 v 7 2 Wđ mv I mv mR mv 2 2 2 2 5 R2 10 5 5 v at gtsin W mg2t2 sin2 7 đ 14 Bài 3: Từ đỉnh một mặt phẳng nghiêng cao h, người ta cho một đĩa tròn lăn không trượt trên mặt phẳng nghiêng đó. Tìm vận tốc dài của đĩa ở cuối mặt phẳng nghiêng Cách 1: mg N Fms ma Chiếu lên phương chuyển động của khối tâm: mg sin Fms ma (2) PT chuyển động quay quanh trục qua KT: M I 1 a 1 RF mR2 F ma (2) ms 2 R ms 2 2 a gsin 3 2 h 4 v2 2as 2 gsin . v gh 3 sin 3 Cách 2: Áp dụng ĐLBTCN: 1 1 1 1 1 v2 mgh mv2 I2 mv2 mR2 2 2 2 2 2 R2 3 4 mv2 v gh 4 3 N Fms mg VII. Va chạm Khảo sát bài toán va chạm của hai quả cầu nhỏ chuyển động trên đường thẳng nối liền hai tâm của chúng ( va chạm xuyên tâm) Khối lượng của hai quả cầu lần lượt là m1 và m2. Tr ước va chạm chúng có vectơ vận tốc là v 1 và v2 (cùng phương). ' ' Sau va chạm, chúng có vectơ vận tốc là v 1 và v2 (cùng phương như ban đầu). Giả thiết hệ (m1 + m2) cô lập. Động lượng của hệ được bảo toàn nên m1v1 m2v2 m1v'1 m2v'2 Chiếu lên phương chuyển động ta được ' ' m1v1 m2v2 m1v1 m2v2 (1) Ta xét hai trường hợp: 1.Va chạm đàn hồi: Động năng của hệ (m1 và m2) trước và sau va chạm được bảo toàn. Do đó: 1 1 1 1 mv2 m v2 mv'2 mv'2 (2) 2 1 1 2 2 2 2 1 1 2 2 2 Giải hệ PT (1) và (2) ta được: ' (m1 m2 )v1 2m2v2 v1 m1 m2 ' (m2 m1)v2 2m1v1 v2 m1 m2 2.Va chạm mềm: Sau va chạm hai quả cầu dính ' ' vào nhau chuyển động cùng vận tốc v 1 v 2 v . Vậy (1) trở thành: m1v1 m2v2 (m1 m2 )v m v m v v 1 1 2 2 m1 m2 Trong va chạm mềm động năng không được bảo toàn mà bị giảm đi. Có một phần động năng biến thành nhiệt. Ví dụ 1: Hai quả cầu được treo ở đầu hai sợi dây song song dài bằng nhau. Hai đầu kia của các sợi dây được buộc vào một cái giá sao cho các quả cầu tiếp xúc với nhau và tâm của chúng cùng nằm trên một đường nằm ngang. Khối lượng của các quả cầu lần lượt bằng 200g và 100g. Quả cầu thứ nhất được nâng lên độ cao h = 4,5cm rồi thả xuống. Hỏi sau va chạm, các quả cầu được nâng lên độ cao bao nhiêu nếu: a) Va chạm là hoàn toàn đàn hồi; b) Va chạm là mềm. Vận tốc quả cầu 1 ngay trước va chạm: 1 m v2 mgh v 2gh 2 1 1 1 a) Va chạm là hoàn toàn đàn hồi Vận tốc của quả cầu 1 ngay sau va chạm ' (m1 m2 )v1 2m2v2 1 1 v1 v1 2gh m1 m2 3 3 Vận tốc của quả cầu 2 ngay sau va chạm ' (m2 m1) 2m1v1 4 4 v2 v1 2gh m1 m2 3 3 Áp dụng ĐLBTCN cho quả cầu 1 và 2 1 v,2 h m v,2 m gh h 1 0,5cm 2 1 1 1 1 1 2g 9 1 v,2 16h m v,2 m gh h 2 8cm 2 1 2 1 2 2 2g 9 b) Va chạm mềm: Vận tốc của (m1 + m2) ngay sau va chạm: m v 2 V 1 1 2gh m1 m2 3 Áp dụng ĐLBTCN cho m1 + m2 1 V 2 4h (m m )V 2 (m m )gH H 2cm 2 1 2 1 2 2g 9
File đính kèm:
 bai_giang_vat_ly_dai_cuong_chuong_3_dong_luc_hoc_he_chat_die.pdf
bai_giang_vat_ly_dai_cuong_chuong_3_dong_luc_hoc_he_chat_die.pdf

