Bài giảng Vật lý đại cương 1 - Chương 1: Động học chất điểm
I. Những khái niệm mở đầu
- Chuyển động của một vật là sư chuyển dời vị trí
của vật đó đối với các vật khác trong không gian và
theo thời gian
- Vật hay hệ vật được qui ước đứng yên khi khảo sát
chuyển động của các vật khác gọi là hệ qui chiếu.
Chuyển động có tính tương đối phụ thuộc HQC.
- Chất điểm là một vật có kích thước nhỏ không
đáng kể so với những khoảng cách, những kích
thước mà ta đang khảo sát
- Một tập hợp chất điểm gọi là hệ chất điểm. Vật
rắn được xem là hệ chất điểm phân bố liên tụcII.Các phương pháp mô tả chuyển động. Quỹ đạo
Để xác định chuyển động của chất điểm, cần xác
định vị trí của nó trong hệ quy chiếu đã chọn ở
mọi thời điểm. Có 3 phương pháp để xác định vị
trí của chất điểm

Trang 1

Trang 2

Trang 3

Trang 4

Trang 5

Trang 6

Trang 7
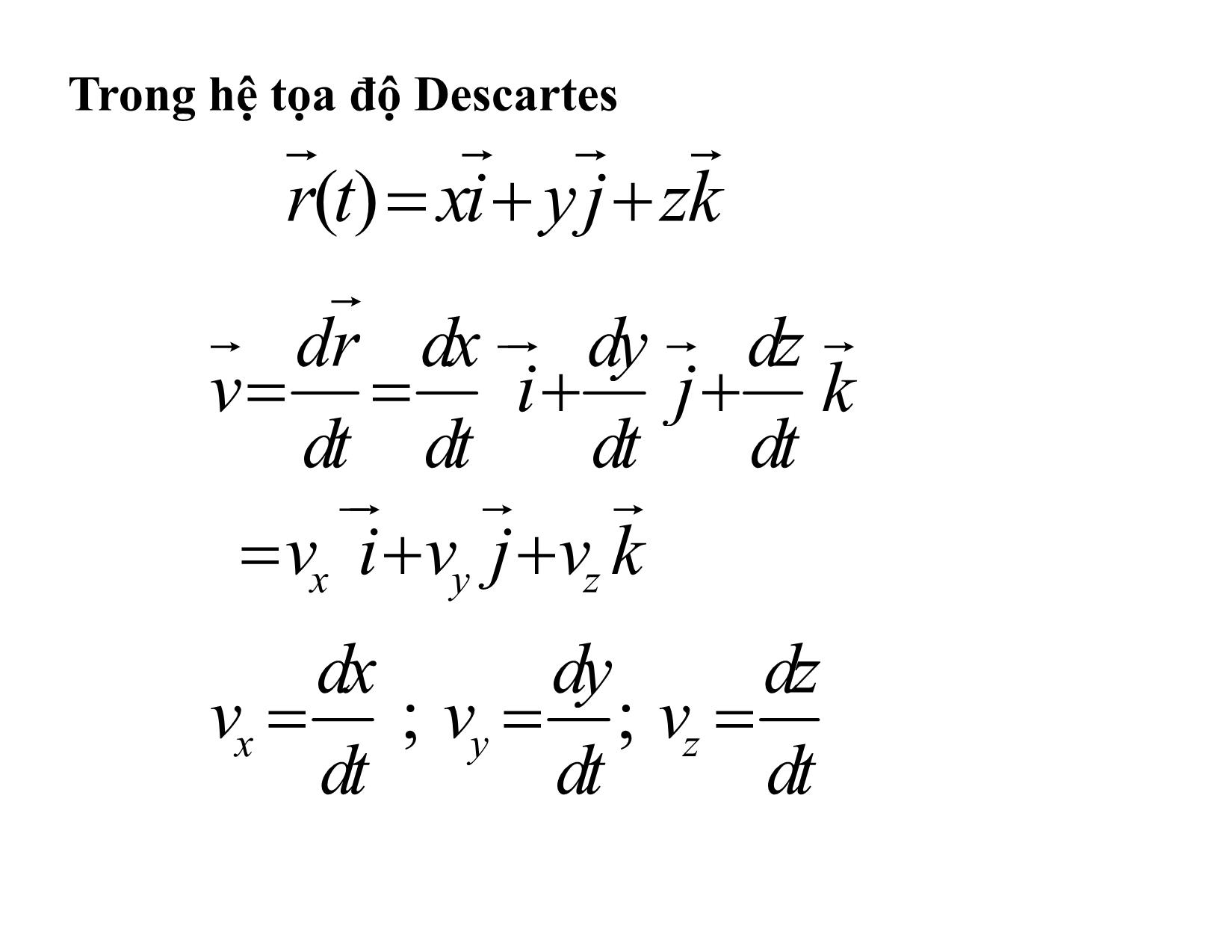
Trang 8

Trang 9
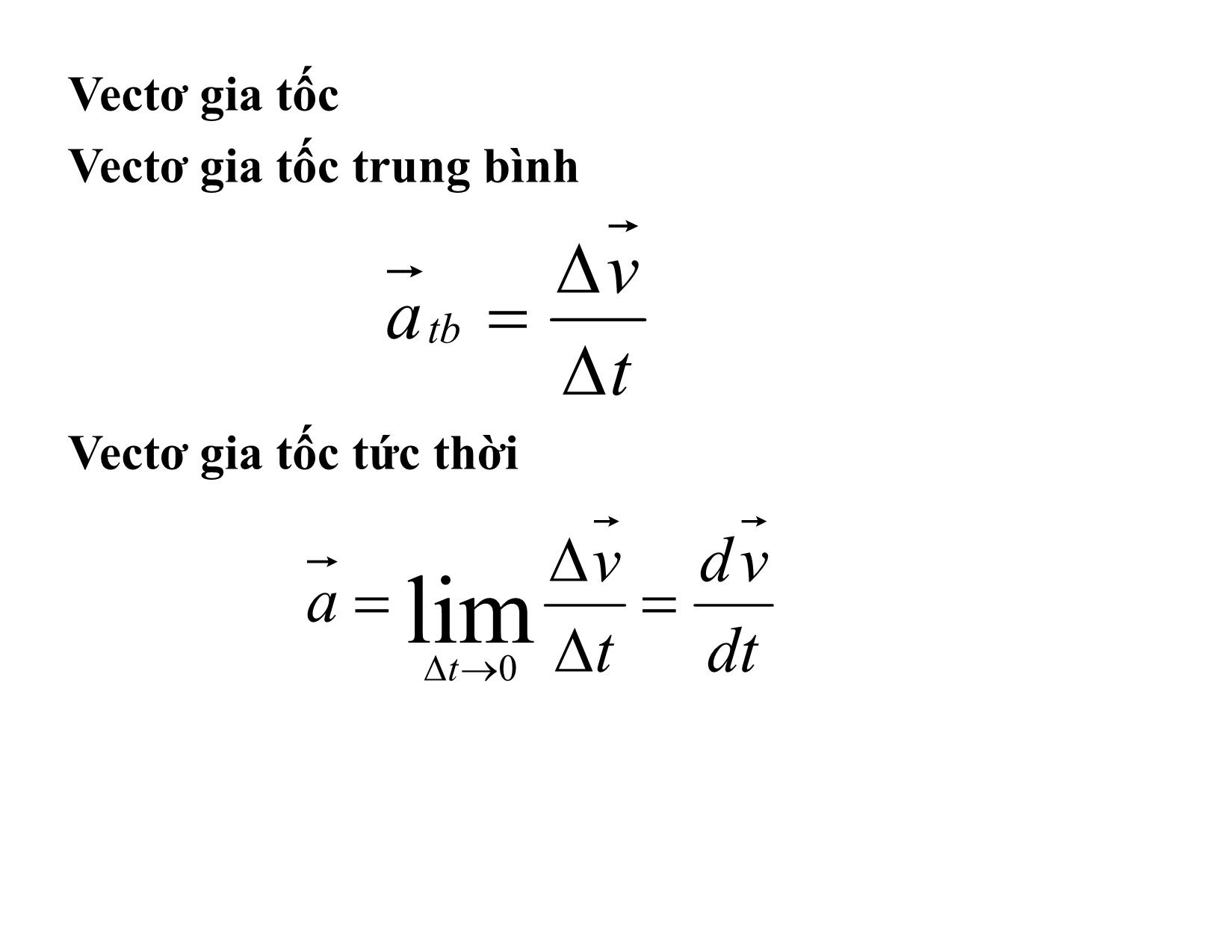
Trang 10
Tải về để xem bản đầy đủ
Tóm tắt nội dung tài liệu: Bài giảng Vật lý đại cương 1 - Chương 1: Động học chất điểm

Chương I ĐỘNG HỌC CHẤT ĐiỂM I. Những khái niệm mở đầu - Chuyển động của một vật là sư chuyển dời vị trí của vật đó đối với các vật khác trong không gian và theo thời gian - Vật hay hệ vật được qui ước đứng yên khi khảo sát chuyển động của các vật khác gọi là hệ qui chiếu. Chuyển động có tính tương đối phụ thuộc HQC. - Chất điểm là một vật có kích thước nhỏ không đáng kể so với những khoảng cách, những kích thước mà ta đang khảo sát - Một tập hợp chất điểm gọi là hệ chất điểm. Vật rắn được xem là hệ chất điểm phân bố liên tục II.Các phương pháp mô tả chuyển động. Quỹ đạo Để xác định chuyển động của chất điểm, cần xác định vị trí của nó trong hệ quy chiếu đã chọn ở mọi thời điểm. Có 3 phương pháp để xác định vị trí của chất điểm 1.Phương pháp vectơ: Gọi O là điểm gắn cố định với hệ qui chiếu, vị trí của chất điểm M được xác định bởi bán kính vectơ r OM M O 2. Phương pháp tọa độ: z Gắn vào điểm gốc O của bán kính M vectơ điểm gốc của một hệ trục tọa O độ Descartes Oxyz với các véctơ y đơn vị trên các trục Ox, Oy, Oz lầnx lượt là i, j,k thì: r xi yj zk Nên vị trí của M được xác định nhờ ba tọa độ x,y,z . Phương trình quỹ đạo Khi chất điểm chuyển động, r (t) cũng như các tọa độ x,y, z của nó thay đổi theo thời gian t: x f (t) M y g(t) z h(t) các phương trình này gọi là phương trình chuyển động của chất điểm trong hệ tọa độ Descartes, khử tham số thời gian t ra khỏi các phương trình này ta sẽ được phương trình quỹ đạo dưới dạng thông thường, tức là dưới dạng hệ thức giữa các toa độ của chất điểm. f (x, y, z) = 0 3. Phương pháp tự nhiên: Ta lấy trên quỹ đạo một điểm cố định O làm gốc và xem quỹ đạo như một trục tọa độ cong rồi quy ước cho nó một chiều dương giống như đối với trục tọa độ thông thường. Khi đó vị trí của điểm M trên quỹ đạo được xác định một cách duy nhất bởi tọa độ cong s bằng khoảng cách từ điểm O tới điểm M theo cung quỹ đạo và mang dấu tương ứng. s = f (t) (1) Phương trình (1) chính là phương trình biểu diển quy luật chuyển động của chất điểm M trên quỹ đạo III. Vectơ vận tốc 1. Vectơ vận tốc trung bình r vtb t 2. Vectơ vận tốc tức thời r d r v lim t 0 t dt Trong hệ t ọa độ De scart es r(t) xi yj zk dr dx dy dz v i j k dt dt dt dt vx i vy j vz k dx dy dz v ; v ; v x dt y dt z dt Trong hệ tọa đ ộ tự nhiên: v v v là độ lớn của vectơ vận tốc là vectơ đơn vị tiếp tuyến với quỹ đạo, có chiều là chiều chuyển động của chất điểm. Vectơ vận tốc đặc trưng cho phương chiều và độ nhanh chậm của chuyển động. v v Vectơ gia tốc Vectơ gia tốc trung bình v atb t Vectơ gia tốc tức thời v dv a lim t 0 t dt Trong hệ tọa độ Descartes dv dv dv dv a x i y j z k a i a j a k dt dt dt dt x y z dv d2x a x x dt dt2 dv d2 y a y y dt dt2 dv d2z a z z dt dt2 2. Gia tốc tiếp tuyến, pháp tuyến: dv dv d a v dt dt dt d d ds d v v . v2 dt ds dt ds τ τ Q Q’ ds dθ dτ τ’ R dθ τ’ O Hình a Xét trường hợp giới hạn khi điểm Q’ trượt trên quỹ đạo tiến đến điểm Q. Khi đó dây cung QQ’ tiến đến trùng với cung tròn QQ’ = ds của đường tròn mật tiếp với quỹ đạo chất điểm tại điểm Q. Gọi R là bán kính của vòng tròn mật tiếp. Từ hình a ta có: ds = dθ/R Mặt khác khi đó dτ sẽ tiến tới vuông góc với τ tại Q. Gọi n là vecto đơn vị vuông góc với tiếp tuyến của quỹ đạo tại Q hướng về tâm O của đường tròn mật tiếp nên: d d n d n d n d d 1 n n d ds R dv v2 Vậy: a n a a dt R t n 2 2 a at an Từ dv v2 (v)2 2v 2v.a dt Như vậy nếu: * v . a 0 Chất điểm chuyển động nhanh dần. * v . a 0 Chất điểm chuyển động chậm dần. * v . a 0 Chất điểm chuyển động tròn đều. a t v a n a a an v a t a a a v v v C Đ N D C Đ C D C Đ tròn đều gọi là gia tốc tiếp tuyến đặc trưng cho sự thay at đổi độ lớn của vectơ vận tốc * Có phương tiếp tuyến với quỹ đạo * Cùng chiều với nếu chuyển đông nhanh dần, ngược chiều với nếu chuyển động chậm dần dv * Có giá trị a (đạo hàm độ lớn của v ) t dt an gọi là gia tốc pháp tuyến đặc trưng cho sự thay đổi phương của vectơ vận tốc * Có phương thẳng góc với tiếp tuyến quỹ đạo * Có chiều hướng về phía lõm của quỹ đạo v2 *Độ lớn a ,R là bán kính của đường tròn n R tiếp xúc với quỹ đạo tại điểm xét đặc trưng cho sự thay đổi của gọi a at an v là vectơ gia tốc toàn phần V. Vận tốc góc, gia tốc góc. 1. Vectơ vận tốc góc được định nghĩa: * Có phương nằm trên trục quay * Có chiều là chiều tiến của nút chai khi xoay nó theo chiều quay của chất điểm. d * Có giá trị dt 2. Vectơ gia tốc góc được định nghĩa: * Có phương nằm trên trục quay * Cùng chiều nếu chuyển động nhanh dần, ngược chiều nếu chuyển động chậm dần d * Có giá trị dt a ω β ω R v R v r r ω R v β r VI. Liên hệ giữa vận tốc và gia tốc thẳng với vận tốc và gia tốc góc. 1. v r v R 2 2 v R 2 2. a R n R R 3. at r at R VII. Phép biến đổi vận tốc và gia tốc. Xét hai hệ qui chiếu K và K’, K ’ chuyển động tịnh tiến đối với K với vận tốc vo Theo phép cộng vectơ ta có: r r' ro r dr dr' dr v r’ dt dt dt ro v v' vo dv dv' dv a o dt dt dt a a' ao VIII. Một số dạng chuyển động cơ đặc biệt 1.Chuyển động thẳng: Khi quỹ đạo là đường thẳng an = 0 ==> a = at a) Chuyển động thẳng đều at = 0 ==> v = const ds v ds vdt dt s t ds vdt so 0 s vt so b) Chuyển động thẳng biến đổi đều a = at = const dv a = a = t dt v t dv adt vo o v vo at v at vo ds at v dt o s t ds at vo dt so o 1 s s at2 v t o 2 o 1 s at2 v t s 2 o o Hệ thức cần nhớ dv dv ds dv a a v t dt ds dt ds v s vdv ads vo so 2 2 v vo 2a s so * Chú ý : Nếu chuyển động thay đổi đều nhưng quỹ đạo không phải là đường thẳng thì phải thay a bằng at 2. Chuyển động tròn: Khi quỹ đạo là đường tròn a) Chuyển động tròn đều: const d t d dt dt o o t o b) Chuyển động tròn thay đổi đều const d t d d t d t o o o t t o d t t d ( t ) d t o o d t 0 0 1 t 2 t 2 o o 2 2 Hệ thức cần nhớ: o 2( o ) 3. Chuyển động parabol Khảo sát chuyển động của một chất điểm xuất phát từ điểm O trong trọng trường với vận tốc ban đầu hợp với mặt phẳng nằm ngang góc α. Giả sử gia tốc trọng trường coi như không đổi. Giải a) Quỹ đạo Chọn mặt ph ẳng hình vẽ là mặt phẳng thẳng đứng chứa v o ; đó cũng là mặt phẳng chứa quỹ đạo của chất điểm,hai trục tọa độ là Ox nằm ngang, Oy thẳng đứng hướng lên. d v g a d v gdt dt v t d v gdt v 0 o v v gt o v gt v o d r gt v o dt r t d r gt v dt 0 0 o 1 2 r gt v ot 2 Chiếu r xuống hai trục Ox, Oy ta được: x x (v0 cos ).t t v0 cos 1 y gt2 (v sin ).t 2 0 g y x2 xtg 2 2 2v0 cos Vậy quỹ đạo của chất điểm là parabol có bề lõm quay xuống b) Tầm xa L 1 L = x khi y = 0 t gt v0 sin 0 2 Vì t > 0 nên : 2v sin t o g 2v 2 sin . cos v 2 sin 2 L 0 0 g g 0 Vậy Lmax khi α = 45 c) Độ cao cực đại: Độ cao cực đạ i là đỉnh S của parabol. Tại đỉnh của parabol v nằm ngang nên vy = 0 v sin v gt v sin 0 t 0 y 0 g 2 1 vo sin vo sin hmax g vo sin . 2 g g v2 sin2 h 0 max 2g d) Bán kính cong v2 v2 an R R an * Tại gốc: v2 v v ;a g.cos R 0 0 n g cos * Tại đỉnh: v2 cos2 v v v cos ;a g R 0 x 0 n g y v hmax g vo x O α an L a t g IX. Đơn vị và thứ nguyên của các đại lượng vật lý 1. Đơn vị vật lý: Muốn định nghĩa đơn vị của tất cả các đại lượng vật lý người ta chỉ cần chọn trước một số đơn vị gọi là đơn vị cơ bản , các đơn vị khác suy ra được từ các đơn vị cơ bản gọi là đơn vị dẫn xuất . Đơn vị cơ bản : Hệ SI - Độ dài mét (m) - Khối lượng kilogam (kg) - Thời gian giây (s) 2. Thứ nguyên: Thứ nguyên của một đại lượng là quy luật nêu lên sự phụ thuộc của đơn vị đo đại lượng đo vào các đơn vị cơ bản. Ví dụ: thể tích của hình hộp chữ nhật, hình trụ thẳng, hình cầu lần lượt là: V = abc ; V = πR2h ; V = 4/3πR3 nếu không để ý đến các hệ số, ta thấy trong mọi trường hợp thể tích = độ dài x độ dài x độ dài , ta nói thứ nguyên của thể tích là (độ dài)3 ký hiệu: thetich do dai3 • Để cho cách viết đơn giản kí hiệu: do dài L thoi gian T khoiluong M Vậy vantoc LT 1 giatoc LT 2 Bài 1: Một chất điểm chuyển động trên mặt phẳng xOy với vận tốc v 2 i x j . Lúc t = 0 chất điểm ở gốc tọa độ O. a) Tìm quỹ đạo của chất điểm. b) Bán kính cong của quỹ đạo tại thời điểm t = 1s a) Ta có: dx x t v 2 dx 2dt x 2t x dt 0 0 dy y t v x 2t dy 2tdt y dt 0 0 x2 y t 2 4 • Vậy quỹ đạo của chất điểm là đường parabol • b) vx 2 ax 0 ;vy x 2t ay 2 a ay 2 2 2 2 v vx vy 4 4t dv 2t at dt 1 t 2 4 a2 a2 a2 n t 1 t 2 v2 3 R 2(1 t 2 ) 2 4 2 an • Bài 2: Hai hạt chuyển động trong trọng trường đều với gia tốc g. Ban đầu hai hạt ở cùng một điểm và có các vận tốc v01= 3m/s, v02 = 4m/s đều nằm ngang theo hai chiều ngược nhau. Xác định khoảng cách giữa hai hạt tại thời điểm các vectơ vận tốc của chúng vuông góc nhau Ta có: v1 gt vo1; O v v20 10 v2 gt vo2 r r 1 2 1 r gt2 v t; 1 2 o1 1 r gt2 v t 2 2 o2 Khoảng cách giữa 2 hạt tại thời điểm t d r1 r2 v01 v02 t Tại thời điểm 2 hạt vuông góc nhau v1.v2 0 gt vo1 gt vo 2 0 2 2 vo1vo 2 g t v .v 0 t o1 o 2 g v v d (v v ) 01 o 2 2,5m o1 o 2 g Bài 3: Một bánh xe quay chậm dần đều, sau một phút vận tốc của nó giảm từ 300vòng/phút xuống 180vòng/phút. Tìm gia tốc góc của bánh xe và số vòng mà bánh xe đã quay được trong một phút ấy. • a) t 0 0 t vòng rad 300 10 ; 0 phút s vòng rad 100 6 phút s 6 10 rad 60 15 s2 1 t2 t 2 0 1 602 10 .60 2 15 480 (rad) Số vòng bánh xe quay được trong 1 phút N 240(vòng) 2 Bài 4: Thả rơi tự do một vật từ độ cao 19,6m.Tìm: a) Quãng đường mà vật rơi được trong 0,1s đầu và 0,1s cuối của thời gian rơi. b) Thời gian cần thiết để vật đi hết 1m đầu và 1m cuối của độ cao h Chọn gốc tọa độ là vị trí thả vật, gốc thời gian là lúc thả vật, chiều dương hướng xuống. Ta có 1 y gt 2 2 a) Quãng đường vật rơi được trong 0,1s đầu tiên 1 là: h .9,8.0,12 0,049m 1 2 Thời gian để vật rơi hết quãng đường h là: 2h 2.19,6 t 2s g 9,8 Quãng đường vật rơi trong khoảng thời gian 0,1s cuối của thời gian rơi: 1 h h g (t 0,1) 2 19, 6 4, 9.(1, 99) 2 1, 9m 2 2 b) Thời gian vật rơi 1m đầu 2y 2 t 0,45s g 9,8 Thời gian để vật rơi 18,6m 2y 2.18,6 t 1,95s g 9,8 Thời gian để vật rơi 1m cuối: t = 2 - 1,95 = 0,05 s Bài 5: Một h ạt r ời gốc tọa độ với vận tốc đầu v o 3 i m/s và gia tốc a i 0,5 j m / s2 . Tìm vận tốc của hạt khi nó đạt tọa độ x lớn nhất. • Ta có: dv v t a dv adt dt v 0 0 v at v0 (3 t)i 0,5 j xmax khi : dx 0 v 0 t 3 dt x v 1,5 j • Bài 6: Một hòn đá được ném theo phương nằm ngang với vận tốc vo = 15m/s. Tính gia tốc tiếp tuyến và gia tốc pháp tuyến sau lúc ném 1s. Ta có: v o 2 2 2 v gt v0 v g t v0 g dv g 2t a 5,36m / s2 t dt 2 2 2 g t v0 2 2 2 2 2 an a at g at 8,20m / s • Bài 7: Một chất điểm đang quay xung quanh một trục cố định với gia tốc góc β =bt, trong đó b =2.10-2 rad/s3. Hỏi trong khoảng thời gia bao lâu kể từ lúc bắt đầu chuyển động, vectơ gia tốc toàn phần của 0 chất điểm làm một góc θ0 = 60 với vectơ vận tốc của nó. Ta có: 2 a a R ;a R n t n at a 2 O v tg n ; a at d t 1 bt d btdt bt2 dt 0 0 2 1 3 bt tg 3 tg t 4 7s 4 b • Bài 8: Một người đứng dưới đất thấy hạt mưa rơi thẳng đứng, với tốc độ 10m/s. Hỏi người lái xe trên đường ngang với tốc độ 1 0 3 m / s sẽ thấy hạt mưa rơi với tốc độ v, lệch khỏi phương thẳng đứng góc bằng bao nhiêu? Gọi v là vận tốc hạt mưa đối với đất 1 v là vận tốc của xe đối với đất 2 v12 là vận tốc hạt mưa đối với xe Ta có: v 2 v1 v12 v2 α v12 v1 2 2 v12 v1 v2 20m / s v tg 2 3 60o v1 Một chiếc thuyền bơi từ bến A đến B ở cùng một bên bờ sông, với vận tốc so với nước là v1 = 3 km/h. Cùng lúc ấy một cano chạy từ bến B theo hướng đến bến A với vận tốc đối với nước là v2 = 10 km/h. Trong thời gian thuyền đi từ A đến B thì cano kịp đi được 4 lần khoảng cách đó và về đến B cùng lúc với thuyền. Xác định hướng và tốc độ của nước sông Giả sử nước sông chảy từ A đến B và gọi khoảng cách AB là s, vận tốc của dòng nước là vo . Theo đầu bài ta có: s s s 2 v1 vo v2 vo v2 vo 2 vo 40vo 20 0 vo 39,5km / h; vo 0,5km / h; Loại nghiệm vo = -39,5km/h. Vậy vo = -0,5 km/h. Dấu trừ chứng tỏ dòng nước chảy từ B đến A.
File đính kèm:
 bai_giang_vat_ly_dai_cuong_chuong_1_dong_hoc_chat_diem.pdf
bai_giang_vat_ly_dai_cuong_chuong_1_dong_hoc_chat_diem.pdf

