Bài giảng Toán tổ hợp - Chương 6: Các bài toán về đường đi

CÁC BÀI TOÁN VỀ ĐƯỜNG ĐI 
Chương 6 
2 
1. Tìm đường đi ngắn nhất 
2. Đồ thị Euler 
3. Đồ thị Hamilton 
Nội dung 
3 
1. TÌM ĐƯỜNG ĐI NGẮN 
NHẤT 
4 
Định nghĩa. Cho G = (V,E) là đồ thị có trọng số. Với 
H G thì trọng lượng của H là tổng trọng lượng của 
các cạnh của H. 
 Nếu H là đường đi, chu trình, mạch thì w(H) được 
gọi là độ dài của H. 
 Nếu mạch H có độ dài âm thì H được gọi là mạch 
âm. 
 Khoảng cách giữa 2 đỉnh u và v là độ dài ngắn 
nhất của các đường đi từ u đến v. 
(H) ( )
e H
w w e
 
Định nghĩa 
5 
Định nghĩa. Cho đồ thị G = (V, E), V = {v1,v2,,vn} 
có trọng số. Ma trận khoảng cách của G là ma 
trận D= (dij) xác định như sau: 
0
( )ij i j i j
i j
khi i j
d w v v khi v v E
khi v v E
Nhận xét. Mọi đồ thị được hoàn toàn xác định bởi 
ma trận khoảng cách. 
Ma trận khoảng cách 
6 
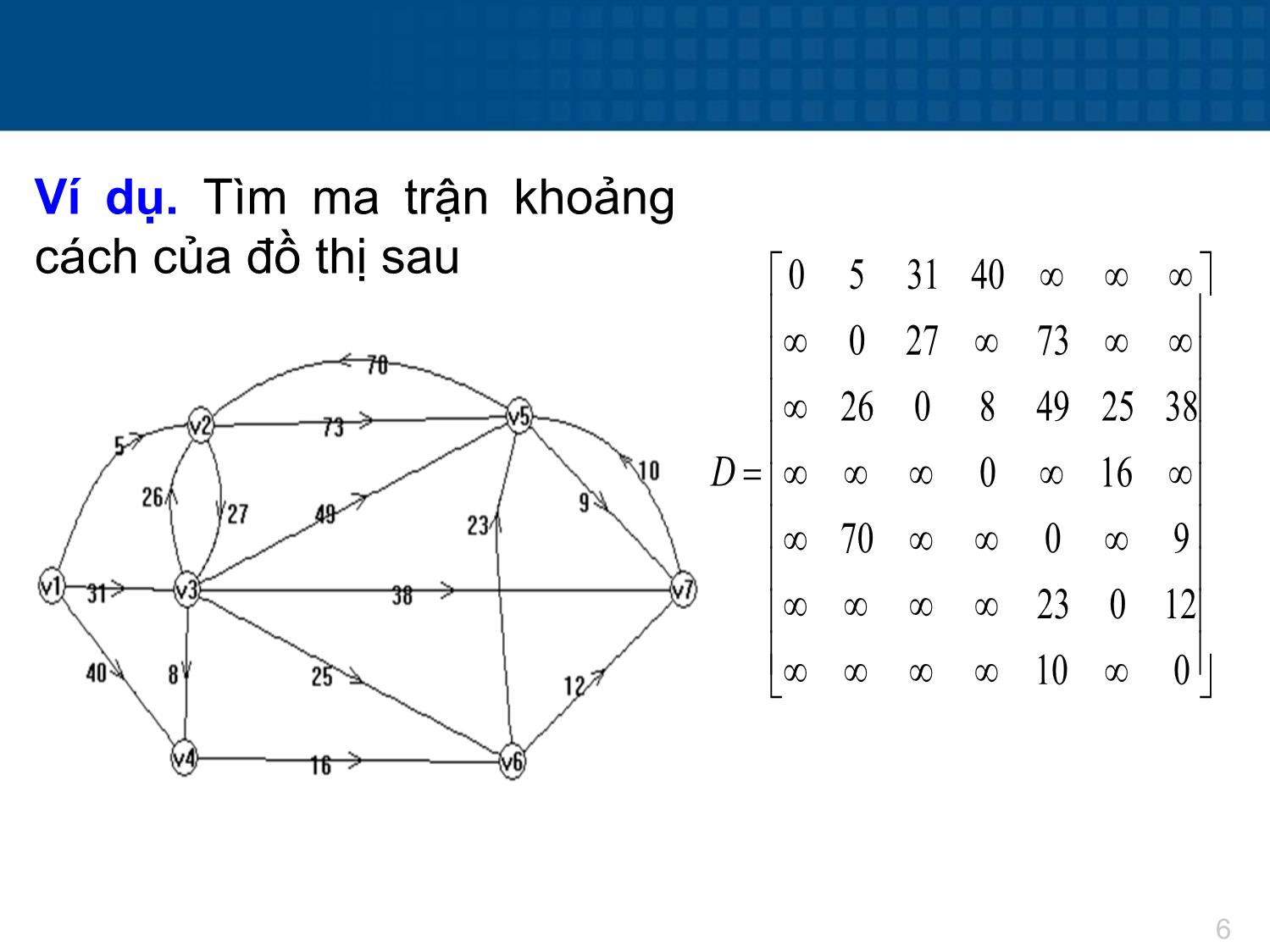
0 5 31 40
0 27 73
26 0 8 49 25 38
0 16
70 0 9
23 0 12
10 0
D
Ví dụ. Tìm ma trận khoảng 
cách của đồ thị sau 
7 
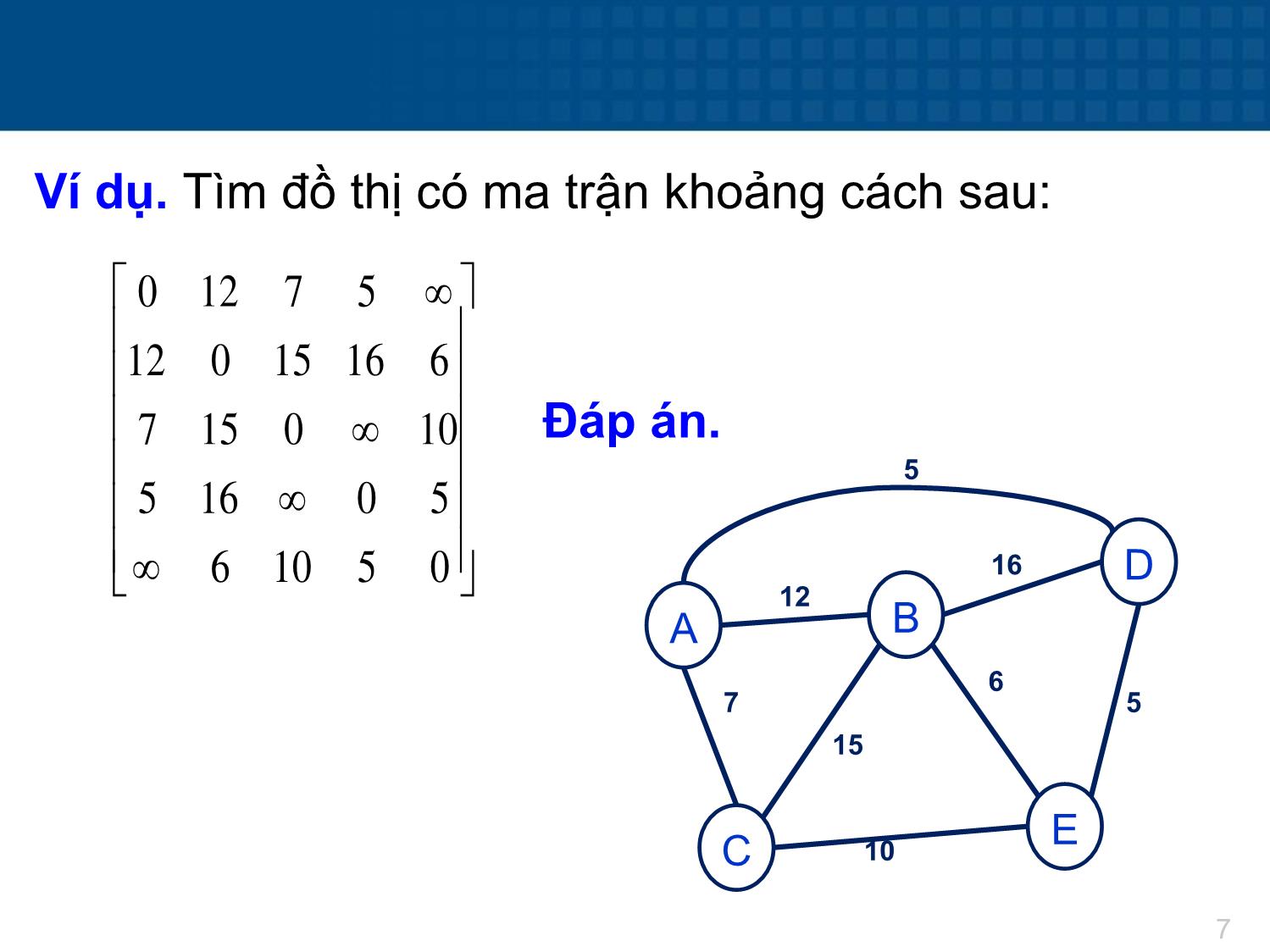
Ví dụ. Tìm đồ thị có ma trận khoảng cách sau: 
0 12 7 5
12 0 15 16 6
7 15 0 10
5 16 0 5
6 10 5 0
Đáp án. 
C 
A B 
D 
E 
12 
7 
15 
6 
5 
5 
10 
16 
8 
Bài toán. Cho G = (V, E) là đồ thị có trọng số. Tìm 
đường đi ngắn nhất từ u đến v và tính khoảng cách 
d(u ,v). 
Nhận xét. Nếu đồ thị G có mạch âm  trên một 
đường đi từ u tới v thì đường đi ngắn nhất từ u đến v 
sẽ không tồn tại. 
u v 
 
9 
Khi tìm đường đi ngắn nhất ta có thể bỏ bớt đi các 
cạnh song song và chỉ để lại một cạnh có trọng 
lượng nhỏ nhất. 
Đối với các khuyên có trọng lượng không âm thì 
cũng có thể bỏ đi mà không làm ảnh hưởng đến kết 
quả của bài toán. 
Đối với các khuyên có trọng lượng âm thì có thể 
đưa đến bài toán tìm đường đi ngắn nhất không có 
lời giải. 
Một số lưu ý 
10 
Gọi P là đường đi ngắn nhất từ đỉnh u đến đỉnh v; t 
P. Giả sử P=P1P2 với P1 là đường đi con của P từ u 
đến t và P2 là đường đi con của P từ t đến v. Khi đó 
P1 cũng là đường đi ngắn nhất từ u đến t. 
w(P1’) < w(P1) w(P1’P2) < w(P1P2)=w(P) 
u v 
t 
P1 
P1
’ 
P2 
Nguyên lý Bellman 
Chứng minh. Giả sử tồn tại P1
’ là đường đi ngắn hơn 
P1
 ta có 
Vô lý vì P là đường đi ngắn nhất từ u đến v 
11 
Để tìm đường đi ngắn nhất, chúng ta quan tâm tới 
hai thuật toán: 
 Thuật toán Dijkstra không thể thực hiện khi đồ thị 
có cạnh âm 
 Thuật toán Ford – Bellman xác định các mạch 
(chu trình) âm hay trả về cây đường đi ngắn nhất 
Thuật toán tìm đường đi ngắn nhất 
12 
Thuật toán Dijkstra 
Xác định tuần tự các đỉnh có khoảng cách đến u0 từ nhỏ 
đến lớn. 
 Trước tiên đỉnh có khoảng cách nhỏ nhất đến u0 là u0. 
 Trong V\{u0} tìm đỉnh có khoảng cách đến u0 nhỏ nhất 
(đỉnh này phải là một trong các đỉnh kề với u0) giả sử 
đó là u1 
 Trong V\{u0,u1} tìm đỉnh có khoảng cách đến u0 nhỏ 
nhất (đỉnh này phải là một trong các đỉnh kề với u0 
hoặc u1) giả sử đó là u2
13 
Tiếp tục như trên cho đến bao giờ tìm được khoảng 
cách từ u0 đến mọi đỉnh. 
Nếu G có n đỉnh thì: 
 0 = d(u0,u0) < d(u0,u1) d(u0,u2)  d(u0,un-1) 
14 
Bước 1. i:=0, S:=V\{u0}, L(u0):=0, L(v):= với mọi v S 
và đánh dấu đỉnh v bởi ( ,-). Nếu n=1 thì dừng và xuất 
d(u0,u0)=0=L(u0) 
Bước 2. Với mọi v S và kề với ui (nếu đồ thị có hướng 
thì v là đỉnh sau của ui), đặt 
 L(v):= min{ L(v), L(ui)+w(ui v)}. 
Xác định k= min L(v) , v S. 
Nếu k= L(vj) thì xuất d(u0,vj )= k và đánh dấu đỉnh vj bởi 
(k; ui). Đặt ui+1:= vj và S:=S\{ui+1} 
Bước 3. i:=i+1. Nếu i = n-1 thì kết thúc. 
Nếu không thì quay lại Bước 2 
Thuật toán Dijkstra 
15 
Bài tập 1. Tìm đường đi ngắn nhất từ u đến các đỉnh 
còn lại. 
7 
1 
3 
5 3 
1 
2 
3 
3 
1 
4 
u 
r 
s 
x 
w 
z y 
t 
4 
Một số ví dụ 
u r s t x y z w 
0* ( ,-) ( ,-) ( ,-) ( ,-) ( ,-) ( ,-) ( ,-) 
- (4,u0) ( ,-) ( ,-) ( ,-) (1,u0)* ( ,-) ( ,-) 
- (3,y)* ( ,-) ( ,-) ( ,-) - (4,y) ( ,-) 
7 
1 
3 
5 3 
1 
2 
3 
3 
1 
4 
u 
r 
s 
x 
w 
z 
y 
t 
4 
7 
1 
3 
5 3 
1 
2 
3 3 
1 
4 
u 
r s 
x 
w z y 
t 
4 
u r s t x y z w 
0* ( ,-) ( ,-) ( ,-) ( ,-) ( ,-) ( ,-) ( ,-) 
- (4,u0) ( ,-) ( ,-) ( ,-) (1u0)* ( ,-) ( ,-) 
- (3,y)* ( ,-) ( ,-) ( ,-) - (4,y) ( ,-) 
- - (10,r) (6,r) ( ,-) - (4,y)* ( ,-) 
- - (10,r) (6,r)* ( ,-) - - (9,z) 
- - (9,t) - (7,t)* - - (9,z) 
- - (8,x)* - - - - (9,z) 
- - - - - - - (9,z)* 
18 
Cây đường đi 
u 
y z 
w 
r 
t x 
s 
1 
2 
3 
1 
1 
3 5 
Ví dụ. Cho đồ thị có trọng số G = (V, E), V = { v1, v2, v3, 
v4, v5, v6, v7} xác định bởi ma trận trọng số D. Dùng 
thuật toán Dijkstra tìm đường đi ngắn nhất từ v1 đến 
các đỉnh v2, v3, v4, v5, v6, v7 
0 5 31 40
0 27 73
26 0 8 49 25 38
0 16
70 0 9
23 0 12
10 0
D
20 
21 
v1 v2 v3 v4 v5 v6 v7 
0* ( ,-) ( ,-) ( ,-) ( ,-) ( ,-) ( ,-) 
- (5,v1)* (31,v1) (40,v1) ( ,-) ( ,-) ( ,-) 
- - (31,v1)* (40,v1) (78,v2) ( ,-) ( ,-) 
- - - (39,v3)* (78,v2) (56,v3) (69,v3) 
- - - - (78,v2) (55,v4)* (69,v3) 
- - - - (78,v2) - (67,v6)* 
- - - - (77,v7) - - 
22 
Cây đường đi 
23 
Ví dụ. Dùng thuật toán Dijsktra để